平面几何真题汇编
2016-2020 北京中考几何真题汇编
1 如图,点 \(A,B,C\) 在同一条线上,点 \(B\) 在点 \(A,C\) 之间,点 \(D,E\) 在直线 \(AC\) 同侧, \(AB<BC\) ,\(\angle{A}=\angle{C}=90^\circ\) ,\(\triangle{EAB}\cong\triangle{BCD}\) ,连接 \(DE\) ,设 \(AB=a,BC=b,DE=c\) ,给出下面三个结论:\((1)a+b<c, (2)a+b>\sqrt{a^2+b^2}, (3)\sqrt{2}(a+b)>c\) ;
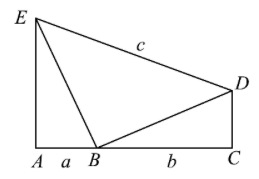
上述结论中,所有正确结论的序号是:
A. \((1),(2)\) \(\qquad\) B. \((1)(3)\) \(\qquad\) C. \((2)(3)\) \(\qquad\) D. \((1)(2)(3)\)
2 如图,直线 \(AD,BC\) 交于点 \(O\) ,

6 如图 5 所示,菱形 \(ABCD\) 的对角线 \(AC,\ BD\) 相交于点 \(O,\ E\) 是 \(AD\) 的中点,点 \(F,\ G\) 在 \(AB\) 上, \(EF\perp AB,\ OG \parallel EF\) 。
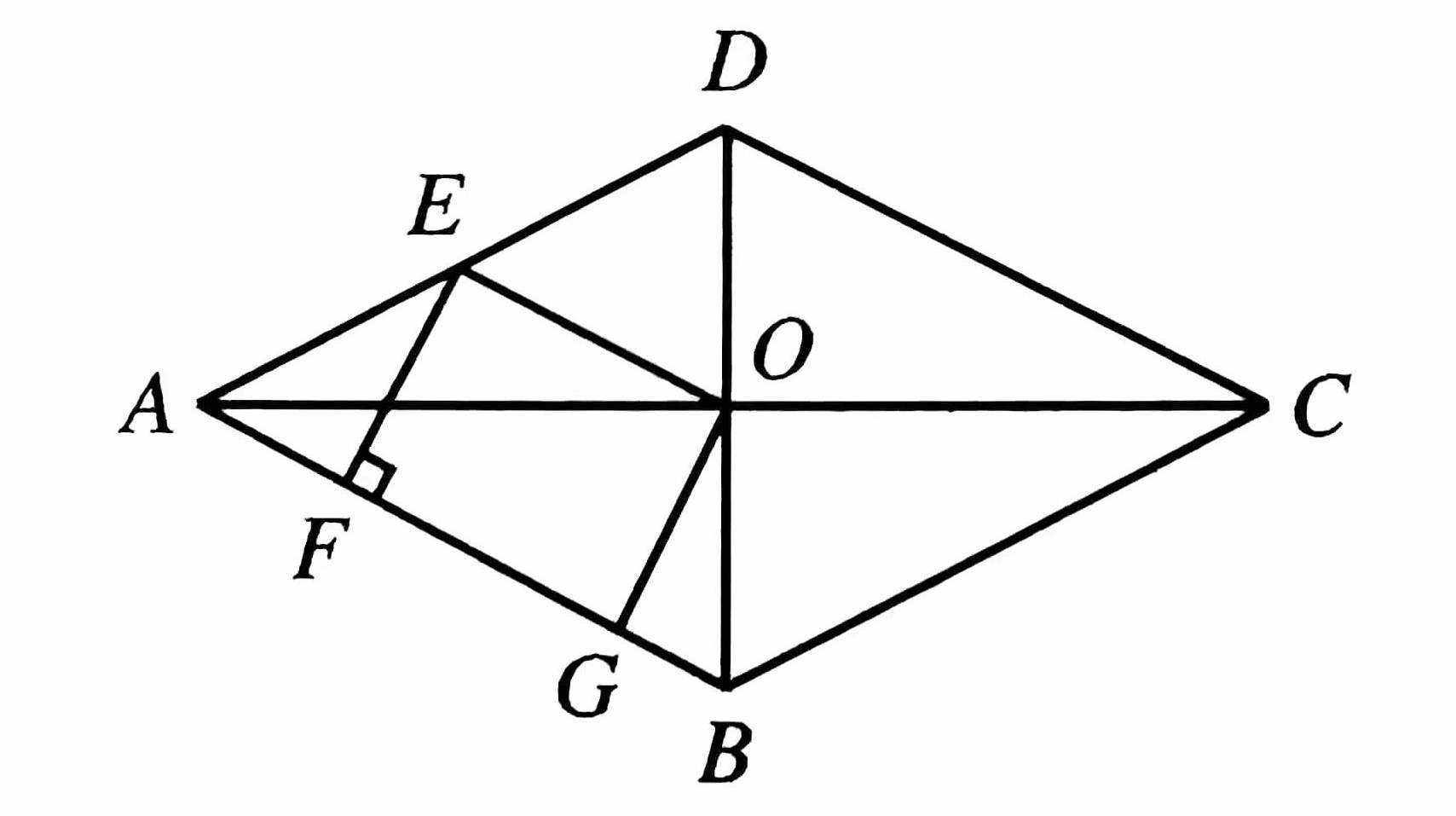
- [(1)] 求证:四边形 \(OEFG\) 是矩形;
- [(2)] 若 \(AD=10,\ EF=4\) ,求 \(OE\) 和 \(BG\) 的长。
7 如图 6 所示, \(AB\) 是 \(\bigodot O\) 的直径, \(C\) 为 \(BA\) 延长线上一点, \(CD\) 是 \(\bigodot O\) 的切线, \(D\) 为切点, \(OF\perp AD\) 于点 \(E\) ,交 \(CD\) 于点 \(F\) 。

- [(1)] 求证:\(\angle{ADC}=\angle{AOF}\) ;
- [(2)] 若 \(\sin C=\dfrac{1}{3},\ BD=8\) ,求 \(EF\) 的长。
8 如图 7 所示,在 \(\triangle{ABC}\) 中, \(\angle{C}=90^\circ\) , \(AC>BC\) , \(D\) 是 \(AB\) 的中点。 \(E\) 为直线 \(AC\) 上一动点,连接 \(DE\) ,过点 \(D\) 作 \(DF\perp DE\) ,交直线 \(BC\) 于点 \(F\) ,连接 \(EF\) 。
- [(1)] 如图 1 ,当 \(E\) 是线段 \(AC\) 的中点时,设 \(AE=a,\ BF=b\) ,求 \(EF\) 的长(用含 \(a,b\) 的式子表示);
- [(2)] 当点 \(E\) 在线段 \(CA\) 的延长线上时,依题意补全图 2 ,用等式表示线段 \(AE,\ EF,\ BF\) 之间的数量关系,并证明。
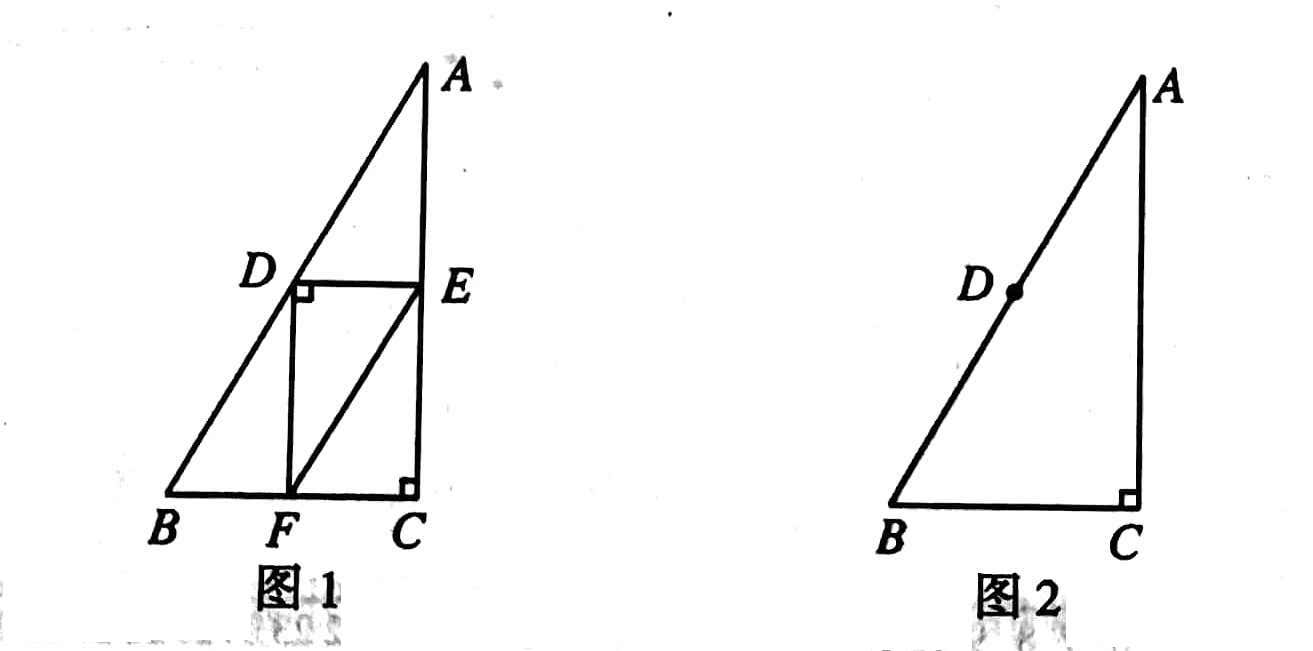
9 在平面直角坐标系中 \(xOy\) 中,\(\bigodot O\) 的半径为 \(1\) , \(A,\ B\) 为 \(\bigodot O\) 外两点, \(AB=1\) 。
给出如下定义:平移线段 \(AB\) ,得到 \(\bigodot O\) 的弦 \(A'B'\) (\(A',B'\) 分别为点 \(A,B\) 的对应点) ,线段 \(AA'\) 长度的最小距离值称为线段 \(AB\) 到 \(\bigodot O\) 的“平移距离”。
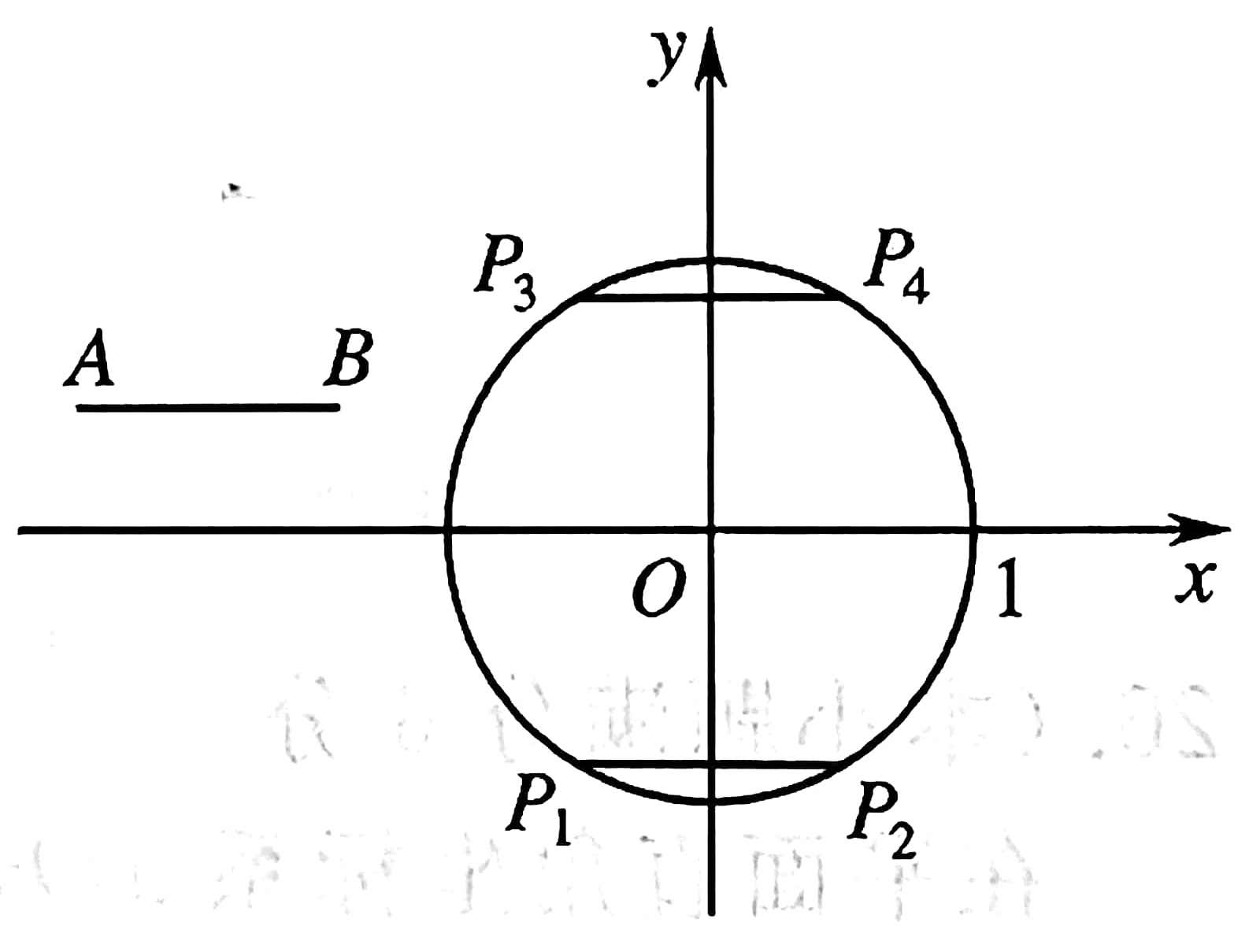
- [(1)] 如图,平移线段 \(AB\) 得到 \(\bigodot O\) 的长度为 \(1\) 的弦 \(P_1P_2\) 和 \(P_3P_4\) 中,则这两条弦的位置关系是 \(\_\_\_\_\_\_\) ;在点 \(P_1,\ P_2,\ P_3,\ P_4\) 中,连接点 \(A\) 与点 \(\_\_\_\_\_\_\) 的线段的长度等于线段 \(AB\) 到 \(\bigodot O\) 的“平移距离”;
- [(2)] 若点 \(A,B\) 都在直线 \(y=\sqrt{3}x+2\sqrt{3}\) 上,即线段 \(AB\) 到 \(\bigodot O\) 的“平移距离”为 \(d_1\) ,求 \(d_1\) 的最小值;
- [(3)] 若点 \(A\) 的坐标为 \(\left(2,\ \dfrac{3}{2}\right)\) ,记线段 \(AB\) 到 \(\bigodot O\) 的“平移距离”为 \(d_2\) ,直接写出 \(d_2\) 的取值范围。
10 如图 9 所示,在菱形 \(ABCD\) 中, \(AC\) 为对角线,点 \(E,F\) 分别在 \(AB,AD\) 上, \(BE=DF\) ,连接 \(EF\) 。

- [(1)] 求证: \(AC\perp EF\) ;
- [(2)] 延长 \(EF\) 交 \(CD\) 的延长线于点 \(G\) ,连接 \(BD\) 交 \(AC\) 于点 \(O\) 。若 \(BD=4\) ,\(\tan G=\dfrac{1}{2}\) ,求 \(AO\) 的长。
11 在平面内,给定不在同一条直线上的点 \(A,B,C\) ,点 \(O\) 到 \(A,B,C\) 的距离均等于 \(a\) ( \(a\) 为常数) ,到点 \(O\) 的距离等于 \(a\) 的所有点组成图形 \(G\) ,\(\angle{ABC}\) 的平分线交图形 \(G\) 于点 \(D\) ,连接 \(AD,CD\) 。
- [(1)] 求证:\(AD=CD\) ;
- [(2)] 过点 \(D\) 做 \(DE\perp BA\) ,垂足为 \(E\) ,做 \(DF\perp BC\) ,垂足为 \(F\) ,延长 \(DF\) 交图形 \(G\) 于点 \(M\) ,连接 \(CM\) 。若 \(AD=CM\) ,求直线 \(DE\) 于图形 \(G\) 的公共点个数。
12 已知 \(\angle{AOB}=30^\circ\) , \(H\) 为射线 \(OA\) 上一定点, \(OH=\sqrt{3}+1\) , \(P\) 为射线 \(OB\) 上一点, \(M\) 为射线 \(OH\) 上一动点,连接 \(PM\) ,满足 \(\angle{OMP}\) 为钝角,以点 \(P\) 为中心,将线段 \(PM\) 顺时针旋转 \(150^\circ\) ,得到线段 \(PN\) ,连接 \(ON\) 。
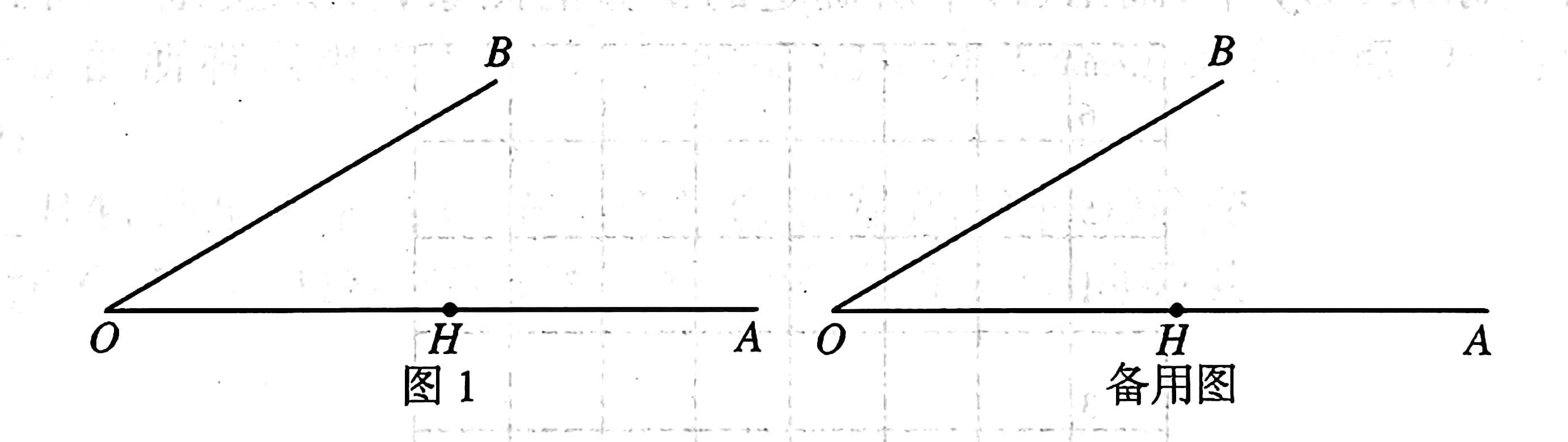
- [(1)] 依题意补全图 1 ;
- [(2)] 求证:\(\angle{OMP}=\angle{OPN}\) ;
- [(3)] 点 \(M\) 关于点 \(H\) 的对称点为 \(Q\) ,连接 \(QP\) 。写出一个 \(OP\) 的值,使得对于任意的点 \(M\) 总有 \(ON=QP\) ,并证明。
13 在 \(\triangle{ABC}\) 中, \(D,E\) 分别是 \(\triangle{ABC}\) 两边的中点,如果 \(\wideparen{DE}\) 上的所有点都在 \(\triangle{ABC}\) 的内部或边上,则称 \(\wideparen{DE}\) 为 \(\triangle{ABC}\) 的一条中内弧。例如,图 1 中 \(\wideparen{DE}\) 是 \(\triangle{ABC}\) 的一条中内弧。
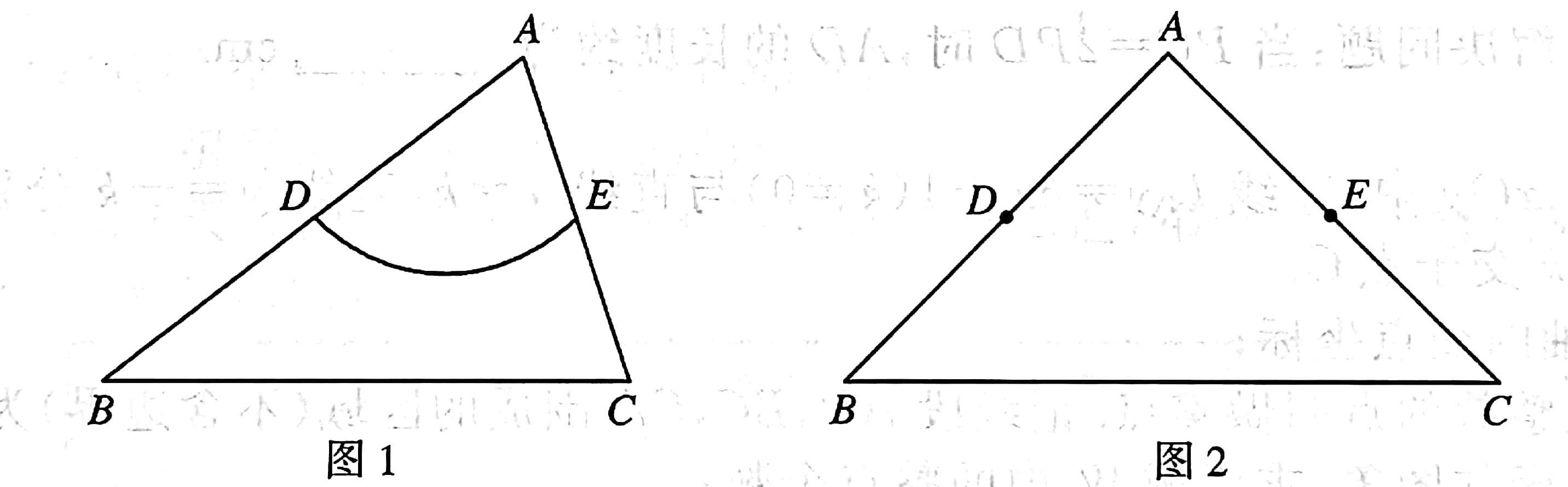
[(1)] 如图 2 ,在 \(Rt\triangle{ABC}\) 中, \(AB=AC=2\sqrt{2}\) , \(D,E\) 分别是 \(AB,AC\) 的中点。画出 \(\triangle{ABC}\) 的最长的中内弧 \(\wideparen{DE}\) ,并直接写出此时 \(\wideparen{DE}\) 的长;
[(2)] 在平面直角坐标系中,已知点 \(A(2,0),\ B(0,0),\ C(4t,0)(t>0)\) 。在 \(\triangle{ABC}\) 中, \(D,E\) 分别是 \(AB,AC\) 的中点。
[] 若 \(t=\dfrac{1}{2}\) ,求 \(\triangle{ABC}\) 的中内弧 \(\wideparen{DE}\) 所在圆的圆心 \(P\) 的纵坐标的取值范围;
[] 若在 \(\triangle{ABC}\) 中存在一条中内弧 \(\wideparen{DE}\) ,使得 \(\wideparen{DE}\) 所在圆的圆心 \(P\) 在 \(\triangle{ABC}\) 的内部或边上,直接写出 \(t\) 的取值范围。
14 如图 12 所示,点 \(A,B,C,D\) 在 \(\bigodot O\) 上, \(\wideparen{CB}=\wideparen{CD}\) ,\(\angle{CAD}=30^\circ\),\(\angle{ACD}=50^\circ\) ,则 \(\angle{ADB}=\_\_\_\_\_\_^\circ\).
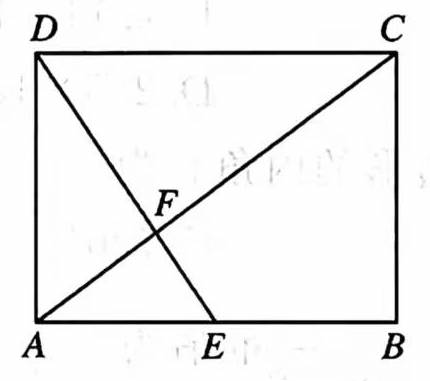
15 如图 13 所示,在矩形 \(ABCD\) 中, \(E\) 是边 \(AB\) 的中点,连接 \(DE\) 交对角线 \(AC\) 于点 \(F\) ,若 \(AB=4,\ AD=3\) ,则 \(CF\) 的长为 $______ $ .