二次函数（英文）

The Concept of Functions

The Definition of Functions

A function is a relation in which each elelment of the domain corresponds with exactly on element of the range.

示例： Identifying Functions

Which relation(s) represent functions?

In relation B, the element ‘2’ coresponds with two elements of the range.

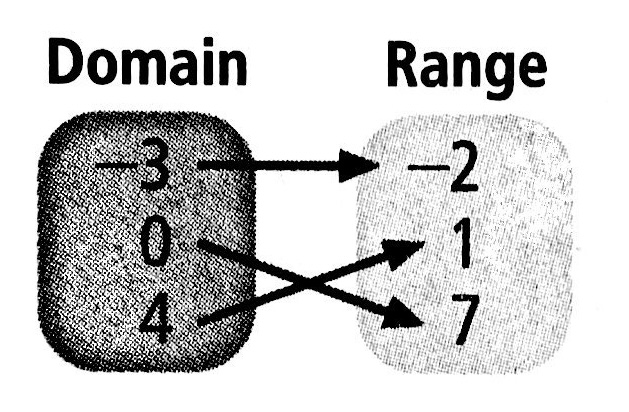\(\qquad\) B.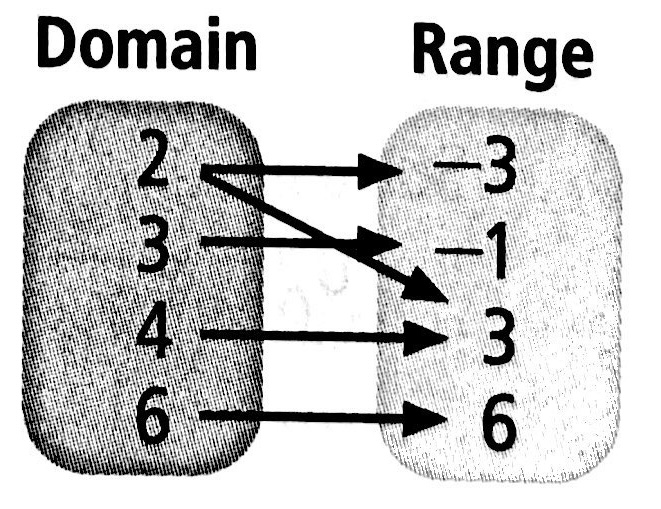

Answer Relation A represents a function.

☐

We represent functions graphically by plotting points on a coordinate plane. The coordinate plane is a grid formed by a horizontal number line and a vertical number line that cross at a point called the origin. The origin has this name because it is the “starting” location; every other point on the grid is described in terms of how far it is from the origin. The horizontal number line is called the x–axis and the vertical line is called the y-−axis. We can represent each value of a function as a point on the plane by representing the x-−value as a distance along the x−-axis and the y-−value as a distance along the y-−axis.

You can use the vertical-line test to determine whether a relation is a function. The vertical-line test states that if a vertical line passes through more than one point on the graph of relation.

示例： Vertical-line Test

Use the Vertical-line test. Which graph(s) represent functions?

Graphs A and C fail the vertical-line test because for each graph, a vertical line passes through than one point.

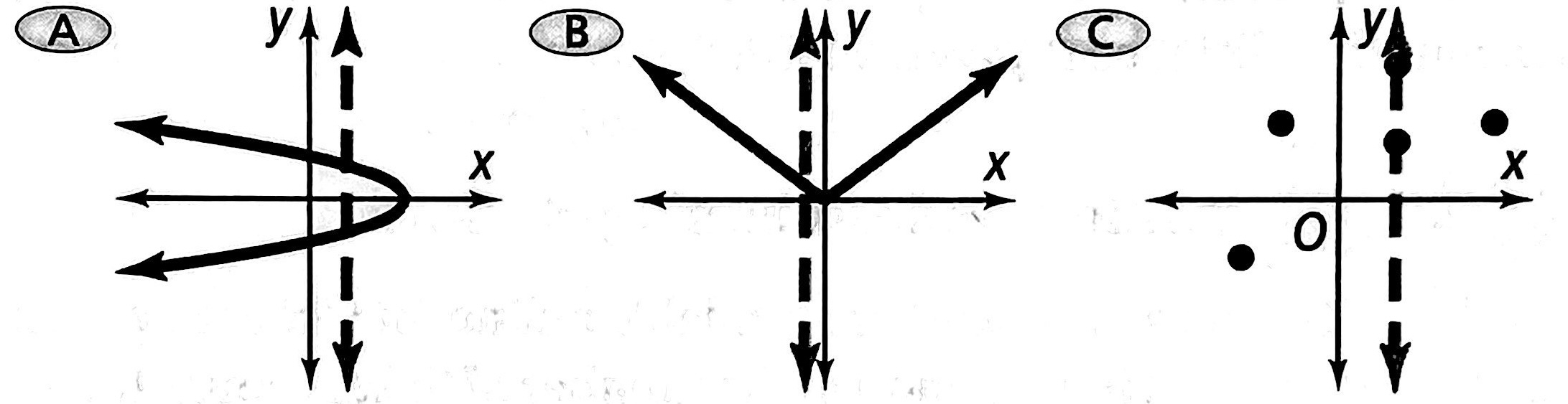
Answer Graph B represents a function.

☐

函数这一概念最早由中国清朝数学家李善兰翻译，出于其著作《代数学》：“凡此变数中函彼变数者，则此为彼之函数”。意思是，函数指一个量随着另一个量的变化而变化，或者说一个量中包含另一个量。这实际上是函数最朴素的定义。

传统定义（人教版初中课本）

定义：在一个变化过程中，发生变化的量叫变量，有些数值是不随变量而改变的，我们称它们为常量。

自变量（x）：一个与它量有关联的变量，这一量中的任何一值都能在它量中找到对应的固定值。

因变量（y）：随着自变量的变化而变化，且自变量取唯一值时，因变量有且只有唯一值与其相对应。

函数关系：上述因变量和自变量之间的关系称为函数关系。 \(x\) 确定一个值，\(y\) 就随之确定一个值。当 \(x\) 取 \(a\) 时， \(y\) 就随之确定为 \(b\)， \(y_1\) 就叫做 \(x_1\) 的函数值。

集合、映射和函数

定义：设 \(X\) 和 \(Y\) 是两个非空集合，如果按照某种对应关系，对于集合 \(X\) 中的任何一个元素，在集合 \(Y\) 中都存在唯一的元素与之对应，那么这样的对应叫做集合 \(A\) 到集合 \(B\) 的映射。定义在非空数集之间的映射称为函数。

如果读者阅读更广泛的数学教材，会发现映射和函数这两个字眼的区分有时不是那么清晰，有些著作以“映射”作为统一名称，有的著作则使用“函数”字眼。

在我国现行中学教材中，映射是在集合间定义的，而函数是在数集（实数集）之间定义的。函数是一种特殊的映射。

Quadratic Functions and Transformations

In , the birds fly along a parabolic path.

Parabola: 抛物线\ Quadratic function: 二次函数\Vertex form: 顶点式\Axis of symmetry: 对称轴

Parabolas and Quadratic Functions

A Parabola is the graph of a quadratic function, which you can write in the form \(f(x)=ax^2+bx+c\), where \(a\neq0\) .

The graph of any quadratic function is a transfromation of the graph of the parent function, \(y=x^2\).

The vertex form of a quadratic function is \[f(x)=a(x-h)^2+k,\ where\ a\neq0\]

The axis of symmetry is a line that divides a parabola into two mirror images. The equation of the axis of the symmetry is \(x=h\). The vertex of the parabolla is \((h,k)\), the intersection of the parabolla and its axis of symmetry.

示例：

Draw the graph of \(y=x^2\).

示例：

Draw the graph of \(y=\dfrac{1}{4}x^2\).

Reflection, Stretch, and Compression

Graphs of \(y=ax^2\) and \(y=-ax^2\) are reflections of each other across the x–axis.

Increasing \(|a|\) stretches the graph vertically and narrows it horizontally.

Decreasing \(|a|\) compresses the graph vertically and widens it horizontally.

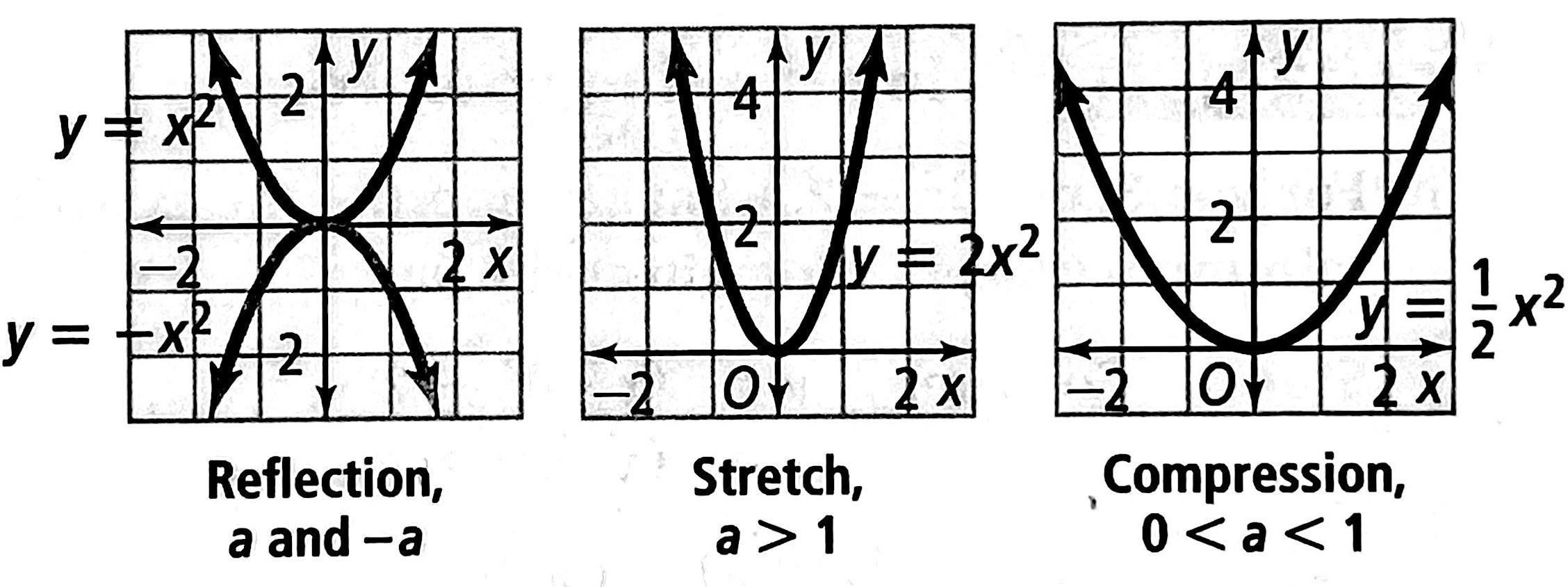
Reflection, Stretch, and Compression of the parent function \(y=x^2\)

Parabolic opening of \(\mathbf{f(x)=ax^2}\)

If \(a>0\), the parabola opens upward. The y–coordinate of the vertex is the minimum value of the function.

If \(a<0\), the parabola opens downward. The y–coordinate of the vertex is the maximum value of the function.

示例：

Graph \(g(x)=x^2-3\). How is it a translation of \(f(x)=x^2\) ?

示例：

Graph \(g(x)=(x-4)^2\). How is it a translation of \(f(x)=x^2\) ?

思考与讨论

How is \(g(x)=x^2+3\) a translation of \(f(x)=x^2\) ?
How is \(g(x)=(x+1)^2\) a translation of \(f(x)=x^2\) ?
For \(f(x)=a(x-h)^2+k\), how do the parameters \(a,h,k\) control the graph of \(f(x)\) ?

示例： Interpreting Vertex Form

For \(y=3(x-4)^2-2\), what are the vertex, the axis of symmetry, the maximum of minimum value, the domain and the range?

Plan: Compare \(y=3(x-4)^2-2\) to vertex form \(y=a(x-h)^2+k\) to find values for \(a\), \(h\), and \(k\).

解：

Step 1 \(\qquad\) Compare: \(\ y=3(x-4)^2-2\)

\(\qquad\qquad\qquad\qquad\qquad\) \(y=a(x-h)^2+k\)

Step 2 \(\qquad\) The vertex is \((h,k)=(4,-2)\).

Step 3 \(\qquad\) The axis of symmetry is \(x=h\), or \(x=4\).

Step 4 \(\qquad\) Since \(a>0\), the parabola opens upward. \(k=-2\) is the minimum value.

Step 5 \(\qquad\) Domain: All real numbers. There is no restriction on the value of \(x\).

\(\qquad\qquad\quad\) Range: All real numbers \(\geq-2\), since the minimum value of \(f(x)\) is \(-2\).

☐

示例： Interpreting Vertex Form

For \(y=-2(x+1)^2+4\), what are the vertex, the axis of symmetry, the maximum of minimum value, the domain and the range?

You can use the vertex form of a quadratic function, \(f(x)=a(x-h)^2+k\), to transform the graph of the parent function \(f(x)=x^2\).

Stretch or compress the graph of \(f(x)=x^2\) vertically by the factor \(|a|\).
If \(a\le0\), reflect the graph across the x–axis.
Shift the graph \(|h|\) units horizontally and \(|k|\) units vertically.

示例： Using Vertex Form

What is the graph of \(f(x)=-2(x-1)^2+3\)?

\(y=x^2,\ \pm2x^2,\ -2(x-1)^2+3\)

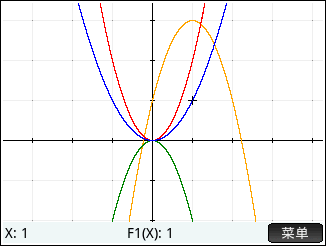
示例： Using Vertex Form

What steps transform the graph \(y=x^2\) to \(y=-\dfrac{1}{4}(x+1)^2+3\)?

What is the graph of \(y=-\dfrac{1}{4}(x+1)^2+3\)?

示例： Writing a Quadratic Function in Vertex Form

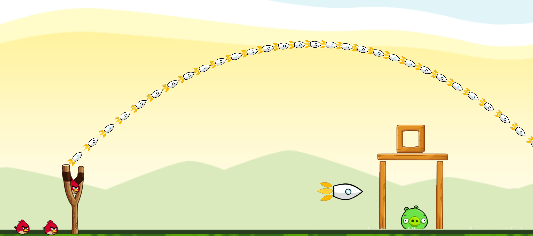
Fig 6 shows the path of an angry bird. What quadratic function models the path?

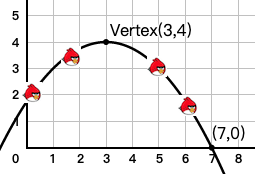
解：

Step 1\(\qquad\) The vertex is \((3,4)\).

\(\qquad\qquad\qquad\qquad\) \(h=3,\ k=4\)

Step 2\(\qquad\) Choose another point, (7,0), from the path.

\(\qquad\qquad\quad\) Substitute in the vertex form: \[\begin{align*} f(x)&=a(x-h)^2+k\\ 0&=a(7-3)^2+4 \end{align*}\]

Step 3\(\qquad\) Solve for \(a\). \[\begin{align*} 0&=16a+4\\ a&=-\dfrac{1}{4} \end{align*}\]

Conclusion\(\qquad\) \(f(x)=-\dfrac{1}{4}(x-3)^2+4\) modes the path.

☐

Standard Form of a Quadratic Function

In the previous section, you worked with quadratic functions written in vertex form. Now you will use quadratic functions in standard form. The standard form of a quadratic function is \(f(x)=ax^2+bx+c\), where \(a\neq0\).

y–intercept: y 轴截距

Properties of Quadratic Function in Standard Form

\(\quad\)(1) The graph of \(f(x)=ax^2+bx+c,\ a\neq0\) is a parabola.

\(\quad\)(2) If \(a>0\), the parabola opens upward.

\(\qquad\quad\)If \(a<0\), the parabola opens downward.

\(\quad\)(3) The axis of symmetry is the line \(x=-\dfrac{b}{2a}\).

\(\quad\)(4) The coordinate of the vertex is \((-\dfrac{b}{2a},f(-\dfrac{b}{2a}))\).

\(\quad\)(5) The y–intercept is \((0,c)\).

示例： Why It Works

Translate the standard form of quadratic functions, \(ax^2+bx+c=0\), into vertex form.

示例：

What is the graph of \(y=x^2+2x+3\)?

解：

Step 1\(\qquad\) Identify \(a\), \(b\) and \(c\). \[a=1,\ b=2,\ c=2\]

Step 2\(\qquad\) The axis of symmetry is \(x=-\dfrac{b}{2a}\). \[x=-1\]

\(\qquad\qquad\quad\) Lightly sketch the line \(x=-1\).

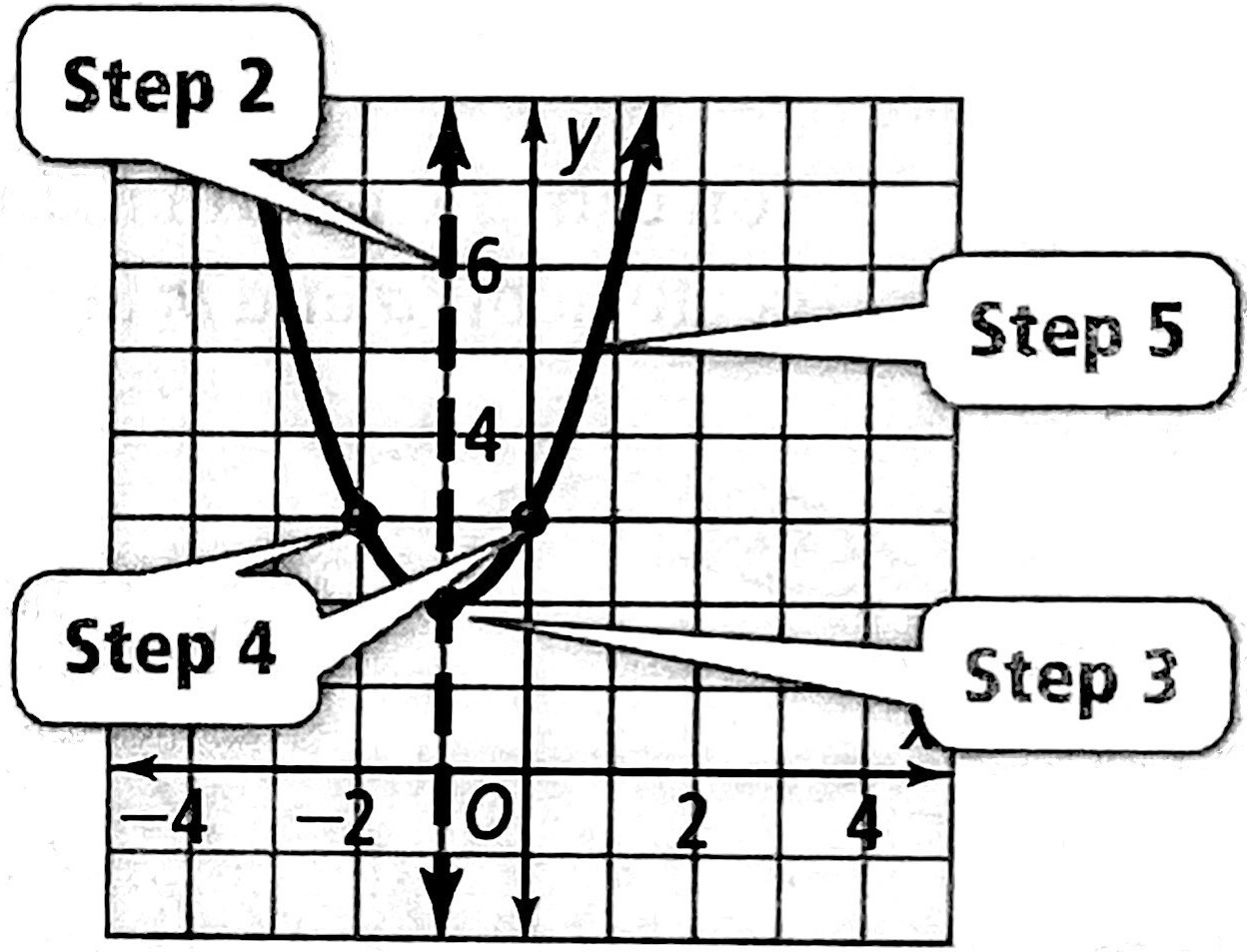
Step 3\(\qquad\) The x–coordinate of the vertex is also \(-\dfrac{b}{2a}\) or \(-1\).

\(\qquad\qquad\quad\) The y–coordinate is \(y=(-1)^2+2(-1)+3=2\).

\(\qquad\qquad\quad\) Plot the vertex \((-1,2)\).

Step 4\(\qquad\) Since \(c=3\), the y–intercept is \((0,3)\).

\(\qquad\qquad\quad\) The reflection of \((0,3)\) across \(x=-1\) is \((-2,3)\).

\(\qquad\qquad\quad\) Plot both points.

Step 5\(\qquad\) \(a>0\) confirms that the graph opens upward.

\(\qquad\qquad\quad\) Draw a smooth curve through the points you found in Steps 3 and 4.

☐

示例： Converting Standard Form to Vertex Form

What is the vertex form of \(f(x)=4x^2+8x+10\) ?

Solution 1

Step 1\(\qquad\) Compare: \(f(x)=4x^2+8x+10\)

\(\qquad\qquad\qquad\qquad\quad\) \(f(x)=a(x-h)^2+k=ax^2-2ahx+k-2ah^2\)

\(\qquad\qquad\quad\) \(a=4\)

Step 2\(\qquad\) \(-2ah=8\). Solve for h.

\(\qquad\qquad\quad\) \(h=-1\)

Step 3\(\qquad\) \(k-2ah^2=10\). Solve for k.

\(\qquad\qquad\quad\) \(k=6\)

Conclusion\(\qquad\) \(f(x)=4(x+1)^2+6\).

☐

Solution 2

Step 1\(\qquad\) Find the coordinate of the vertex.

\(\qquad\qquad\quad\) \(\left(-\dfrac{b}{2a},f(-\dfrac{b}{2a})\right)=(-1,f(-1))=(-1,6)\)

Step 2\(\qquad\) The standard and vertex form have the same ‘a’.

\(\qquad\qquad\quad\) \(a=4\), \(h=-1\) and \(k=6\).

Conclusion\(\qquad\) \(f(x)=4(x+1)^2+6\)

☐

示例： Converting Standard Form to Vertex Form

What is the vertex form of \(yd=-x^2+4x-5\) ?

示例： Interpreting a Quadratic Graph

The New River Gorge Bridge with Fall Colors

Bridges The New River Gorge Bridge in West Virginia is the world’s largest steel single arch bridge. You can model the arch with the function \(y=-0.000498x^2+0.847x\), where \(x\) and \(y\) are in feet. How high above the river is the arch? How long is the section of bridge above the arch?

解：

Step 1\(\qquad\) Find the vertex of the arch.

\(\qquad\qquad\quad\) \(x=-\dfrac{b}{2a}=\dfrac{0.874}{2(-0.000498)}\approx850\)

\(\qquad\qquad\quad\) \(y=-0.000498(850)^2+0.847(850)\approx360\)

Step 2\(\qquad\) Find the height of the arch above its supports.

\(\qquad\qquad\quad\) The y–coordinates of the vertex is the beight of the arch above its supports.

\(\qquad\qquad\quad\) The arch is about \(360\ \mathrm{ft}\) above its supports.

Step 3\(\qquad\) Find the length of the bridge above the river.

\(\qquad\qquad\quad\) The x–coordinates of the vertex is half the length of the bridge above the arch.

\(\qquad\qquad\quad\) The length of that part of the bridge is about \(850 \mathrm{ft}+850 \mathrm{ft}=1700 \mathrm{ft}\) long.

示例： Interpreting a Quadratic Graph

The Zhaozhou Bridge in China is the oldest known arch bridge, dating to A.D. 605. You can model the support arch with the function \(f(x)=-0.001075x^2+0.131148x\), where \(x\) and \(y\) are measured in feet.

The Zhaozhou Bridge

How high is the arch above its supports.
Why does the model not have a constant term.

Exercises

练习： Determine whether each relation is a functions?

练习： Use the vertical-line test to determine whether each graph represents a functions?

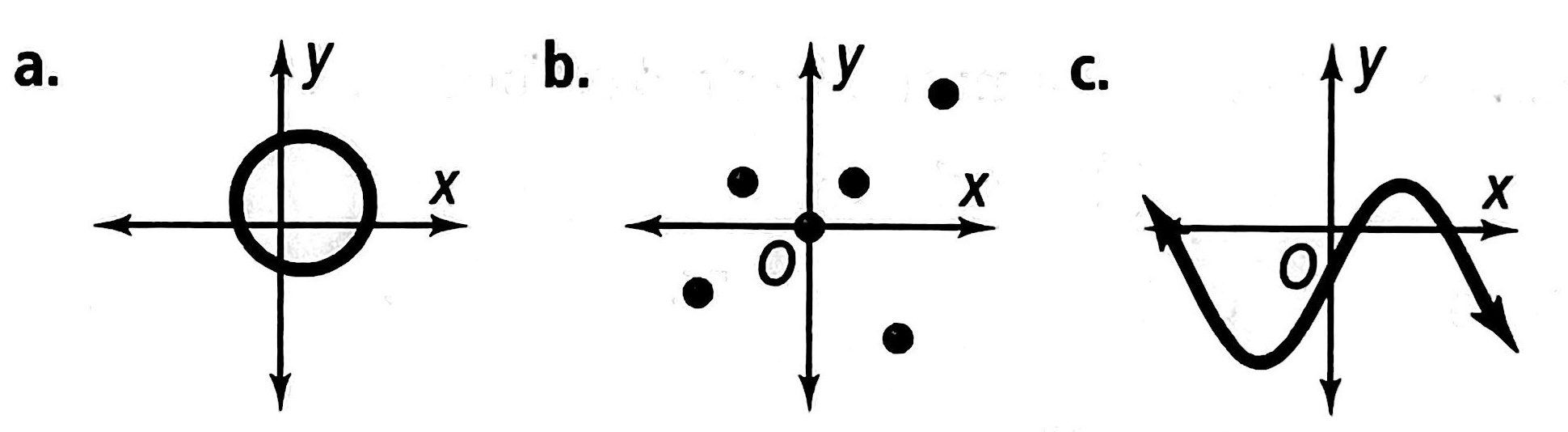
练习： Determine whether each graph represents a functions?

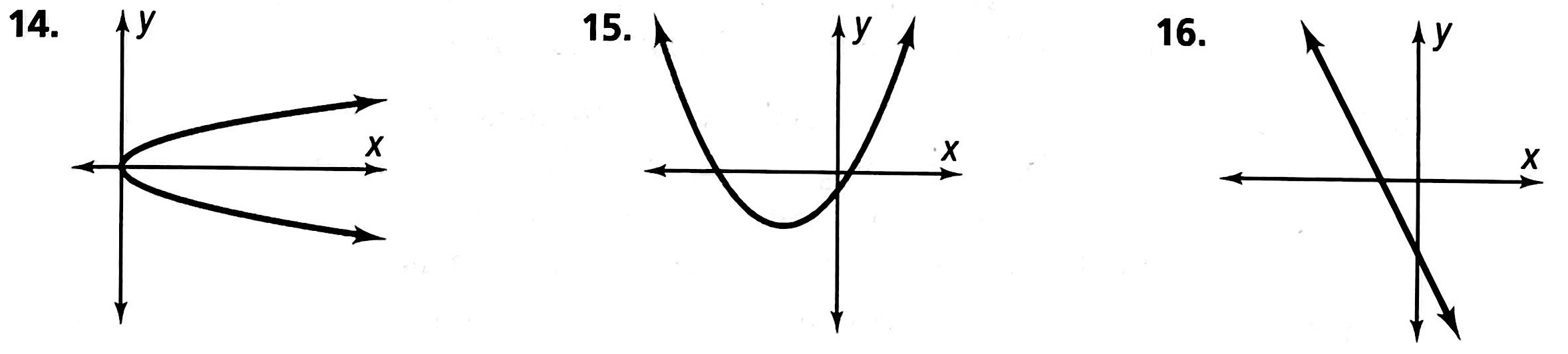
练习： Determine whether \(y\) is a function of \(x\). Explain.

\(\quad\)(1). \(y=\dfrac{3}{x}-11\) \(\qquad\) (2). \(y^2=3x-7\) \(\qquad\) (3). \(x^2=3y+y\)

练习： Graph each function.

\(\quad\)(1) \(f(x)=-x^2\) \(\qquad\) (2) \(f(x)=3x^2\) \(\qquad\) (3) \(f(x)=\dfrac{2}{5}x^2\)

练习： Graph each function.

\(\quad\) (1) \(f(x)=x^2+3\) \(\qquad\) (2) \(f(x)=-x^3+3\) \(\qquad\) (3) \(f(x)=(x-2)^2\)

练习： Graph each function.

\(\quad\)(1) \(f(x)=(x-1)^2+2\) \(\qquad\) (2) \(f(x)=-(x+1)^3+4\) \(\qquad\) (3) \(f(x)=2(x-2)^2+5\)

练习： Write a quadratic function to model each graph.

练习： Write the equation of each parabola in vertex form.

\(\quad\)(1) vertex \((1,2)\), point\((2,-5)\) \(\qquad\) (2) vertex \((-3,6)\), point \((1,-2)\)

\(\quad\)(3) vertex \((0,5)\), point\((2,-5)\) \(\qquad\) (4) vertex \((\dfrac{1}{4},-\dfrac{3}{2})\), point \((1,3)\)

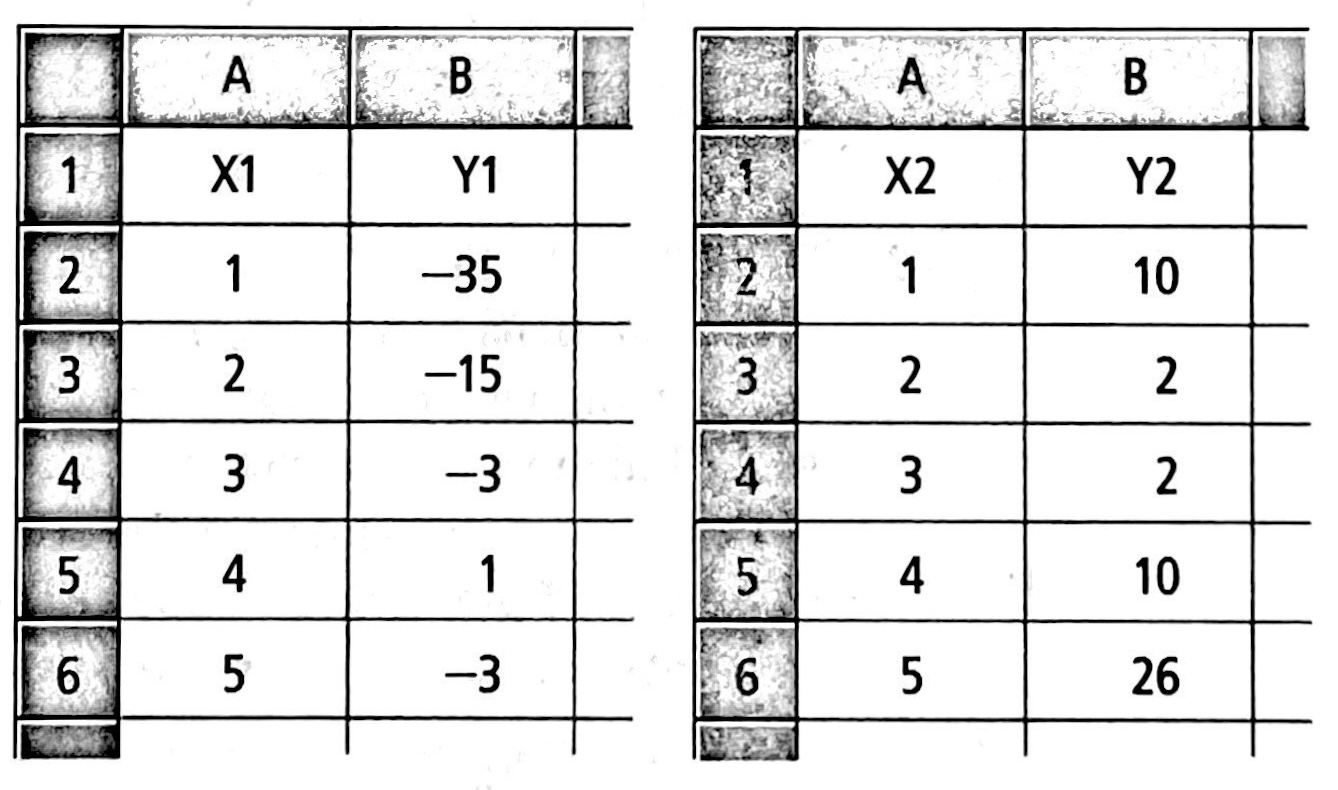
练习： Determine the vertex form for each parabola defined by the spreadsheet values at the right.

练习： Determine \(a\) and \(k\) so that given points are on the graph of the function.

\(\quad\)(1) \((0,1),(2,1)\); \(y=a(x-1)^2+k\) \(\quad\qquad\) (2) \((-3,2),(0,1)\); \(y=a(x+2)^2+k\)

\(\quad\)(3) \((1,11),(2,-19)\); \(y=a(x+1)^2+k\) \(\quad\) (4) \((-2,6),(3,1)\); \(y=a(x-3)^2+k\)

练习： Find the quadratic function \(y=a(x-h)^2\) whose graph passes througe the given points.

\(\quad\)(1) \((-2,1)\) and \((2,1)\) \(\qquad\) (2) \((-5,2)\) and \((-1,2)\) \(\qquad\) (3) \((-1,4)\) and \((7,-4)\)

\(\quad\)(4) \((2,-1)\) and \((4,0)\) \(\qquad\) (5) \((-5,18)\) and \((1,0)\) \(\qquad\) (6) \((1,-64)\) and \((-3,0)\)

练习： Write each function in vertex form.

\(\quad\)(1) \(y=x^2+4x+5\) \(\qquad\)(2) \(y=-2x^2+8x+17\) \(\qquad\) (3) \(y=4x^2+9x\)

\(\quad\)(4) \(y=\dfrac{1}{2}x^2-4x+7\) \(\qquad\) (5) \(y=-\dfrac{3}{2}x^2+6x+5\) \(\qquad\) (6) \(y=-\dfrac{1}{3}x^2+2x\)

练习： Graph each function.

\(\quad\)(1) \(y=x^2+6x+9\) \(\qquad\) (2) \(y=-x^2-3x+6\) \(\qquad\) (3) \(y=2x^2+4x\)

练习： Economics A model for a company’s revenue from selling a software package is \(R=-2.5p^2+500p\), where \(p\) is the price in dollars of the software. What price will maximize revenue? Find the maximum revenue.

练习： For each function, the vertex of the function’s graph is given. Find the unknown coefficients.

\(\quad\)(1) \(y=x^2+bx+c;\ (3,-4)\) \(\qquad\qquad\) (2) \(y=-3x^2+bx+c;\ (1,0)\)

\(\quad\)(3) \(y=ax^2+10x+c;\ (-5,-27)\) \(\qquad\) (4) \(y=c-ax^2-2x;\ (-1,3)\)

练习： For each function, the vertex of the function’s graph is given. Find the unknown coefficients.

\(\quad\)(1) \(y=ax^2+bx-27;\ (2,-3)\) \(\qquad\) (2) \(y=ax^2+bx+4;\ (-1,4)\)

\(\quad\)(3) \(y=ax^2+bx+8;\ (2,-4)\) \(\qquad\) (4) \(y=ax^2+bx;\ (-3,2)\)