均值不等式

基本不等式

基本不等式是主要应用于求某些函数的最值及证明的不等式。其表述为：两个正实数的算术平均数大于或等于它们的几何平均数。

基本不等式

若 $a,b>0$ ，则 $\dfrac{a+b}{2}\geq\sqrt{ab}$ ，当且仅当 $a=b$ 时取到等号。

证明基本不等式的方法有很多，以下摘录几种：

证明一 由于 $a,b>0$ ，故 $a=\sqrt{a}^2,\ b=\sqrt{b}^2$

将不等式左右相减得到： \[\dfrac{1}{2}(a+b-2\sqrt{ab})=\dfrac{1}{2}(\sqrt{a}-\sqrt{b})^2\geq0\]

等号仅在 $a=b$ 时取到，从而命题得证。

☐

证明二 当 $a,b>0$ 时：

$\dfrac{a+b}{2}\geq\sqrt{ab}\ \Leftrightarrow\ (a+b)^2\geq4ab\ \Leftrightarrow\ (a-b)^2\geq0$

命题 $(a-b)^2\geq0$ 为真，故 $\dfrac{a+b}{2}\geq\sqrt{ab}$ 亦为真。

等号仅在 $a=b$ 时取到，从而命题得证。

☐

证明三 设 $a+b=t,\ t>0$ 求得 $b=t-a,\ a\in(0,t)$

不等式左侧等于 $\dfrac{t}{2}$

不等式右侧变为 $\sqrt{a(t-a)}=\sqrt{-a^2+t\cdot a}$

根据二次函数的性质，$a=\dfrac{t}{2}$ 时，不等式左边取到最大值 $\dfrac{t}{2}$ 。

从而命题得证。

☐

证明四 根据平方根作图（射影定理）也可以说明二元均值不等式：

不等式证明基本技巧

示例：设 $a,b$ 是任意实数，求证 $a^4+b^4\geq a^3b+ab^3$ 。

解法一 将不等式左右两式相减：

解法一是《代数学辞典》给出的解法

\[\begin{align*} &a^4+b^4-a^3b-ab^3\\ =&(a-b)^2\cdot(a^2+ab+b^2)\\ =&(a-b)^2\cdot\left(\left(a+\dfrac{b}{2}\right)^2+\dfrac{3}{4}b^2\right) \geq0 \end{align*}\]

当且仅当 $a=b$ 时，$(a-b)^2=0$ ；

当且仅当 $a=b=0$ 时 $\left(a+\dfrac{b}{2}\right)^2+\dfrac{3}{4}b^2=0$ 。

综上所述，不等式成立，当且仅当 $a=b$ 时等号成立。

☐

思考与讨论

上述题目不等式两侧相减形成的对称式，你如何运用先前学过的对称式分解技巧进行分解？
除了配方，你还有什么方法说明 $a^2+ab+b^2$ 的非负性？

解法二 先证明一个引理：若 $x_1\geq x_2,\ y_1\geq y_2$ ，则 $x_1y_1+x_2y_2\geq x_1y_2+x_2y_1$

$x_1y_1+x_2y_2-x_1y_2-x_2y_1=(x_1-x_2)(y_1-y_2)\geq0$ ，引理得证。

不妨设 $a\geq b$ ，则 $a^3\geq b^3$ 。根据引理，$a^4+b^4\geq a^3b+ab^3$ 。

☐

思考与讨论

上述问题的一般形式是排序不等式。通俗地说就是为了让两两乘积之和最大，需要让大的乘大的，小的乘小的。请上网检索排序不等式的定义。

解法三 将不等式左右两式相减得到的结果 $a^4+b^4-a^3b-ab^3$ 看作 $a$ 的多项式 $f(a)$。

将问题看作求 $f(a)$ 的最小值：

$b=0$ 时，$f(a)=a^4$ ，易知在 $a=0$ 时取得最小值 $f(0)=0$ 。

$b\neq0$ 时，对 $a$ 求导数得到：

$f'(a)=4a^3-3a^2b-b^3=(a-b)(4a^2+ab+b^2)$

由于 $4a^2+ab+b^2$ 的判别式 $\Delta=-15b^2<0$ ，故 $f'(a)=0$ 的根只有 $a=b$ 。

从而易知 $f(a)$ 在 $a=b$ 时取到最小值 $f(b)=0$ 。

对于导数为 $0$ 的点，还需要额外一些讨论才能确定是最小值点。

综上所述，$f(a)$ 的最小值为 $0$ ，仅在 $a=b$ 时取到。因此不等式得证。

☐

示例：已知实数 $a,b,x,y$ 满足 $a^2+b^2=1,\ x^2+y^2=1$，求 $ax+by$ 的最大值。

解：均值不等式：

$2=a^2+x^2+b^2+y^2\geq2\sqrt{a^2x^2}+2\sqrt{b^2y^2}=2|ax|+2|by|\geq2(ax+by)$

上述不等式仅在 $a=x,\ b=y$ 时取到等号，有 $ax+by$ 的最大值为 $1$ 。

☐

解：三角换元 $a=\sin\alpha,\ b=\cos\alpha$ ，$x=\sin\beta,\ y=\cos\beta$

其中 $\alpha,\beta\in[0,2\pi)$ ，则有：

$ax+by=\sin\alpha\sin\beta+\cos\alpha\cos\beta=\cos(\alpha-\beta)\leq1$

等号仅在 $\alpha=\beta$ 时取到，即在 $a=x,\ b=y$ 时有最大值 $1$ 。

☐

解：令向量 $\vec{m}=\begin{bmatrix} a\\b \end{bmatrix}$ ，$\vec{n}=\begin{bmatrix} x\\y \end{bmatrix}$

根据 $a^2+b^2=1,\ x^2+y^2=1$ 可知 $\vec{m},\ \vec{n}$ 均是单位长度向量。

$ax+by$ 就是向量内积：

$ax+by=\vec{m}\cdot\vec{n}=|\vec{m}||\vec{n}|\cos\theta=\cos\theta$

其中 $\theta$ 是两个向量的夹角。

当两个向量同向时，即 $\theta=0$ 时，$ax+by$ 取到最大值 $1$ 。

☐

思考与讨论

上述不等式的背景是大名鼎鼎的柯西-布尼亚科夫斯基-施瓦茨不等式，简称柯西不等式。该不等式描述了两个向量的长度的乘积积与其内积绝对值的关系。请上网检索柯西不等式的定义。

背景资料：“柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。但从历史的角度讲,该不等式应称作Cauchy-Buniakowsky-Schwarz不等式（柯西-布尼亚科夫斯基-施瓦茨不等式）。因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式应用到近乎完善的地步。柯西不等式是由柯西在研究过程中发现的一个不等式,其在解决不等式证明的有关问题中有着十分广泛的应用,所以在高等数学提升中与研究中非常重要,是高等数学研究内容之一。” –《百度百科》

示例：证明对任意实数 $x,y,z$ 有 $(x+y+z)^2\geq3(xy+yz+zy)$

示例：¹ 设三角形的三边长为 $a,b,c$ ，比较 $(a+b+c)^2$ 与 $4(ab+bc+ca)$ 的大小。

示例：² $x,y$ 是正实数，比较 $(x^3+y^3)^{\frac{1}{3}}$ 与 $(x^2+y^2)^{\frac{1}{2}}$ 的大小。

示例：³ $x,y,z$ 是正实数，比较 $(x^3+y^3+z^3)^{\frac{1}{3}}$ 与 $(x^2+y^2+z^2)^{\frac{1}{2}}$ 的大小。

示例：⁴ 设 $a,b$ 是相异的正数，将 $\dfrac{2ab}{a+b}$ 、 $\dfrac{a+b}{2}$ 、$\sqrt{ab}$ 按大小排列，并证明你的结论。

示例：⁵ 设 $a,b$ 是正实数，证明 $\sqrt{2}$ 在以 $\dfrac{b}{a}$ 与 $\dfrac{2a+b}{a+b}$ 为端点的闭区间内。

示例：⁶ $a,b$ 是正实数，判断 $\dfrac{a^2}{b}+\dfrac{b^2}{a}$ 与 $a+b$ 的大小，并证明你的结论。

示例：⁷ 若 $a>b$ ，以下不等式是“一定成立”、“一定不成立”还是“有时成立”？

$\dfrac{2a+b}{a+2b}>\dfrac{a}{b}$
$a+\dfrac{1}{a}>b+\dfrac{1}{b}$
$\sqrt{\dfrac{b^2+1}{a^2+1}}>\dfrac{b}{a}$

示例：⁸ $a$ 是有理数， $b=\dfrac{a+2}{a+1}$ 。证明 $\sqrt{2}$ 在 $a$ 与 $b$ 之间，且距离 $b$ 比较近。

均值不等式（习题）

示例：⁹

2010.重庆.12} 已知 $t>0$ ，则函数 $y=\dfrac{t^2-4t+1}{t

$ 的最小值为 $\_\_\_\_\_$

示例：¹⁰

2004.湖北.8

已知 $x\geq\dfrac{5}{2}$ ，则 $f(x)=\dfrac{x^2-4x+5}{2x-4}$ 有 ()

A. 最大值 $\dfrac{5}{4}$ $\quad$ B. 最小值 $\dfrac{5}{4}$ $\quad$ C. 最大值 $1$ $\quad$ D. 最小值 $1$

示例：¹¹

2008.重庆.7

函数 $f(x)=\dfrac{\sqrt{x}}{x+1}$ 的最大值是 ()

A. $\dfrac{2}{5}$ $\qquad$ B.$\dfrac{1}{2}$ $\qquad$ C.$\dfrac{\sqrt{2}}{2}$ $\qquad$ D.$1$

示例：¹²

2010.山东.14} 若对任意 $x>0, \dfrac{x}{x^2+3x+1

a$ 恒成立，则 $a$ 的取值范围是 $\_\_\_\_\_$

示例：¹³

2006.陕西.7

$x,y$ 为正数，则 $(x+y)\left(\dfrac{1}{x}+\dfrac{4}{y}\right)$ 的最小值为 ()

A. $6$ $\qquad$ B. $9$ $\qquad$ C. $12$ $\qquad$ D. $15$

示例：¹⁴

2011.湖南.10

设 $x,y\in\mathbb{R}$ ，且 $xy\neq0$ ，则 $\left(x^2+\dfrac{1}{y^2}\right)\left(\dfrac{1}{x^2}+4y^2\right)$ 的最小值为 $\_\_\_\_\_$ 。

示例：¹⁵

2007.上海.8

$x,y\in \mathbb{R}^+$ ， $x+4y=1$ ，则 $xy$ 的最大值是 $\_\_\_$

示例：¹⁶

2004.重庆.14

$\dfrac{2}{x}+\dfrac{3}{y}=2,\ (x,y>0)$ ，则 $xy$ 的最小值是 $\_\_\_$

示例：¹⁷

2010.山东.14

$x,y\in\mathbb{R}^+$ ，且 $\dfrac{x}{3}+\dfrac{y}{4}=1$ ，则 $xy$ 的最大值为 $\_\_$

示例：¹⁸

2007.宁夏海南.7

已知 $x,y\geq0$ ， $x,a,b,y$ 成等差数列， $x,c,d,y$ 成等比数列，则 $\dfrac{(a+b)^2}{cd}$ 的最小值是（）

A.$0$B.$1$C.$2$D.$4$

示例：¹⁹

2008.江苏.11

设 $x,y,z$ 为正实数，满足 $x-2y+3z=0$ ， $\dfrac{y^2}{xz}$ 的最小值是 $\_\_\_\_\_$

示例：²⁰

2018.天津.13

已知 $a,b\in\mathbb{R}$ ，且 $a-3b+6=0$ ，则 $2^a+\dfrac{1}{8^b}$ 的最小值为 $\_\_\_\_\_$

示例：²¹

2009.重庆.7

$a>0, b>0$ ，则 $\dfrac{1}{a}+\dfrac{1}{b}+2\sqrt{ab}$ 的最小值是 ( )

A.$2$B.$2\sqrt{2}$C.$4$D.$5$

均值不等式（答案）

示例：²²

2010.重庆.12

已知 $t>0$ ，则函数 $y=\dfrac{t^2-4t+1}{t}$ 的最小值为 $\_\_\_\_\_$

解： $y=t-4+\dfrac{1}{t}\geq 2\sqrt{t\cdot \dfrac{1}{t}}-4=-2$

当 $t=\dfrac{1}{t}$ 即 $t=1$ 时取最小值 $-2$ 。

☐

示例：²³

2004.湖北.8

已知 $x\geq\dfrac{5}{2}$ ，则 $f(x)=\dfrac{x^2-4x+5}{2x-4}$ 有 ()

A. 最大值 $\dfrac{5}{4}$ $\quad$ B. 最小值 $\dfrac{5}{4}$ $\quad$ C. 最大值 $1$ $\quad$ D. 最小值 $1$

解： $f(x)=\dfrac{1}{2}\left(x-2+\dfrac{1}{x-2}\right)$ ， $x=3$ 时取最小值 $1$ ，故选 B

☐

示例：²⁴

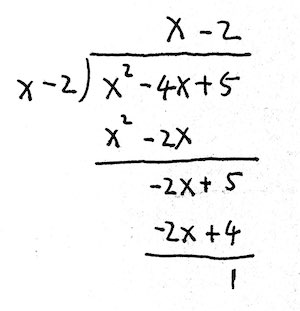
2008.重庆.7

函数 $f(x)=\dfrac{\sqrt{x}}{x+1}$ 的最大值是 ($\quad$)

A. $\dfrac{2}{5}$ $\qquad$ B.$\dfrac{1}{2}$ $\qquad$ C.$\dfrac{\sqrt{2}}{2}$ $\qquad$ D.$1$

解： $\dfrac{1}{f(x)}=\sqrt{x}+\dfrac{1}{\sqrt{x}}$ 最小值为 $2$ ，所以 $f(x)_{max}=\dfrac{1}{2}$ ，故选 B

☐

示例：²⁵

2010.山东.14

若对任意 $x>0,\ \dfrac{x}{x^2+3x+1}\leq a$ 恒成立，则 $a$ 的取值范围是 $\_\_\_\_\_$

解： $\because\ x>0,\ \dfrac{x^2+3x+1}{x}=3+x+\dfrac{1}{x} \in [5,+\infty)$

$\therefore\ x>0,\ \dfrac{x}{x^2+3x+1} \in (0,\dfrac{1}{5}]$

$\therefore\ a\in[\dfrac{1}{5},+\infty)$

示例：

2006.陕西.7} 设 $x,y$ 为正数，则 $(x+y)(+\dfrac{4}{y

)$ 的最小值为 ($\quad$)

A. $6$ $\qquad$ B. $9$ $\qquad$ C. $12$ $\qquad$ D. $15$

解： $(x+y)\left(\dfrac{1}{x}+\dfrac{4}{y}\right)=5+\dfrac{y}{x}+\dfrac{4x}{y}\geq5+2\sqrt{\dfrac{y}{x}\cdot\dfrac{4x}{y}}=9$

$\dfrac{y}{x}=\dfrac{4x}{y}$ 即 $y=2x$ 时取到等号。故选 B 。

☐

解： $\because\ \dfrac{x+y/2+y/2}{3}\geq\dfrac{3}{\dfrac{1}{x}+\dfrac{1}{y/2}+\dfrac{1}{y/2}}$

$\therefore\ (x+y/2+y/2)(\dfrac{1}{x}+\dfrac{1}{y/2}+\dfrac{1}{y/2})\geq9$

在 $x=y/2=y/2$ 时取到等号，故选 B 。

☐

示例：²⁶

2011.湖南.10

设 $x,y\in\mathbb{R}$ ，且 $xy\neq0$ ，则 $\left(x^2+\dfrac{1}{y^2}\right)\left(\dfrac{1}{x^2}+4y^2\right)$ 的最小值为 $\_\_\_\_\_$ 。

解：这个题跟上一道题本质上一码事儿，所以答案是 $9$ 。

☐

示例：²⁷

2007.上海.8

$x,y\in \mathbb{R}^+$ ， $x+4y=1$ ，则 $xy$ 的最大值是 $\_\_\_\_\_$

解： $xy=\dfrac{1}{4}\cdot x\cdot 4y = \dfrac{1}{4}\left(\sqrt{x\cdot4y}\right)^2\leq\dfrac{1}{4}\left(\dfrac{x+4y}{2}\right)^2=\dfrac{1}{16}$

$x=4y=\dfrac{1}{2}$ 时可以取到等号，故 $xy$ 的最大值是 $\dfrac{1}{16}$ 。

☐

示例：²⁸

2004.重庆.14

已知 $\dfrac{2}{x}+\dfrac{3}{y}=2,\ (x,y>0)$ ，则 $xy$ 的最小值是 $\_\_\_\_\_$

解：两个正数和一定 $\left(\dfrac{2}{x}+\dfrac{3}{y}\right)=2$ ，相等时乘积最大 $\left(\dfrac{6}{xy}\leq1\cdot1\right)$。

即：$\dfrac{2\cdot3}{x\cdot y}\leq\left(\dfrac{1}{2}\left(\dfrac{2}{x}+\dfrac{3}{y}\right)\right)^2=1$ ， $\dfrac{2}{x}=\dfrac{3}{y}=1$ 时取到等号。

故 $xy\geq6$ ，答案为 $6$ 。

☐

示例：²⁹

2010.山东.14

已知 $x,y\in\mathbb{R}^+$ ，且满足 $\dfrac{x}{3}+\dfrac{y}{4}=1$ ，则 $xy$ 的最大值为 $\_\_\_\_\_$

解： $\dfrac{x}{3}\cdot\dfrac{y}{4}\leq\dfrac{1}{2}\cdot\dfrac{1}{2}$ ，因此 $xy$ 最大值为 $3$ 。

☐

示例：³⁰

2007.宁夏海南.7

已知 $x,y\geq0$ ， $x,a,b,y$ 成等差数列， $x,c,d,y$ 成等比数列，则 $\dfrac{(a+b)^2}{cd}$ 的最小值是（）

A.$0$ $\qquad$ B.$1$ $\qquad$ C.$2$ $\qquad$ D.$4$

解： $\dfrac{(a+b)^2}{cd}=\dfrac{(x+y)^2}{xy}\geq\dfrac{(2\sqrt{xy})^2}{xy}=4$ ，选 D 。

☐

相等的时候最小，$x=y$ 时等于 $4$

示例：³¹

2008.江苏.11

设 $x,y,z$ 为正实数，满足 $x-2y+3z=0$ ， $\dfrac{y^2}{xz}$ 的最小值是 $\_\_\_\_\_$

解： $\dfrac{y^2}{xz}=\dfrac{(x+3z)^2}{x\cdot3z}\cdot\dfrac{3}{4}\geq4\cdot\dfrac{3}{4}=3$ ，在 $x=3z$ 时取到等号。

故 $\dfrac{y^2}{xz}$ 的最小值是 $3$ 。

☐

示例：³²

2018.天津.13

已知 $a,b\in\mathbb{R}$ ，且 $a-3b+6=0$ ，则 $2^a+\dfrac{1}{8^b}$ 的最小值为 $\_\_\_\_\_$

解： $2^a+\dfrac{1}{8^b}\geq2\sqrt{2^a\cdot2^{-3b}}=2\sqrt{2^{(a-3b)}}=2\sqrt{2^{-6}}=\dfrac{1}{4}$，

$a=-3b=-3$ 时取到等号。故 $2^a+\dfrac{1}{8^b}$ 的最小值为 $\dfrac{1}{4}$ 。

☐

示例：³³

2009.重庆.7

已知 $a>0, b>0$ ，则 $\dfrac{1}{a}+\dfrac{1}{b}+2\sqrt{ab}$ 的最小值是 ( )

A.$2$ $\qquad$ B.$2\sqrt{2}$ $\qquad$ C.$4$ $\qquad$ D.$5$

解： $\dfrac{1}{a}+\dfrac{1}{b}+2\sqrt{ab}>4\sqrt[4]{\dfrac{1}{a}\cdot\dfrac{1}{b}\cdot\sqrt{ab}\cdot\sqrt{ab}}=4$ ，当 $\dfrac{1}{a}=\dfrac{1}{b}=\sqrt{ab}$ 时等号成立。

故 $\dfrac{1}{a}+\dfrac{1}{b}+2\sqrt{ab}$ 的最小值是 $4$ ，选 C 。

☐

幂均不等式

如果 $a_1,a_2,a_3,\ ...\ a_n$ 是正实数，定义 $M_k$ 为： \[\begin{equation*} M_k= \begin{cases} \left(\dfrac{a_1^k+a_2^k+...+a_n^k}{n}\right)^{\dfrac{1}{k}} ,\qquad k\neq 0\\ \\ \sqrt[n]{a_1a_2...a_n}\ , \qquad\qquad\qquad\quad k=0 \end{cases} \end{equation*}\]

则对于 $k\in\mathbb{R}$ ， $M_k$ 是 $k$ 的单调递增函数。

当 $k=2,1,0,-1$ 时，$M_k$ 分别对应着：

平方平均数：$M_2=Q_n=\sqrt{\dfrac{x_1^2+x_2^2+...+x_n^2}{n}}$

算术平均数：$M_1=A_n=\dfrac{x_1+x_2+...+x_n}{n}$

几何平均数：$M_0=G_n=\sqrt[n]{x_1x_2...x_n}$

调和平均数：$M_{-1}=H_n=\dfrac{n}{\dfrac{1}{x_1}+\dfrac{1}{x_2}+...+\dfrac{1}{x_n}}$

均值不等式

调和平均数不超过几何平均数，几何平均数不超过算术平均数，算术平均数不超过平方平均数，简记为“调几算方”。均值不等式也可以看成是“对于若干个非负实数，它们的算术平均不小于几何平均”（AM-GM不等式）的推论。 \[H_n\leq G_n\leq A_n\leq Q_n\]

在上述结论中要求 $a_1,a_2,a_3,\ ...\ a_n$ 是正实数，主要是因为 $0$ 不能做分母。如果仅考虑 $k\geq0$ 的情况（平方平均、算术平均、几何平均），则要求非负实数就可以。如果只比较平方平均数和算术平均数，那对于任意实数都成立。

示例：求证算术平均值不小于几何平均值（AM-GM 不等式）：若$x_i\geq0,\ 1\leq i\leq n$ ，则 $\dfrac{x_1+x_2+...+x_n}{n}\geq\sqrt[n]{x_1x_2...x_n}$ 。当且仅当 $x_1=x_2=...=x_n=1$ 时等号成立。

引理若 $x_1,x_2,...,x_n>0,\ x_1x_2...x_n=1$ ，则 $x_1+x_2+...+x_n\geq n$ ，当且仅当 $x_1=x_2=...=x_n=1$ 时等号成立。

容易看出当 $x_1=x_2=...=x_n=1$ 时引理结论显然成立。

调整法第一步，观察取等条件

当诸 $x_i$ 不全相同时，则必存在大于 $1$ 和小于 $1$ 的 $x_i$ 。

挑一对这样的 $x_i$ 出来，不妨设为 $x_1,x_2$ 即 $x_1<1<x_2$ 。

将 $x_1,\ x_2$ 替换为 $x'_1=1,\ x'_2=x_1x_2$

调整法第二步，保持条件不变，向取等条件调整

因为 $(x_1-1)(x_2-1)<0$ ，所以 $x_1x_2+1<x_1x_2$ 。

这意味着 $x_1,\ x_2$ 到 $x'_1,\ x'_2$ 的替换，在积不变的同时降低了和。

$x'_1x'_2x_3...x_n=x_1x_2x_3...x_n=1$ 且

$x'_1+x'_2+x_3+...+x_n<x_1+x_2+x_3+...+x_n$

不断地如此替换，直至将所有的数都替换成 $1$ ，有

$x_1+x_2+x_3+...+x_n>1+1+...+1=n$

注意到在替换过程中，都是大于关系，都相等时命题的等号关系才成立

综合 $x_1=x_2=...=x_n=1$ 时的情况，引理得证。

证明下面我们来证明 AM-GM 不等式：

若某个 $x_i=0$ ，有 $\sqrt[n]{x_1x_2...x_n}=0$ 命题显然成立。

若 $x_i>0,\ 1\leq i\leq n$ ，令 $y_i=\dfrac{x_i}{\sqrt[n]{x_1x_2...x_n}}$，有 $y_1y_2...y_n=1$

由引理得到 $y_1+y_2+...+y_n\geq n$ （当且仅当 $y_1=y_2=...=y_n$时等号成立）

$\Leftrightarrow \dfrac{x_1+x_2+x_3+...+x_n}{\sqrt[n]{x_1x_2...x_n}}\geq n$

$\Leftrightarrow \quad \dfrac{x_1+x_2+...+x_n}{n}\geq\sqrt[n]{x_1x_2...x_n}$

当且仅当 $x_1=x_2=...=x_n=1$ 时等号成立。

☐

证明二 当 $n=2$ 时，不等式显然成立。

不等式对 $n$ 成立，那么它对 $n$ 也成立。这是由于：

$x_1+x_2...+x_{2n}\geq n\sqrt[n]{x_1x_2...x_n}+n\sqrt[n]{x_{n+1}x_{n+2}...x_{2n}}\geq 2n\sqrt[2n]{x_1x_2...x_{2n}}$

接下来我们准备使用归纳法：（柯西归纳法）

假设不等式对某个 $n$ 成立：

归纳假设

设 $x_n=\dfrac{x_1+x_2+...+x_{n-1}}{n-1}$ ，有

我们要证明对 $n-1$ 也成立

$x_1+x_2+...+x_{n-1}+\dfrac{x_1+x_2+...+x_{n-1}}{n-1}\geq n\sqrt[n]{x_1x_2...x_{n-1}\cdot\dfrac{x_1+x_2+...+x_{n-1}}{n-1}}$

$\dfrac{x_1+x_2+...+x_{n-1}}{n-1}\geq \sqrt[n]{x_1x_2...x_{n-1}\cdot\dfrac{x_1+x_2+...+x_{n-1}}{n-1}}$

$\left(\dfrac{x_1+x_2+...+x_{n-1}}{n-1}\right)^{\frac{n-1}{n}}\geq \left(x_1x_2...x_{n-1}\right)^{\frac{1}{n}}$

$\dfrac{x_1+x_2+...+x_{n-1}}{n-1}\geq\sqrt[n-1]{x_1x_2...x_{n-1}}$

因此不等式对 $n-1$ 也成立。从而对所有的自然数 $n$ 都成立。当且仅当 $x_1=x_2=...=x_n$ 时等号成立。

☐

示例：求证平方平均数不小于几何平均数，即 \[\sqrt{\dfrac{x_1^2+x_2^2+...+x_n^2}{n}}\geq\dfrac{x_1+x_2+...+x_n}{n}\]

等号当且仅当 $x_1=x_2=...=x_n$ 时成立。

证明设 $x_1+x_2+...+x_n=a$

只需证明 $x_1^2+x_2^2+...+x_n^2\geq\dfrac{a^2}{n}$

设 $x_i$ 不全相同，由对称性不妨设 $x_1<\dfrac{a}{n}<x_2$

则$\left(x_1-\dfrac{a}{n}\right)\left(\dfrac{a}{n}-x_2\right)<0$

$\Leftrightarrow\quad x_1x_2+\left(\dfrac{a}{n}\right)^2<\dfrac{1}{n}\left(x_1+x_2\right)$

$\Leftrightarrow\quad \left(\dfrac{a}{n}\right)^2+\left(x_1+x_2-\dfrac{a}{n}\right)^2<x_1^2+x_2^2$

令 $x'_1=\dfrac{a}{n},\ x'_2=x_1+x_2-\dfrac{a}{n},\ x'_3=x_3,\ ...\ ,\ x'_n=x_n$

有 ${x'_1}^2+{x'_2}^2+...+{x'_n}^2<x_1^2+x_2^2+...x_n^2$

如此不断替换，直至 $x_i$ 均为 $\dfrac{a}{n}$

于是 $x_1^2+x_2^2+...+x_n^2>\left(\dfrac{a}{n}\right)^2+\left(\dfrac{a}{n}\right)^2+...+\left(\dfrac{a}{n}\right)^2\geq\dfrac{a^2}{n}$

因此，$x_1^2+x_2^2+...+x_n^2\geq\dfrac{a^2}{n}$，等号只在 $x_1=...=x_n$ 时成立。

综上所述，命题得证。

☐

示例：求证几何平均值不小于调和平均值，即：

若 $a_k>0,\ k=1,2,...,n$ 则 $\sqrt[n]{a_1a_2...a_n}\geq\dfrac{n}{\frac{1}{a_1}+\frac{1}{a_2}+...+\frac{1}{a_n}}$

证明由 AM-GM 不等式有 \[\dfrac{1}{n}\left(\dfrac{1}{a_1}+\dfrac{1}{a_2}+...+\dfrac{1}{a_n}\right)\geq\sqrt[n]{\dfrac{1}{a_1}\cdot\dfrac{1}{a_2}\cdot...\cdot\dfrac{1}{a_n}}\]

两边取倒数，命题即得证。

☐

柯西-施瓦茨不等式

柯西不等式的内积表示

在实内积空间的向量 $\vec{a}$ 和 $\vec{b}$ 满足 $\vec{a}\cdot\vec{b}\leq||\vec{a}|| ||\vec{b}||\|$

如果二元映射 $\langle x,y\rangle:H\times H\rightarrow\mathbb{R}$ 满足以下性质，我们就认为其是一个“内积”：

$\quad$ (1) $<x,y>=<y,x>$

$\quad$ (2) $<x,x>\geq0$ 且 $<x,x>=0 \Leftrightarrow x=0$

$\quad$ (3) $<z,\alpha x+\beta y>=\alpha<z,x>+\beta<z,y>$

(笹部贞世郎 1982) - 570页 - 2334 题↩︎
(笹部贞世郎 1982) - 571页 - 2342 题(1)↩︎
(笹部贞世郎 1982) - 571页 - 2342 题(2)↩︎
(笹部贞世郎 1982) - 571页 - 2343 题↩︎
(笹部贞世郎 1982) - 571页 - 2340 题改↩︎
(笹部贞世郎 1982) - 571页 - 2344 题(1)↩︎
(笹部贞世郎 1982) - 573页 - 2348 题↩︎
(笹部贞世郎 1982) - 574页 - 2351 题↩︎
(朱昊鲲 2019)-page101-880 ↩︎
(朱昊鲲 2019)-page101-881↩︎
(朱昊鲲 2019)-page101-882↩︎
(朱昊鲲 2019)-page101-883↩︎
(朱昊鲲 2019)-page101-884↩︎
(朱昊鲲 2019)-page101-885↩︎
(朱昊鲲 2019)-page101-886↩︎
(朱昊鲲 2019)-page101-887↩︎
(朱昊鲲 2019)-page101-888↩︎
(朱昊鲲 2019)-page101-889↩︎
(朱昊鲲 2019)-page101-890↩︎
(朱昊鲲 2019)-page101-891↩︎
(朱昊鲲 2019)-page101-892↩︎
(朱昊鲲 2019)-page101-880 ↩︎
(朱昊鲲 2019)-page101-881↩︎
(朱昊鲲 2019)-page101-882↩︎
(朱昊鲲 2019)-page101-883↩︎
(朱昊鲲 2019)-page101-885↩︎
(朱昊鲲 2019)-page101-886↩︎
(朱昊鲲 2019)-page101-887↩︎
(朱昊鲲 2019)-page101-888↩︎
(朱昊鲲 2019)-page101-889↩︎
(朱昊鲲 2019)-page101-890↩︎
(朱昊鲲 2019)-page101-891↩︎
(朱昊鲲 2019)-page101-892↩︎

均值不等式

基本不等式

不等式证明基本技巧

均值不等式（习题）

均值不等式（答案）

幂均不等式

柯西-施瓦茨不等式

参考文献