直线与线性方程组

直线与线性方程组

线性函数和直线的斜截式

由两点确定直线的斜率

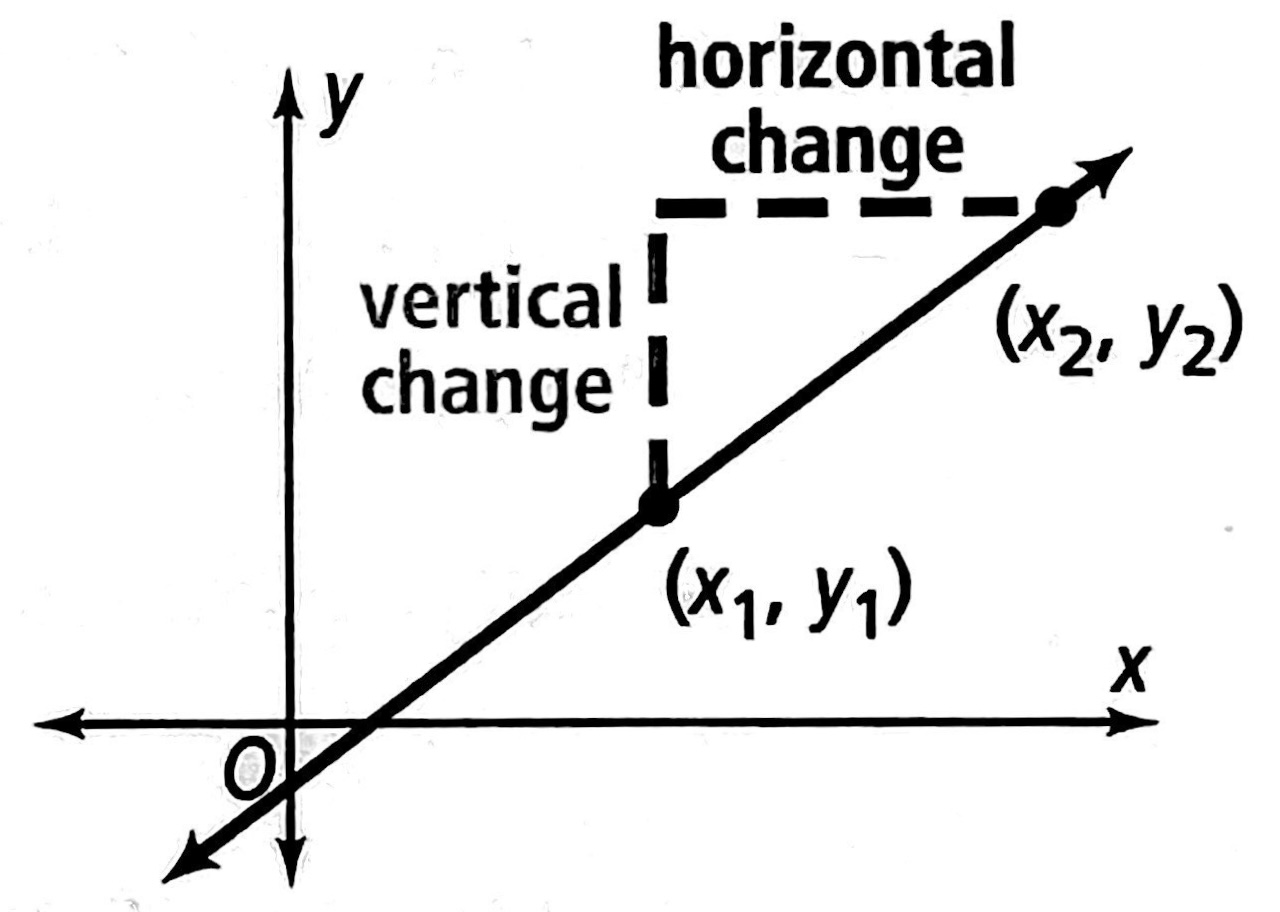
直线的斜率

定义直线的斜率为垂直方向坐标的变化量与竖直方向坐标的变化量之比。即对于过点 \((x_1,y_1)\) 和 \((x_2,y_2)\) 的直线，其斜率为： \[\mathbf{k}=\dfrac{y_2-y_1}{x_2-x_1}\]

示例： 计算直线的斜率

过以下两点做直线，斜率分别是多少？ 在坐标格中画出上述直线。

A. \((-3,7)\) and \((-2,4)\)B. \((3,1)\) and \((-4,1)\)

斜率的存在性

当我们讨论斜率时，前提是直线的斜率存在。竖直（与 \(x\) 轴垂直）的直线没有斜率。在使用斜率相关的数学工具解决问题时，你需要单独讨论斜率不存在的情形。令人欣慰的是，斜率不存在的情形往往比较简单。

线性函数

在初级代数与解析几何，线性函数是只拥有一个变量的一阶多项式函数，又或者是常数函数。因为，采用直角坐标系，这些函数的图象是直线，所以，这些函数是线性的。要注意的是，与x轴垂直的直线不是线性函数。（因为输入值不对应唯一输出值，所以它不符合函数的定义）《百度百科》

直线的截距

直线的截距是直线和坐标轴的交点坐标。与 \(x\) 轴的交点坐标称为 \(x\) 轴截距或横截距，与 \(y\) 轴的交点坐标称为 \(y\) 轴截距或纵截距。

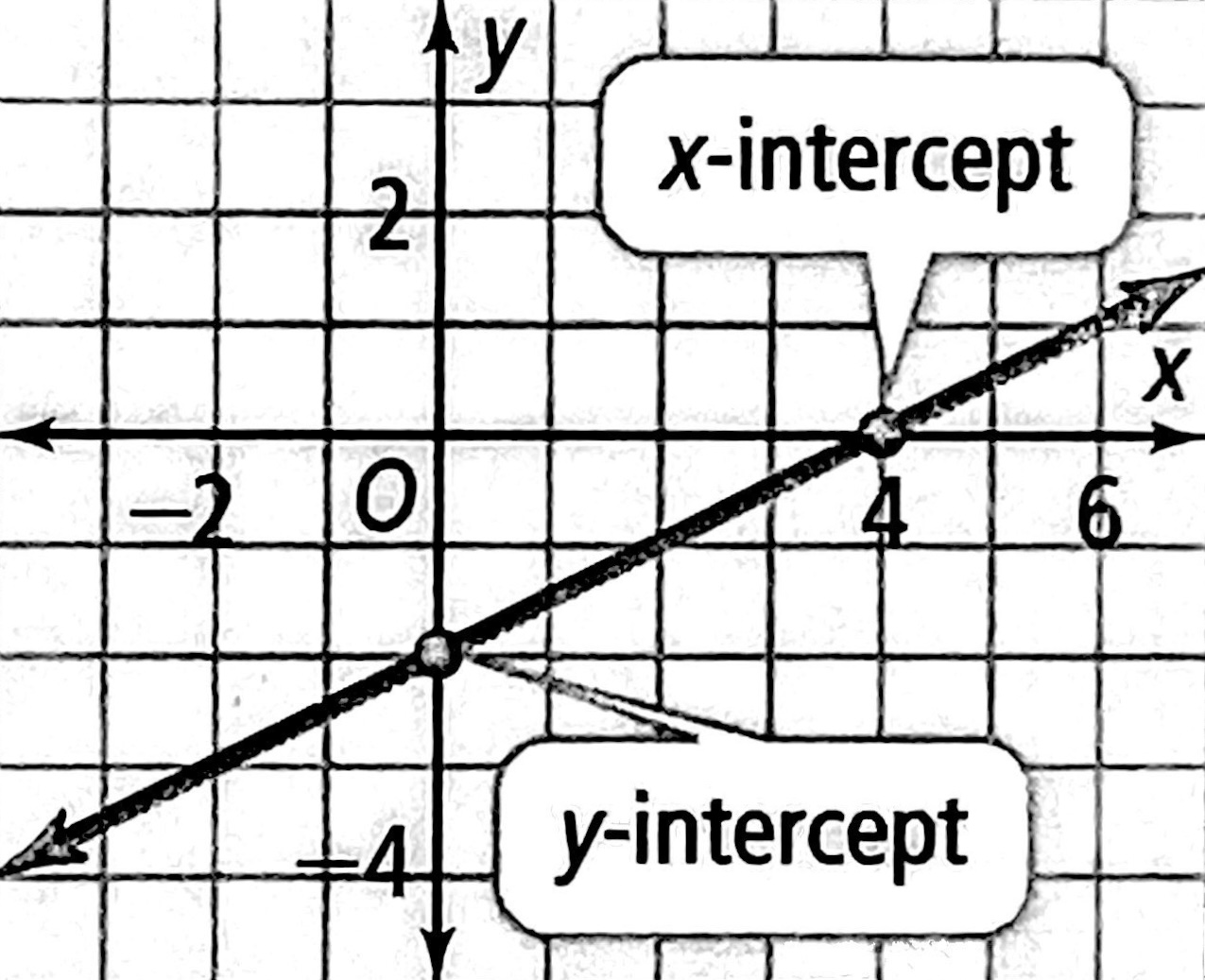
直线的斜截式

直线的斜截式方程如下所示： \[y=kx+b\] 其中 \(k\) 是直线的斜率，\(b\) 是直线的 \(y\) 轴截距。

示例： 根据条件求直线的方程

以下各直线的斜截式方程是什么?

A. 直线的斜率 \(k=\dfrac{1}{5}\) ，与\(y\) 轴交点是 \((0,-3)\)

B. 直线过点 \((1,2)\)，斜率 \(k=\dfrac{1}{5}\)

C. 直线过点 \((4,3)\) ，与 \(y\) 轴的交点为 \((0,-3)\)

示例： 根据条件求直线方程

下图中的直线对应的方程是什么?

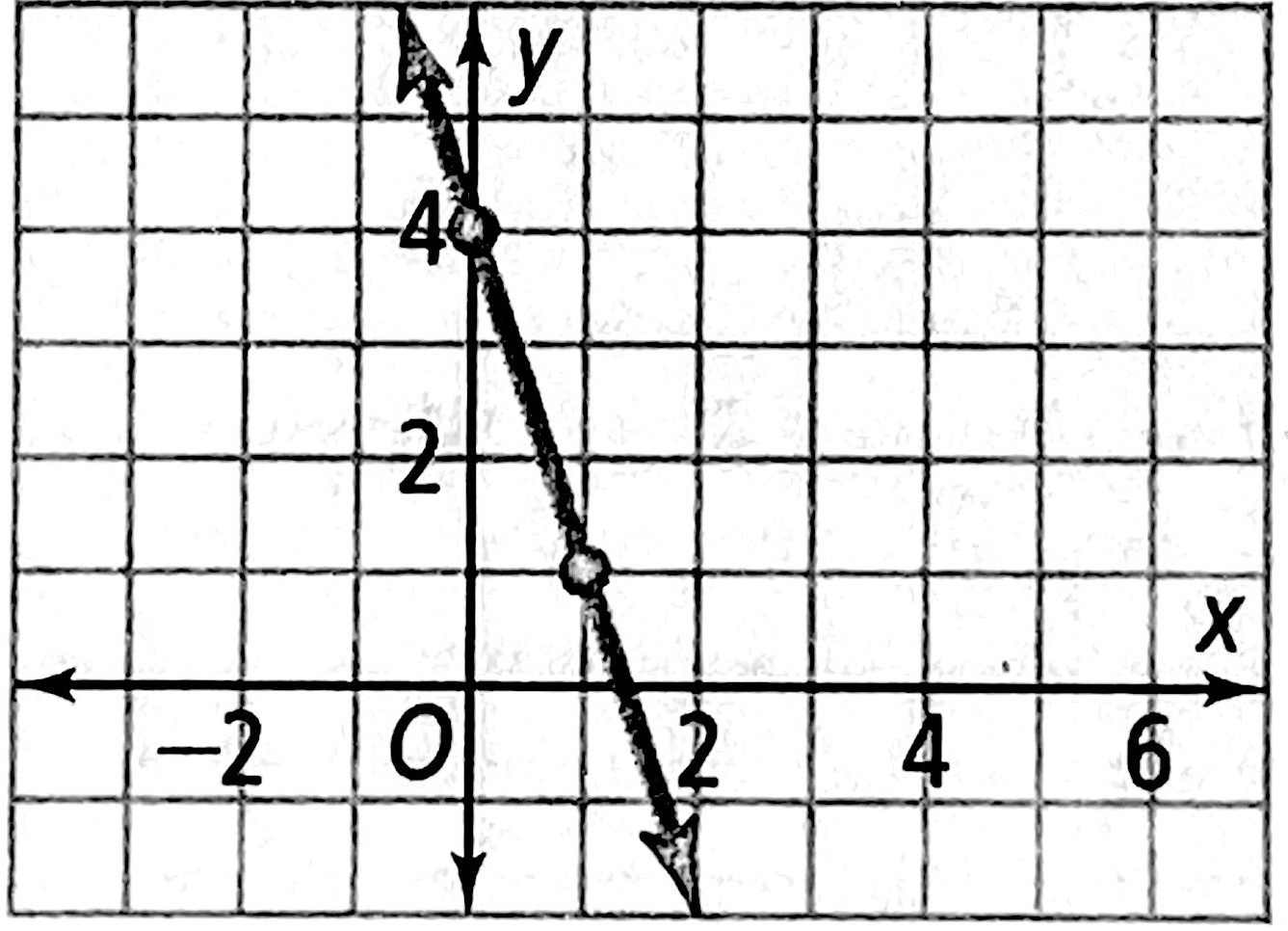A. B.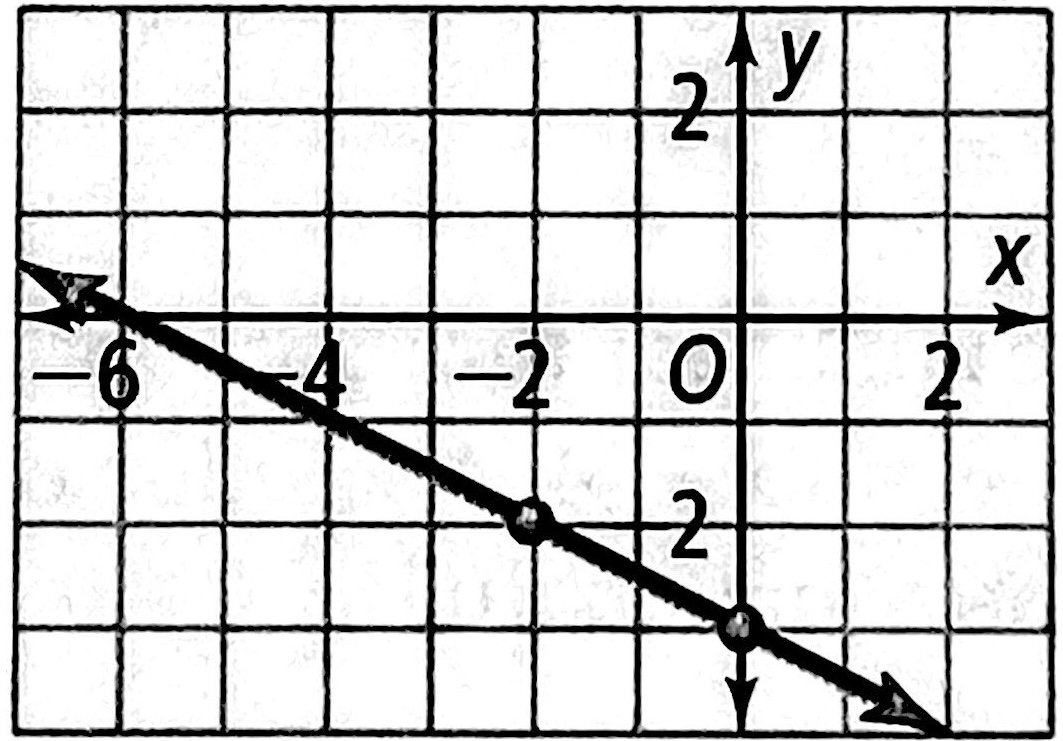

示例： 将直线方程写成斜截式

写出以下直线方程的斜截式。直线斜率和截距分别是什么？

A. \(5x-4y=16\)B. \(-\dfrac{3}{4}x+\dfrac{1}{2}y=-1\)

示例： 绘制直线方程的图像

绘制 \(-2x+y=1\) 的图像

示例： 绘制直线方程的图像

绘制 \(4x-7y=14\) 的图像

示例： 绘制直线方程的图像

绘制 \(3x+4y=12\) 的图像

直线方程的点斜式和标准式

除了斜截式外，直线方程还有其它常见的形式，如点斜式和标准式。

直线的点斜式

经过点 \((x_1,y_1)\) ，斜率为 \(k\) 的直线可以表示为点斜式: \[y-y_1=m(x-x_1)\]

示例： 写出直线的点斜式方程

直线过点 \((-5,2)\) ，斜率为 \(\dfrac{3}{5}\) 。写出直线的一个点斜式方程。

示例： 写出直线的点斜式方程

直线经过两点 \((3,2)\) and \((5,8)\) 。写出直线的一个点斜式方程。

示例： 写出直线的点斜式方程

直线在 \(x\) 轴的截距为 \(3\) ， \(y\) 轴截距为 \(4\) 。写出直线的一个点斜式方程。

示例： 写出直线的点斜式方程

直线的斜截式方程为 \(y=2x+1\)。写出直线的一个点斜式方程。

直线的标准式

直线的标准式方程的形式为： \[Ax+By=C\] 其中 \(A,B,C\) 是实数，且 \(A,B\) 不全为 \(0\) 。

示例： 写出直线的标准式方程

将直线 \(y=\dfrac{3}{4}x-5\) 写做标准式方程，要求使用整系数和常数项。

示例： 根据标准式计算截距绘制直线图形

求直线 \(3x+5y=15\) 的截距，再根据截距绘制直线的图形。

直线的平行和垂直关系

平行直线的斜率相等，反之亦然。

两直线斜率互为负倒数，则两直线垂直。

如果直线的斜率存在，且两直线垂直，则斜率互为负倒数。

平行和垂直

示例： 平行线和垂线的方程

写出所求直线的斜截式方程：

A. 平行于 \(y=6x-2\) 且经过点 \((1,-3)\) 的直线
B. 垂直于 \(y=-4x+\dfrac{2}{3}\) 且经过点 \((8,5)\) 的直线

直线的两点式方程和参数方程

本页为补充笔记，涉及两点式方程、参数方程和正弦余弦、斜率和正切的关系

用图像和表格解二元一次线性方程组

当我们处理涉及多个关联未知量的问题时，可以将其表示为多个方程组成的方程组。

线性方程组和方程组的解

线性方程组由多个线性方程组成。一组能够让方程组中的全部方程都成立的变量的值称为方程组的解。

示例： 解线性方程组

解线性方程组 $ \[\begin{cases} -3x+2y&=8\\ \quad x+2y&=-8 \end{cases}\]

$

方法一 图像法
方法二 表格法（略）

二元一次线性方程组解的存在性

我们根据解的数量将线性方程组分类：

二元一次线性方程组解的情形

二元一次方程组解的分类

示例： 判断二元一次方程组解的存在性

不画图判断下列方程组解的存在性

A.\(\begin{cases}-3x+y&=4\\\quad x-\dfrac{1}{3}y&=1\end{cases}\) \(\qquad\) B. \(\begin{cases}2x+3y&=1\\\quad 4x+y&=-3\end{cases}\) \(\qquad\) C. \(\begin{cases}&y=2x-3\\\quad &6x-3y=9\end{cases}\)

使用代数变换求解二元一次方程组

示例： 使用代入消元法解线性方程组

解方程组 \(\begin{cases}3x+4y&=12\\ 2x+y&=10\end{cases}\)

示例： 使用代入消元法解线性方程组

解方程组 \(\begin{cases}x+3y&=5\\ -2x-4y&=-5\end{cases}\)

示例： 使用代入消元法解线性方程组

解方程组 \(\begin{cases}6a+b&=300\\ 12a+b&=480\end{cases}\)

示例： 使用加减消元法解线性方程组

解方程组 \(\begin{cases}3x+4y&=12\\ 2x+y&=10\end{cases}\)

示例： 使用加减消元法解线性方程组

解方程组 \(\begin{cases}x+3y&=5\\ -2x-4y&=-5\end{cases}\)

示例： 使用加减消元法解线性方程组

解方程组 \(\begin{cases}6a+b&=300\\ 12a+b&=480\end{cases}\)

示例： 处理解非唯一解的线性方程组

以下方程的解是什么？

A.\(\begin{cases}-3x+y&=-5\\\quad 3x-y&=5\end{cases}\) B. \(\begin{cases}\quad4x-6y&=6\\ -4x+6y&=10\end{cases}\)

示例： 处理解非唯一解的线性方程组

以下方程的解是什么？

A.\(\begin{cases}-x+y&=-2\\ 2x-2y&=0\end{cases}\) B. \(\begin{cases}\quad4x+y&=6\\ 12x+3y&=18\end{cases}\)

用高斯消去法解三元一次线性方程组

示例： 解方程组 \(\begin{cases} 2x-y+z=4\\x+3y-z=11\\4x+y-z=14\end{cases}\)

解法一 方程组的求解过程如下：

因此方程组的解是 \(\begin{cases} x=3\\y=3\\z=1\end{cases}\)

☐


我们可以通过挑选消去的次序，简化运算，请看如下解法：

解法二 通过观察，发现先消去 \(z\) 比较便捷，求解过程如下：（请在右侧自行补充矩阵记法的求解过程。）

☐


示例： 求解线性方程组 \(\begin{cases} x-y+z=-1\\x+y+3z=-3\\2x-y+2z=0\end{cases}\)

示例： 求解线性方程组 \(\begin{cases} x+y+2z=3\\2x+y+3z=7\\-x-2y+z=10\end{cases}\)

示例： 求解线性方程组 \(\begin{cases} x-2y+3z=12\\2x-y-2z=5\\2x+2y-z=4\end{cases}\)

示例： 求解线性方程组 \(\begin{cases} x-y+z=-1\\x+y+3z=-3\\2x-y+2z=0\end{cases}\)

示例： 求解线性方程组 \(\begin{cases} x-y-2z=4\\-x+2y+z=1\\-x+y-3z=11\end{cases}\)

示例： 求解线性方程组 \(\begin{cases} -2x+y-z=2\\-x-3y+z=-10\\3x+6z=-24\end{cases}\)

示例： 求解线性方程组 \(\begin{cases} x+4y-5z=-7\\3x+2y+3z=7\\2x+y+5z=8\end{cases}\)

三元一次线性方程组的几何含义

在三维直角坐标系中，三元一次方程表示一个平面

示例： 在三维直角坐标系中绘制 \(x+y+z=1\) 所代表的平面。

SketchBook 手绘（左）和Ti Nspire 图形计算器（右）的绘图
\(x+y+z=1\) 绘图的动态效果
事实上，绘制三维空间线性方程的图像是挺费劲的，今天我们往往使用图形计算器或者计算机来绘制三维图像。在探索三维或更高维的空间时，代数手段往往更容易被人类的大脑接受。

☐


两个连立的三元一次线性方程组对应着两个平面。解有三种情况：（一）两个方程代表同一个平面，这意味着一个方程可以通过变换为另一个方程。这时方程组的解就是平面上的点的三维坐标；（二）两个方程代表的平面互相平行。这意味着两个方程可以变换为系数相同但常数项不同的方程。这时方程组没有解。（三）两个方程代表的平面不平行，这是最一般的情况，这是方程组的解就是两个平面的相交直线上点的三维坐标。

平面的法向量

垂直于平面的向量称为平面的法向量。对于方程 \(Ax+By+Cz=D\) 表示的平面来说，\((A,B,C)\) 是该平面的一个法向量。

示例： 在三维直角坐标系中绘制 \(\begin{cases} x+y+z=1\\x+y+z=2\end{cases}\)

两个方程代表的平面关系如何？方程组的解如何？

动画 \(x+y+z=1\) 和 \(x+y+z=2\) 的三维图像
\(x+y+z=1\) 和 \(x+y+z=2\) 的三维图像
解： 两个方程的法向量相同，都是 \((1,1,1)\) ，这意味着两个平面平行（事实上，平行只需要法向量同向或者反向即可）。而两个方程的常数项不同（ \(2\) 和 \(1\) ），所以两个方程代表一组平行平面。平行平面没有公共点，方程组无解。无解的事实从方程本身也可以看出： \(x+y+z\) 无法既等于 \(1\) 又等于 \(2\) 。

☐


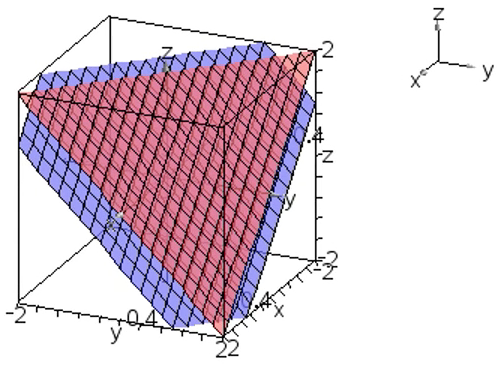
示例： 在三维直角坐标系中绘制 \(\begin{cases} x+y+z=1\\4x+y+z=2\end{cases}\)

两个方程代表的平面关系如何？方程组的解如何？

动画 \(x+y+z=1\), \(4x+y+z=2\)
\(x+y+z=1\), \(4x+y+z=2\)
解： 两个方程的法向量线性无关。这意味两个平面不平行。两个平面相交于一条直线，这条直线上所有点的三维坐标都是方程组的解。

☐


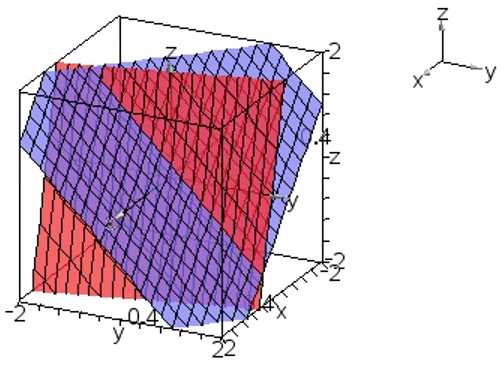
思考与讨论

示例： 在三维直角坐标系中绘制 \(\begin{cases} x+y+z=1 \qquad&(1)\\4x+y+z=2&(2)\\-2x+y+z=0&(3)\end{cases}\)

三个方程代表的平面关系如何？方程组的解如何？

解： 代表的平面相交于一条直线。

又因为 \((1)\cdot2-(2)=(3)\)，所以 \((3)\) 对解无影响。

这意味着平面 \((3)\) 经过 \((1),(2)\) 的相交直线。

\(x+y+z=1\) , \(4x+y+z=2\), \(-2x+y+z=0\)
所以这三个方程代表的平面相交于一条直线，该直线上所有的点的三维坐标都是方程组的解。

☐


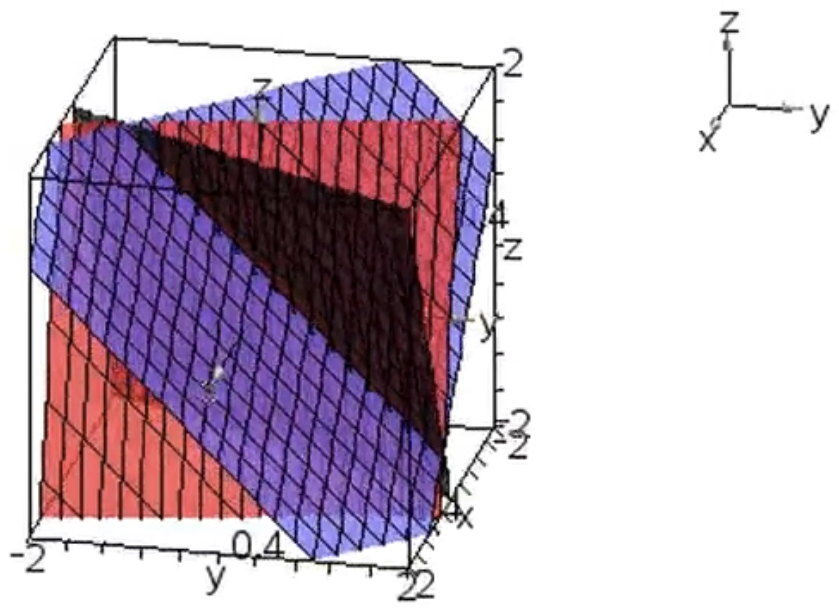
思考与讨论

示例： 在三维直角坐标系中绘制 \(\begin{cases} x+y+z=1 \qquad&\textcircled{1}\\4x+y+z=2&\textcircled{2}\\-2x+y+z=3&\textcircled{3}\end{cases}\)

三个方程代表的平面关系如何？方程组的解如何？

解： \(\textcircled{1}\cdot2-\textcircled{2}\) 得到 \(-2x+y+z=0\)

\(\textcircled{1},\textcircled{2}\) 线性组合得到了与 \(\textcircled{3}\) 系数相同但常数项不相同的方程。

\(x+y+z=1\) , \(4x+y+z=2\), \(-2x+y+z=3\)

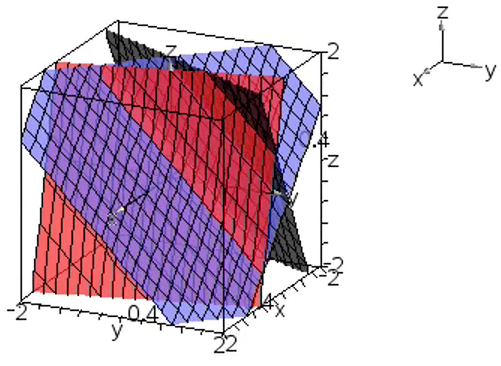
这意味着方程组无解。

本例中的三个方程所代表的平面互不平行，两两相交于一条直线，这三条直线互相平行。

☐


思考与讨论

示例： 在三维直角坐标系中绘制 \(\begin{cases} x+y+z=1 \qquad&\textcircled{1}\\4x+y+z=2&\textcircled{2}\\-2x+y+z=3&\textcircled{3}\end{cases}\)

三个方程代表的平面关系如何？方程组的解如何？

\(x+y+z=1\) , \(4x+y+z=2\), \(-2x+y+z=3\)

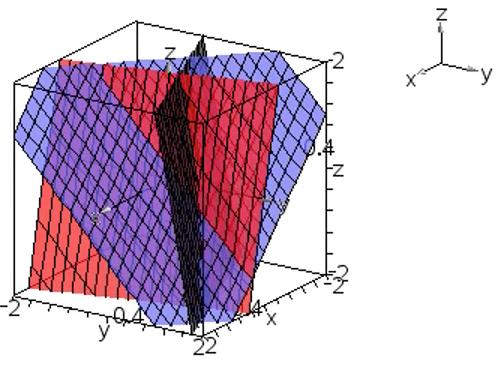
解： 这是最常见的方程组，三个系数向量（平面法向量）不共面。

任何两个平面的法向量的线性组合无法得到第三个。

三个方程所代表的平面相交于一点，方程组有唯一解。

☐


思考与讨论

基础练习

练习： 求以下直线的 \(x\) 轴和 \(y\) 轴截距

A. \(x-3y=0\) B. \(y=7x+5\)

C. \(y=6x\) D. \(-4x+y=10\)

练习： 求以下直线的斜截式方程

A. \(2x-y=9\) B. \(4x=2+y\)

C. \(5y=-3x-10\) D. \(4x+6y=12\)

练习： 写出以下直线方程的标准式方程（整数系数和常数项）

A. the line through \((2,3)\) and \((4,5)\)

B. the line through \((-4,6)\) and \((2,-2)\)

C. the line through \((-4,2)\) with slope \(3\)

D. the line through \((1,2)\) with slope \(\dfrac{4}{5}\)

E. the line through \((3,1)\) with slope \(0\)

F. the line with slope \(\dfrac{2}{3}\) and y–intercept \((0,5)\)

G. \(2y=-4x-12\)

H. \(\dfrac{2}{3}x+3=6y-15\)

练习： 根据给定两点确定的直线写出点斜式方程

A. \((-4,2)\) and \((-3,5)\) B. \((0,0)\) and \((-4,-5)\)

C. \((-4,-3)\) and \((2,7)\) D. \((-2,6)\) and \((0,2)\)

练习： 绘制直线方程的图像

A. \(2y=4x+8\) B. \(2x-3y=6\) C. \(4y-x=16\)

练习： 绘图求解二元一次方程组，并验算

A.\(\begin{cases}y&=x-2\\ y&=-2x+7\end{cases}\) B. \(\begin{cases} 2x+4y&=12\\ x+y&=2\end{cases}\)

练习： Write and solve a system of equations for each situation. Check your answers.

A. A Store sells small notebooks for \(\$8\) and large notebooks for \(\$10\). If you buy 6 notebooks and spend \(\$56\), how many of each size notebook did you buy?

B. A shop has one-pound bags of peanuts for \(\$2\) and three-pound bags of peanuts for \(\$5.50\). If you buy \(5\) bags and spend \(\$17\), how many of each size bag did you buy?

练习： 判断方程组解的存在性

A.\(\begin{cases}7x-y=6\\ -7x+y=-6\end{cases}\) B. \(\begin{cases} -3x+y=4\\ x-\dfrac{1}{3}y=1\end{cases}\) C.\(\begin{cases}4x+8y=12\\ x+2y=-3\end{cases}\)

D. \(\begin{cases} y=2x-1\\ y=-2x+5\end{cases}\) E. \(\begin{cases} 2y=5x+6\\ -10x+4y=8\end{cases}\) F. \(\begin{cases} x-3y=2\\ 4x-12y=8\end{cases}\)

G. \(\begin{cases} 2y-x=4\\ \dfrac{1}{2}x+y=2\end{cases}\) H. \(\begin{cases} x+4y=12\\ 2x-8y=4\end{cases}\) I. \(\begin{cases} 4y-2x=6\\ 8y=4x-12\end{cases}\)

练习： 用代入消元法解方程组并验算

A.\(\begin{cases}4x+2y=7\\ y=5x\end{cases}\) B. \(\begin{cases} 3c+2d=2\\ d=4\end{cases}\) C.\(\begin{cases}x+12y=68\\ x=8y-12\end{cases}\)

D. \(\begin{cases} 4p+2q=8\\ q=2p+1\end{cases}\) E. \(\begin{cases} x+3y=7\\ 2x-4y=24\end{cases}\) F. \(\begin{cases} x+6y=2\\ 5x+4y=36\end{cases}\)

G. \(\begin{cases} t=2r+3\\ 5r-4t=6\end{cases}\) H. \(\begin{cases} y=2x-1\\ 3x-y=-1\end{cases}\) I. \(\begin{cases} r+s=-12\\ 4r-6s=12\end{cases}\)

练习： 用加减消元法解方程组，并验算

A.\(\begin{cases}4x-6y=-26\\ -2x+3y=13\end{cases}\) B. \(\begin{cases} 9a-3d=3\\ -3a+d=-1\end{cases}\) C.\(\begin{cases}2a+3b=12\\ 5a-b=13\end{cases}\)

D. \(\begin{cases} 2x-3y=6\\ 6x-9y=9\end{cases}\) E. \(\begin{cases} 20x+5y=120\\ 10x+7.5y=80\end{cases}\) F. \(\begin{cases} 6x-2y=11\\ -9x+3y=16\end{cases}\)

G. \(\begin{cases} 2x-3y=-1\\ 3x+4y=8\end{cases}\) H. \(\begin{cases} 5x-2y=-19\\ 2x+3y=0\end{cases}\) I. \(\begin{cases} r+3s=7\\ 2r-s=7\end{cases}\)

练习： 解三元一次线性方程组

A.\(\begin{cases}2y-3z=0\\ x+3y=-4\\ 3x+4y=3\end{cases}\) B.\(\begin{cases}3x+y-2z=22\\ x+5y+z=4\\ x=-3z\end{cases}\) C.\(\begin{cases}2x-y+z=-2\\ x+3y-z=10\\ x+2z=-8\end{cases}\)

练习： 解三元一次线性方程组

A.\(\begin{cases}x-y+z=-1\\ x+y+3z=-3\\ 2x-y+2z=0\end{cases}\) B.\(\begin{cases}x-y-2z=4\\ -x+2y+z=1\\ -x+y-3z=11\end{cases}\) C.\(\begin{cases}-2x+y-z=2\\ -x-3y+z=-10\\ 3x+6z=-24\end{cases}\)

练习： 解三元一次线性方程组

A.\(\begin{cases}x-3y+2z=11\\ -x+4y+3z=5\\ 2x-2y-4z=2\end{cases}\) B.\(\begin{cases}x+2y+z=4\\ 2x-y+4z=-8\\ -3x+y-2z=-1\end{cases}\) C.\(\begin{cases}4x-y+2z=-6\\ -2x+3y-z=8\\ 2y+3z=-5\end{cases}\)

练习： 解三元一次线性方程组

A.\(\begin{cases}4x-2y+5z=6\\ 3x+3y+8z=4\\ x-5y-3z=5\end{cases}\) B.\(\begin{cases}4y+2x=6-3z\\ x+z-2y=-5\\ x-2z=3y-7\end{cases}\) C.\(\begin{cases}4x-y+z=-5\\ -x+y-z=5\\ 2x-z-1=y\end{cases}\)

练习： 解四元一次线性方程组

A.\(\begin{cases}-2w+x+y=0\\ -w+2x-y+z=1\\ -2w+3x+3y+2z=6\\ w+x+2y+z=5\end{cases}\) B.\(\begin{cases}2w+3x+y-z=7\\ 3w+x-2y+2z=7\\ w+2x+4y-2z=5\\ 2w+4x+2y+3z=18\end{cases}\)