中考几何压轴题目分析
北京.2018.27(明示旋转关系)
示例: 如图,在正方形 \(ABCD\) 中,\(E\) 是边 \(AB\) 上的一动点(不与点 \(A\) , \(B\) 重合),连接 \(DE\) ,点 \(A\) 关于直线 \(DE\) 的对称点为 \(F\) ,连接 \(EF\) 并延长交 \(BC\) 于点 \(G\) ,连接 \(DG\) ,过点 \(E\) 作 \(EH\perp DE\) 交 \(DG\) 的延长线于点 \(H\) ,连接 \(BH\) 。
(1)求证:\(GF=GC\);
(2)用等式表示线段 \(BH\) 与 \(AE\) 的熟练关系,并证明。
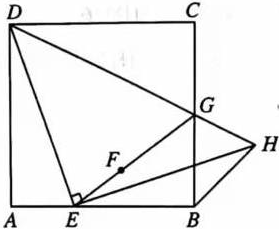
分析 (1)本题考查由轴对称产生的全等三角形,依次证明 \(\triangle{DAE}\cong\triangle{DFE}\) 与 \(\triangle{EFG}\cong\triangle{DCG}\) 即可。
(2)由(1)中分析易知 \(\triangle{DEG}\) 是由 \(\triangle{DAB}\) 相似旋转而来。而 \(AE\) 与 \(BH\) 是两个旋转顶点的轨迹。根据旋转相似模型,只需要证明 \(\triangle{DAE}\sim\triangle{DBH}\) ,再考查其相似比即可。
思考与讨论
本题所处中考年代的考试难度相对较低,优等生数学考个满分不是很难的事情。本题解法很多,在左下或右下添加辅助线构建全等三角形也是常见思路。请读者自行思考这些解法。
北京.2019.27(对称性)
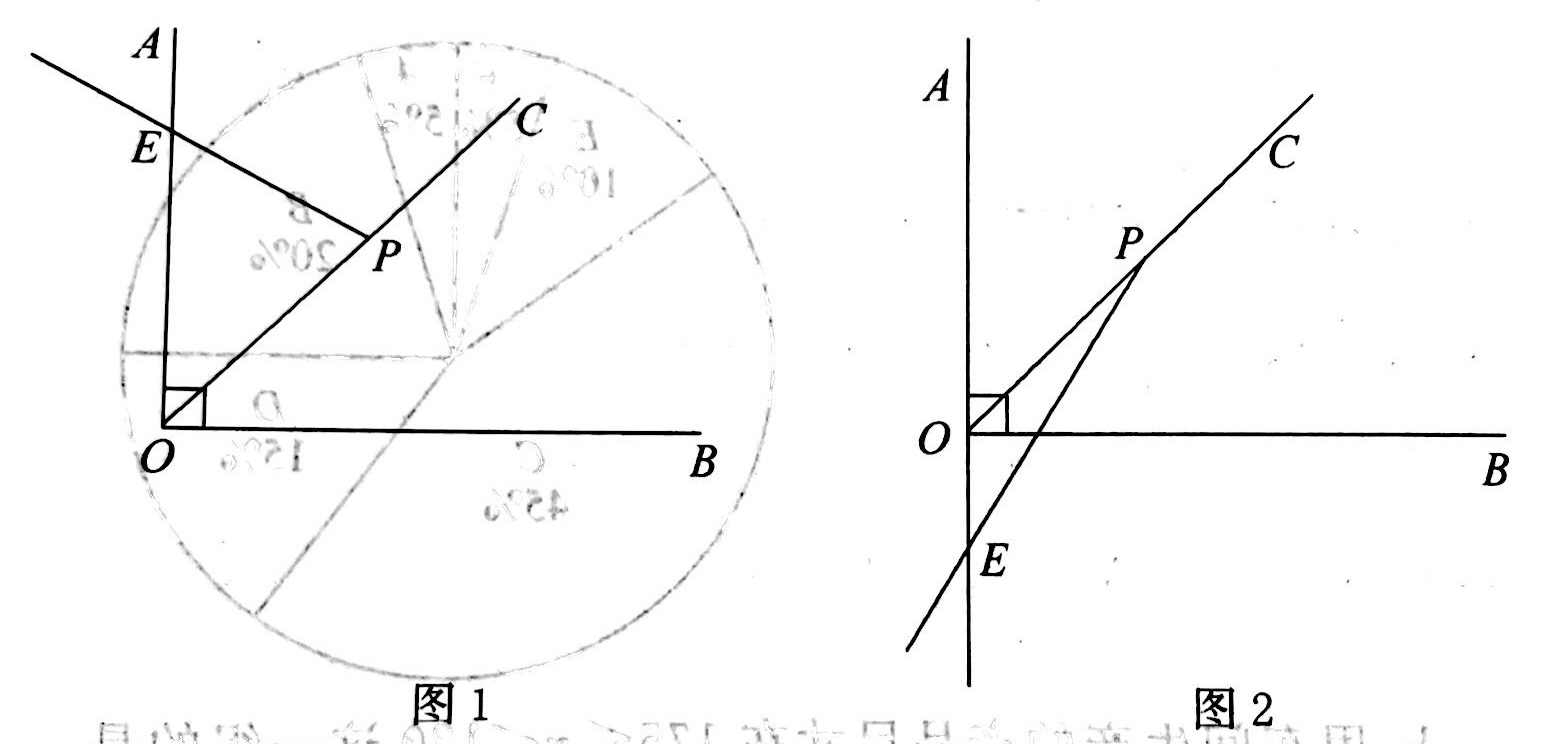
示例: 已知 \(\angle{AOB}=30^\circ\) ,\(H\) 为射线 \(OA\) 上一定点,\(OH=\sqrt{3}+1\) , \(P\) 为射线 \(OB\) 上一点, \(M\) 为线段 \(OH\) 上一动点,连接 \(PM\) ,满足 \(\angle{OMP}\) 为钝角,以点 \(P\) 为中心,将线段 \(PM\) 顺时针旋转 \(150^\circ\) ,得到线段 \(PN\) ,连接 \(ON\) 。
- [(1)] 依题意补全图 1;
- [(2)] 求证:\(\angle{OMP}=\angle{OPN}\) ;
- [(3)] 点 \(M\) 关于点 \(H\) 的对称点为 \(Q\) ,连接 \(QP\) ,写出一个 \(OP\) 的值,使得对于任意的点总有 \(ON=QP\) ,并证明。
北京.2020/22.27(对称性带来全等)
示例: 在 \(\triangle{ABC}\) 中,\(\angle{C}=90^\circ\),\(AC>BC\) , \(D\) 是 \(AB\) 的中点, \(E\) 为直线 \(AC\) 上一动点,连接 \(DE\) ,过点 \(D\) 作 \(DF\perp DE\) ,交直线 \(BC\) 于点 \(F\) ,连接 \(EF\) 。
- [(1)] 如图 1 ,当 \(E\) 是线段 \(AC\) 的中点时,设 \(AE=a,\ BF=b\) ,求 \(EF\) 的长(用含 \(a,b\) 的式子表示);
- [(2)] 当点 \(E\) 在线段 \(CA\) 的延长线上时,依题意补全图 2 ,用等式表示线段 \(AE,\ EF,\ BF\) 之间的数量关系,并证明。
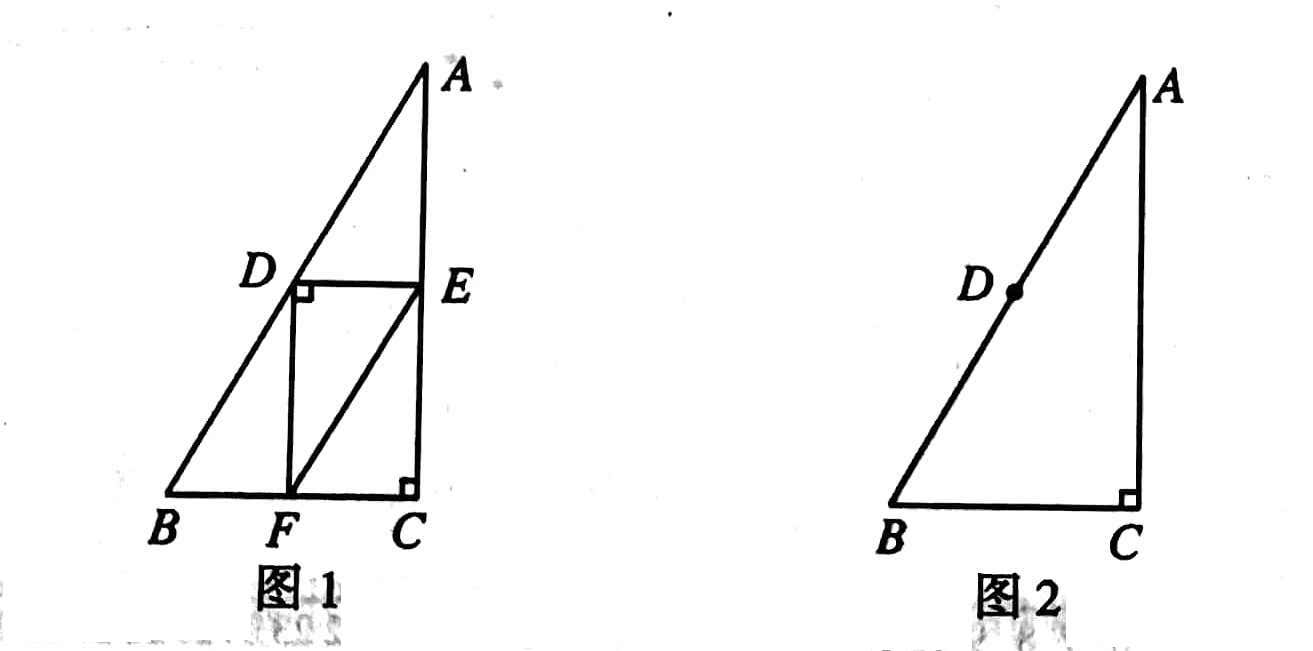
分析这里的全等由对称给出,在北京中考算放水了。
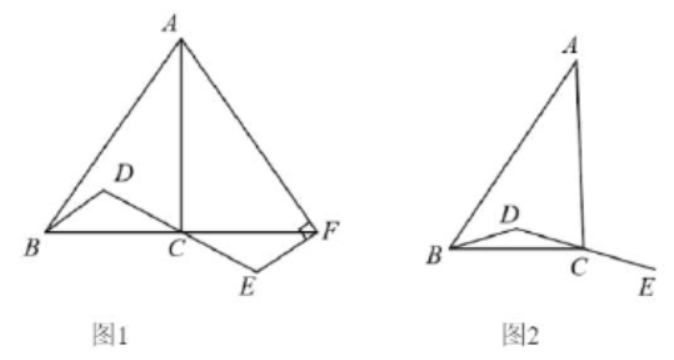
示例: (北京中考2022)在 \(\triangle{ABC}\) 中,\(\angle{ACB}=90^\circ\) , \(D\) 为 \(\triangle{ABC}\) 内一点,连接 \(BD\) ,\(DC\) ,延长 \(DC\) 到点 \(E\) ,使得 \(CE=DC\) 。
- [(1)] 如图 1,延长 \(BC\) 到点 \(F\) ,使得 \(CF=BC\) ,连接 \(AF\) ,\(EF\) ,若 \(AF\perp EF\) ,求证:\(BD\perp AF\) ;
- [(2)] 连接 \(AE\) ,交 \(BD\) 的延长线于点 \(H\) ,连接 \(CH\) ,依题意补全图 2,若 \(AB^2=AE^2+BD^2\) ,用等式表示线段 \(CD\) 与 \(CH\) 的数量关系,并证明。
北京.2021.27(轨迹角度判定)
示例: 如图 6 所示,在 \(\triangle{ABC}\) 中, \(AB=AC\) ,\(\angle{BAC}=\alpha\) ,\(M\) 为 \(BC\) 中点,点 \(D\) 在 \(MC\) 上,以点 \(A\) 为中心,将线段 \(AD\) 顺时针旋转 \(\alpha\) 得到线段 \(AE\) ,连接 \(BE,DE\) 。
(1)比较 \(\angle{BAE}\) 与 \(\angle{CAD}\) 的大小;用等式表示 \(BE,BM,MD\) 之间的数量关系,并证明。
(2)过点 \(M\) 做 \(AB\) 的垂线,交 \(DE\) 于点 \(N\) ,用等式表示线段 \(NE\) 与 \(ND\) 的数量关系,并证明。
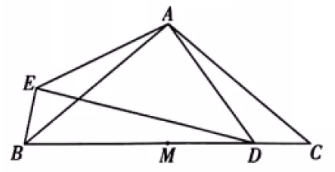
分析(1)显然 \(\triangle{ABC}\) 顺时针相似旋转至 \(\triangle{AED}\) ,所关心的两个角正好是轨迹对旋转中心的夹角,相等。
(2)考查题目中给出的垂线,其与直线 \(CB\) 成的角度恰好等于 \(CM\) 对旋转中心的夹角 \(\triangle{CAM}\)。所以 \(N\) 正好是 \(\triangle{AED}\) 在 \(\triangle{ABC}\) 上点 \(M\) 的相似对应点。所以容易得到 \(NE=ND\) 。
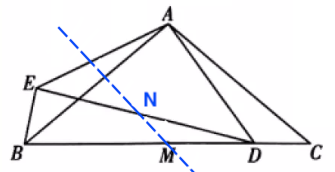
如何构建完整的证明呢?可以直接取 \(DE\) 的中点 \(N\),证明轨迹张成相似三角形 \(\triangle{ANM}\sim\triangle{ADC}\) ,然后证明轨迹 \(MN\) 垂直于 \(AB\) ,再根据交点的唯一性即可证明。
思考与讨论
2021年是一个特别的年份,在复杂的国际国内背景下,从这一年起,北京中考数学的压轴题开始变难。这道几何压轴题的得分率很低,出现了优等生大面积翻车的现象。如果直接看网上常见的解答,学习者会不知如何想到这种解法从而丧失学习信心。
北京.2023.27(轨迹角度长度判定)
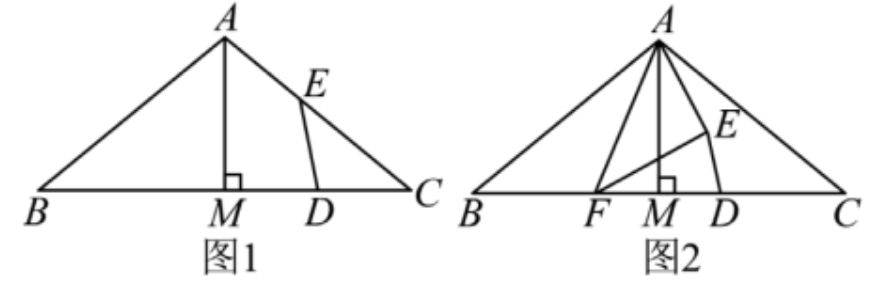
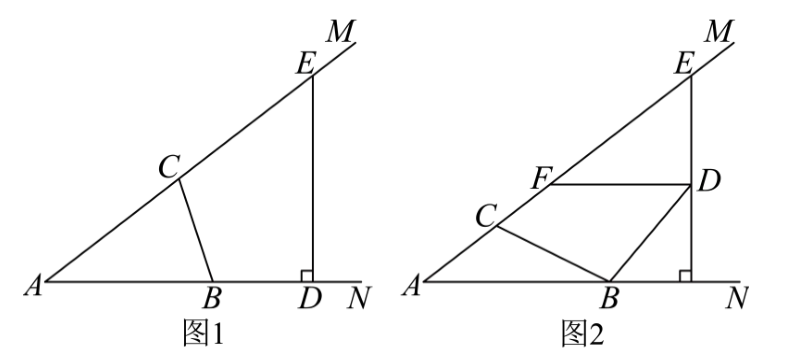
示例: (北京中考2023)在 \(\triangle{ABC}\) 中,\(\angle{B}=\angle{C}=\alpha(0^\circ<\alpha<45^\circ)\)。\(AM\perp BC\) 于点 \(M\) , \(D\) 是线段 \(MC\) 上的动点(不与点 \(M\) , \(C\) 重合),将线段 \(DM\) 绕点 \(D\) 顺时针旋转 \(2\alpha\) 得到线段 \(DE\) 。
(1)如图 1,当点 \(E\) 在线段 \(AC\) 上时,求证:\(D\) 是 \(MC\) 中点;
(2)如图 2,若在线段 \(BM\) 上存在点 \(F\) (不与点 \(B\),\(M\) 重合)满足 \(DF=DC\) ,连接 \(AE\) , \(EF\) ,直接写出 \(\angle{AEF}\) 的大小,并证明。
分析
(1)只要把已知角在图上标注出来,稍微追一下角,就可以发现 \(\triangle{CDE}\) 为等腰三角形,于是命题轻松得证。
(2)看出来\(\triangle{AEF}=90^\circ\) ,以及 \(\triangle{ABM}\sim\triangle{AFE}\) ,但是我们如何求证这一点呢?
在本问题中,似乎直接计算\(\triangle{ABM}\)与\(\triangle{AFE}\)角和边的关系不容易(这正是本题的难点所在)。于是我们转而考虑三角形两个运动顶点的轨迹关系,即考查线段 \(BF\) 和 \(ME\) 的关系。
如果是旋转相似模型,那么这两条轨迹的夹角(\(\angle{DME}\))应该等于两个旋转点对旋转中心张成的角,即 \(\angle{BAM}=90^\circ-\alpha\) 。此处正好将 \(2\alpha\) 的条件用上轻松证明。
旋转相似模型还要求轨迹的长度之比等于两个旋转点到旋转中心的距离,即 \(BF:ME=BA:MA\) 。注意到 \[MD=MC-CD=\dfrac{1}{2}(BC-FC)=\dfrac{1}{2}BF\] (此处利用了 \(FD=DC\) 条件),再利用 \(2\alpha\) 条件计算 \(ME\) 的长度,发现正好能够验证 \(BF:ME=BA:MA\) 比例要求。
重构整个证明过程时,直接证明轨迹对旋转中心张成相似三角形,即:\(\triangle{BFA}\sim\triangle{MEA}\) ,于是问题变迎刃而解。
北京.2024.27(判定轨迹的角度)
示例: (北京中考2024)已知 \(\angle{MAN}=\alpha(0^\circ<\alpha<45^\circ)\) ,点 \(B\),\(C\) 分别在射线 \(AN\),\(AM\) 上,将线段 \(BC\) 绕点 \(B\) 顺时针旋转 \(180^\circ-2\alpha\) 得到线段 \(BD\) ,过点 \(D\) 作 \(AN\) 的垂线交射线 \(AM\) 于点 \(E\) 。
(1)如图 1,当点 \(D\) 在射线 \(AN\) 上时,求证: \(C\) 是 \(AE\) 中点;
(2)如图 2,当点 \(D\) 在 \(\angle{MAN}\) 内部时,作 \(DF\parallel AN\) ,交射线 \(AM\) 于点 \(F\) ,用等式表示线段 \(EF\) 与 \(AC\) 的数量关系,并证明。
分析
定住 \(C\) 的位置,移动点 \(B\) ,则 \(\triangle{CDE}\) 在进行连续旋转相似变换。可以得到 \(D\) 的轨迹为平行于 \(AM\) 的直线,于是 \(EF\) 为定长。剩下的事情就很简单了,找个特殊位置(例如 \(CD\) 处于水平位置)计算 \(EF\) 长度即可。
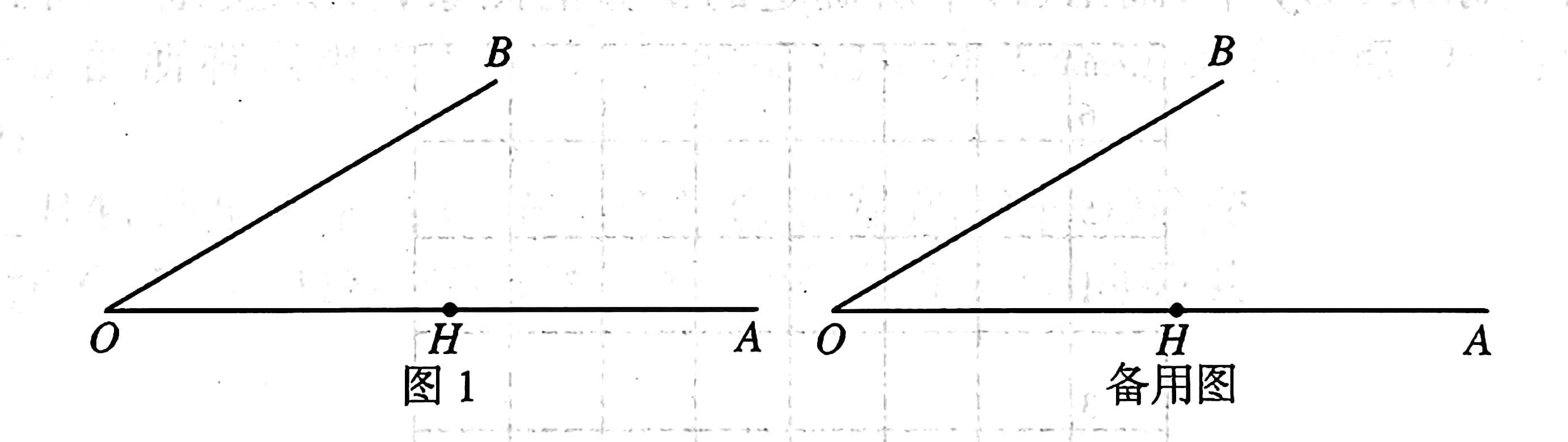
北京.2019 各区模拟题
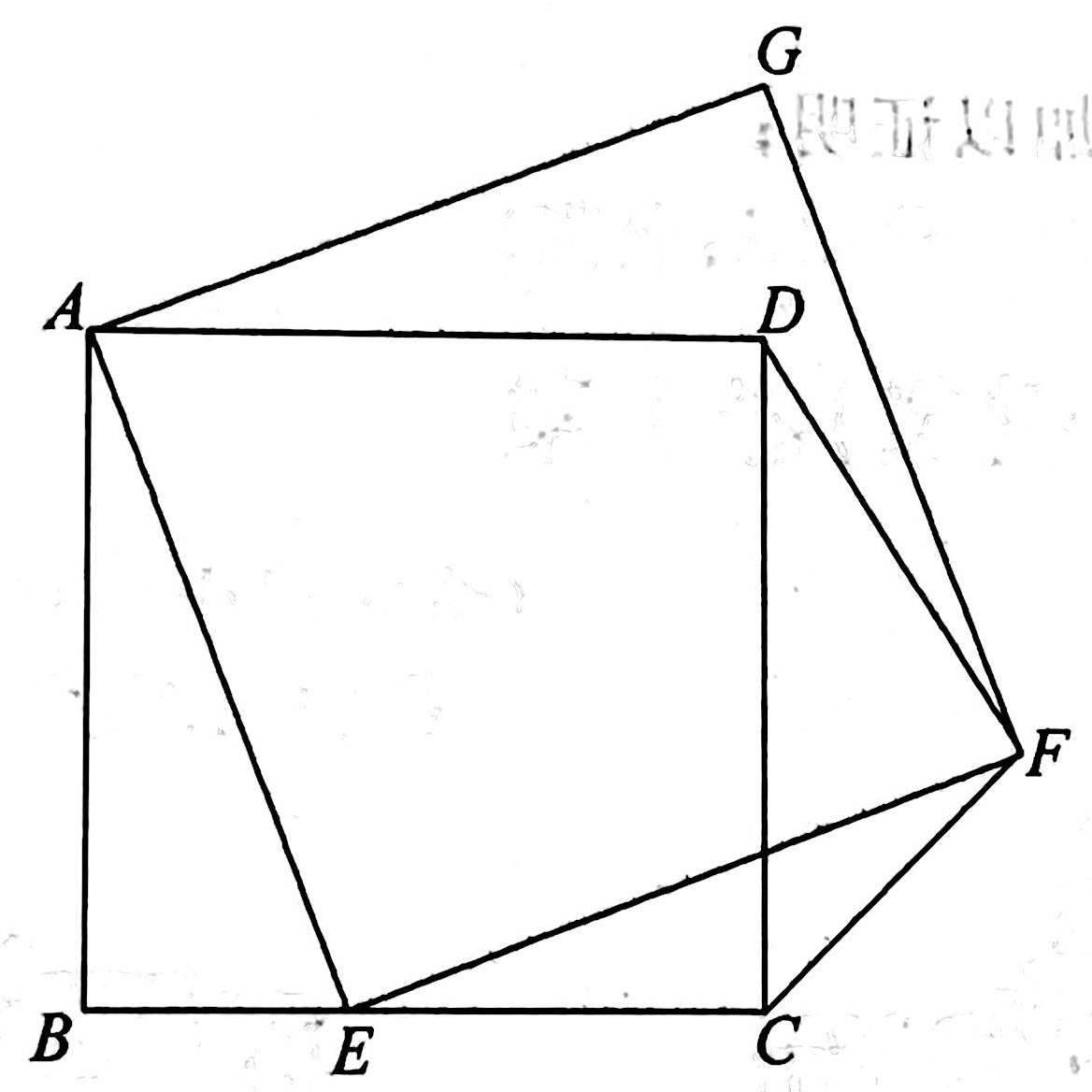
示例: 在正方形 \(ABCD\) 中,点 \(E\) 为 \(BC\) 边上一动点,连接 \(AE\) ,以 \(AF\) 为边,在线段 \(AE\) 右侧作正方形 \(AEFG\) ,连接 \(CF\) , \(DF\) 。
(1)求 \(CF\) 和 \(BE\) 的数量关系。
(2)求 \(DF\) 和 \(BE\) 的函数关系。
北京市中考(暗示旋转关系)
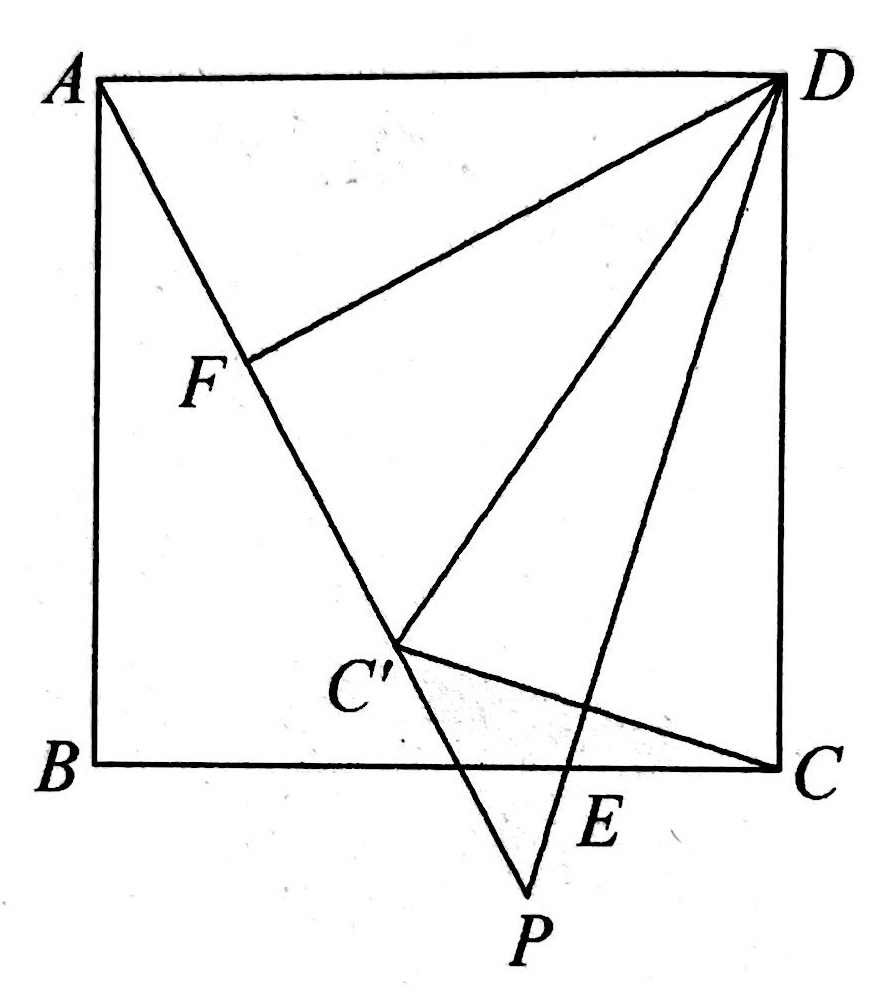
示例: 如图 10 所示,在正方形 \(ABCD\) 中, \(E\) 是边 \(BC\) 上一动点(不与点 \(B,C\) 重合),连接 \(DE\) ,点 \(C\) 关于直线 \(DE\) 的对称点为 \(C'\) ,连接\(AC'\)并延长直线\(DE\)于点 \(P\) , \(F\) 是 \(AC'\) 中点,连接 \(DF\) 。
(1)求 \(\angle{FDP}\) 的度数。
(2)连接 \(BP\) ,请用等式表示 \(AP,BP,DP\) 三条线段之间的数量关系,并证明。
(3)连接 \(AC\) ,若正方形的边长为 \(\sqrt{2}\) ,请直接写出 \(\angle{ACC'}\) 的面积最大值。
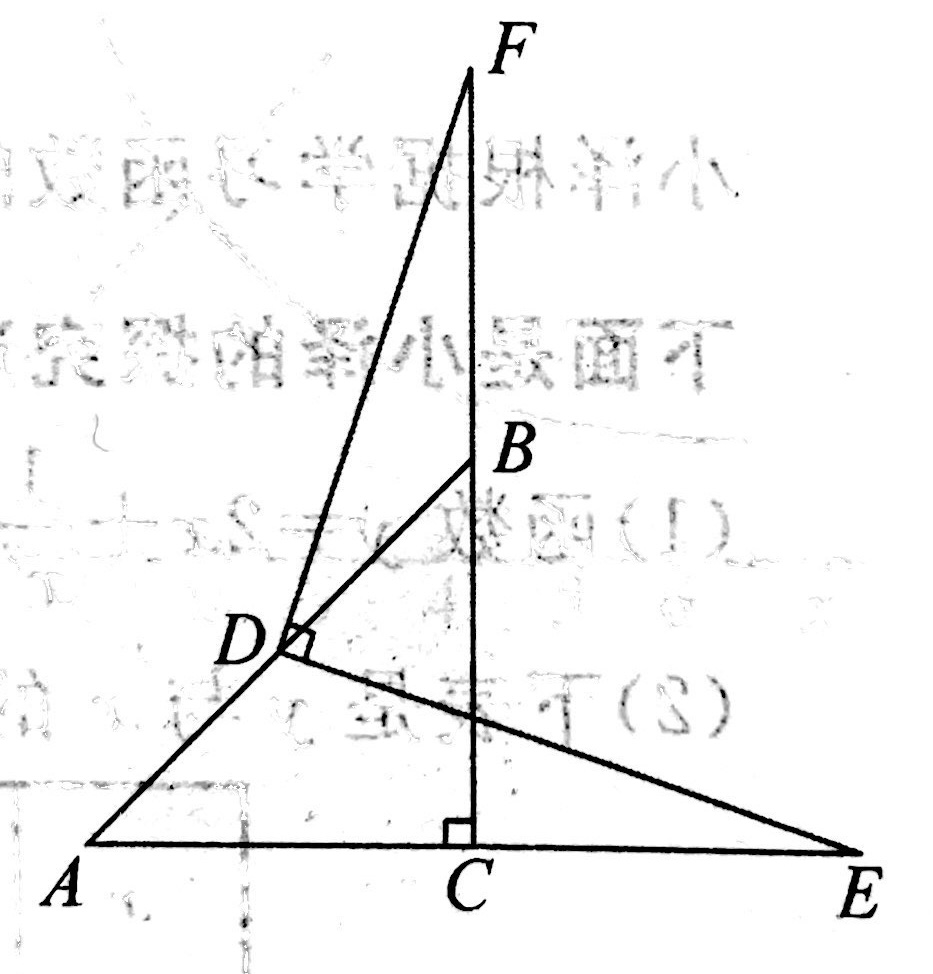
示例: 如图 11 所示,在 \(\triangle{ABC}\) 中, \(\triangle{ACB}=90^\circ\), \(AC=BC\) , \(D\) 为 \(AB\) 的中点,点 \(E\) 为 \(AC\) 延长线上一点,连接 \(DE\) ,过点 \(D\) 作 \(DF\perp DE\) 交 \(CB\) 的延长线于点 \(F\) 。
(1)求证: \(BF=CE\) 。
(2)若 \(CE=AC\) ,用等式表示线段 \(DF\) 与 \(AB\) 的数量关系,并证明。
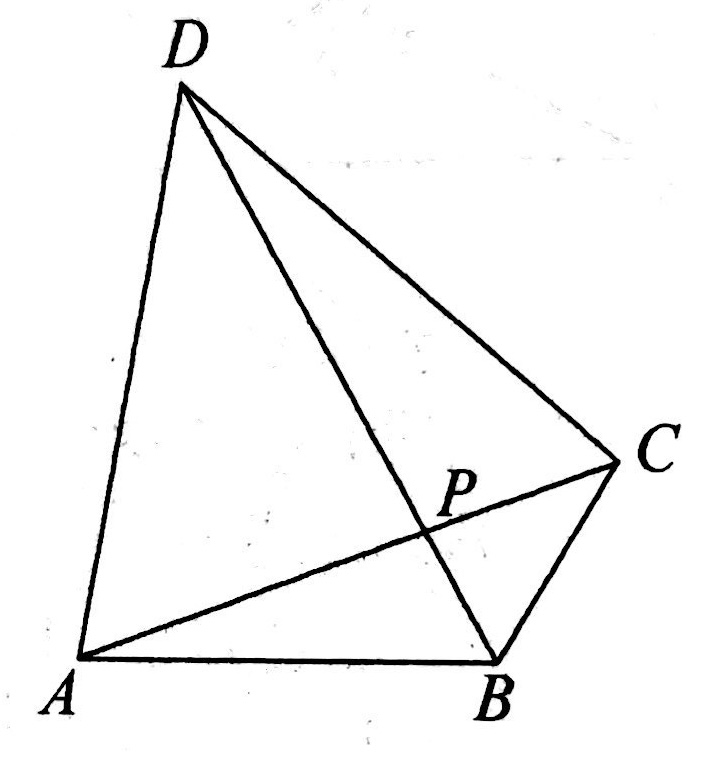
示例: 在 \(\triangle{ABC}\) 中,线段 \(AC\) 绕点 \(A\) 逆时针旋转 \(60^\circ\) 得到线段 \(AD\) ,连接 \(CD\) ,\(BD\) 交 \(AC\) 于点 \(P\) 。
(1)若 \(\angle{BAC}=\alpha\) ,直接写出 \(\angle{BCD}\) 的度数是 \(\_\_\_\_\_\_\) (用含 \(\alpha\) 的代数式表示);
(2)求 \(AB\) , \(BC\) , \(BD\) 之间的数量关系;
(3)当 \(\alpha=30^\circ\) 时,直接写出 \(AC\) , \(BD\) 的关系。
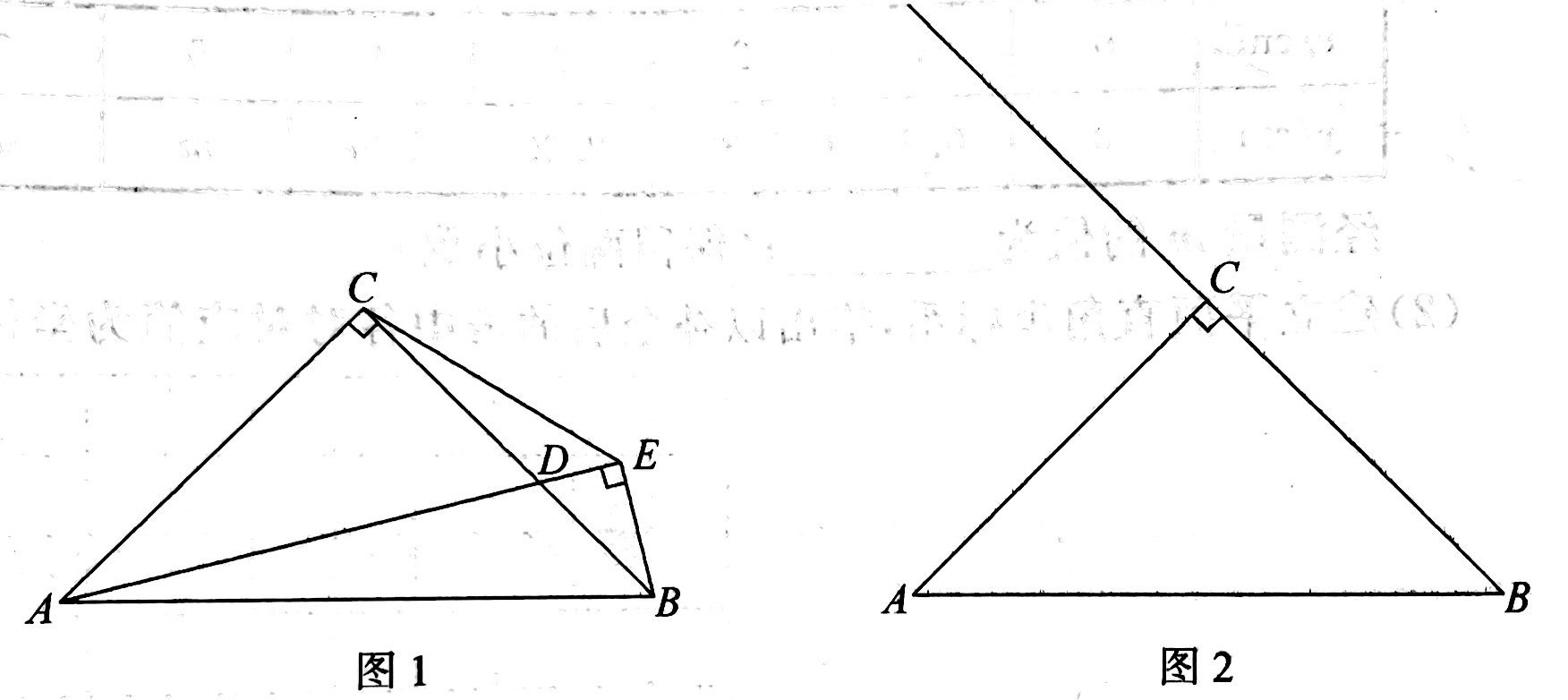
示例: 已知: \(Rt\triangle{ABC}\) 中,\(\angle{ACB}=90^\circ\) , \(AC=BC\) 。
(1)如图 1 ,点 \(D\) 是 \(BC\) 边上一点(不与点 \(B\) , \(C\) 重合),连接 \(AD\) ,过点 \(B\) 作 \(BE\perp AD\) ,交 \(AD\) 的延长线于点 \(E\) ,连接 \(CE\) 。若 \(\angle{BAD}=\alpha\) ,求 \(\angle{DBE}\) 的大小(用含 \(\alpha\) 的式子表示);
(2)如图 2 ,点 \(D\) 在线段 \(BC\) 的延长线上时,连接 \(AD\) ,过点 \(B\) 作 \(BE\perp AD\) ,垂足 \(E\) 在线段 \(AD\) 上,连接 \(CE\) 。 依题意补全图 2;用等式表示线段 \(EA\) , \(EB\) 和 \(EC\) 之间的数量关系,并证明。
示例: 在 \(Rt\triangle{ABC}\) 中,\(\angle{ACB}=90^\circ\) , \(CA=CB\) 。点 \(D\) 为线段 \(BC\) 上一个动点(点 \(D\) 不与点 \(B\) ,\(C\) 重合),连接 \(AD\) ,点 \(E\) 在射线 \(AB\) 上,连接 \(DE\) ,使得 \(DE=DA\) 。作点 \(E\) 关于直线 \(BC\) 的对称点 \(F\) ,连接 \(BF\) , \(DF\) 。
(1)依题意补全图形;
(2)求证: \(\angle{CAD}=\angle{BDF}\) ;
(3)用等式表示线段\(AB\),\(BD\),\(BF\)之间的数量关系,并证明。

示例: 如图, \(\angle{AOB}=90^\circ\) , \(OC\) 为 \(\angle{AOB}\) 的平分线,点 \(P\) 为 \(OC\) 上一个动点,过点 \(P\) 作射线 \(PE\) 交 \(OA\) 于点 \(E\) 。以点 \(P\) 为旋转中心,将射线 \(PE\) 沿逆时针方向旋转 \(90^\circ\) ,交 \(OB\) 于点 \(F\) 。
(1)依题意补全图 1 ,并证明 \(PE=PF\);
(2)如图 1 ,如果点 \(E\) 在 \(OA\) 边上,用等式表示线段 \(OE\) , \(OP\) 和 \(OF\) 之间的数量关系,并证明;
(3)如图 2 ,如果点 \(E\) 在 \(OA\) 边的反向延长线上,直接写出线段 \(OE\) , \(OP\) 和 \(OF\) 之间的数量关系。