全等三角形

全等三角形的判定 (SAS)

定理：如果两个三角形中，一个的两边分别等于另一个两边，且相等线段所夹的角相等。那么他们的底边相等，两个三角形全等，且其余的角也分别等于相应的角，即等边所对的角。 (Euclid I.4)

全等三角形的判定 (SSS)

定理：如果一个三角形的三条边与另外一个三角形的三条边都相等，那么等边所夹的角也都相等。 (Euclid I.8)

全等三角形的判定 (ASA)

定理：如果两个三角形中，一个的两角分别等于另一个两角，且相等两角所夹的边相等。那么两个三角形全等。

\(\triangle{ABC} \cong \triangle{A‘B’C‘}\)

全等三角形的符号

如果 \(\triangle{ABC}\) 与 \(\triangle{A‘B’C‘}\) 全等，记作 \(\triangle{ABC} \cong \triangle{A‘B’C‘}\) 。注意，字母的排列次序应当和三角形的边角相等的对应次序一样，即应当有 \(AB=A'B',BC=B'C',CA=C'A'\) 。

全等三角形的判定：边角边（左）、边边边（中）、角边角（右）

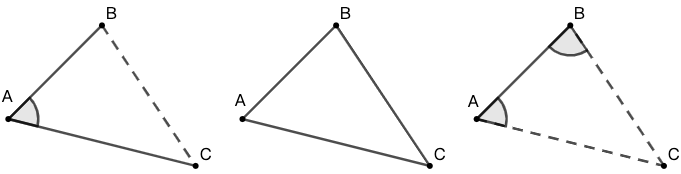
思考与讨论

初学者常常误用“边边角”进行全等三角形判定。即在 \(\triangle{ABC}\) 与 \(\triangle{A'B'C'}\) 中， \(AB=A'B'\)，\(BC=B'C'\)，\(\angle{C}=\angle{C'}\) 就得出三角形全等的结论。这是不对的，你能画图说明为什么这种判定方法不对么？
你如何证明上述全等三角形判定定理？请注意，这些判定是非常基本的定理，你无法使用更“高级”的结论来证明这些定理。在你的证明过程中，你使用了哪些公理、公设或定理呢？审视一下你的证明是不是构建在更为基本的命题上。

全等三角形的判定定理是非常基础的定理，有许多其它结论都是从全等三角形导出。下面让我们用其来证明角平分线作图的正确性。

示例：（Euclid I.9）证明角平分线的作图成立。

角平分线作图

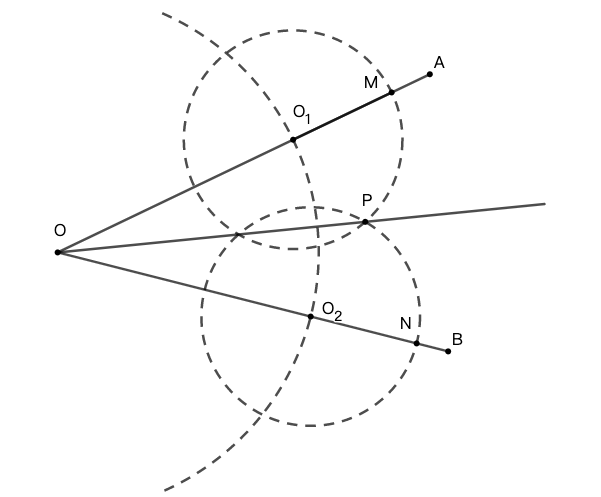
证明这是典型的利用全等三角形证明的命题。证明 \(\triangle{OO_1P}\) 和 \(\triangle{OO_2P}\) 全等，从而得到 \(\angle{O_1OP}=\angle{O_2OP}\) 。证明步骤如下：

由于点 \(O_1\) 和 \(O_2\) 在圆 \(O\) 上，所以 \(OO_1=OO_2\) 。（圆的定义）
由于圆 \(O_1\) 和圆 \(O_2\) 半径相同，所以 \(O_1P=O_2P\) 。（圆的定义）
在 \(\triangle{OO_1P}\) 和 \(\triangle{OO_2P}\) 中 \(OP=OP, OO_1=OO_2, O_1P=O_2P\) ，因此 \(\triangle{OO_1P} \cong \triangle{OO_2P}\) （三角形全等判定定理(SSS)）
因此 \(\angle{O_1OP}=\angle{O_2OP}\) ，证毕。（全等三角形对应角相等）

☐

思考与讨论

证明等腰三角形的两底角相等(Euclid I.5)。请列出你使用了哪些更基本的命题，这些命题可以由公理和定义导出么？
你要从等腰三角形的定义（两边相等）出发，证明这两条腰所对的角相等。
你不必按照欧几里得在《几何原本》中给出的证明，但要谨慎地检查你的结论能否从最基本的定义和公理导出。
证明上述命题的逆命题(Euclid I.6)。

平行四边形

平行四边形 (Parallelogram) 的定义

定义：两组对边分别平行的四边形叫做平行四边形。

小学课内教学中，在“认识图形”时，平行四边形的定义和性质是一同介绍的。但单独从字面上看，“平行四边形”只包含了“对边平行”，其它性质诸如对边对角相等、中心对称等性质，需要从定义中证明出来。下面给出了平行四边形边角的重要性质，其证明留作习题。（你也可以扫描右边的二维码观看相关讲解）

平行四边形的对边对角关系

定理：四边形如果由两条对边平行且相等，则另一组对边也平行且相等。(Euclid I.33)

定理：四边形的两组对边分别平行（平行四边形），则对边对角彼此相等，且对角线二等分该四边形。(Euclid I.34)

平行四边形的性质是“很好的性质”，具体地说就是这些性质的逆命题都成立。例如，平行四边形的对角相等，（逆命题）对角相等的四边形是平行四边形。再比如，平行四边形的对边相等，（逆命题）对边相等的四边形是平行四边形。

习惯上使用“反之亦然”(“and vice versa”)表示命题的逆命题成立。例如：“平行四边形的对角相等，反之亦然”。

平行四边形的面积

定理：同底且在相同平行线之间的平行四边形彼此面积相等。(Euclid I.35)

上述定理保证了平行四边形的面积等于底乘以高，即在两平行线之间同底的矩形的面积。如果平行四边形的底长度为 \(b\) ，高为 \(h\) ，则平行四边形的面积 \(S\) 的计算方法为 \(S=b\cdot h\) 。

平行四边形面积性质的证明

示例： (Euclid I.35) 在图 3 中， \(AF\parallel BC\) ，求证四边形 \(ABCD\) 和 \(CBEF\) 面积相同。

证明 (1) \(AD=BC=EF\) （平行四边形对边相等）

\(AE=AD+DE=DE+EF=DF\) （等量加等量，其和仍相等）
\(\angle{BAE}=\angle{CDF},\angle{AEB}=\angle{DFC}\) （同位角相等）
\(\triangle{ABE}\cong\triangle{DCF}\) （全等三角形判定(ASA)）
\(S_{ABCD}=S_{\triangle{ABE}}-S_{\triangle{GDE}}-S_{\triangle{GBC}}\)

\(S_{CBEF}=S_{\triangle{DCF}}-S_{\triangle{GDE}}-S_{\triangle{GBC}}\)

综上所述， \(S_{ABCD}=S_{CBEF}\) 。

☐

全等三角形（北京中考真题）

示例：（2014 北京）如图 4 所示，点 \(B\) 在线段 \(AD\) 上，\(BC\parallel DE\) ， \(AB=ED\) ， \(BC=DB\)。求证： \(\angle{A}=\angle{E}\) 。

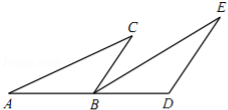
示例：（2013 北京）如图 5 所示， \(D\) 是 \(AC\) 上一点， \(AB=DA\) ， \(DE\parallel AB\) ， \(\angle{B}=\angle{DAE}\) 。求证： \(BC=AE\) 。

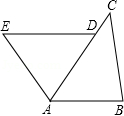
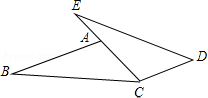
示例：（2012 北京）如图，点 \(E,A,C\) 在同一直线上， \(AB\parallel CD\)，\(AB=CE\)，\(AC=CD\) 。求证： \(BC=ED\) 。

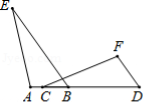
示例：（2011 北京）如图 7 所示，点 \(A\)、\(B\)、\(C\)、\(D\)在同一条直线上，\(BE\parallel DF\)，\(\angle{A}=\angle{F}\)，\(AB=FD\)。求证：\(AE=FC\) 。

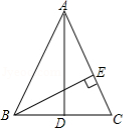
示例：（2015 北京）如图 8 所示，在 \(\triangle{ABC}\) 中， \(AB=AC\) ， \(AD\) 是 \(BC\) 边上的中线， \(BE\perp AC\)于点 \(E\) 。求证：\(\angle{CBE}=\triangle{BAD}\) 。

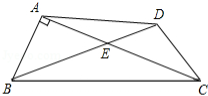
示例：（2013 北京）如图 9 所示，在四边形 \(ABCD\) 中，对角线 \(AC\) ，\(BD\) 交于点 \(E\)，\(\angle{BAC}=90^\circ\) ， \(\angle{CED}=45^\circ\) ， \(\angle{DCE}=30^\circ\) ，\(DE=\sqrt{2}\) ， \(BE=2\sqrt{2}\) ．求 \(CD\) 的长和四边形 \(ABCD\) 的面积。

示例：（2013 北京）如图 10 所示，在\(\triangle{ABC}\)中，\(AB=AC\)，\(\triangle{BAC}=\alpha\) , \(0^\circ<\alpha<60^\circ\) ，将线段 \(BC\) 绕点 \(B\) 逆时针旋转 \(60^\circ\) 得到线段 \(BD\) 。

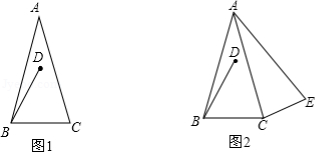
（1）如图 \(1\) ，直接写出 \(\triangle{ABD}\) 的大小（用含 \(\alpha\) 的式子表示）；

（2）如图 \(2\) ，\(\triangle{BCE}=150^\circ\) ，\(\triangle{ABE}=60^\circ\) ，判断 \(\triangle{ABE}\) 的形状并加以证明；

（3）在（2）的条件下，连接 \(DE\) ，若 \(\triangle{DEC}=45^\circ\) ，求 \(\alpha\) 的值。