平面向量初步

向量的加法和数乘

在本讲义中，我们只讨论实向量

向量的定义和表示

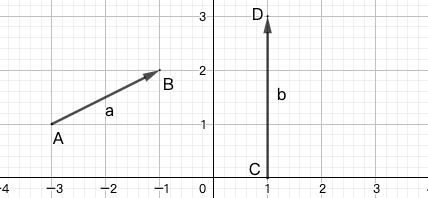
向量（也称为矢量）是具有大小和方向的量。使用起点和终点再加上箭头表示向量。如 1 中的 \(\overrightarrow{AB}\) 和 \(\overrightarrow{CD}\) 。也可以使用带箭头的小写字表示向量，如 \(\vec{a}\) 和 \(\vec{b}\) 。在印刷体中，有时也使用加粗的小写字母表示向量，如 \(\mathbf{a}\) 或 \(\mathbf{b}\) 。

平面向量是在二维平面内的向量。在平面直角坐标系中，使用向量在 \(x\) 轴和 \(y\) 轴的投影的有向距离（分正负）表示向量，如图 1 中： \[\overrightarrow{AB}=\begin{bmatrix} 2\\1 \end{bmatrix}\quad \overrightarrow{CD}=\begin{bmatrix} 0\\3 \end{bmatrix}\]

向量

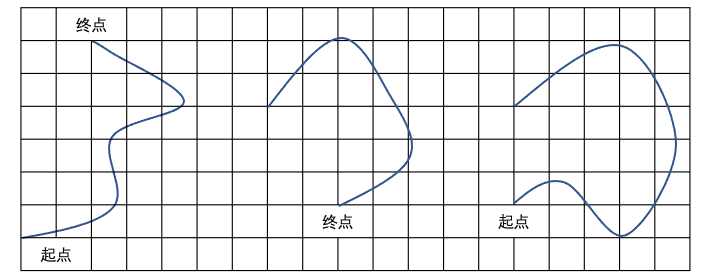
示例：位移是从路径起点指向路径终点的向量。位移与路径的具体细节无关。请画出图 2 中的位移向量，并用数值表示。

向量

向量的模

向量的长度也称为向量的模，用符号记为 \(|\overrightarrow{AB}|\) 或 \(|\mathbf{a}|\) 。

起点和终点相同的向量称为零向量，记作 \(\vec{0}\) ，印刷也用粗体 \(\mathbf{0}\) 表示。零向量的模是 \(0\) 。

模等于 \(1\) 的向量称为单位向量，常用小写字母 \(\mathbf{e}\) 表示。

在平面直角坐标系中，向量 \(\begin{bmatrix} x\\y \end{bmatrix}\) 的模等于 \(\sqrt{x^2+y^2}\) 。

示例：计算向量 \(\vec{a}=\begin{bmatrix} 3\\4 \end{bmatrix}\) 的模。

解： \(|\vec{a}|=\sqrt{3^2+4^2}=5\)

☐

示例：计算向量 \(\vec{a}=\begin{bmatrix} -3\\-4 \end{bmatrix}\) 的模。

解： \(|\vec{a}|=\sqrt{(-3)^2+(-4)^2}=5\)

☐

示例：在平面直角坐标系中，点 \(X\) 的坐标为 \((5,5)\) ，点 \(Y\) 的坐标为 \(2,1\) ，画出 \(\overrightarrow{XY}\) ，并求 \(|\overrightarrow{XY}|\) 。

示例：在平面直角坐标系中，点 \(A\) 的坐标为 \((-3,2)\) ，点 \(Y\) 的坐标为 \(2,-3\) ，画出 \(\overrightarrow{XY}\) ，并求 \(|\overrightarrow{XY}|\) 。

向量的加法

将两个向量首尾相连，从起点指向终点的向量就是两个向量的和（如图 3 所示。）。这称为向量相加的三角形法则。

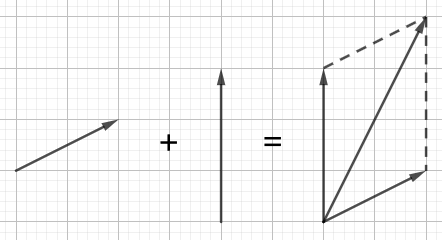
将两个向量的起点放置于同一点，张成平行四边形，起点所在的对角线就是向量的和（如图 4 所示）。这称为向量相加的平行四边形法则。、

在直角坐标系的表示中，向量相加是非常容易的，只需要将向量在 \(x\) 方向和 \(y\) 方向的有向投影分别相加即可。即在图 3 中，向量的加法运算可以表示为： \[\begin{bmatrix} 2\\1 \end{bmatrix} + \begin{bmatrix} 0\\3 \end{bmatrix} = \begin{bmatrix} 2\\4 \end{bmatrix}\]

三角形法则

平行四边形法则

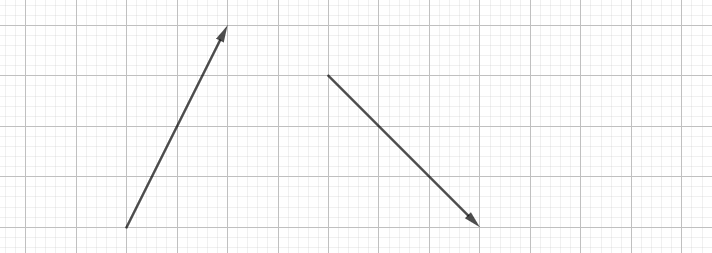
示例：使用三角形法则对图 5 中的向量求和，并写出直角坐标系的向量数值相加的算式。

平行四边形法则

容易验证，向量的加法满足结合律、交换律。向量的加法也具有封闭性，在二维（三维）空间内的两个向量之和仍然是二维（三维）空间内的向量。

向量加法的单位元是零向量，它与任何向量相加，都不改变该向量。每个向量针对加法运算都有唯一的逆元，长度相同方向相反的向量，向量与其逆元的和等于零向量。

思考与讨论

减法是加法的逆运算，如何定义向量的减法？
向量减法的几何意义是什么？
用平面直角坐标表示的向量，如何做减法？

向量的数乘

给定一个实数 \(\lambda\) 和向量 \(\mathbf{a}\) ，规定它们的乘积是一个向量，记作 \(\lambda\mathbf{a}\) 。当\(\lambda=0\) 或 \(\mathbf{a}=\mathbf{0}\) 时，\(\lambda\mathbf{a}=\mathbf{0}\) 。若二者均不为零，\(|\lambda\vec{a}|\) 的模规定为 \(|\lambda||\mathbf{a}|\) 。当 \(\lambda>0\) 时，\(\lambda\mathbf{a}\) 与 \(\mathbf{a}\) 的方向相同； \(\lambda<0\) 时， \(\lambda\mathbf{a}\) 与 \(\mathbf{a}\) 的方向相反。

示例： \(\mathbf{a}=\begin{bmatrix} -1\\2 \end{bmatrix}\) ，请在直角坐标系中绘制向量 \(2\mathbf{a}\) 和 \(-1.5\mathbf{a}\) 。

向量的线性运算

向量数乘和加法的分配律

向量的数乘和加法满足分配律，即：

对于任意实数 \(\lambda_1,\lambda_2\) 与任意向量 \(\mathbf{a}\) 有：\[\lambda_1\mathbf{a}+\lambda_2\mathbf{a}=(\lambda_1+\lambda_2)\mathbf{a}\]

对于任意实数 \(\lambda\) 与任意向量 \(\mathbf{a_1},\mathbf{a_2}\) 有：\[\lambda\mathbf{a_1}+\lambda\mathbf{a_2}=\lambda(\mathbf{a_1}+\mathbf{a_2})\]

向量的线性组合

对于向量 \(\mathbf{a_1},\mathbf{a_2}, ...,\mathbf{a_n}\) ，称 \(\lambda_1\mathbf{a_1}+\lambda_2\mathbf{a_2}+...+\lambda_n\mathbf{a_n}\) 是向量 \(\mathbf{a_1},\mathbf{a_2}, ...,\mathbf{a_n}\) 的一个线性组合。其中 \(\lambda_1,\lambda_2,...,\lambda_n\) 为实数。

示例：将向量 \(\begin{bmatrix} 3\\4 \end{bmatrix}\) 写成向量 \(\begin{bmatrix} 1\\2 \end{bmatrix}\) 和 \(\begin{bmatrix} 2\\1 \end{bmatrix}\) 的线性组合。

示例：将 \(\begin{bmatrix} 3\\4 \end{bmatrix}\) 写成向量 \(\begin{bmatrix} 1\\1 \end{bmatrix}\),\(\begin{bmatrix} 1\\2 \end{bmatrix}\) 和 \(\begin{bmatrix} 2\\1 \end{bmatrix}\) 的两种不同线性组合。

示例：证明，任意平面向量\(\begin{bmatrix} a\\b \end{bmatrix}\)都可以由 \(\begin{bmatrix} 1\\2 \end{bmatrix}\) 和 \(\begin{bmatrix} 2\\1 \end{bmatrix}\) 的线性组合得到。

线性相关与线性无关

对于向量\(\mathbf{a_1},\mathbf{a_2}, ...,\mathbf{a_n}\)，如果存在不全为\(0\)的实数\(\lambda_1,\lambda_2,...,\lambda_n\)，使得 \(\lambda_1\mathbf{a_1}+\lambda_2\mathbf{a_2}+...+\lambda_n\mathbf{a_n}=\mathbf{0}\) ，则称向量 \(\mathbf{a_1},\mathbf{a_2}, ...,\mathbf{a_n}\) 线性相关。否则（不存在这样的\(\lambda_1,\lambda_2,...,\lambda_n\)），则称 \(\mathbf{a_1},\mathbf{a_2}, ...,\mathbf{a_n}\) 线性无关。

示例：给定向量 \(\begin{bmatrix} 1\\2 \end{bmatrix}\) ，请再写出一个向量，让二者线性相关，并绘制在平面直角坐标系中。

示例：证明，任意三个平面向量线性相关。

对于二维平面向量来说，两个非零向量线性相关意味着它们方向相同或相反，称为平行或共线。

任意三个平面向量都是线性相关的。

平面向量基本定理

如果平面内两个向量 \(\mathbf{a}\) 和 \(\mathbf{b}\) 线性无关，则对平面内的任一向量 \(\mathbf{c}\) ，存在\(\mathbf{a},\mathbf{b}\) 的唯一线性组合使得：\[\mathbf{c}=\lambda\mathbf{a}+\beta\mathbf{b}\]

示例：判断向量 \(\begin{bmatrix} 1\\2\\3 \end{bmatrix}\) ，\(\begin{bmatrix} 3\\2\\2 \end{bmatrix}\) 和 \(\begin{bmatrix} 5\\2\\1 \end{bmatrix}\) 是否线性相关。

示例：判断向量 \(\begin{bmatrix} 1\\2\\3 \end{bmatrix}\) ，\(\begin{bmatrix} 3\\2\\2 \end{bmatrix}\) 和 \(\begin{bmatrix} 4\\2\\1 \end{bmatrix}\) 是否线性相关。

思考与讨论

上述问题中的向量称为三维向量，表示三维空间中有方向的量，请尝试在纸上绘制出来。
三维空间中，三个向量线性相关，对应的几何含义是什么？
三维空间中，任意四个向量线性相关么？如果是请尝试证明，不是请举出反例。

向量的内积

我们定义了向量的加法和数乘，向量之间能够做乘法么，答案是肯定的。两个向量的乘法与其夹角密切相关，我们先来定义向量的夹角：

给定两个非零向量 \(\mathbf{a},\mathbf{b}\) ，任选一点 \(O\) ，做 \(\overrightarrow{OA}=\mathbf{a},\overrightarrow{OB}=\mathbf{b}\) ，则称 \([0,\pi]\) 内的 \(\angle{AOB}\) 为向量 \(a\) 与 \(b\) 的夹角，记作 \(\langle\mathbf{a},\mathbf{b}\rangle\) 。

\(\langle\mathbf{a},\mathbf{b}\rangle=\dfrac{\pi}{2}\) 时，称 \(\mathbf{a}\) 与 \(\mathbf{b}\) 垂直，记作 \(\mathbf{a}\perp\mathbf{b}\) 。

由于零向量的方向是不确定的，在讨论垂直问题时，规定零向量垂直于任何向量。

向量的内积

定义非零向量 \(\mathbf{a}\) 与 \(\mathbf{b}\) 的内积为 \(|\mathbf{a}||\mathbf{b}|\cos\langle\mathbf{a},\mathbf{b}\rangle\) ，记作 \(\mathbf{a}\cdot \mathbf{b}\) 。即：\[\mathbf{a}\cdot\mathbf{b}=|\mathbf{a}||\mathbf{b}|cos\langle\mathbf{a},\mathbf{b}\rangle\]

向量内积的几何意义就是向量 \(\mathbf{a}\) 在向量 \(\mathbf{b}\) 上的投影的有向长度和向量 \(\mathbf{b}\) 长度的乘积。

这里的“有向长度”是指，如果 \(\mathbf{a}\) 在 \(b\) 上的投影向量与 \(\mathbf{b}\) 方向相同，则长度记为正，否则记为负。

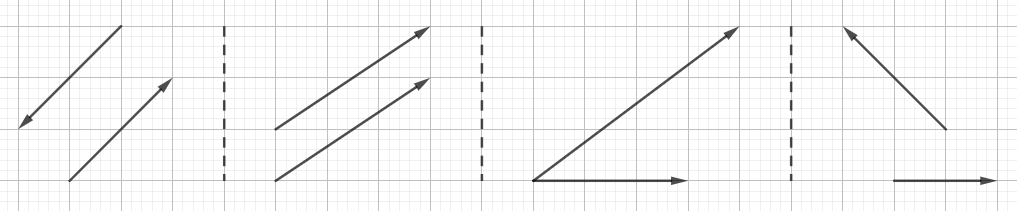
示例：计算图 6 所示四组向量的内积。

计算向量内积

向量内积的运算定律

向量内积满足交换律，即： \[\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a}\]

向量内积和加法满足分配律，即： \[(\mathbf{a}+\mathbf{b})\cdot\mathbf{c}=\mathbf{a}\cdot\mathbf{c}+\mathbf{b}\cdot\mathbf{c}\]

向量的数乘和内积满足如下定律：\[(\lambda\mathbf{a})\cdot\mathbf{b}=\lambda(\mathbf{a}\cdot\mathbf{b})\]

注：因为最后一条定律，你以写 \(\lambda\mathbf{a}\cdot\mathbf{b}\) 而无需指明运算次序。

在直角坐标系中，向量内积的计算方法很简单。

直角坐标系表示的内积计算

对于向量 \(\mathbf{a}=\begin{bmatrix} x_a\\y_a \end{bmatrix}, \mathbf{b}=\begin{bmatrix} x_b\\y_b \end{bmatrix}\) ，有：\(\mathbf{a}\cdot\mathbf{b}=x_ax_b+y_ay_b\)

证明将 \(\mathbf{a},\mathbf{b}\) 分解为 \(x\) 轴的投影与 \(y\) 轴的投影之和 \[\mathbf{a}=\mathbf{x_a}+\mathbf{y_a},\quad\mathbf{b}=\mathbf{x_b}+\mathbf{y_b}\] 有： \(\mathbf{a}\cdot\mathbf{b}=\mathbf{x_a}\mathbf{x_b}+\mathbf{y_a}\mathbf{y_b}+\mathbf{x_a}\mathbf{y_b}+\mathbf{y_a}\mathbf{x_b}\)

\(\because\) \(\mathbf{x_a}\perp \mathbf{y_b}\) 且 \(\mathbf{y_a}\perp \mathbf{x_b}\)

\(\therefore\) \(\mathbf{a}\cdot\mathbf{b}=\mathbf{x_a}\mathbf{x_b}+\mathbf{x_a}\mathbf{x_b}\)

\(\therefore\) \(\mathbf{a}\cdot\mathbf{b}=x_ax_b+x_ax_b\)

☐

示例：用直角坐标系计算图 7 所示四组向量的内积，并与之前使用投影进行计算的结果对比。

计算向量内积

向量的平面几何应用

在平面几何的计算中利用向量，尤其是在涉及平行、线段中点、垂直证明等问题上，往往会有非常好的效果。不仅如此，向量的表示往往能更体现几何图形的本质。

示例：说明三角形中位线平行于底边，且长度为底边的一半。

解：

利用向量的线性运算

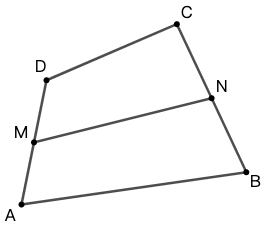
示例：（四边形的中位线的向量形式）任意四边形 \(ABCD\) 中（这四点无需在同一平面上），\(M\) 和 \(N\) 分别是 \(AD\) 和 \(BC\) 的中点，则 \(2\overrightarrow{MN}=\overrightarrow{AB}+\overrightarrow{CD}\) 。

四边形中位线的向量形式

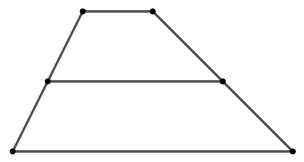
示例：（梯形的中位线定理-I）求证，梯形的中位线等于两底边长度之和的一半。

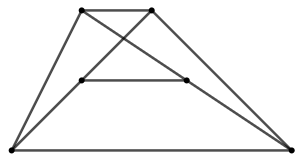
示例：（梯形的中位线定理-II）求证，梯形两对角线的中点两线平行于底边且等于两底边长度之差的一半。

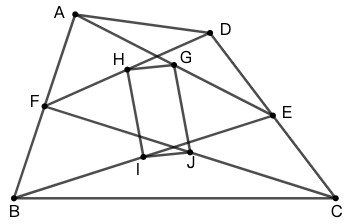
示例：如图 11 ，在四边形 \(ABCD\) 中，点 \(E\) 和 \(F\) 分别是 \(CD\) 和 \(AB\) 的中点，\(G,H,I,J\) 分别是 \(AE,DF,BE,CF\) 的中点。求证：四边形 \(GHIJ\) 为平行四边形。

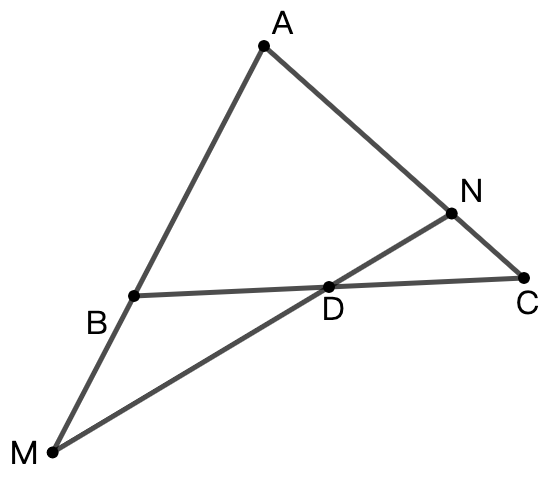
示例：如图 12 所示，点 \(O\) 是 \(BC\) 的中点，过点 \(O\) 的直线分别交直线 \(AB\) 和 \(AC\) 于不同的两点 \(M\) 和 \(N\) ，若 \(\overrightarrow{AB}=m\overrightarrow{AM},\overrightarrow{AC}=n\overrightarrow{AN}\) ，则 \(m+n\) 的值为 \(\_\_\_\_\_\_\) 。（2007年江西省高考试题）

向量的解析几何应用

在中学数学学习的体系中，向量是较高层次的抽象手段。为什么我们要学习高层次抽象的数学呢？同学们可以回想一下，当我们学习了一元一次方程之后，再看“鸡兔同笼”、“盈亏问题”、“百僧百馍”等应用题，就有豁然开朗的感觉。通过向量的抽象，我们可以将直角坐标系、三角函数和平面几何等主题联系起来。当你通过更高层次的视角回顾直角坐标系、三角函数和平面几何等主题时，你也会有类似的感觉。

直线方程的一般式

直线方程的一般形式为： \(Ax+By+C=0\) 。为了在很多情况下方便讨论，我们将常数项移到等号右侧，为了以示区分，使用小写字母表示系数和常数项，即：\[ax+by=c\]

令 \(\mathbf{n}=\begin{bmatrix} a\\b \end{bmatrix}\) 代表系数向量， \(\mathbf{p}=\begin{bmatrix} x\\y \end{bmatrix}\) 代表原点到平面上一点 \(P\) 的向量。那么直线方程可以写成： \[\mathbf{n}\cdot\mathbf{p}=c\]

根据向量内积的定义 \(\mathbf{n}\cdot\mathbf{p}\) 的几何意义是 \(\mathbf{p}\) 在 \(\mathbf{n}\) 上的有向投影长度与 \(\mathbf{n}\) 的长度的乘积。根据直线方程，所有满足条件的 \(p\) 向量在 \(\mathbf{n}=\begin{bmatrix} a\\b \end{bmatrix}\) 上的投影是等长的。因此这些点的集合应该是与 \(\mathbf{n}\) 垂直的直线。

示例：如图 13 所示，直线的方程是 \(3x+4y=12\) ，系数向量 \(\mathbf{n}=\begin{bmatrix} 3\\4 \end{bmatrix}\) 。可以看出直线 \(3x+4y=12\) 与 \(\mathbf{n}\) 垂直。

直线方程的向量视角

直线的法向量

与给定直线垂直的向量称为该直线的法向量 。特别地，对于直线 \(ax+by=c\) 来说， \(\mathbf{n}=\begin{bmatrix} a\\b \end{bmatrix}\) 是其法向量之一。

长度等于 \(1\) 的法向量称为单位法向量。特别地，对于直线 \(ax+by=c\) 来说， \(\dfrac{\mathbf{n}}{|\mathbf{n}|}\) 是其单位法向量之一。

请注意：法向量和单位法向量都是不唯一的。在平面上，直线有无数个法向量，有两个单位法向量。

做给定直线的平行线

示例：（过直线外一点做直线的平行线）如图 14 所示，给定直线 \(3x+4y=12\) 和直线外一点 \(G(-1,2)\) 。过 \(G\) 做给定直线的平行线，求平行线的直线方程。

过直线外一点做直线的平行线

解：原直线的系数向量为 \(\mathbf{n}=\begin{bmatrix} 3\\4 \end{bmatrix}\) ，该向量也是平行线的法向量。

令 \(\mathbf{g}=\begin{bmatrix} x\\y \end{bmatrix}\) ，于是平行线方程为： \(\mathbf{n}\cdot\mathbf{g}=\mathbf{n}\cdot\overrightarrow{OG}\)

整理得 \(3x+4y=5\)

如图 14 所示。

☐

平行线方程

直线 \(Ax+By+C=0\) 过 \((x_0,y_0)\) 的平行线方程为 \[Ax+By=Ax_0+By_0\]

点到直线的距离

示例：（点到直线的距离）如图 14 所示，给定直线 \(3x+4y=12\) 和直线外一点 \(G(-1,2)\) 。求直线到原点的距离，以及点 \(G\) 到直线的距离。

点到直线的距离

解：直线到原点的距离等于线段 \(OP_0\) 的长度。根据直线方程有： \[\overrightarrow{OP_0}\cdot\overrightarrow{ON}=12\]

由于 \(\overrightarrow{OP_0}\) 与 \(\overrightarrow{ON}\) 共线，所以 \[\overrightarrow{OP_0}\cdot\overrightarrow{ON}=12=|OP_0||ON|\] \[|OP_0|=\dfrac{12}{|ON|}=\dfrac{12}{\sqrt{3^2+4^2}}=2.4\]

即为直线到原点的距离。

点 \(G\) 到直线的距离等于线段 \(G_0P\) 的长度： \[|G_0P_0|=|OP_0|-|OG_0|=|OP_0|-\dfrac{\overrightarrow{OG}\cdot\overrightarrow{ON}}{|ON|}=2.4-1=1.4\]

综上所述，直线到原点距离为 \(2.4\) ，点 \(G\) 到直线距离为 \(1.4\) 。

☐

点到直线的距离公式

点 \((x_0,y_0)\) 到直线 \(Ax+By+C=0\) 的距离为 \[\dfrac{\left|Ax_0+By_0+C\right|}{\sqrt{A^2+B^2}}\]

做直线的垂线

示例：将平面向量 \(\mathbf{a}=\begin{bmatrix} 3\\4 \end{bmatrix}\) 顺时针旋转 \(90^\circ\) 。

解：令 \(x\) 和 \(y\) 方向的单位向量分别为 \(\mathbf{e_x}=\begin{bmatrix} 1\\0 \end{bmatrix}\) 和 \(\mathbf{e_y}=\begin{bmatrix} 0\\1 \end{bmatrix}\)

则 \(\mathbf{a}\) 可以表示为此二者的线性组合 \[\mathbf{a} =3\mathbf{e_x}+4\mathbf{e_y}\]

将 \(\mathbf{e_x},\mathbf{e_y}\) 顺时针旋转 \(90^\circ\) 得到 \[\mathbf{e'_x}=\begin{bmatrix} 0\\1 \end{bmatrix},\mathbf{e'_y}=\begin{bmatrix} -1\\0 \end{bmatrix}\]

其对应的线性组合即为 \(\mathbf{a}\) 顺时针旋转 \(90^\circ\) 的向量：

得到： \(\mathbf{a'}=3\mathbf{e'_x}+4\mathbf{e'_y}=\begin{bmatrix} -4\\3 \end{bmatrix}\)

☐

点绕原点顺时针旋转 \(90^\circ\)

坐标为 \((x,y)\) 的点绕原点顺时针旋转 \(90^\circ\) 后坐标为 \((-y,x)\) 。

向量 \(\begin{bmatrix} x\\y \end{bmatrix}\) 顺时针旋转 \(90\circ\) 后得到的新向量为 \(\begin{bmatrix} -y\\x \end{bmatrix}\)

示例：（过直线外一点做直线的垂线）过点 \(G(-1,2)\) 做直线 \(3x+4y=12\) 的垂线，求垂线方程。

解：直线 \(3x+4y=12\) 的法向量为 \(\begin{bmatrix} 3\\4 \end{bmatrix}\)

将其顺时针旋转 \(90^\circ\) 得到垂线的法向量为 \(\mathbf{n}=\begin{bmatrix} -4\\3 \end{bmatrix}\)

令 \(\mathbf{p}=\begin{bmatrix} x\\y \end{bmatrix}\) 于是垂线的方程为： \[\mathbf{n}\cdot\mathbf{p}=\mathbf{n}\cdot\overrightarrow{OG}\] \[-4x+3y=10\]

☐

垂线方程

直线 \(Ax+By+C=0\) 过 \((x_0,y_0)\) 的垂线方程为 \[-Bx+Ay=-Bx_0+Ay_0\]

旋转变换

示例：将平面向量 \(\mathbf{a}=\begin{bmatrix} 3\\4 \end{bmatrix}\) 逆时针旋转 \(60^\circ\) 。

旋转 \(60^\circ\)

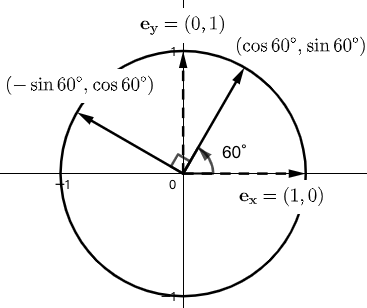
解：将 \(\mathbf{e_x},\mathbf{e_y}\) 逆时针旋转 \(60^\circ\) 得到 \[\mathbf{e'_x}=\begin{bmatrix} \cos60^\circ\\\sin60^\circ \end{bmatrix}=\begin{bmatrix} \dfrac{1}{2}\\\dfrac{\sqrt{3}}{2} \end{bmatrix},\quad\mathbf{e'_y}=\begin{bmatrix} -\sin60^\circ\\\cos60^\circ \end{bmatrix}=\begin{bmatrix} -\dfrac{\sqrt{3}}{2}\\\dfrac{1}{2} \end{bmatrix}\]

令 \(\mathbf{a}\) 逆时针旋转 \(60^\circ\) 后得到的向量为 \(\mathbf{a'}\)

得到：\(\mathbf{a'}=3\mathbf{e'_x}+4\mathbf{e'_y}=\begin{bmatrix} \dfrac{3-4\sqrt{3}}{2}\\ \dfrac{4+3\sqrt{3}}{2} \end{bmatrix}\)

☐

旋转变换

平面向量 \(\begin{bmatrix} x\\y \end{bmatrix}\) 逆时针旋转 \(\theta\) 角后变为： \(\begin{bmatrix} x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end{bmatrix}\)

示例：将 \(y=x^2\) 的图像逆时针旋转 \(60^\circ\) 。

解：新图像上的点逆时针旋转 \(-60^\circ\) 后落在 \(y=x^2\) 的图像上。

点 \((x,y)\) ，逆时针旋转 \(-60^\circ\) 后为 \((\dfrac{1}{2}x+\dfrac{\sqrt{3}}{2}y,-\dfrac{\sqrt{3}}{2}x+\dfrac{1}{2}y)\)

有： \(-\dfrac{\sqrt{3}}{2}x+\dfrac{1}{2}y=\left(\dfrac{1}{2}x+\dfrac{\sqrt{3}}{2}y\right)^2\)

整理得： \(\dfrac{1}{4}x^2+\dfrac{3}{4}y^2+\dfrac{\sqrt{3}}{2}xy+\dfrac{\sqrt{3}}{2}x-\dfrac{1}{2}y=0\)

☐

函数旋转 \(60^\circ\)

利用向量的内积运算

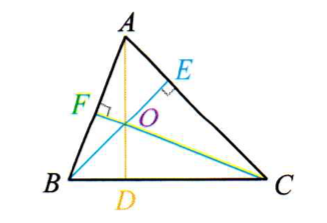
示例：（三角形的三条高交于一点）如图 18 所示，已知 \(\triangle{ABC}\) 中，\(BE\)、\(CF\) 交于点 \(O\) 且分别为 \(AC\)、\(AB\) 边上的高，\(AO\) 的延长线与 \(BC\) 交于点 \(D\) 。求证 \(AD\perp BC\) 。

计算向量内积

证明

\(\because\) \(BE\perp AC\)

\(\therefore\) \(\overrightarrow{OB}\cdot\overrightarrow{AC}=\overrightarrow{OB}\cdot(\overrightarrow{OC}-\overrightarrow{OA})=0\)\(\quad......\)

\(\therefore\) \(\overrightarrow{OB}\cdot\overrightarrow{OC}=\overrightarrow{OB}\cdot\overrightarrow{OA}\)

又\(\because\) \(CF\perp AB\)

\(\therefore\) \(\overrightarrow{OC}\cdot\overrightarrow{AB}=\overrightarrow{OC}\cdot(\overrightarrow{OB}-\overrightarrow{OA})=0\)\(\quad......\)

\(\therefore\) \(\overrightarrow{OC}\cdot\overrightarrow{OB}=\overrightarrow{OC}\cdot\overrightarrow{OA}\)

\(-\) 得到：

\(\overrightarrow{OB}\cdot\overrightarrow{OA}-\overrightarrow{OC}\cdot\overrightarrow{OA}=0\)

即 \((\overrightarrow{OB}-\overrightarrow{OC})\cdot\overrightarrow{OA}=\overrightarrow{CB}\cdot\overrightarrow{OA}=0\)

\(\therefore\) \(OB\perp OA\) ，即 \(AD\perp BC\) 。

☐

示例：如图 19 所示，\(D\) 是 \(\mathrm{Rt}\triangle{ABC}\) 斜边 \(AB\) 上的中点， \(E\) 和 \(F\) 分别在边 \(BC\) 和 \(AC\) 上，且 \(ED\perp FD\) ，求证： \(EF^2=AF^2+BE^2\) 。

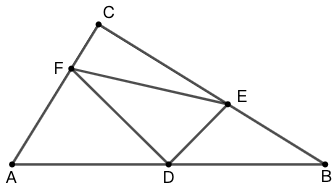
示例：如图 20 ，\(AB\) 是圆 \(O\) 的直径，过 \(A\) 和 \(B\) 引两条弦 \(AD\) 、\(BE\) 交于点 \(C\) 。求证： \(AB^2=AD\cdot AC+BE\cdot BC\) 。

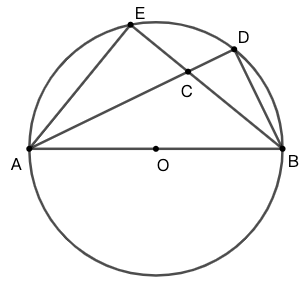
示例：求证直径所对的圆周角是直角。

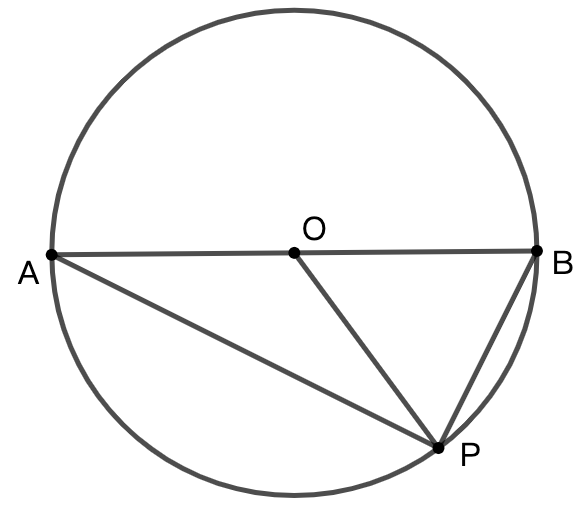
示例：

综合习题

练习：向量 \(\mathbf{a}=\begin{bmatrix} 3\\2 \end{bmatrix}\) ，以及正交单位向量 \(\mathbf{e_x}=\begin{bmatrix} 1\\0 \end{bmatrix},\ \mathbf{e_y}=\begin{bmatrix} 0\\1 \end{bmatrix}\)

将向量 \(\mathbf{a}\) 写成 \(\mathbf{e_x},\ \mathbf{e_y}\) 的线性组合 \(\mathbf{a}=\_\_\_\_\ \mathbf{e_x}+\_\_\_\_\ \mathbf{e_y}\)

练习：向量 \(\mathbf{a}=\begin{bmatrix} 3\\2 \end{bmatrix}\) ，以及向量 \(\mathbf{p_1}=\begin{bmatrix} 1\\1 \end{bmatrix},\ \mathbf{p_2}=\begin{bmatrix} 0\\1 \end{bmatrix}\)

将向量 \(\mathbf{a}\) 写成 \(\mathbf{p_1},\ \mathbf{p_2}\) 的线性组合 \(\mathbf{a}=\_\_\_\_\ \mathbf{p_1}+\_\_\_\_\ \mathbf{p_2}\)

练习：向量 \(\mathbf{a}=\begin{bmatrix} 3\\5 \end{bmatrix}\) ，以及向量 \(\mathbf{p_1}=\begin{bmatrix} 2\\1 \end{bmatrix},\ \mathbf{p_2}=\begin{bmatrix} 1\\2 \end{bmatrix}\)

将向量 \(\mathbf{a}\) 写成 \(\mathbf{p_1},\ \mathbf{p_2}\) 的线性组合 \(\mathbf{a}=\_\_\_\_\ \mathbf{p_1}+\_\_\_\_\ \mathbf{p_2}\)

练习：向量 \(\mathbf{a}=\begin{bmatrix} 3\\5 \end{bmatrix}\) ，以及向量 \(\mathbf{p_1}=\begin{bmatrix} 2\\2 \end{bmatrix},\ \mathbf{p_2}=\begin{bmatrix} 5\\1 \end{bmatrix}\)

将向量 \(\mathbf{a}\) 写成 \(\mathbf{p_1},\ \mathbf{p_2}\) 的线性组合 \(\mathbf{a}=\_\_\_\_\ \mathbf{p_1}+\_\_\_\_\ \mathbf{p_2}\)

练习： \(\bigstar\)上题中的线性方程组可以写成矩阵乘法（新运算）： \[\begin{bmatrix} 2 & 5\\2 & 1 \end{bmatrix}\begin{bmatrix} \lambda_1\\\lambda_2 \end{bmatrix}=\begin{bmatrix} 3\\5 \end{bmatrix}\]

求出线性组合系数后填入有： \[\begin{bmatrix} 2 & 5\\2 & 1 \end{bmatrix}\begin{bmatrix} 2.75\\-0.5 \end{bmatrix}=\begin{bmatrix} 3\\5 \end{bmatrix}\]

根据定义的新运算，求以下表达式的值： \[\begin{bmatrix} 1 & 2\\3 & 4 \end{bmatrix}\begin{bmatrix} 5\\6 \end{bmatrix}=?\]

练习：在图 22 中，写出平行线分线段成比例的向量表示

如果 \(\overrightarrow{AB}=\lambda\overrightarrow{AC},\ \overrightarrow{AD}=\lambda\overrightarrow{AE}\)，说明 \(BC\parallel DE\) 。
逆命题：如果 \(\overrightarrow{BC}=\lambda\overrightarrow{DE}\) ，说明 \(AB:AD=AC:AE\) 。

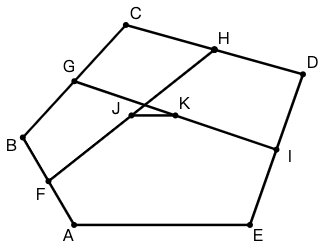
练习：如图 23 所示，五边形 \(ABCDE\) 中，点 \(F,G,H,I\) 分别是 \(AB,BC,CD,DE\) 的中点，点 \(J,K\) 分别是 \(FH\) 和 \(GI\) 的中点。求证： \(JK\parallel AE\) 且 \(JK=\dfrac{1}{4}AE\) 。

练习：已知向量 \(\mathbf{a}=\begin{bmatrix} 2\\2 \end{bmatrix}, \ \mathbf{b}=\begin{bmatrix} 0\\2 \end{bmatrix}\)

将向量的起点置于原点，在直角坐标系中画出这两个向量。
画出向量 \(\mathbf{a}\) 在 \(\mathbf{b}\) 上的投影，并用几何手段计算其长度。
画出向量 \(\mathbf{b}\) 在 \(\mathbf{a}\) 上的投影，并用几何手段计算其长度。
计算 \(\mathbf{a}\cdot\mathbf{b}\)

练习：已知向量 \(\mathbf{a}=\begin{bmatrix} 2\\2 \end{bmatrix}, \ \mathbf{b}=\begin{bmatrix} -2\\0 \end{bmatrix}\)

将向量的起点置于原点，在直角坐标系中画出这两个向量。
画出向量 \(\mathbf{a}\) 在 \(\mathbf{b}\) 上的投影，并用几何手段计算其长度。
画出向量 \(\mathbf{b}\) 在 \(\mathbf{a}\) 上的投影，并用几何手段计算其长度。
计算 \(\mathbf{a}\cdot\mathbf{b}\)

练习：已知向量 \(\mathbf{a}=\begin{bmatrix} -2\\-3 \end{bmatrix}, \ \mathbf{b}=\begin{bmatrix} -1\\2 \end{bmatrix}\)

使用内积的定义，求这两个向量夹角的余弦值。
使用余弦定理，求向量夹角的余弦值。
使用计算器，利用反三角函数计算向量夹角。
在直角坐标系中画出这两个向量，用量角器测量夹角。

练习：已知向量 \(\mathbf{a}=\begin{bmatrix} 2\\1 \end{bmatrix}, \ \mathbf{b}=\begin{bmatrix} 3\\-1 \end{bmatrix}\)

使用内积的定义，求这两个向量夹角的余弦值。
使用余弦定理，求向量夹角的余弦值。
使用计算器，利用反三角函数计算向量夹角。
在直角坐标系中画出这两个向量，用量角器测量夹角。

练习：在平面直角坐标系中，给定直线 \(l:\ 2x+y=4\)，以及直线外一点 \(G(-1,2)\)

在坐标系中画出该直线，以及直线的系数法向量。
写出与系数法向量同方向的单位向量。
写出直线方程的向量内积表示。

计算过点 \(G\) 且与 \(l\) 平行的直线方程。
计算过点 \(G\) 且与 \(l\) 垂直的直线方程。
计算点 \(G\) 到直线 \(l\) 的距离。

练习：在平面直角坐标系中，有直线 \(l_1:2x+y=4\) 与 \(l_2:2x+y=-2\) ，计算 \(l_1,\ l_2\) 的距离。(提示：计算直线上的点在法向量上的投影位置)

练习：推导直线距离公式。即在平面直角坐标系中，有直线 \(l_1:Ax+By+C_1=0\) 与 \(l_2:Ax+By+C_2=0\) ，求 \(l_1,\ l_2\) 的距离。

练习：计算直线 \(3x+4y=12\) 和 \(2x+y=5\) 夹角的正弦值。

练习：计算和直线 \(3x+4y=12\) 夹角为 \(45^\circ\) 的直线方程。（注意：有两个方向，各有无穷多条）

练习： \(\bigstar\)证明两直线的夹角为 \(45^\circ\) 时，斜率（如果存在）关系为 \(\left|\dfrac{k_1-k_2}{1+k_1k_2}\right|=1\)

练习：在平面直角坐标系中，到原点距离为 \(1\) 的点组成了单位圆。易知单位圆的方程为: \(x^2+y^2=1\)

将 \(y\) 替换为 \(y-1\) ，得到 \(x^2+(y-1)^2=1\) ，图像如何变化？
将 \(x\) 替换为 \(2x\) 得到 \(4x^2+y^2=1\) ，图像如何变化，为什么？
计算 \(4x^2+y^2=1\) 绕原点逆时针旋转 \(120^\circ\) 的图像方程。
在图形计算器或数学软件中绘图，验证你的答案。

练习：计算 \(y=\dfrac{1}{x}\) 顺时针旋转 \(45^\circ\) 之后的图像方程并绘制之。