三角函数-III：几何学应用

在 2002 年的全国高考北京卷中也致敬了这一经典结论，命题人以该定理作为背景编制了一道别出心裁的题目。

示例： 已知 \(O(0,0),\ B(1,0),\ C(b,c)\) 是 \(\triangle{OBC}\) 的三个定点。

1. 写出 \(\triangle{OBC}\) 的重心 \(G\) ，外心 \(F\) ，垂心 \(H\) 的坐标，并证明 \(G,F,H\) 三点共线；
2. 略

解析一 重心的坐标是点 \(G\left(\dfrac{1+b}{3},\dfrac{c}{3}\right)\)

外心的计算需要做两条中垂线计算，如图 1 所示，算得交点坐标：\(F\left(\dfrac{1}{2},\dfrac{b^2+c^2-b}{2c}\right)\)

外心的计算需要做两条高线计算，如图 2 所示，算得交点坐标：\(F\left(b,\dfrac{b-b^2}{c}\right)\)

☐

解析二 上述证明方法通过巧妙地设置坐标系的方法简化了计算。下面给出一种直接利用三角函数和相似三角形的证明思路。证明 \(\triangle{GFD}\sim\triangle{GHC}\) 即可，由于 \(HC\parallel FD\) 且 \(GC:GD=2:1\) ，只需再证明 \(HC:FD=2:1\) 即可。

欧拉线证明思路

☐

示例： 证明上述三角形内心坐标公式。

证明 通过三角形角平分线定理和梅涅劳斯定理即可证明：

示例： \(AB\) 为圆的直径，\(E\)、\(F\) 在 \(AB\) 上，\(AE=EF=FB=1\) ，圆上有一点 \(C\) ，求 \(CE+CF\) 的最大值。

ypma0207_eg01

解法一 （向量法）\(\overrightarrow{CE}=\overrightarrow{CO}+\overrightarrow{OE}\) ， \(\overrightarrow{CF}=\overrightarrow{CO}+\overrightarrow{OF}\)

\(|CE|^2+|CF|^2=\overrightarrow{CE}^2+\overrightarrow{CF}^2=(\overrightarrow{CO}+\overrightarrow{OE})^2+(\overrightarrow{CO}+\overrightarrow{OF})^2\)

注意到 \(\overrightarrow{OE}=-\overrightarrow{OF}\) ，有：

\(|CE|^2+|CF|^2=2|CO|^2+|OE|^2+|OF|^2=2.5\)

☐

解法二 （余弦定理）

\(CE^2=OC^2+OE^2-2\cdot OE\cdot OC\cos\angle{COE}\)

\(CF^2=OC^2+OF^2-2\cdot OF\cdot OC\cos\angle{COF}\)

注意到 \(\cos\angle{COE}=\cos\angle{COF}\) ，将上述两式相加得到：

\(CE^2+CF^2=2\cdot OC^2+OE^2+OF^2=2.5\)

☐

解法三 （坐标法）建立平面直角坐标系 \(A(-1.5,0),\ E(-0.5,0),\ F(0.5,0),\ B(1.5,0)\)

\(CE+CF=\sqrt{(x+0.5)^2+y^2}+\sqrt{(x-0.5)^2+y^2}\)

\(=\sqrt{1.25+x}+\sqrt{1.25-x}\)

☐

以上诸解法，其实是重新证明了“中线定理”：

请尝试证明之：

示例： 如图 5 所示，弦 \(CD\) 垂直于圆 \(O\) 的直径 \(AB\) 于 \(L\) ，弦 \(AE\) 平分半径 \(OC\) 于 \(H\) ，\(DE\) 交 \(BC\) 于 \(M\) . 求证：\(M\) 为 \(BC\) 中点。

ypma0207_eg10

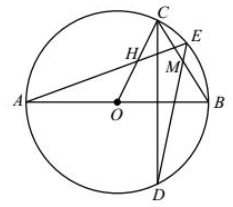
证明一 \(\angle{BAE}=\angle{BDE},\ \angle{CBD}=\angle{AOC}\)

\(\therefore\ \triangle{AOH}\sim\triangle{DBM}\) 从而 \(\dfrac{BM}{DB}=\dfrac{OH}{AO}=\dfrac{1}{2}\)

证明二 只需证明 M 为中点时，\(\angle{AED}\) 恰为 \(\wideparen{AD}\) 所对的圆周角即可。否则 \(M\) 不为中点时，\(\angle{AED}\) 会变化，无法满足 \(E\) 在圆周上的条件。

设 \(\angle{BOC}=\alpha\) ，注意到 \(\wideparen{AD}+\wideparen{BC}\) 是半圆周。

则可以列出诸点坐标如图 6 所示。

进一步求得： \(k_{AE}=\dfrac{\sin\alpha}{\cos\alpha+2}\) ， \(k_{DE}=\dfrac{3\sin\alpha}{1-\cos\alpha}\)

因为 \(\angle{AED}=\angle{BNE}-\angle{BAE}\) ，利用两角差的正切公式：

\(\tan\angle{AED}=\dfrac{k_{DE}-k_{AE}}{1+k_{AE}k_{AD}}=\dfrac{\dfrac{3\sin\alpha}{1-\cos\alpha}-\dfrac{\sin\alpha}{\cos\alpha+2}}{1+\dfrac{3\sin\alpha}{1-\cos\alpha}\cdot\dfrac{\sin\alpha}{\cos\alpha+2}}\)

分子分母同乘 \((1-\cos\alpha)\cdot(\cos\alpha+2)\) ，再展开合并同类项：

\(\tan\angle{AED}=\dfrac{4\sin\alpha\cos\alpha+5\sin\alpha}{-\cos^2\alpha-\cos\alpha+2+3\sin^2\alpha}=\dfrac{\sin\alpha(4\cos\alpha+5)}{-4\cos^2\alpha-\cos\alpha+5}\)

注意到分母等于 \((1-\cos\alpha)\cdot(4\cos\alpha+5)\) ，因此可以消去得到：

\(\tan\angle{AED}=\dfrac{\sin\alpha}{1-\cos\alpha}\)

利用万能公式：

\(\tan\angle{AED}=\dfrac{\dfrac{2\tan\dfrac{\alpha}{2}}{1+\tan^2\dfrac{\alpha}{2}}}{1-\dfrac{1-\tan^2\dfrac{\alpha}{2}}{1+\tan^2\dfrac{\alpha}{2}}}=\dfrac{1}{\tan\dfrac{\alpha}{2}}=\cot\dfrac{\alpha}{2}\)

☐

示例： 如图 7 所示，在 \(\triangle{ABC}\) 中 ，\(AB=AC=5\) ， \(BC=2\) ， 以 \(AB\) 为直径的圆 \(O\) 分别交 \(AC\) 、 \(BD\) 于 \(D\) 、 \(E\) ，求 \(\triangle{CDE}\) 的面积。

ypma0207_eg11

解： 连接 \(AE\) 、 \(BD\) ，有 \(AE\perp BC\) 、\(BD\perp AC\)

因为 \(\triangle{ABC}\) 是等腰三角形，所以 \(AE\) 是中线 \(BE=EC=1\) 。

\(\sin\angle{B}=\sin\angle{C}=\dfrac{\sqrt{24}}{5}\)

\(\cos\angle{BAC}=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=0.92\)

\(AD=AE\cdot\cos\angle{BAC}=4.6\) ， \(CD=AC-AD=0.4\)

☐

示例： 如图 8 所示，AB是圆 \(O\) 直径，弦 \(CD\perp AB\) 于 \(G\)，\(E\) 在 \(\wideparen{AC}\) 上，直线 \(AE\) 与 \(CD\) 交于 \(F\)， \(\dfrac{CF}{AF}=\dfrac{CG}{AG}\)。

求证: \(AB\cdot CD=2AE\cdot CF\) 。

ypma020_eg12

证明 设 \(\angle{BAC}=\theta\) ，由角平分线定理可知 \(AC\) 为 \(\angle{BAF}\) 的角平分线，故 \(\angle{BAF}=2\theta\)。于是可以将所有的线段长度表示为 \(AB\) 和 \(\theta,2\theta\) 的三角函数的乘积：

\(AC=AB\cos\theta,\ \ AE=AB\cos2\theta\)

\(CG=AC\sin\theta=AB\cos\theta\sin\theta\)

\(CD=2CG=2AB\cos\theta\sin\theta\)

\(AG=AC\cos\theta=AB\cos^2\theta\)

\(AF=\dfrac{AG}{\cos2\theta}=\dfrac{cos^2\theta}{\cos2\theta}\)

\(CF=\dfrac{AF\cdot CG}{AG}=\dfrac{\cos\theta\sin\theta}{\cos2\theta}\)

\(AB\cdot CD=2AB^2\cos\theta\sin\theta=2AE\cdot CF\)

☐

示例： 如图 9 所示，在 \(\triangle{ABC}\) 中 ，\(AB=8,\ AC=6\) ， 以 \(AC\) 为直径的圆交 \(\angle{A}\) 的外角平分线于 \(E\) ， \(D\) 为 \(BC\) 中点，求 \(DE\) 的长。

ypma0207_eg13

示例： 如图 10 所示，在锐角 \(\triangle{ABC}\) 中 ，\(BE\perp AC\) 于 \(E\) ， \(CD\perp AB\) 于 \(D\) ， \(BC=25\) ， \(CE=7\) ， \(BD=15\) ，若 \(BE\) 交 \(CD\) 于 \(H\) ，以 \(DE\) 为直径做圆与 \(AC\) 交于另一点 \(F\) ，求 \(AF\) 。

ypma0207_eg14

解： 根据勾股定理 \(BE=24\) ，故 \(\cos\angle{CBE}=\dfrac{24}{25},\ \sin\angle{CBE}=\dfrac{7}{25}\)

又据勾股定理 \(CD=20\) ，故 \(\cos\angle{CBE}=\dfrac{3}{5},\ \sin\angle{CBD}=\dfrac{4}{5}\)

因为 \(\angle{ABE}=\angle{CBD}-\angle{CBD}\)

所以 \(\cos\angle{ABE}=\cos\angle{CBD}\cos\angle{CBE}+\sin\angle{CBD}\sin\angle{CBE}=\dfrac{4}{5}\)

因此 \(AB=30,\ AE=18\)

因为 \(\angle{DFE}=90^\circ\) ，所以 \(DF\parallel BE\)

☐

示例： 如图 11 所示，四边形 \(ABCD\) 内接于圆 \(O\) ， \(AB\) 是直径， \(AD=CD\) ，分别延长 \(BA\) 、 \(CD\) 交于点 \(E\) ，作 \(BF\perp EC\) ，并与 \(EC\) 的延长线交于点 \(F\) ， \(AE=AO\) ， \(BC=6\) ，求 \(CF\) 的长。

ypma0207_eg15

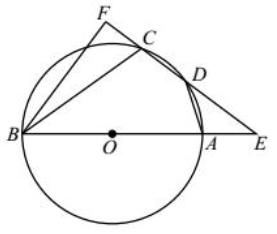
解 \(\because\ \wideparen{CD}=\wideparen{DA}\)\(\therefore\ \angle{AOD}=\angle{ABC}\)

\(\therefore\ OD\parallel BC,\ CD:DE=1:2,\ OD=4=r\)，

在 \(Rt\triangle{ABC}\) 中， \(\cos\angle{ABC}=\dfrac{3}{4},\ \sin\angle{ABC}=\dfrac{\sqrt{7}}{4}\)

解 \(\triangle{ABC}\) ，求得 \(EC=6\sqrt{2}\)， \(\cos\angle{E}=\dfrac{5}{4\sqrt{2}}\)

☐

注：小猿搜题能搜出来一个相似三角形解法，附到下页

示例： 如图 12 所示，在梯形 \(ABCD\) 中， \(AB\parallel CD\) ， \(\angle{ABC}=90^\circ\) ，以 \(AD\) 为直径的圆交 \(BC\) 于 \(E\) 。

求证： \(AB\cdot DE+BE\cdot AE=BC\cdot AE\)

ypma0207_eg16

证明 \(\angle{AED}=90^\circ\)

\(\therefore\ \triangle{CDE}\sim\triangle{BEA}\)

\(\therefore\ DE=\dfrac{CE\cdot AE}{AB}\)

☐

附： ypma0207_eg15 另解 小猿搜题搜出来相似三角形解法

ypma0207_eg15

示例： 如图 15 所示，过平行四边形 \(ABCD\) 的定点 \(A\) 作一圆分别交 \(AB\) 、 \(AC\) 、 \(AD\) 于 \(E\) 、 \(F\) 、 \(G\) 。

求证： \(AF\cdot AC=AE\cdot AB + AG\cdot AD\)

ypma0207_eg17

证明 观察图形的自由度，确定为 \(AC,AF,\alpha,\beta,\gamma\)

由正弦定理：

$= = $

\(\dfrac{AD}{\sin\beta}=\dfrac{AC}{\sin(180^\circ-(\alpha+\beta))} \quad\Leftrightarrow\quad \dfrac{AD}{\sin\beta}=\dfrac{AC}{\sin(\alpha+\beta)}\)

得到： \(AG=AF\cdot\dfrac{\sin(\alpha+\gamma)}{\sin\gamma},\ \ AD=AC\cdot\dfrac{\sin\beta}{\sin(\alpha+\beta)}\)

类似地：\(AE=AF\cdot\dfrac{\sin(\gamma-\beta)}{\sin\gamma},\ \ AB=AC\cdot\dfrac{\sin\alpha}{\sin(\alpha+\beta)}\)

\(AE\cdot AB+AC\cdot AD=AF\cdot AC\dfrac{\sin(\alpha+\gamma)\sin\beta+\sin(\gamma-\beta)\sin\alpha}{\sin\gamma\sin(\alpha+\beta)}\)

\(\qquad=AF\cdot AC\cdot\dfrac{\sin\alpha\cos\gamma\sin\beta+\cos\alpha\sin\gamma\sin\beta+\sin\gamma\cos\beta\sin\alpha-\cos\gamma\sin\beta\sin\alpha}{\sin\gamma\sin(\alpha+\beta)}\)

\(\qquad=AF\cdot AC\cdot\dfrac{\cos\alpha\sin\gamma\sin\beta+\sin\gamma\cos\beta\sin\alpha}{\sin\gamma\sin(\alpha+\beta)}\)

\(\qquad=AF\cdot AC\cdot\dfrac{\sin\gamma(\cos\alpha\sin\beta+\cos\beta\sin\alpha)}{\sin\gamma\sin(\alpha+\beta)}\)

\(\qquad=AF\cdot AC\cdot\dfrac{\sin\gamma\sin(\alpha+\beta)}{\sin\gamma\sin(\alpha+\beta)}\)

☐

示例： 如图 17 所示， \(AB\) 是圆 \(O\) 的直径，若 \(\angle{M}=20^\circ,\ \angle{CBD}=40^\circ\) ， 求 \(\angle{BDC}\) 。

ypma0207_eg18

证明 观察到如果 \(\angle{BDC}\) 的角度确定，图形的形状就确定了。所以解题思路是把两个条件挑一个（例如 \(\angle{M}=20^\circ\)）出来留着列方程，用另一个条件（如 \(\angle{CBD}=40^\circ\)）和 \(\angle{CDB}=x^\circ\) 计算所有的角度。

列出方程为 \(2x-50=20\) ，解得 \(x=30\) 。

☐

示例： 如图 19 所示，已知四边形 \(ABCD\) 外接圆 \(O\) 的半径为 \(2\) ，对角线 \(AC\) 与 \(BD\) 交点为 \(E\) ， \(AE=EC\) ， \(AB=\sqrt{2}AE\) ， \(BD=2\sqrt{3}\) ，求四边形 \(ABCD\) 的面积。

ypma0207_eg19

证明 图形就一个自由度，设 \(\angle{AEB}=\alpha\) 。根据 \(BD=2\sqrt{3}\) ，得到 \(OH=1\) ，再根据三角函数关系写出 \(OE=\dfrac{1}{\cos\alpha}\) ， \(HE=\tan\alpha\) 。在直角三角形 \(AEO\) 中运用勾股定理得到 \(AE=\sqrt{1-\dfrac{1}{\cos^2\alpha}}\) 。

使用余弦定理计算 \(AB\) 的长度，再利用 \(AB=\sqrt{2}AE\) 的条件：

\(AB^2=AE^2+BE^2-2\cdot AE\cdot BE\cdot\cos\alpha\)

\(2AE^2=AE^2+BE^2-2\cdot AE\cdot BE\cdot\cos\alpha\)

\(BE^2-AE^2=-2\cdot AE\cdot BE\cdot\cos\alpha\)

\((\sqrt{3}+\tan\alpha)^2-(4-\dfrac{1}{\cos^2\alpha})=2\sqrt{4-\dfrac{1}{\cos^2\alpha}}\cdot(\sqrt{3}+\tan\alpha)\cdot\cos\alpha\)

\(2\sqrt{3}\tan\alpha+2\tan^2\alpha=2\sqrt{4-\dfrac{1}{\cos^2\alpha}}\cdot(\sqrt{3}+\tan\alpha)\cdot\cos\alpha\)

\(\tan\alpha=\sqrt{4-\dfrac{1}{\cos^2\alpha}}\cdot\cos\alpha\)

\(\dfrac{\sin\alpha}{\cos^2\alpha}=\sqrt{4-\dfrac{1}{\cos^2\alpha}}\)

\(\dfrac{\sin^2\alpha}{\cos^4\alpha}=4-\dfrac{1}{\cos^2\alpha}\quad\Leftrightarrow\quad\dfrac{1-\cos^2\alpha}{\cos^4\alpha}=4-\dfrac{1}{\cos^2\alpha}\)

\(\cos^4\alpha=\dfrac{1}{4}\) ，\(\alpha\) 是锐角，\(\cos\alpha=\dfrac{\sqrt{2}}{2}=\sin\alpha\)

☐

示例： 四边形 \(ABCD\) 内接于圆 \(O\) ， \(AC\perp BD\) 。 \(OE\) 、\(OF\) \(OG\) \(OH\) 分别垂直于 \(AB\) \(BC\) \(CD\) \(DA\) 。

求证： \(AB+BC+CD+DA=2(OE+OF+OG+OH)\)

证明 不妨设圆的半径为 \(1\) ，把两条对角线置于平面直角坐标系中水平和垂直的位置，并且放在 \(y\) 轴的右边和 \(x\) 轴的上边，

ypma0207_ex04_ans

根据圆心角计算弦长：

\(AB=2\sin\dfrac{\alpha-\beta}{2},\qquad BC=2\sin\dfrac{\alpha+\beta}{2}\)

\(CD=2\sin\dfrac{180^\circ-(\alpha-\beta)}{2}=2\cos\dfrac{\alpha-\beta}{2}\)

\(DA=2\sin\dfrac{180^\circ-(\alpha+\beta)}{2}=2\cos\dfrac{\alpha+\beta}{2}\)

根据三角函数的定义可以得到一堆垂线的长度：

\(OE=\cos\dfrac{\alpha-\beta}{2},\quad OF=\cos\dfrac{\alpha+\beta}{2}\)

\(OG=\sin\dfrac{\alpha+\beta}{2},\quad OH=\sin\dfrac{\alpha-\beta}{2}\)

☐

☐

示例： 以线段 \(AB\) 为直径作半圆，圆心为 \(O\) ，\(C\) 是半圆上的点，且\(OC^2=AC\cdot BC\) ，求 \(\angle{CAB}\) 。

证明二 不妨设 \(OC=1\) ，设 \(\angle{BOC}=\alpha\)

ypma0207_ex05_ans

\(BC=2\sin\dfrac{\alpha}{2},\quad AC=2\sin(\dfrac{\pi-\alpha}{2})=2\cos\dfrac{\alpha}{2}\)

\(AC\cdot AB=4\cos\dfrac{\alpha}{2}\sin\dfrac{\alpha}{2}=2\sin\alpha=OC^2=1\)

\(\sin\alpha=\dfrac{1}{2}\) 得到 \(\alpha=30^\circ\ or\ 150^\circ\)

☐

证明二 依然不妨设 \(OC=1\) ，设 \(\angle{BOC}=\alpha\)

\(|OC|^2=|OA|^2|OB|^2=(\overrightarrow{OC}-\overrightarrow{OB})^2(\overrightarrow{OC}-\overrightarrow{OA})^2=1\qquad\Leftrightarrow\)

\((\overrightarrow{OC}^2+\overrightarrow{OB}^2-2\overrightarrow{OC}\cdot\overrightarrow{OB})(\overrightarrow{OC}^2+\overrightarrow{OA}^2-2\overrightarrow{OC}\cdot\overrightarrow{OA})=1\qquad\Leftrightarrow\)

\((2-2\overrightarrow{OC}\cdot\overrightarrow{OB})(2-2\overrightarrow{OC}\cdot\overrightarrow{OA})=1\qquad\Leftrightarrow\)

\(1-\overrightarrow{OC}\cdot\overrightarrow{OB}-\overrightarrow{OC}\cdot\overrightarrow{OA}+(\overrightarrow{OC}\cdot\overrightarrow{OB})(\overrightarrow{OC}\cdot\overrightarrow{OA})=\dfrac{1}{4}\)

由于 \(\overrightarrow{OB}=-\overrightarrow{OA}\) 得到：

\((\overrightarrow{OC}\cdot\overrightarrow{OB})(\overrightarrow{OC}\cdot\overrightarrow{OA})=-\dfrac{3}{4}\quad\Leftrightarrow\quad\cos\alpha\cos(\pi-\alpha)=-\dfrac{3}{4}\)

\(\cos^2\alpha=\dfrac{3}{4}\quad\Leftrightarrow\quad\cos\alpha=\pm\dfrac{\sqrt{3}}{2}\) 得到 \(\alpha=30^\circ\ or\ 150^\circ\)

☐

示例： 如图 23 所示，圆 \(O\) 的直径 \(AB\) 的长为 \(10\) ，弦 \(AC\) 长为 \(6\) ，\(\angle{ACB}\) 的平分线交圆 \(O\) 于 \(D\) ，求 \(CD\) 的长。

ypma0207_ex07

解： 根据勾股定理 \(BC=8\) 。

连接 \(OC\) 有 \(\angle{OCA}=\angle{OAC}\) ，\(\angle{ACD}=45^\circ\)

\(\angle{OCD}=\angle{OCA}-\angle{ACD}\)

\(\cos\angle{OCD}=\cos\angle{OCA}\cos\angle{ACD}+\sin\angle{OCA}\sin\angle{ACD}\)

\(\cos\angle{OCD}=\dfrac{3}{5}\cdot\dfrac{\sqrt{2}}{2}+\dfrac{4}{5}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{7\sqrt{2}}{10}\)

☐

示例： 如图 24 所示，\(P\) 是等边 \(\triangle{ABC}\) 外接圆的弧 \(\wideparen{BC}\) 上的任意一点，\(AP\) 交 \(BC\) 于 \(D\) ， 求证：\(PA^2=AC^2+PB\cdot PC\) 。

ypma0207_ex12

证明 不妨设圆的半径为 \(1\) ，则 \(AC=BA=BC=\sqrt{3}\) 。

令 \(\angle{BAP}=\alpha\) ，

则 \(AP=2\cos(30^\circ-\alpha),\ PC=2\cos(30^\circ+\alpha),\ PB=2\sin\alpha\)

\(PA^2-PB\cdot PC=4\cos^2(30^\circ-\alpha)-2\sin\alpha\cdot2\cos(30^\circ+\alpha)\)

\(\qquad=4\left(\dfrac{\sqrt{3}}{2}\cos\alpha+\dfrac{1}{2}\sin\alpha\right)^2-4\sin\alpha\left(\dfrac{\sqrt{3}}{2}\cos\alpha-\dfrac{1}{2}\sin\alpha\right)\)

\(\qquad=3\cos^2\alpha+\sin^2\alpha+2\sqrt{3}\sin\alpha\cos\alpha-2\sqrt{3}\sin\alpha\cos\alpha+2\sin^2\alpha\)

\(\qquad=3=AC^2\)

☐

示例： 如图 25 所示，圆 \(O\) 与直角\(\triangle{AOB}\) 的斜边交于 \(C\) 、 \(D\) 两点， \(C\) 、\(D\) 是线段 \(AB\) 的三等分点，若圆 \(O\) 的半径为 \(5\) ，求 \(AB\) 的长。

ypma0207_ex14

解： 做 \(OH\perp AB\) 于 \(H\)，

由于 \(CD\) 是三等分点，易证 \(OA=OB,\ OH=3CH=\dfrac{1}{2}AB\)

得到 \(\tan\angle{COH}=\dfrac{1}{3},\ \cos\angle{COH}=\dfrac{3}{\sqrt{10}}\)

☐

示例： 如图 26 所示，圆 \(O\) 与正方形 \(ABCD\) 四边的交点为 \(E\)、\(F\)、\(G\)、\(H\)、\(I\)、\(J\)、\(K\)、\(L\)。

求证：　\(AL + AE + CH + CI = BF + BG + DJ + DK\)

ypma0207_ex15

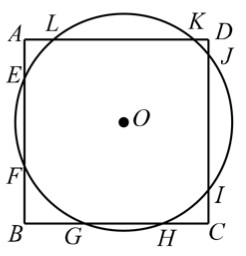
解： 如图建立平面直角坐标系，将正方形的中心置于坐标系原点，设圆 \(O\) 的圆心置于 \((x,y)\) 。

设正方形边长为 \(2a\) ，圆的半径为 \(r\) ，可以计算诸线段长度为：

\(AL=a+x-\sqrt{r^2-(a-y)^2},\quad AE=a-y-\sqrt{r^2-(a+x)^2}\)

\(BF=a+y-\sqrt{r^2-(a+x)^2},\quad BG=a+x-\sqrt{r^2-(a+y)^2}\)

\(CH=a-x-\sqrt{r^2-(a+y)^2},\quad CI=a+y-\sqrt{r^2-(a-x)^2}\)

\(DJ=a-y-\sqrt{r^2-(a-x)^2},\quad DK=a-x-\sqrt{r^2-(a-y)^2}\)

☐

示例： 已知正方形和三角形都外切于一个半径为 \(1\) 的圆。求证：在圆的外部正方形和三角形的面积大于 \(0.34\) 。

分析 本题只要证明圆外切三角形的面积最小时为正三角形即可。如图 28 所示，\(\triangle{DEF}\) 是圆 \(O\) 的外切三角形，切点为 \(A,B,C\) 。

ypma0207_ex16_ans

容易得到 \(S_{\triangle{ABC}}=\tan\alpha+\tan\beta+\tan\gamma\ ,\quad\alpha,\beta,\gamma\in(0,\dfrac{\pi}{2})\)

我们需要在 \(\alpha+\beta+\gamma=180^\circ\) 的约束条件下求最小值。

由于 \(\tan(x)\) 是 \((0,\dfrac{\pi}{2})\) 上的下凸函数，根据下图可以证明： \[\tan\alpha+\tan\beta+\tan\gamma\geq\tan\dfrac{\alpha+\beta}{2}+\tan\dfrac{\alpha+\beta}{2}+\tan\gamma\]

令 \(\theta=\dfrac{\alpha+\beta}{2}\) ，利用下图的三等分点可以证明：\[\tan\dfrac{\alpha+\beta}{2}+\tan\dfrac{\alpha+\beta}{2}+\tan\gamma\geq3\tan\dfrac{\alpha+\beta+\gamma}{3}\]

☐

示例： 如图， \(AB\) 为 \(\odot O\) 直径，且 \(AB=4\sqrt{2}\) 。点 \(C\) 为半圆上一动点（不与 \(A,B\) 重合）， \(D\) 为弧 \(CB\) 上一点，点 \(E\) 在 \(AD\) 上，且 \(CD=BD=DE\) ，求 \(CE\) 长度的最大值。