三角函数-II:任意角的三角函数
任意角的定义
为了进一步研究三角函数,需要对“角”这一概念进行扩展。
任意角的定义
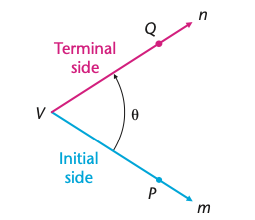
一条射线绕其端点旋转到另一条射线所形成的图形称为角,射线的端点称为角的定点,这两条射线分别称为角的始边(initial side)和终边(terminal side)。
习惯上规定,按照逆时针方向旋转而成的角称为正角(positive angle) ,如图 2(a)。按照顺时针方向旋转而成的角称为负角(negative angle),如图 (b)。
当射线没有旋转时,我们也把它看成一个角,称为零角。这样定义的角,由于是旋转生成的,所以也常称为转角。
当两个角的边旋转至重合位置时,我们称之为“终边相同的角”(to be coterminal) ,如图 2(c) 所示。
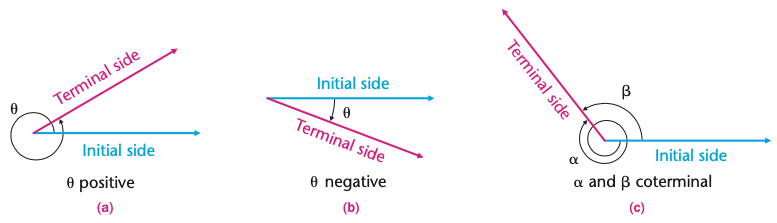
为了研究和讨论的方便,我们常常将角置于平面直角坐标系中的标准位置:顶点位于原点,始边位于 \(x\) 正半轴。
象限角
如果处于标准位置的角,其终边落在坐标轴上,则称为象限角。如果终边不在坐标轴上,则根据终边所在的具体象限,称为第几象限角。
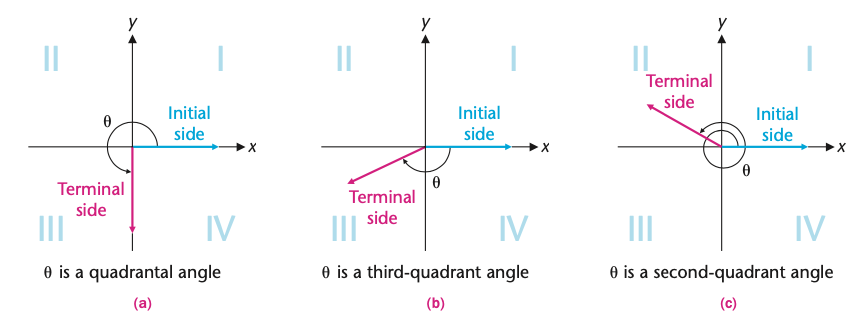
弧度制
为了描述一个角的大小,我们有两种方法:角度制和弧度制。角度制将圆周分为 \(360\) 度,将 \(1\) 度分为 \(60\) 分,将 \(1\) 分再细分为 \(60\) 秒。弧度制则是将圆周对应为 \(2\pi\) ,欲度量的角各取其分即可。从小学至初中,同学们已经熟悉了角度制。从本章开始,我们将引入弧度制。
在讲述弧度制之前,我们先通过一道例题复习一下角度制。
示例: 将“度-分-秒”(DMS) 格式为十进制度(DD)格式。
将 \(21^\circ47'12"\) 转换为 DD 格式
将 \(105.183^\circ\) 转换为 DMS 格式
过渡段
弧度制
弧度制将圆周规定为 \(2\pi\) 弧度(rad)(角度制则规定为 \(360^\circ\))。弧度是一个无量纲量,所以在运算过程中无需写出单位。
初学者应当首先熟悉各象限角的角度制和弧度制的互换:\(90^\circ\) 角对应 \(\dfrac{\pi}{2}\) 弧度 ,\(180^\circ\) 角对应 \(\pi\) 弧度 ,\(270^\circ\) 角对应 \(\dfrac{3\pi}{2}\) 弧度 ,\(360^\circ\) 角对应 \(2\pi\) 弧度。
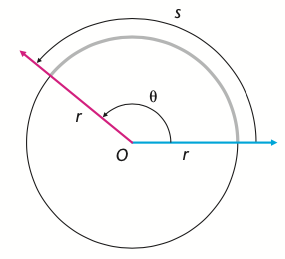
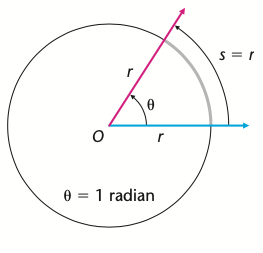
弧度制的一个优势是在计算圆弧的长度时,只需要使用半径乘以圆弧所对的圆心角即可。如图 4 所示,弧长 \(s\) ,其所对的圆心角 \(\theta\) 和半径 \(r\) 的关系如下:\[s=r\cdot\theta\]
在弧度制下,\(1\) 弧度的圆心角所对圆弧的长度恰为圆的半径 \(r\) ,如图 5 所示。
示例: 在半径为 \(4\mathrm{cm}\) 的圆上,长度为 \(10\mathrm{cm}\) 的一段圆弧,对应的圆心角是多少弧度?
解: \[\theta=\dfrac{s}{r}=\dfrac{20\mathrm{cm}}{4\mathrm{cm}}=2.5 \quad\mathrm{rad}\]☐
示例: 根据要求,在角度制和弧度制之间进行转换:
- [(1)] 将 \(75^\circ\) 转换为弧度制,分别给出用 \(\pi\) 表示的精确结果和保留三位有效数字的结果。
- [(2)] 将 \(5\) 弧度转换为角度制,分别给出用 \(\pi\) 表示的精确结果和保留四位有效数字的结果。
- [(3)] 将 \(41^\circ12'\) 转换为弧度制,保留小数点后两位数字。
三角函数的单位圆定义
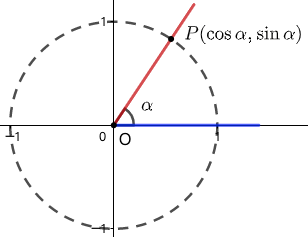
三角函数的单位圆定义
平面直角坐标系中,坐标满足 \(x^2+y^2=1\) 的点组成的集合称为单位圆。处于标准位置的角 \(\alpha\) 的终边与单位圆交点为 \(P\) ,如图 6 所示,则 \(P\) 点坐标为: \[(\cos\alpha,\sin\alpha)\] 也就是说,角 \(\alpha\) 的余弦和正弦分别等于点 \(P\) 的横坐标和纵坐标。当终边不在 \(y\) 轴上时,角 \(\alpha\) 的正切值定义为:\[\tan\alpha=\dfrac{\cos\alpha}{\sin\alpha}\] 即点 \(P\) 的纵坐标与横坐标的比值。
通过任意角的三角函数和弧度制的定义,我们在全实数轴上定义了“角度”这一概念。
两角和与差的三角函数
示例: 将单位向量 \(\mathbf{p}=\begin{bmatrix} 1\\0 \end{bmatrix}\) 逆时针旋转 \(\alpha\) 角后的向量为 \(\mathbf{p'}=\begin{bmatrix} \cos\alpha\\\sin\alpha \end{bmatrix}\) 。计算将 \(\mathbf{p'}\) 再逆时针旋转 \(\beta\) 角后的向量 \(\mathbf{p''}\) 。
解: \(\mathbf{p'}=\cos\alpha\cdot\mathbf{e_x}+\sin\alpha\cdot\mathbf{e_y}\) ,将 \(\mathbf{e_x}\) 轴和 \(\mathbf{e_y}\) 逆时针旋转 \(\beta\) 角后,用同样的线性组合系数产生 \(p''\) :
\(\mathbf{p''}=\cos\alpha\cdot\mathbf{e'_x}+\sin\alpha\cdot\mathbf{e'_y}=\cos\alpha\begin{bmatrix} \cos\beta\\\sin\beta \end{bmatrix}+\sin\alpha\begin{bmatrix} -\sin\beta\\\cos\beta \end{bmatrix}\)
\(\mathbf{p''}=\begin{bmatrix} \cos\beta & -\sin\beta\\\sin\beta & \cos\beta\end{bmatrix}\begin{bmatrix} \cos\alpha\\\sin\alpha \end{bmatrix}\)
☐
示例: 将单位向量 \(\mathbf{p}=\begin{bmatrix} 1\\0 \end{bmatrix}\) 逆时针旋转 \(\alpha\) 角后的向量为 \(\mathbf{e'_x}=\begin{bmatrix} \cos\alpha\\\sin\alpha \end{bmatrix}\) 。计算将 \(\mathbf{p'}\) 再顺时针旋转 \(\beta\) 角后的向量 \(\mathbf{p''}\) 。
综上所述,可以得到如下结论:
两角和的正弦和余弦
\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\)
思考与讨论
- 如何说明 \(\mathbf{e_y}\) 逆时针旋转 \(\beta\) 角之后的向量为 \(\begin{bmatrix} -\sin\beta\\\cos\beta \end{bmatrix}\) ?
请注意,你在这里不能使用诱导公式,也不能使用两角和三角函数的公式,因为我们还没有得到它们。
示例: 将 \(\tan(\alpha+\beta)\) 写成 \(\tan\alpha\) 和 \(\tan\beta\) 的函数。
解: \(\tan(\alpha+\beta)=\dfrac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\dfrac{\cos\alpha\sin\beta+\sin\alpha\cos\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\)
将分子分母同时除以 \(\cos\alpha\cos\beta\) 得到:
\(\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)☐
示例: 将 \(\tan(\alpha-\beta)\) 写成 \(\tan\alpha\) 和 \(\tan\beta\) 的函数。
进一步由 \(\tan\beta=\cot^{-1}\beta\),可以得到如下结论:
两角和的正切和余切
\(\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\) \(\cot(\alpha+\beta)=\dfrac{1-\tan\alpha\tan\beta}{\tan\alpha+\tan\beta}\)
\(\tan(\alpha-\beta)=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\) \(\cot(\alpha-\beta)=\dfrac{1+\tan\alpha\tan\beta}{\tan\alpha-\tan\beta}\)
在上述公式中,令 \(\alpha=\beta\) 即可得到常用的二倍角公式:
二倍角公式
\(\cos2\alpha=\cos^2\alpha-\sin^2\alpha\ =\ 2\cos^2\alpha-1\ =\ 1-2\sin^2\alpha\)
\(\sin2\alpha=2\sin\alpha\cos\alpha\)
\(\tan2\alpha=\dfrac{2\tan\alpha}{1-\tan^2\alpha}\) 这个公式连同下面两个合称“万能公式”
\(\cos2\alpha=\dfrac{1-\tan^2\dfrac{\alpha}{2}}{1+\tan^2\dfrac{\alpha}{2}}\ \ ,\ \ \sin2\alpha=\dfrac{2\tan\dfrac{\alpha}{2}}{1+\tan^2\dfrac{\alpha}{2}}\)
再利用 \(3\alpha=2\alpha+\alpha\) 三倍角公式:
三倍角公式
\(\cos3\alpha=-3\cos\alpha+4\cos^3\alpha\) \(\sin3\alpha=3\sin\alpha-4\sin^3\alpha\)
\(\tan3\alpha=\dfrac{3\tan\alpha-\tan^3\alpha}{1-3\tan^2\alpha}\) \(\cot3\alpha=\dfrac{-3\cot\alpha+\cot^3\alpha}{3\cot^2\alpha-1}\)
示例: 计算 \(\sin\dfrac{\pi}{12}\) 。
解: \(\sin\dfrac{\pi}{12}=\sin\left(\dfrac{\pi}{4}-\dfrac{\pi}{6}\right)\)
根据两角差的正弦公式:
\(\sin\left(\dfrac{\pi}{4}-\dfrac{\pi}{6}\right)=\sin\left(\dfrac{\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)-\cos\left(\dfrac{\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\)
因此,\(\sin\dfrac{\pi}{12}\ =\ \dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}\ =\ \dfrac{\sqrt{6}-\sqrt{2}}{4}\)☐
示例: 计算 \(\cos\dfrac{\pi}{12}\) 。
示例: 计算 \(\sin\dfrac{\pi}{12}+\cos\dfrac{\pi}{12}\) 。
解: 当然可以将前述题目的结果代入,此处展示另一种做法:
\(\left(\sin\dfrac{\pi}{12}+\cos\dfrac{\pi}{12}\right)^2=\sin^2\dfrac{\pi}{12}+\cos^2\dfrac{\pi}{12}+2\sin\dfrac{\pi}{12}\cos\dfrac{\pi}{12}\)
注意到:\(\sin\dfrac{\pi}{12}+\cos\dfrac{\pi}{12}>0\)
于是有:\(\sin\dfrac{\pi}{12}+\cos\dfrac{\pi}{12}=\sqrt{1+\sin\dfrac{\pi}{6}}=\dfrac{\sqrt{6}}{2}\)☐
示例: 使用两角和的三角函数公式,计算 \(\sin\dfrac{5\pi}{12}\) 和 \(\cos\dfrac{5\pi}{12}\) 。
(你计算的结果应该分别等于 \(\cos\dfrac{\pi}{12}\) 和 \(\sin\dfrac{\pi}{12}\))
使用前述倍角公式,可以得到以下正弦和余弦半角公式:1
半角的正弦和余弦
\(\sin\left(\dfrac{1}{2}x\right)=(-1)^{\lfloor x/(2\pi)\rfloor}\sqrt{\dfrac{1-\cos x}{2}}\)
\(\cos\left(\dfrac{1}{2}x\right)=(-1)^{\lfloor x+\pi/(2\pi)\rfloor}\sqrt{\dfrac{1+\cos x}{2}}\)
其中, \(\lfloor y\rfloor\) 表示小于等于实数 \(y\) 的最大整数。
思考与讨论
- 符号项 \((-1)^{\lfloor x/(2\pi)\rfloor}\) 和 \((-1)^{\lfloor x+\pi/(2\pi)\rfloor}\) 的意义何在?
- 你能说明这两个符号项的正确性么?
- 在实际计算中,应当如何确定符号项?
示例: 已知 \(\cos\dfrac{\pi}{12}=\dfrac{\sqrt{6}+\sqrt{2}}{4}\) ,计算 \(\sin\dfrac{\pi}{24}\) 和 \(\sin\dfrac{\pi}{24}\) 。
示例: 求值:\(\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}\)
解: \(\because\) \(\sqrt{2}=2\cos\dfrac{\pi}{4}\)
\(\therefore\) \(\sqrt{2+\sqrt{2}}=\sqrt{2(1+\cos\dfrac{\pi}{4})}=\sqrt{4\cos^2\dfrac{\pi}{8}}=2\cos\dfrac{\pi}{8}\)
\(\therefore\) \(\sqrt{2+\sqrt{2+\sqrt{2}}}=\sqrt{2(1+\cos\dfrac{\pi}{8})}=\sqrt{4\cos^2\dfrac{\pi}{16}}=2\cos\dfrac{\pi}{16}\)
\(\therefore\) \(\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}=\sqrt{4\cos^2\dfrac{\pi}{32}}=2\cos\dfrac{\pi}{32}\)☐
思考与讨论
- 我们已经讨论过角度为 \(\dfrac{\pi}{32},\ \dfrac{\pi}{24},\ \dfrac{\pi}{16},\ \dfrac{\pi}{12},\ \dfrac{\pi}{8},\ \dfrac{\pi}{6},\ \dfrac{\pi}{4},\ \dfrac{\pi}{3}\) 的三角函数,请整理表格列出这些角的正弦、余弦和正切值。
- 计算 \(\dfrac{\pi}{10},\ \dfrac{\pi}{5},\ \dfrac{2\pi}{5}\) (\(18^\circ,36^\circ,72^\circ\))的三角函数值。
提示:利用底角为 \(72^\circ\) 的等腰三角形的底角平分线
积化和差与和差化积公式
积化和差公式
\(\sin\alpha\cos\beta=\dfrac{1}{2}\left[\sin(\alpha+\beta)+\sin(\alpha-\beta)\right]\)
\(\cos\alpha\sin\beta=\dfrac{1}{2}\left[\sin(\alpha+\beta)+\sin(\alpha-\beta)\right]\)
\(\cos\alpha\cos\beta=\dfrac{1}{2}\left[\cos(\alpha+\beta)+\cos(\alpha-\beta)\right]\)
\(\sin\alpha\sin\beta=\dfrac{1}{2}\left[\cos(\alpha+\beta)-\cos(\alpha-\beta)\right]\)
和差化积公式
\(\sin\alpha+\sin\beta=2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}\)
\(\sin\alpha-\sin\beta=2\cos\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}\)
\(\cos\alpha+\cos\beta=2\cos\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}\)
\(\cos\alpha-\cos\beta=-2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}\)
\(\tan\alpha\pm\tan\beta=\dfrac{\sin(\alpha\pm\beta)}{\cos\alpha\cos\beta}\)
\(\cot\alpha\pm\cot\beta=\pm\dfrac{\sin(\alpha\pm\beta)}{\sin\alpha\sin\beta}\)
升幂公式
升幂公式是二倍角公式的变形,你需要“认得”这些变形。
升幂公式
\(1+\sin\alpha=\left(\sin\dfrac{\alpha}{2}+\cos\dfrac{\alpha}{2}\right)^2\)
\(1-\sin\alpha=\left(\sin\dfrac{\alpha}{2}-\cos\dfrac{\alpha}{2}\right)^2\)
\(1+\cos\alpha=2\cos^2\dfrac{\alpha}{2}\)
\(1-\cos\alpha=2\sin^2\dfrac{\alpha}{2}\)
三角形中的重要定理与常见恒等式
(吴家华 2021)- 第 9 页
正弦定理
\(\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}=2R\)
为了方便,在 \(\triangle{ABC}\) 中,三个内角分别为 \(A,B,C\) 其对应的边长分别为 \(a,b,c\) ,外接圆半径为 \(R\) 。
余弦定理
\(a^2=b^2+c^2-2bc\cos A\) \(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\)
\(\sin^2A=\sin^2B+\sin^2C-2\sin B\sin C\cos A\)
射影定理
\(a=b\cos C+c\cos B\)
正弦恒等式(一)
\(\sin2A+\sin2B+\sin2C=4\sin A\sin B\sin C\)
\(\dfrac{\cos A}{\sin B\sin C}+\dfrac{\cos B}{\sin C\sin A}+\dfrac{\cos C}{\sin A\sin B}=2\)
正弦恒等式(二)
\(\sin^2\dfrac{A}{2}+\sin^2\dfrac{B}{2}+\sin^2\dfrac{C}{2}=1-2\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2}\)
余弦恒等式
\(\cos^2A+\cos^2B+\cos^2C+2\cos A\cos B\cos C=1\)
\(\cos2A+\cos2B+\cos2C+4\cos A\cos B\cos C=-1\)
正切恒等式
\(\tan A+\tan B+\tan C=\tan A\tan B\tan C\) 其中 \(A,B,C\neq\dfrac{\pi}{2}\) \(\bigstar\)
\(\tan\dfrac{A}{2}\tan\dfrac{B}{2}+\tan\dfrac{B}{2}\tan\dfrac{C}{2}+\tan\dfrac{C}{2}\tan\dfrac{A}{2}=1\)
\(\bigstar\) \(A+B+C=k\pi\) 就有此结论。另外,反过来也成立:即如果\(\tan A+\tan B+\tan C=\tan A\tan B\tan C\) ,则 \(A+B+C=k\pi\)
余切恒等式
\(\cot\dfrac{A}{2}+\cot\dfrac{B}{2}+\cot\dfrac{C}{2}=\cot\dfrac{A}{2}\cot\dfrac{A}{2}\cot\dfrac{A}{2}\)
\(\cot{A}\cot{B}+\cot{B}\cot{C}+\cot{C}\cot{A}=1\)
\(a\sin\theta+b\cos\theta=\dfrac{1}{\sqrt{a^2+b^2}}\cdot(\cos\phi\sin\theta+\sin\phi\cos\theta)\)
\(=\sqrt{a^2+b^2}\cdot\sin(\theta+\phi)\)
其中 \(\cos\phi=\dfrac{a}{\sqrt{a^2+b^2}}\ ,\ \sin\phi=\dfrac{b}{\sqrt{a^2+b^2}}\)
示例: 将 \(\sin\theta+\sqrt{3}\cos\theta\) 化为单一角三角函数。
解: 注意到 \(1^2+\sqrt{3}^2=2^2\) ,于是有:
\(\sin\theta+\sqrt{3}\cos\theta=2\left(\dfrac{1}{2}\sin\theta+\dfrac{\sqrt{3}}{2}\cos\theta\right)=2\left(\cos\dfrac{\pi}{3}\sin\theta+\sin\dfrac{\pi}{3}\cos\theta\right)\)
因此,\(\sin\theta+\sqrt{3}\cos\theta=2\sin\left(\theta+\dfrac{\pi}{3}\right)\)☐
示例: 求 \(3\sin\theta-4\cos\theta\) 的最大值和最小值。
解: 注意到 \(3^2+4^2=5^2\) ,于是有:
\(3\sin\theta-4\cos\theta=5\left(\dfrac{3}{5}\sin\theta-\dfrac{4}{5}\cos\theta\right)=5\left(\cos\phi\sin\theta-\sin\phi\cos\theta\right)\)
其中,\(\phi\) 是边长为 \(3,4,5\) 的直角三角形较大的锐角
\(3\sin\theta-4\cos\theta=5\sin\left(\theta-\phi\right)\)
因此,\(3\sin\theta-4\cos\theta\) 的最大值为 \(5\) ,最小值为 \(-5\) 。☐
示例: 求函数 \(f(x)=x+\sqrt{1-x^2}\) 的最大值和最小值。
解: 注意到 \(x\in[-1,1]\) ,令 \(x=\sin\theta,\ \theta\in[-\dfrac{\pi}{2},\dfrac{\pi}{2}]\) ,于是有:
\(f(x)=\sin\theta+\cos\theta=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)\)
因此 \(f(x)\) 的最大值和最小值分别为 \(\sqrt{2}\) 和 \(-1\) 。☐
另解 (判别式法)令 \(a=x+\sqrt{1-x^2}\)
示例: 解方程 \(\sqrt{1-x^2}+x=\sqrt{2}\)
示例: 求 \(f(x)=\sqrt{x-1}+\sqrt{5-x}\) 的值域。
解: 令 \(t=\sqrt{x-1},\ t\in[0,2]\) 有:
\(f(x)=t+\sqrt{4-t^2},\ t\in[0,2]\)
至此问题转换为前述示例的类似形式。请补充后续步骤:
解: 注意到 \(\left(\sqrt{x-1}\right)^2+\left(\sqrt{5-x}\right)^2=4\) , \(\sqrt{x-1}\ge0,\ \sqrt{5-x}\ge0\)
令 \(\sqrt{x-1}=2\sin\theta,\ \sqrt{5-x}=2\cos\theta,\ \theta\in[0,\dfrac{\pi}{2}]\)
于是有 \(f(x)=2\sin\theta+2\cos\theta=2\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)\)
\(\theta+\dfrac{\pi}{4}\in[\dfrac{\pi}{4},\dfrac{5\pi}{2}]\) ,进一步 \(\sin\left(\theta+\dfrac{\pi}{4}\right)\in[\dfrac{\sqrt{2}}{2},1]\)
因此,\(f(x)\) 的值域为 \([2,2\sqrt{2}]\) 。☐
点评 本题是一类常见问题 \(x^2+y^2=k\) 求 \(x+y\) 的最值或值域。这类问题除了使用三角换元法外,还可以使用判别式法、解析几何法,这类问题还牵涉到均值不等式。请看接下来的示例。
示例: 已知 \(x^2+y^2=1\) ,求 \(x+y\) 的最值。
解: 令 \(x=\cos\theta,\ y=\sin\theta,\ \theta\in[0,2\pi)\)
\(x+y=\cos\theta+\sin\theta=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)\)
因此 \(x+y\) 的最大值是 \(\sqrt{2}\) ,最小值是 \(-\sqrt{2}\) 。☐
点评 这其实是圆的参数方程,联系如下图像:
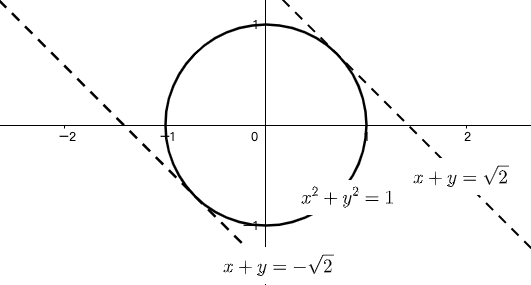
示例: 已知满足条件 \(x^2-2x+y^2=0\) 的任意实数 \(x,y\) 均能使不等式 \(x+y+k\ge0\) 恒成立,试求 \(k\) 的取值范围。
示例: 若实数 \(x\sqrt{1-y^2}+y\sqrt{1-x^2}=1\) ,求 \(x^2+y^2\) 的值。
按语 这是笔者在撰写本讲义时在 B 站也被推送到这道题目,以下是 UP 主的解答,是初中的基本方法。

除去这种“整体法换元去根号”的方法之外,本题使用三角函数换元更为便捷。另外还可以用向量内积或柯西-施瓦茨不等式进行解答。
解法一 三角换元原题:已知 \(x^2+y^2=1\) ,求 \(\sqrt{(x+1)^2+(y-1)^2}\) 的最值。
有内积就有柯西不等式
示例:2 已知实数 \(a,b\) 满足 \(a^2-ab+b^2=1\) ,求 \(f(a,b)=a^2+b^2\) 的值域。
解: [分析] 有些学生注意到已知可化成 \(\left(a-\dfrac{b}{2}\right)^2+\dfrac{3}{4}b^2=1\)
于是设 \[\begin{equation*} \begin{cases} a-\dfrac{b}{2}=\cos\theta\\ \\ \dfrac{\sqrt{3}}{2}b=\sin\theta \end{cases} \end{equation*}\]
即 \[\begin{equation*} \begin{cases} a=\dfrac{1}{\sqrt{3}}\sin\theta+\cos\theta\\ \\ b=\dfrac{2}{\sqrt{3}}\sin\theta \end{cases} \end{equation*}\]
代入 \(f(a,b)=a^2+b^2\) 得到:
\(f(a,b)=\left(\dfrac{1}{\sqrt{3}}\sin\theta+\cos\theta\right)^2+\left(\dfrac{2}{\sqrt{3}}\sin\theta\right)^2\)
然后进一步化简求解。但这样的做法比较麻烦。
若逆向考虑,设 \(a^2+b^2=R^2\ (R>0)\)
并设 \(a=R\cos\theta,\ b=R\sin\theta\) 代入已知等式得到:\[\sin2\theta=2-\dfrac{2}{R^2}\]
形式就简化很多。
解:示例:3 (第三届“希望杯”数学邀请赛试题)已知 \(\alpha,\beta\) 均为锐角,且 \(\dfrac{\cos^4\alpha}{\sin^2\beta}+\dfrac{\sin^4\alpha}{\cos^2\beta}=1\) ,求证:\(\alpha+\beta=\dfrac{\pi}{2}\)
示例:4 (1989年北京市奥林匹克学校高中入学试题)设实数 \(a,b,c,d\) 满足条件 \(a^2+b^2=c^2+d^2=1,\ ac+bd=0\) ,求 \(a^4+b^4+c^4+d^4-4abcd\) 的值。
解法一:(三角换元)示例:5 求 \(f(x)=2\sqrt{x^2+1}+x\) 的值域。
解法一 \(f(x)\) 的定义域为 \((-\infty,+ \infty)\) ,并且 \(f(x)\) 含 \(\sqrt{x^2+1}\) 项。
于是令 \(x=\tan\theta,\ \theta\in(-\dfrac{\pi}{2},+\dfrac{\pi}{2})\)
则 \(f(x)=2\sqrt{\dfrac{1}{\cos^2\theta}}+\tan\theta=\dfrac{2}{\cos\theta}+\dfrac{\sin\theta}{\cos\theta}=\dfrac{\sin\theta-(-2)}{\cos\theta-0}\)也可以利用关于 \(x\) 的方程 \(a\sin x+b\cos x + c = 0\) 有解的充分必要条件是:\(a^2+b^2\ge c^2\) 这一结论求解。
发现 \(f(x)\) 为点 \((\cos\theta,\sin\theta)\) 到 \((0,-2)\) 连线的斜率。
绘制如图 9 所示的图像,得到 \(f(x)\) 的值域为 \([\sqrt{3},+ \infty)\) 。☐
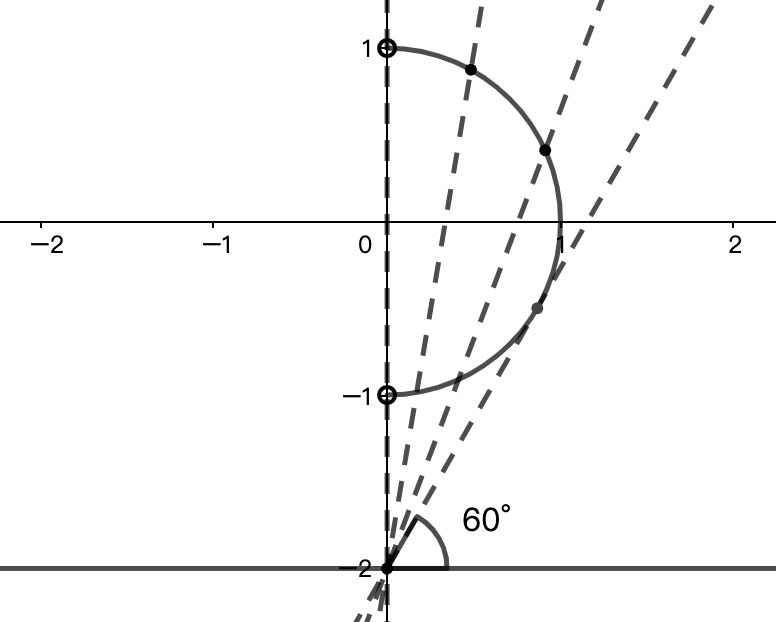
解法二 设 \(a=2\sqrt{x^2+1}+x\)
\(a-x=2\sqrt{x^2+1}\) 两边平方得:
\((a-x)^2=4(x^2+1)\) 其中 \(x\leq a\) 。整理得:
\(3x^2+2ax+4-a^2=0, \ x\leq a\)
根据题意,该方程在 \((-\infty,a]\) 区间内有根小心求解 \(\dfrac{-2a-\sqrt{16a^2-48}}{6}\leq a\)
\[\begin{equation*} \begin{cases} \Delta=16a^2-48\geq0\\ \\ \dfrac{-2a-\sqrt{16a^2-48}}{6}\leq a \end{cases} \Leftrightarrow \begin{cases} a\leq-\sqrt{3}\ or\ a\geq\sqrt{3}\\ \\ a\geq0 \end{cases} \Leftrightarrow a\geq\sqrt{3} \end{equation*}\]
因此 \(f(x)\) 的值域为 \([\sqrt{3},+ \infty)\) 。☐
这题其实求导立刻就做出来
示例:6 求方程 \(x\sqrt{y-1}+y\sqrt{x-1}=xy\) 的所有实数解。
解: 由原方程可知 \(x\leq1,\ y\leq1\)
设 \(x=\sec^2\theta,\ y=\sec^2\phi\) ,其中 \(\theta,\phi\in[0,\dfrac{\pi}{2})\)
原方程化为 \(\sec^2\theta\sqrt{\sec^2\phi-1}+\sec^2\phi\sqrt{\sec^2\theta-1}=\sec^2\theta\sec^2\phi\)
化简即得 \(\sin\phi\cos\phi+\sin\theta\cos\theta=1\)
即 \(\sin2\phi+\sin2\theta=2\)
上式仅当 \(\sin2\phi=\sin2\theta=1\) 成立。
于是可得原方程的解为 \(x=2,\ y=2\) 。☐
示例:9 求函数 \(f(x)=\dfrac{x-x^3}{1+2x^2+x^4}\) 的值域
解法一(三角函数代换)基础练习:任意角的三角函数
练习:10 将以下角度转换为三位小数的十进制度 (DD) 格式。
\(5^\circ51'33"\) (2) \(14^\circ18'37\)
\(354^\circ8'29"\) (4) \(184^\circ31'7"\)
练习:11 将以下角度转换为“度-秒-分” (DMS) 格式。
\(3.042^\circ\) (2) \(49.715^\circ\)
\(403.223^\circ\) (4) \(156.808^\circ\)
练习:12 在下面的 \(\square\) 里,填上适当的正负号或角度。
\(\sin(-390^\circ)=\square\sin390^\circ=\square\sin(30^\circ+360^\circ)=\square\sin\square\)
\(\cos(-750^\circ)=\square\cos750^\circ=\square\cos(30^\circ+360^\circ\times2)=\square\cos\square\)
\(\tan(-1100^\circ)=\dfrac{\sin(-1100^\circ)}{\cos(-1100^\circ)}=\dfrac{\square\sin(20^\circ+360^\circ\times3)}{\square\cos(20^\circ+360^\circ\times3)}=\square\dfrac{\sin\square}{\cos\square}=\square\tan\square\)
练习:13 下列各角是第几象限角?
- \(2000^\circ\)(2) \(-4000^\circ\)
练习:14 下列各角是第几象限角?
\(370^\circ\)(2) \(420^\circ\)(3) \(\dfrac{7}{3}\pi\)(4) \(-40^\circ\)
\(-100^\circ\)(6) \(-365^\circ\)(7) \(-750^\circ\)(8) \(-\dfrac{5}{2}\pi\)
练习:15 下列各角是第几象限角?
\(290^\circ\)(2) \(160^\circ\)(3) \(255^\circ\)(4) \(-110^\circ\)
\(570^\circ\)(6) \(-420^\circ\)(7) \(-660^\circ\)(8) \(1120^\circ\)
练习:16 求下列各式的值:
\(\cos570^\circ\sin150^\circ+\sin(-330^\circ)\cos(-390^\circ)\)
\(\cos420^\circ\tan60^\circ\sec45^\circ+\sin45^\circ\cot30^\circ\csc450^\circ\)
练习:17 求下列各式的值:
\(\cot10^\circ+\tan190^\circ+\tan100^\circ+\tan350^\circ\)
\(\sin1590^\circ\cos(-1860^\circ)+\tan1395^\circ\cot(-960^\circ)\)
练习:18 将下列函数表示为 \(x\) 的三角函数:
\(\cos(-x)\)(2) \(\sin(x-\dfrac{\pi}{2})\)(3) \(\cos(\dfrac{\pi}{2}+x)\)
\(\tan(\pi-x)\)(5) \(\sin(\pi+x)\)
练习:19 将 \(A-90^\circ\) 和 \(A-180^\circ\) 的各三角函数表示为 \(A\) 的三角函数。
练习:20 当 \(\theta\) 是第四象限的角, \(\cos\theta=\dfrac{12}{13}\) 时, \(\sin\theta\) 和 \(\tan\theta\) 的值各是多少?
练习:21 若 \(\theta\) 是第三象限的角, \(2\sin\theta=\cos\theta\) ,求 \(\sin\theta\) 、 \(\cos\theta\) 和 \(\tan\theta\) 的值。
练习:22 比较任意角 \(A\) 和 \(-A\) 的正弦、余弦和正切的三角函数值。即判断正弦、余弦和正切函数的奇偶性。
练习:23 将 \(\sin(90^\circ+\theta)\) 、 \(\cos(\theta-90^\circ)\) 、 \(\tan(180^\circ-\theta)\) 写成 \(\theta\) 的三角函数。
练习:24 证明下面两个式子成立:
\(\sin(180^\circ+\theta)+\cos(90^\circ-\theta)=0\)
\(\cos(270^\circ-\theta)-\cos(\theta+90^\circ)=0\)
练习:25 将以下各三角函数值按大小次序排列:
\(\sin870^\circ,\ \cos(-450^\circ),\ \tan1310^\circ,\ \sin(-2095^\circ),\ \cos1900^\circ\)
练习:26 若 \(\sin B=\sin A\) 且 \(\cos A=\cos B\) ,证明 \(A,B\) 是终边相同的角,即 \(A-B\) 是 \(0^\circ\) 或 \(360^\circ\) 的倍数。
练习:27 若 \(\theta\) 是锐角, \(\sin\theta-\cos\theta=\dfrac{1}{2}\) ,求下列各式的值。
- \(\sin\theta\cos\theta\)(2) \(\sin\theta+\cos\theta\)(3) \(\sin^3\theta-\cos^3\theta\)
练习:28 化简下面的算式:
\(\dfrac{\sin(\pi+\theta)\tan^2(\pi-\theta)}{\cos\left(\dfrac{3}{2}\pi+\theta\right)}-\dfrac{\sin\left(\dfrac{3}{2}\pi-\theta\right)\csc^2\left(\dfrac{\pi}{2}+\theta\right)}{\sin\left(\dfrac{\pi}{2}+\theta\right)}\)
练习:29 \(0^\circ<\theta<360^\circ\),
适合 \(\sin\theta=\dfrac{1}{2}\) 的 \(\theta\) 值是多少?
适合 \(\cos\theta=-\dfrac{1}{\sqrt{2}}\) 的 \(\theta\) 角在第几象限?
练习:30 求下列两式的值:
\(\tan\dfrac{5\pi}{6}\cos\dfrac{3\pi}{4}+\tan\dfrac{2\pi}{3}\cot\dfrac{21\pi}{4}\)
\(\cot\dfrac{\pi}{3}\tan\dfrac{5\pi}{6}+\sin\dfrac{31\pi}{4}\cos\dfrac{13\pi}{3}\)
练习:31 当 \(\cos(-100^\circ)=k\) 时,用 \(k\) 表示 \(\tan80^\circ\)
练习:32 化简下列两式:
\(\tan(180^\circ+\theta)\sin(90^\circ+\theta)+\dfrac{\cos(180^\circ-\theta)}{\tan(180^\circ-\theta)}\)
\(\dfrac{\sin(180^\circ+\theta)\tan^2(180^\circ-\theta)}{\cos(270^\circ+\theta)}-\dfrac{\sin(270^\circ-\theta)}{\sin(90^\circ+\theta)\cos^2\theta}\)
练习:33 用 \(\cos\theta\) 表示 \(1+\tan^4\theta\)
练习:34 若 \(\tan\theta=-\dfrac{4}{3}\) ,求 \(\dfrac{5\sin\theta+8}{15\cos\theta-7}\)
练习:35 用 \(\tan A\) 表示 \(\sin^6A+\cos^6A\)
练习:36 如果将三角形 \(ABC\) 的三个内角用 \(A\)、\(B\)、\(C\) 表示,则 \(A+B+C=180^\circ\) 。以此说明下列各等式成立:
\(\sin(B+C)=\sin A\)
\(\tan(B+C)=-\tan A\)
\(\sin\dfrac{B+C}{2}=\cos\dfrac{A}{2}\)
\(\cos\dfrac{B+C}{2}=\sin\dfrac{A}{2}\)
\(\sin A=-\sin(2A+B+C)\)
练习:37 求下列函数的周期、最大值和最小值:
\(\tan2x\)(2) \(\sin^2 x\)(3) \(|\sin x|\)
\(\cos3x\)(5) \(\dfrac{1}{1+\sin2x}\)(6) \(\dfrac{1}{1+\tan^2x}\)
练习:38 求 \(\cos570^\circ\sin510^\circ-\sin330^\circ\cos390^\circ\) 的值。
练习:39 把下列各三角函数化成小于 \(45^\circ\) (或 \(\dfrac{\pi}{4}\) )的正角的三角函数。
\(\sin740^\circ\)(2) \(\cos(-300^\circ)\)(3) \(\cot\left(-\dfrac{1}{3}\pi\right)\)
\(\csc1120^\circ\)(5) \(\csc(-60^\circ)\)
练习:40 求 \(0^\circ\) 至 \(900^\circ\) 间所有适合 \(\tan\theta=1\) 的角 \(\theta\) 。
练习:41 求 \(0^\circ\) 至 \(900^\circ\) 间所有适合 \(\cos^2\theta=\dfrac{1}{2}\) 的角 \(\theta\) 。
基础练习:三角函数的图像
练习:42 画 \(y=\sin\theta\) 和 \(y=\cos\theta\) 的图像。

练习:43 画 \(y=\tan\theta\) 和 \(y=\cot\theta\) 的图像。

练习:44 画 \(y=\sec\theta\) 和 \(y=\csc\theta\) 的图像。

练习:45 当 \(a,b\) 都是非 \(0\) 实数时,证明下列两个函数的图像可以经平移后重合: \[y=a\sin x+b\cos x\qquad\textcircled{1}\] \[y=a\sin x-b\cos x\qquad\textcircled{1}\]
练习:46 图 10 是 \(y=R\cos\left(\dfrac{2\pi}{3}x+\theta\right)-1\) 的图像的一部分,求 \(R\) 、 \(\theta\) 和 \(a\) 的值。(其中 \(R\) 是正数,角用弧度制表示)
练习:47 把 \(y=\sin x\) 的图像:
向上平移 \(5\) 个单位,方程有何变化?
向左平移 \(90^\circ\) ,方程如何变化?
化简 (2) 中所得到的方程。
练习:48 画出函数 \(y=\ln(1+\sin x),\ -360^\circ\leq x\leq360^\circ\) 图像的大体形状。

练习:49 画出下列函数的图像:
\(y=|\cos x|\)
\(y=|\cos x|+\cos x\)
\(y=|\cos x|=\cos x\)

练习:50 画出下列函数的图像:
\(y=\sin|x|\)
\(y=\sin|x|+\sin x\)

练习:51 函数 \(y=\dfrac{1}{2}\cos(3x-120^\circ)+1\) 的周期、初始相位、零点和极值点都是什么?并绘制其图像。

练习:52 函数 \(y=\sin^2 x\) 的周期是什么,绘制其图像。

参考答案是强行分析,更好的方法是先对函数表达式进行恰当变形
练习:54 当 \(\theta\) 从 \(0\) 到 \(2\pi\) 变化时, \(\cos\theta-\sin\theta\) 的符号和值如何变化?
练习:55 求 \(\sin\left[\dfrac{n\pi}{2}+(-1)^n\dfrac{\pi}{6}\right]\) 所有可能的值,其中 \(n\) 为 \(0\) 或任意正整数。
练习:56 假设图 11 中的波形曲线用 \(y=a+b\cos\theta+c\cos2\theta\) 表示。试从图中读取一些适当的数据,从而确定 \(a,b,c\) 的值。
练习:57 分析函数 \(y=\sin x+\dfrac{1}{2}\sin2x\) 的零点、单调区间、极值点、凹凸性,并绘制函数图像。

练习:58 画出下列函数的图像:
\(y=\sin\left(x+\dfrac{\pi}{4}\right)\)
\(y=\cos\left(x-\dfrac{\pi}{2}\right)\)
\(y=\tan\left(\dfrac{\pi}{4}-x\right)\)


基础练习:两角和与差的三角函数
练习:59 求 \(\sin100^\circ\sin(-160^\circ)+\cos200^\circ\cos(-280^\circ)\) 的值。练习:60 求 \(\sin^6\theta+\cos^6\theta\) 的最大值和最小值。并求取到最值时 \(\theta\) 的值。
练习:61 \(A\) 为锐角,当 \(\sin A=\dfrac{3}{5}\) 时,求 \(\tan\dfrac{A}{2}\) 的值。
练习:62 \(180^\circ<A<360^\circ\) ,\(\cos A=\dfrac{1}{\sqrt{2}}\) ,求 \(\sin\dfrac{A}{2}\) 的值。
练习:63 \(180^\circ<A<540^\circ\) , \(\cos A=-\dfrac{1}{2}\) ,求 \(\cos\dfrac{A}{2}\) 的值。
练习:64 \(\tan A=\dfrac{1}{2},\ \tan B=\dfrac{1}{3}\) 时,求 \(\sin(A-B)\) 的值。
练习:65 已知 \(\sin\theta+\cos\theta=\sqrt{2}\) ,求 \(\sin\theta,\ \cos\theta,\ \tan\theta\) 的值。
练习:66 已知 \(\cos A=\dfrac{4}{5},\ \cos B=\dfrac{3}{5}\) ,求 \(\sin(A+B)\) 和 \(\cos(A-B)\)
练习:67 当 \(\theta\) 从 \(0^\circ\) 变到 \(360^\circ\) 时,研究 \(\dfrac{1-\cos\theta}{1+\cos\theta}\) 的单调性。
练习:68 证明 \(\dfrac{1-\cos2A}{1+\cos2A}=\tan^2A\)
练习:69 证明 \(\dfrac{1+\cos A}{\sin A}=\cot\dfrac{1}{2}A\)
练习:70 证明 \(\dfrac{\cos(A+B)+\cos(A-B)}{\cos(A-B)-\cos(A+B)}=\cot A\cot B\)
练习:71 证明 \(\dfrac{1}{\sqrt{2}}(\cos A+\sin A)=\sin(\dfrac{\pi}{4}+A)=\sin(\dfrac{3\pi}{4}-A)\)
练习:72 若 \(\sin A=\sin B,\ \cos A=\cos B\) ,证明 \(A,B\) 是终边相同的角。
练习:73 \(A,B\) 均为锐角, \(\sin A=\dfrac{13}{14},\ \sin B=\dfrac{11}{14}\) ,求 \(\sin(A+B)\) ,并指出 \(A+B\) 的具体角度。
练习:74 \(A,B\) 是锐角, \(3\sin^2A+2\sin^2B=1,\ 3\sin2A-2\sin2B=0\) ,证明这时 \(A+2B=90^\circ\) 。
练习:75 证明:\(\cos3\theta=4\cos^3\theta-3\cos\theta\)
练习:76 \(\theta=18^\circ\) ,证明:\(\sin2\theta=\cos3\theta\) ,并由此求出 \(\sin18^\circ\) 的值。
练习:77 证明:\(\cos20^\circ+\cos100^\circ+\cos140^\circ=0\)
练习:78 若 \(\tan A=\dfrac{1}{2},\ \tan B=\dfrac{1}{3}\) ,求 \(\tan(A+B)\) 的值。
练习:79 若 \(\tan\alpha=\dfrac{m}{m+1},\ \tan\beta=\dfrac{1}{2m+1}\) ,证明 \(\tan(\alpha+\beta)=1\) 。
练习:80 若方程 \(ax^2+bx+c=0\) 的两个根是 \(\tan A,\ \tan B\) ,求 \(\tan(A+B)\) 的值。
练习:81 若 \(\alpha+\beta=45^\circ\) ,证明:\((1+\tan\alpha)(1+\tan\beta)=2\)
基础练习:解三角函数方程
练习:82 解方程 \(\sin6x-2\sin4x+\sin2x=0\)
练习:83 解方程 \(\sin^2 x+\sin^2 2x=\sin^2 3x\)
练习:84 解方程 \(\cos x\cos3x=\cos5x\cos7x\)
练习:85 解方程 \(\tan x+\tan3x=2\tan2x\)
练习:86 \(0\leq x\leq\pi\) ,解方程 \(\sin x+\sin2x+\sin3x=0\)
练习:87 解方程 \(a\sin x+b\cos x=c\) ,其中 \(ab\neq0\)
练习:88 确定能使 \(\sin^2 x+\cos x+a=0\) 有解的 \(a\) 的范围。设 \(a=1\) ,解这个方程。
基础练习:三角函数换元法
练习:90 若 \(x\sqrt{1-y^2}+y\sqrt{1-x^2}=1\) ,求 \(x+y\) 的取值范围。
练习:98 求函数 \(f(x)=2\sqrt{x+1}+\sqrt{6-x}\) 的值域。