三角形的面积和比例
比的定义
比的定义
两个数量 \(a,b\) 的比记作 \(a:b\) ,意思是两个数量相除。相除的结果称为比值。 \(a\) 称为前项, \(b\) 称为后项。
将比例的前项和后项同时乘以或除以一个非零的数量,比值不变。比的前项和后项互质时,称为最简比。
也往往使用分数记号来表示两个数量的比,即 \(a:b=\dfrac{a}{b}\)
显然,比的后项不能为 \(0\) 。
示例: 一个数是 \(2\) ,另一个数是 \(5\) ,则两个数的比记作 \(2:5\) ,比值是 \(0.4\) 。可以写做: \[2:5=2\div5=0.4\]
相同量纲数量之比
两个数量的量纲如果相同(长度对长度、重量对重量就叫量纲相同),则两个数量的比值是一个没有量纲的数。
示例: 两条线段的长度分别为 \(50\mathrm{cm}\) 和 \(100\mathrm{cm}\) ,将其长度之比化为最简比如下: \[50\mathrm{cm}:100\mathrm{cm}=50:100=1:2\]
人们往往不严谨地称上述情形为“单位相同的数量之比”,但其实相同量纲的不同单位,其比值也是一个无量纲的数。
示例: 两条线段的长度分别为 \(50\mathrm{cm}\) 和 \(1\mathrm{m}\) ,其长度之比如下:\[50\mathrm{cm}:1\mathrm{m}=1:2\]
量纲相同的数量之比,往往反映了倍数关系。使用比的记号而不是除法来表示数量之间的关系时,传递的含义是我们关心这些数量的倍数关系而非具体值。
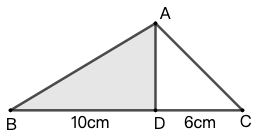
示例: 如图 所示, \(\triangle{ACD}\) 和 \(\triangle{ABD}\) 有公共顶点 \(A\) ,对应的底边 \(CD\) 和 \(BD\) 共线。因此二者的面积之比等于底边之比: \[S_{\triangle{ACD}}:S_{\triangle{ABD}}=BD:CD=6cm:10cm=3:5=0.6\]
三个或更多数量的比
比还可以用来表示三个或更多数量的倍数关系,这时无法使用分数记号或除号来表示,也没有所谓“三个数的比值”。这恰恰是比号的独特之处。
示例: 三条线段的长度分别为 \(50\mathrm{cm}\) ,\(100\mathrm{cm}\) 和 \(200\mathrm{cm}\) ,其长度之比可以写成:\[50\mathrm{cm}:100\mathrm{cm}:200\mathrm{cm}=1:2:4\]
思考与讨论
- 请使用两个数的比或除法,给出三个数的比的定义。
- 三个数的比,可以出现为 \(0\) 的项么?
比例
比例的定义
比例是表示两个或多个比相等的式子。例如 \(4:5=16:20\)。
四个数能组成上述等式,则称这四个数成比例。
靠近等号的两个数量称为比例的内项,如上述的 \(5\) 和 \(16\) 。远离等号的两个数量称为比例的外项,如上述的 \(4\) 和 \(20\) 。
比例的性质
对于成比例的四个数 \(a:b=c:d\) ,有如下性质:
性质: 比例的内项之积等于外项之积。即:\[b\cdot c=a\cdot d\]
性质: 当\(a,c\neq0\) 时,前项之比等于后项之比。即:\[a:c=b:d\]
性质: 和与差(差不为 \(0\) )依然成比例,即: \[a\pm c:b\pm d=a:b=c:d\]
思考与讨论
- 请尝试举出几个上述性质的例子。
- 如何证明上述性质?
图形的比例
面积和底边的关系
定理: 等高的三角形或平行四边形,它们面积的比等于它们底边的长度之比。 (Euclid VI.1)
平行线截线段成比例
定理: 做一条线段平行于三角形的一边,这条线段会将该三角形的另外两条边成比例分割。若将三角形的两条边成比例分割,则连接分割点所形成线段将平行于该三角形的另一条边。 (Euclid VI.2)
角平分线定理
定理: 若一条线段将三角形的一角均分为两份,该角平分线将底边分得的线段之比,等于三角形另两边之比。若三角形底边分割所得的线段之比等于另两端之比,那么,分割点与顶点间的连线平分三角形的这个角。 (Euclid VI.3)
相似三角形判定定理
定理: 在各角对应相等的三角形中,夹等角的边成比例,且等角的对边为相对应的边。(AAA) (Euclid VI.4)
定理: 若两个三角形的边成比例,那么这两个三角形的各角对应相等,对应边所对的角相等。(SSS) (Euclid VI.5)
定理: 若在两个三角形中有一个角彼此相等,且夹该等角的边成比例,那么这两个三角形的各角对应相等,且对应边所对的角相等。(SAS)(Euclid VI.6)
定理: 若在两个三角形中一对角相等,且夹另外两个角的边对应成比例,其余的那两个角都小于或都不小于直角,那么这两个三角形的各角对应相等,且成比例的边所夹的角也相等。(ASS)(Euclid VI.7)
射影定理
定理: 若在直角三角形中,由直角顶点向底边做垂线,垂线两侧的两个三角形与原三角形相似,且它们两个也彼此相似。 (Euclid VI.8)
定理: 推论:(射影定理/欧几里得定理)若在直角三角形中,由直角顶点向底边做垂线,这条垂线即为底边两部分的比例中项。
利用三角形面积推导比例关系
共边定理
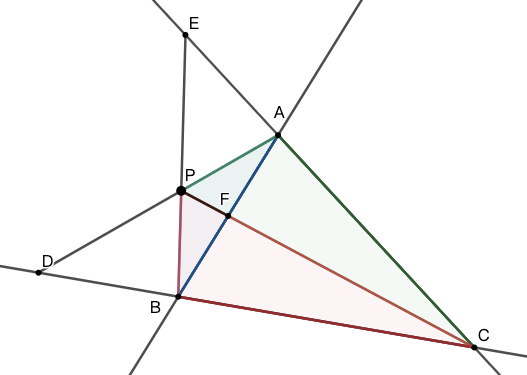
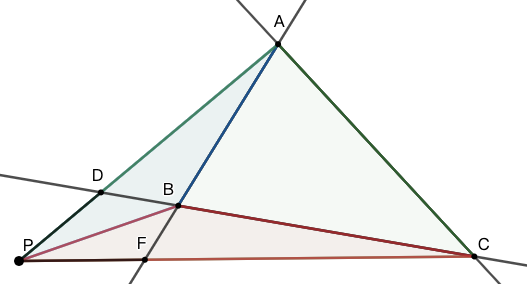
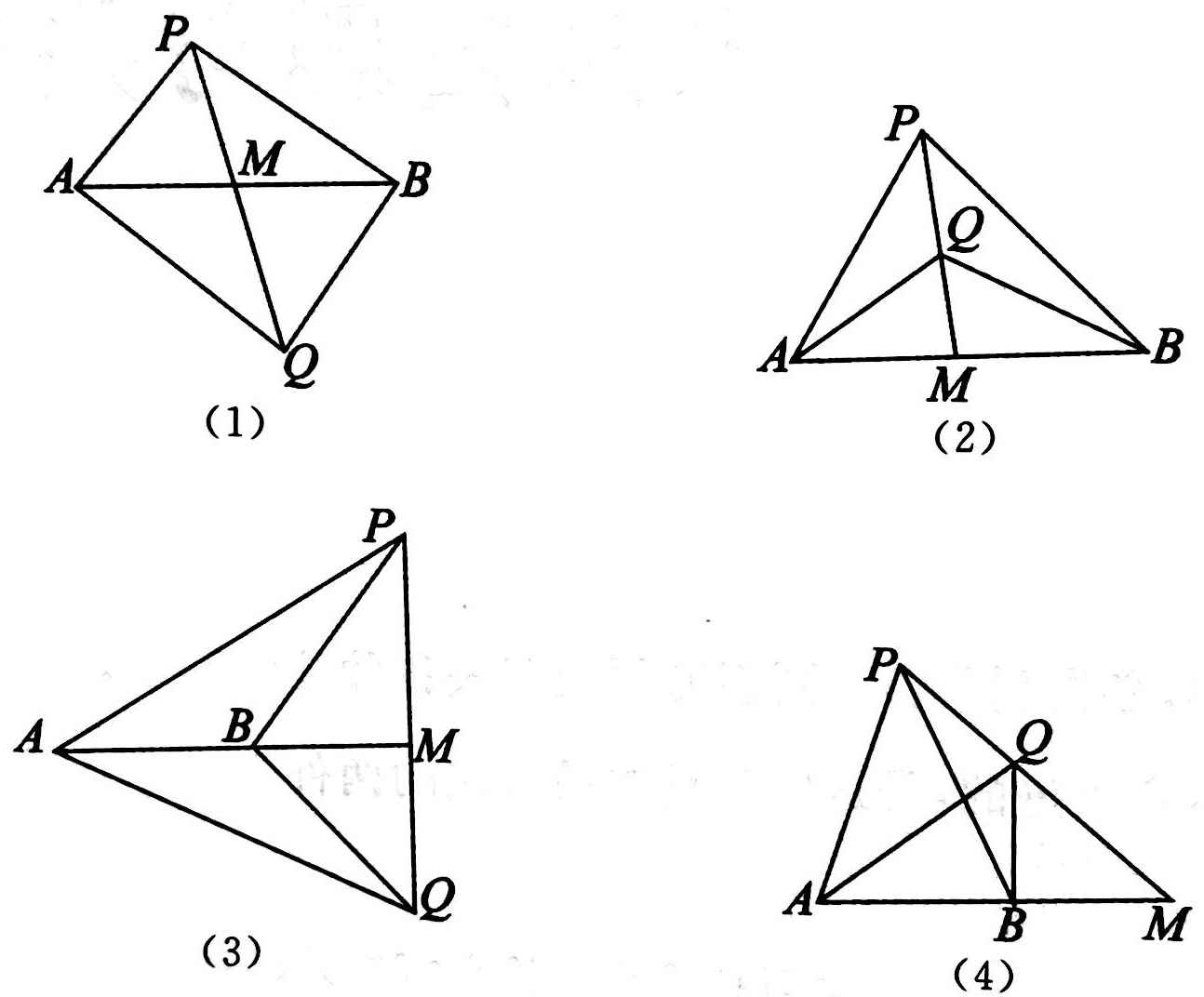
若两直线 \(AB\) 与 \(PQ\) 相交于 \(M\) ,如图 2,则:\[\dfrac{\triangle{PAB}}{\triangle{QAB}}=\dfrac{PM}{QM}\]
请注意,这可能有如图 2 所示的四种情况。其中的第 \(3,4\) 种情况在解题中并不容易看出来。
共角定理
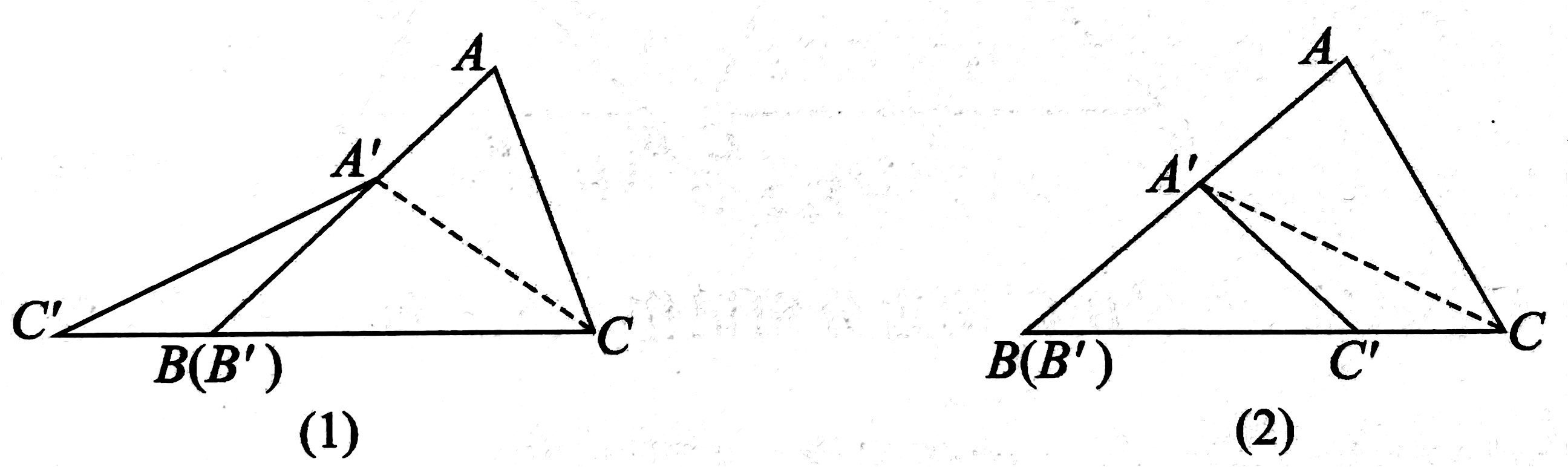
如果两个三角形的一个角相等或互补,就称它们是一对共角三角形,如图 3 所示。
共角三角形的面积之比,等于对应角(相等角或互补角)的两夹边乘积之比。也就是说,若 \(\angle{ABC}\) 与 \(\angle{A'B'C'}\) 相等或互补,则 \[\dfrac{\triangle{ABC}}{\triangle{A'B'C'}}=\dfrac{AB\cdot BC}{BC\cdot B'C'}\]
消点法
消点法是利用面积法解题时构建求解思路的一种通法。其基本思想是将“未知点”用“已知点”表示。
示例: 在矩形 \(ABCD\) 中 \(E\) 是 \(AB\) 的中点,\(CE\) 与 \(BD\) 交于点 \(F\) 。求 \(F\) 分 \(BD\) 和 \(CE\) 的比例,即 \(\dfrac{DF}{FB}\) 和 \(\dfrac{CF}{FE}\) 。
解: 观察图形的创建过程,我们注意到 \(A,B,C,D,E\) 的位置是给定的,所以我们要想办法将 \(F\) 用 \(A,B,C,D,E\) 表示出来。风筝模型可以将四边形对角线中点分线段的比例表示为顶点不含中点的大三角形的面积之比(如图 5 所示),即:\[\dfrac{DF}{FB}=\dfrac{\triangle{DCE}}{\triangle{BCE}}\]
注意观察上述比例关系的等式右边已经不包含点 \(F\) 。
其中 \(\triangle{DCE}=\dfrac{1}{2}S_{ABCD}\) , \(\triangle{BCE}=\dfrac{1}{4}S_{ABCD}\)
从而得到 \(\dfrac{DF}{FB}=2\) ,同理 \(\dfrac{CF}{FE}=\dfrac{\triangle{CBD}}{\triangle{EBD}}=2\) 。☐
思考与讨论
上述问题中,如果 \(ABCD\) 变为平行四边形,结论如何?变为梯形结论又如何?
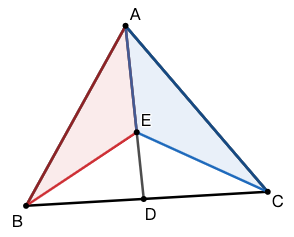
示例: 如图 6 所示,\(D\) 是 \(\triangle{ABC}\) 边 \(BC\) 上一点, \(E\) 是 \(AD\) 上一点。求证:\(S_{\triangle{AEB}}:S_{\triangle{AEC}}=BD:CD\) 。
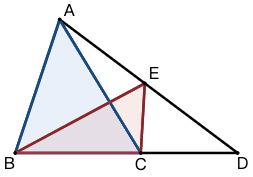
示例: 如图 7 所示,求证:\(S_{\triangle{ABC}}:S_{\triangle{EBC}}=AD:ED\) 。
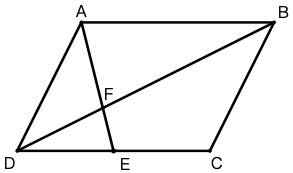
示例: 如图 8 所示,在平行四边形 \(ABCD\) 中, \(E\) 是 \(CD\) 中点,求 \(AF:FE\) 的值。
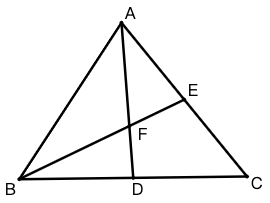
示例: 如图 9 所示,在 \(\triangle{ABC}\) 中, \(D\) 是 \(BC\) 中点, \(E\) 是 \(AC\) 中点。 求 \(AF:FD\) 的值。
思考与讨论
- 在上述题目中,利用面积法解题是如何一步一步消去未知量的?
- 你能将上述题目的条件一般化,从而得出 \(F\) 点分线段比例的公式么?
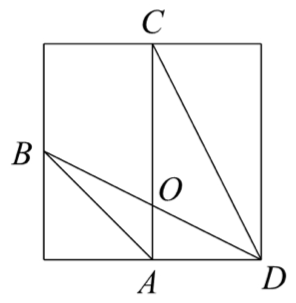
示例: (创新\(\cdot\)课堂练习$$06)如图 10 所示的正方形中(矩形也可以), \(A,B,C\) 分别是所在边的中点。求 \(S_{\triangle{COD}}:S_{\triangle{AOB}}\) 的值。
示例: (平行线截线段成比例)已知 \(\triangle{ABC}\) ,又有直线 \(DE\) 平行于 \(BC\) 且分别交 \(AB,AC\) 所在直线于 \(D,E\) 。
求证:\(AD:AB=AE:AC\) 。注意题目描述的图有几不同的情况
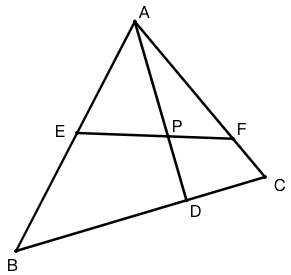
示例: \(\triangle{ABC}\) 三边上 \(BC,AC,AB\) 上各有点 \(D,E,F\) 。在已知 \(D,E,F\) 分各边的比例时,如何计算 \(AD\) 与 \(EF\) 交点分二者的比例?
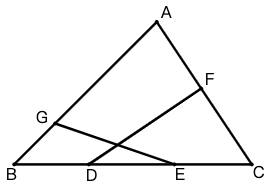
示例: \(\triangle{ABC}\) 三边上 \(BC\) 上有点 \(D,E\) ,\(AC,AB\) 上各有 \(F,G\) 。在已知 \(D,E,F,G\) 分各边的比例时,如何计算 \(GE\) 与 \(DF\) 交点分二者的比例?
梅涅劳斯定理
梅涅劳斯(Menelaus)定理最早出现在由古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica)中。梅涅劳斯定理描述了平面上四条直线处于“普通”位置时(既不平行,也没有三线共点)的线段比例关系。
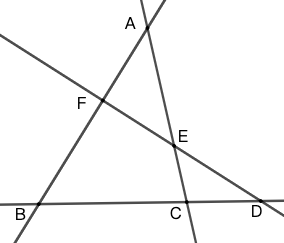
梅涅劳斯定理
当一条直线交 \(\triangle{ABC}\) 的三边 \(BC,\ AC,\ AB\) 所在直线分别于点 \(D,E,F\) 时,有:\[\dfrac{AF}{FB}\cdot\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}=1\]
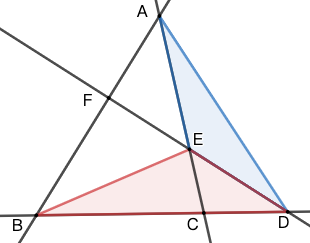
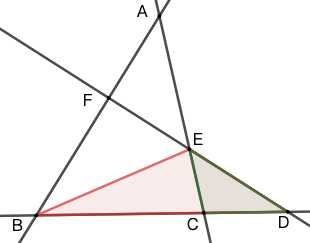
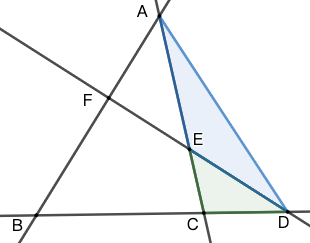
示例: 在图 13 中证明梅涅劳斯定理。
示例: 当梅涅劳斯定理所叙述的“直线 \(DEF\)”交 \(\triangle{ABC}\) 的三边于其延长线时,画出该图形,并且证明梅涅劳斯定理仍然成立。
示例: 在 \(\triangle{ABC}\) 中,\(D\) 为 \(BC\) 上靠近 \(B\) 的三等份点, \(E\) 为 \(AC\) 上靠近 \(A\) 的三等分点。连接 \(AD\) , \(BE\) 交于点 \(F\) 。绘制该图形,并计算 \(F\) 分别分 \(AD\) 和 \(BE\) 的比例。
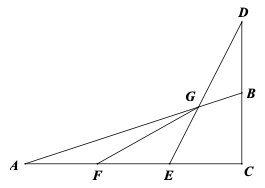
示例: (创新\(\cdot\)课堂练习$\(01)如图 15 所示,\)=90^$, \(AF=FE=EC=3\) , \(CB=BD=4\) 。
(1)求 \(DG:GE\) 和 \(AG:GB\) 的值。
(2)求该图形的面积。
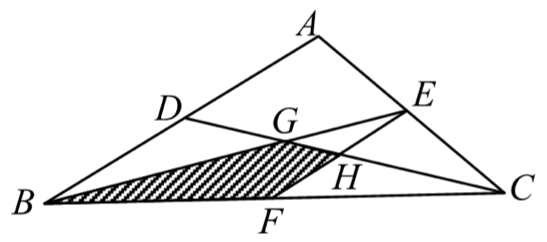
示例: (小优\(\cdot\)课堂练习$$04)如图 16 所示, \(D\) 为 \(AB\) 中点, \(E\) 为 \(AC\) 中点, \(F\) 为 \(BC\) 中点。
(1)求 \(CD\) ,\(BE\) , \(EF\) 被 \(G,H\) 所分的比例。
(2)求阴影部分的面积与 \(\triangle{ABC}\) 的面积之比。
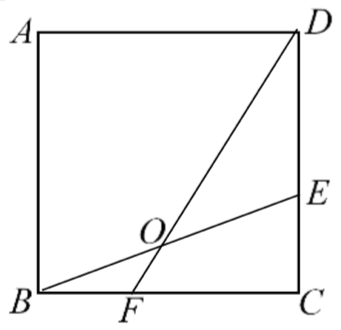
示例: (创新\(\cdot\)课堂练习$$05)如图 17 所示,正方形 \(ABCD\) 的边长是 \(12\) , \(BF=CE=4\) 。
(1)求 \(BO:OE\) 和 \(DO:OF\) 的值。
(2)求四边形 \(ABOE\) 的面积。
塞瓦定理
塞瓦定理
塞瓦线段是各顶点与其对边或对边延长线上的一点连接而成的直线段。塞瓦定理(英语:Ceva’s theorem)指出:如果\(\triangle ABC\)的塞瓦线段\(AD\) 、\(BE\)、\(CF\) 通过同一点 \(O\),则 \[\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}\cdot\dfrac{AF}{FB}=1\]
它的逆定理同样成立:若D、E、F分别在 \(\triangle ABC\) 的边 \(BC\) 、 \(CA\) 、 \(AB\) 或其延长线上(都在边上或有两点在延长线上),且满足 \[\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}\cdot\dfrac{AF}{FB}=1\]
则直线\(AD\)、\(BE\)、\(CF\)共点或彼此平行(于无限远处共点)。当\(AD\)、\(BE\)、\(CF\)中的任意两直线交于一点时,则三直线共点;当\(AD\)、\(BE\)、\(CF\)中的任意两直线平行时,则三直线平行。
(出自中文维基百科《塞瓦定理词条》)
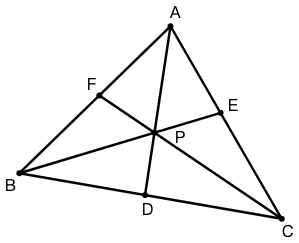
示例: 利用面积法,在图 18 中证明塞瓦定理。
示例: 利用梅涅劳斯定理,在图 18 中证明塞瓦定理。
示例: 请注意:塞瓦定理的三条塞瓦线在三角形外时,定理也成立。请用以下两个示意图验证塞瓦定理的证明