三角形的面积
导言
三角形的面积公式是小学阶段几何的核心,在中学的几何体系中也非常重要。在很多棘手的问题上,如果能够灵活地运用三角形面积的性质,往往可以收到奇效。
可以想象人类最初一定是直观地认识了正方形、长方形、平行四边形、三角形以及梯形等简单图形的面积。在小学三年级至五年级的课本上,我们也用类似的方法认识了图形的面积。
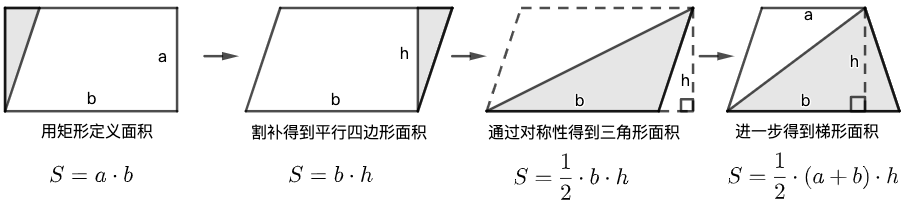
人类从观察中提炼出各种各样的知识之后,下一步就是把这些知识以某种形式组织起来。数学家从观察到的性质中精心挑选了一组基础的命题,再运用基本的逻辑原则,逐步推导出所有的性质。随着数学的进一步发展,这些“基础的命题”不一定是从观察中得到,某些尚未被观察或证实的“假设”也可以作为逻辑推理的基石。
从尽可能少的定义和不加证明的命题(公理)出发,通过演绎推理,得到整个理论体系,这就是“公理化方法”。这是一种组织已有知识的方法。在公理化体系中,有些命题比较基本,另一些命题由之推导而出。在《几何原本》中,“全等三角形”是相当基本的命题,平行四边形的性质是用全等三角形证明的。有了平行四边形的各种性质之后,三角形的面积定理才被证明出来。
三角形面积公式
三角形面积定理是小学数学中的核心定理。许多定理和题目都是以三角形的面积公式为出发点进行推导和求解。三角形的面积是由平行四边形面积的一半得到的。我们先证明以下性质:
三角形和平行四边形的面积关系
定理: 如果平行四边形和三角形既同底又在相同的平行线之间,那么平行四边形的面积是三角形的两倍。 (Euclid I.41)
三角形面积公式
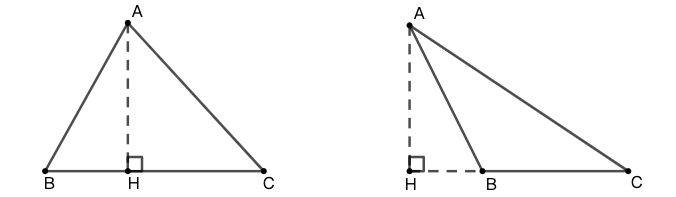
从顶点向底边所在直线引垂线段,这条线段称为三角形该底边上的的高 ,如图 3 所示。三角形的面积 \(S\) 的基本公式如下,其中 \(b\) 是底边的长度,\(h\) 是底边上高的长度。\[S=\dfrac{1}{2}\cdot b\cdot h\] 即:三角形的面积等于底乘高除以二。
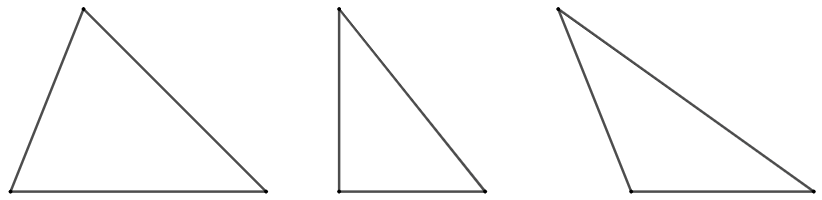
示例: 做出以下每个三角形三条底边上的高。
示例: 图 5 所示的大长方形面积为 \(100cm^2\) 。阴影部分的面积是多少?
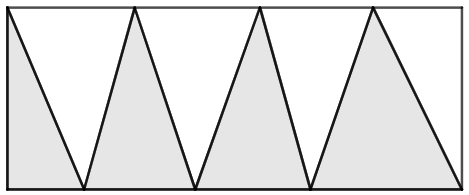
ina.c 解: 如图标注各线段长度。则长方形的面积是 \(b\cdot h\) 。阴影部分的一堆三角形的面积是: \[\dfrac{1}{2}b_1\cdot h+...+\dfrac{1}{2}b_4\cdot h=\dfrac{1}{2}\cdot(b_1+b_2+b_3+b_4)\cdot h=\dfrac{1}{2}\cdot b\cdot h\]
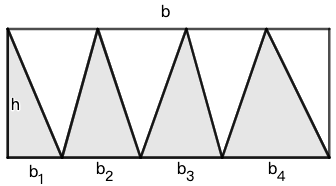
☐
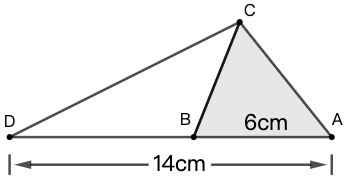
示例: 如图 7 所示,一个三角形的底边长 \(14cm\) ,剪掉 \(15cm^2\) ,即图中所示阴影部分,剩下的三角形面积有多大?
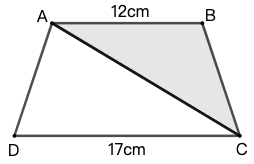
示例: 如图 8 所示,梯形的面积是 \(116cm^2\),上底是 \(12cm\) ,下底是 \(17cm\) ,求阴影部分的面积。
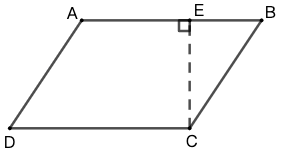
示例: 如图 9 所示,平行四边形 \(ABCD\) 的面积是 \(360cm^2\) , \(AE-12cm\) , \(CD=20cm\) , \(DE\) 垂直于 \(AB\) 。求梯形 \(ACDE\) 的面积。
三角形的等积变换
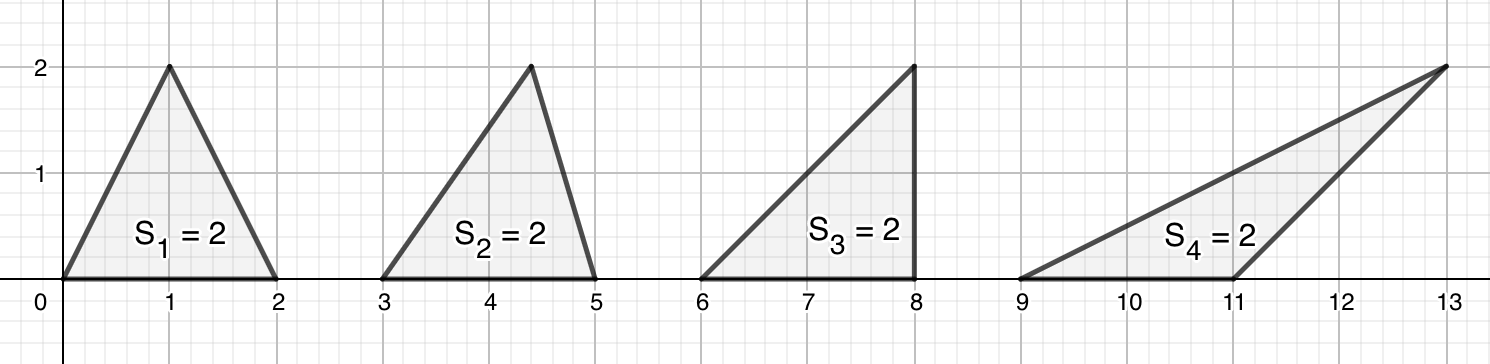
示例: 如图10所示的四个三角形具有相同的面积。
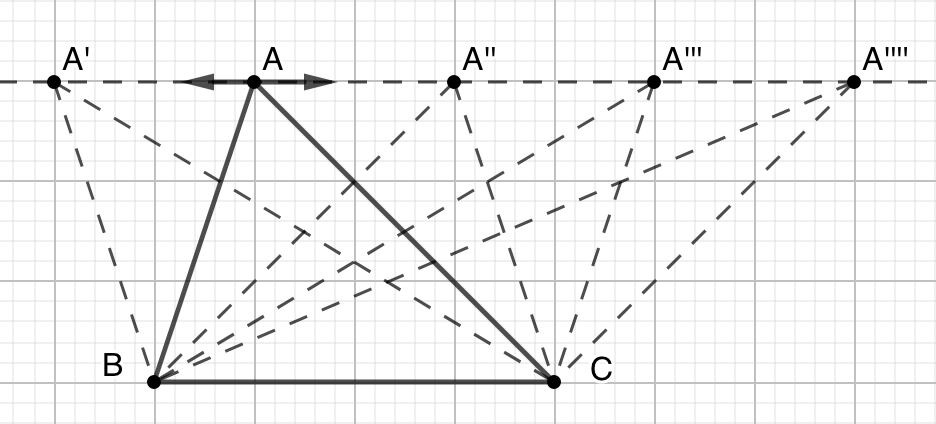
在计算三角形的面积时,任何一条边都可以作为底,所对顶点的“平移”不改变三角形的面积。在图 11 中,\(A,A',A'',...\) 所在的直线和 \(BC\) 平行。平行线间距离处处相等,所以当三角形的顶点在直线 \(AA'\) 上移动时,三角形的面积保持不变。
思考与讨论
- 你能够通过割补拼接的方法证明图10的四个三角形的面积相等么?
- 考察图10的四个三角形在等高处截水平线的长度。你能用观察到的现象说明这几个三角形面积相等么?
- 用节的Pick定理求图10中三角形的面积,是否能够得到相同的结论?
- 讨论一下,上述三种计算面积的方法,哪种可以作为三角形面积公式的。
示例: 如图12所示的四个三角形具有相同的面积。
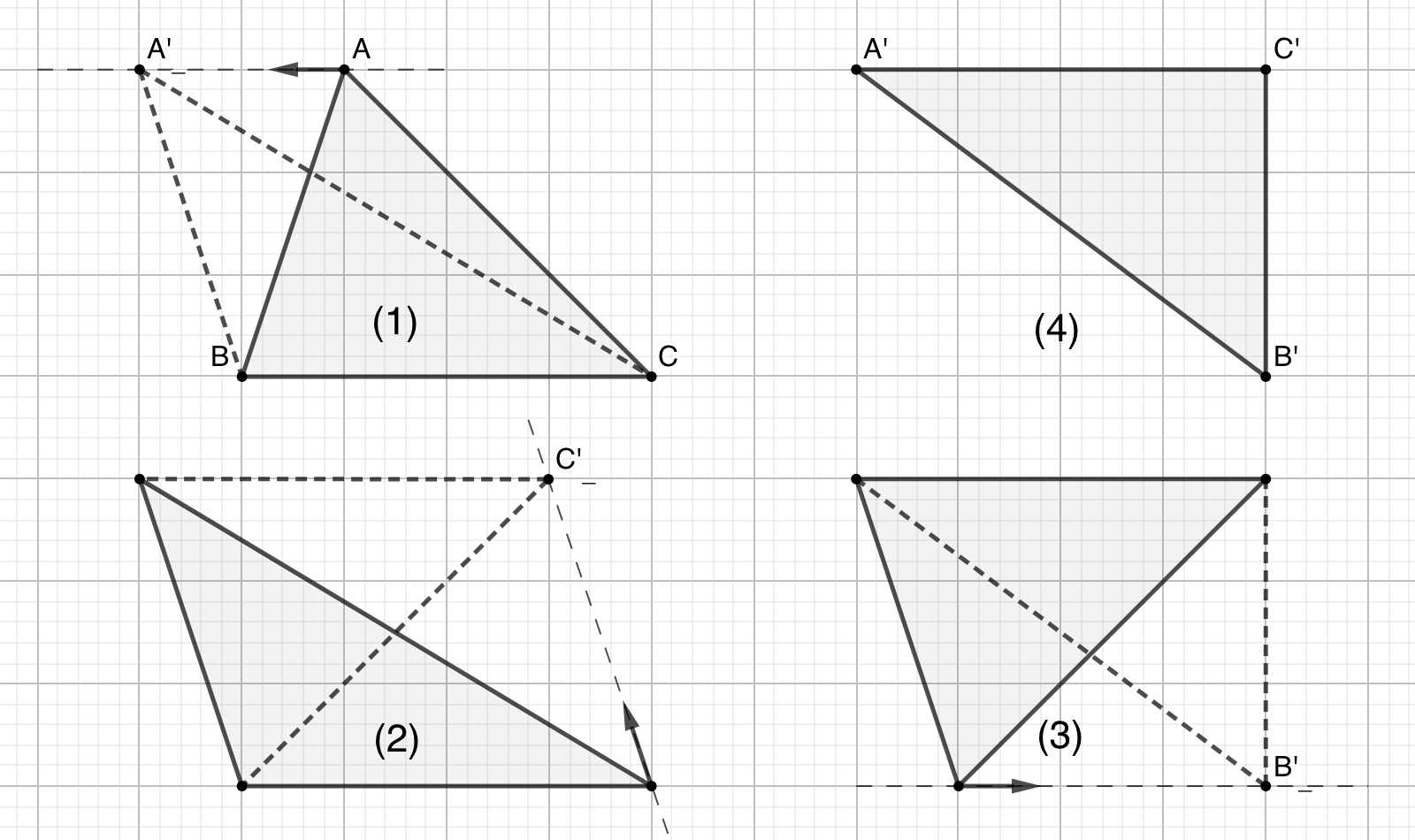
面积比转换为线段比
由三角形面积公式,上述结论是显然的。这几乎构成了小学阶段所有几何难题的解题基础(小学阶段的“难题”还有一个解题基础是勾股定理)。在小学阶段,这常用来解决初中阶段基于三角形面积公式\(S=ab\sin{\theta}\)的问题或者基于相似三角形的问题。通过一系列三角形的面积关系,绕来绕去可以得到初中阶段“直接”得出的结论
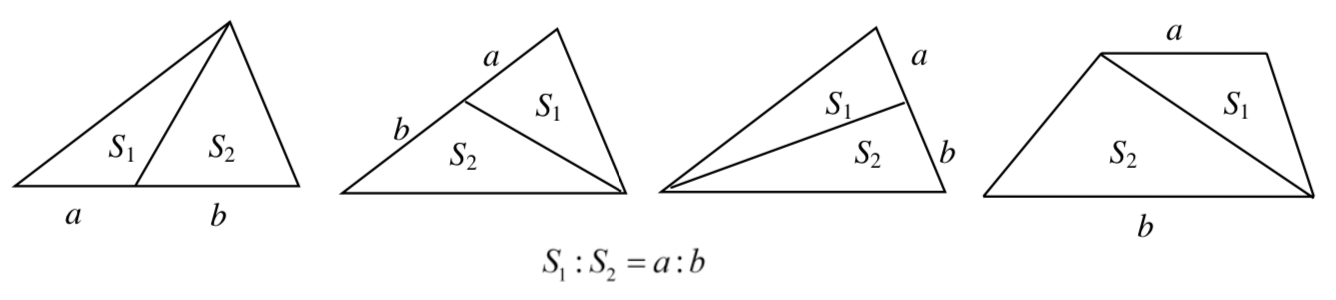
思考与讨论
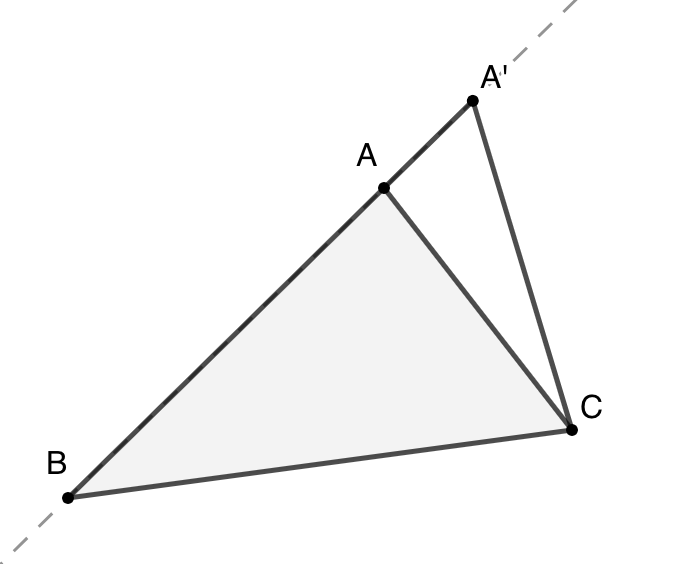
- 让三角形的某个顶点沿所在边的直线运动,如图 14 所示,三角形面积如何变化?
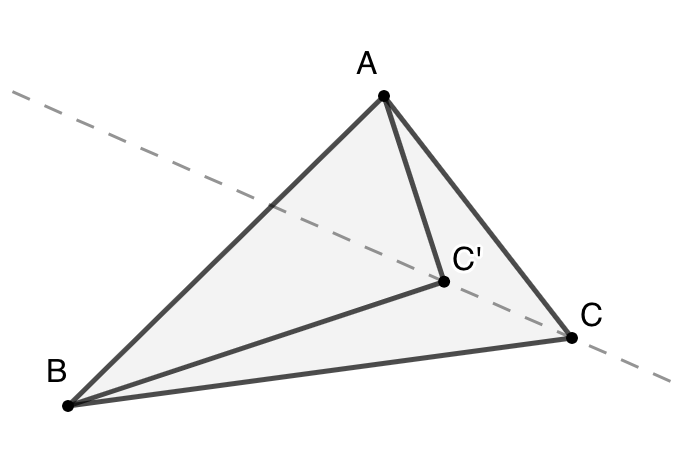
- 让三角形的某个顶点沿任意直线运动,三角形的面积如何变化?
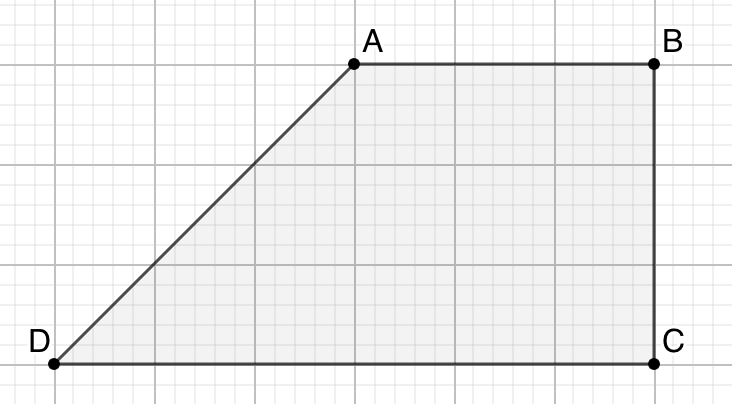
- 如何由三角形面积推导梯形(图15左)的面积公式?
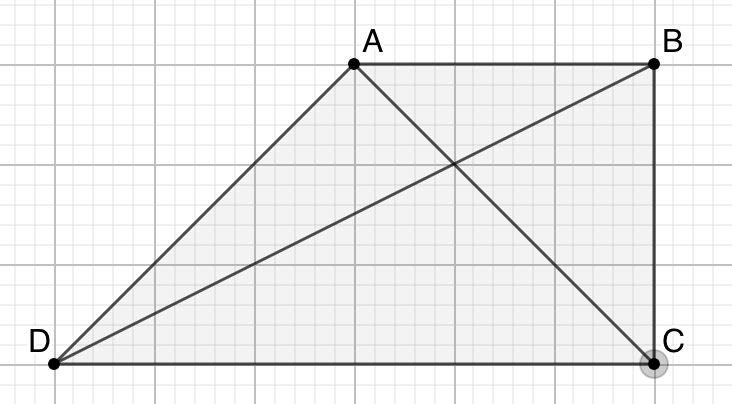
- 梯形被对角线划分后,四部分的面积关系如何(图15右)?
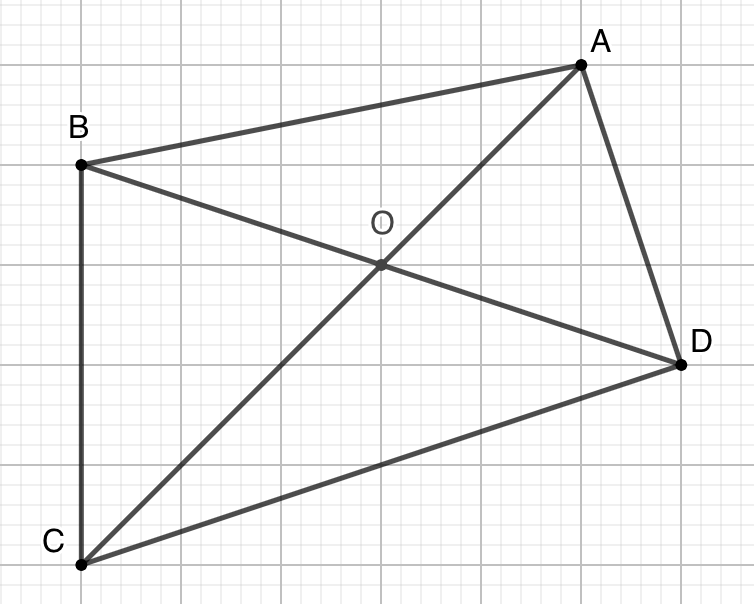
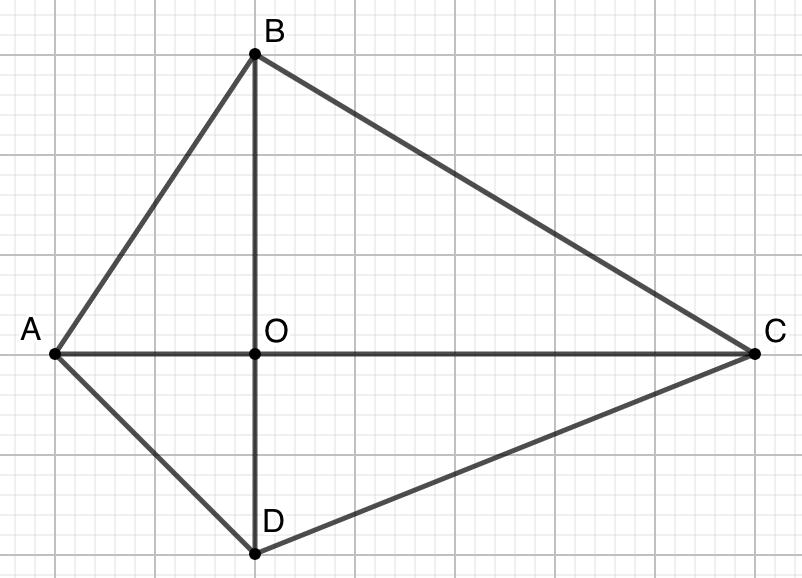
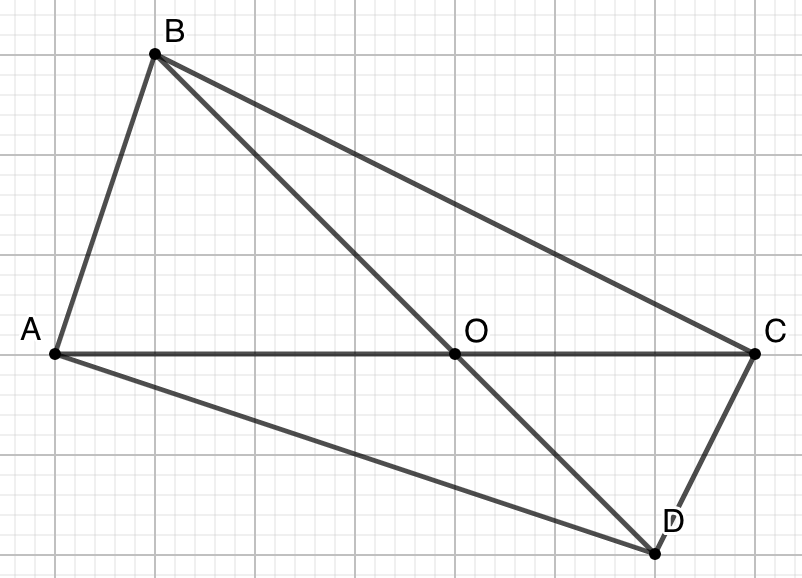
- 讨论任意四边形对角线分割的四部分的面积关系。
Pick定理(选学)
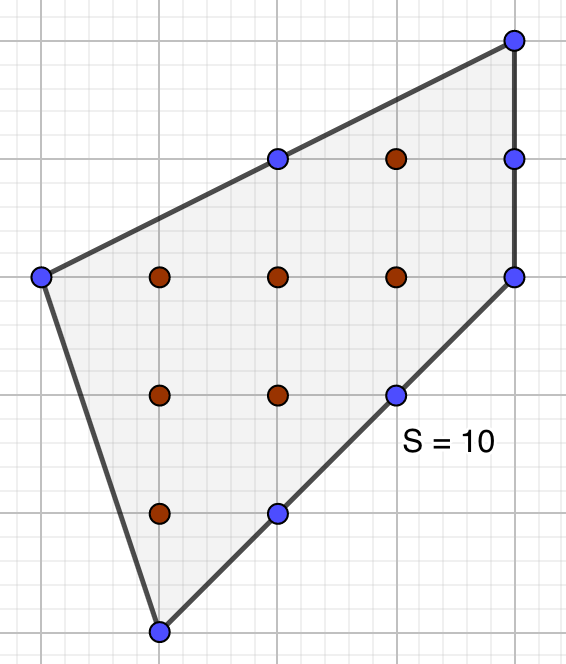
Pick定理是最简单直观的数学定理之一。其陈述如下:在正方形格点阵列中,一个小格点方块面积为1。顶点在格点上的多边形满足如下关系:\[S=a+\frac{b}{2}-1\]其中 a 表示多边形的内部节点数目,b表示边界上的格点数目,S表示多边形的面积。
示例: 以图19为例,图中多边形有 \(7\) 个内部格点,有 \(8\) 个边界格点。该多边形的面积为:\[S=7+\dfrac{8}{2}-1=10\]☐
思考与讨论
- 直接计算19的多边形面积;
- 指出在计算中使用了哪些基本原理;(应该使用尽可能少的原理。甚至三角形面积公式在本阶段也不要使用。)
- 举一些例子,验证Pick定理。应当如何设计这些例子?
- 你能想出什么思路来证明Pick定理?
- 讨论检验和证明的关系。
随堂练习
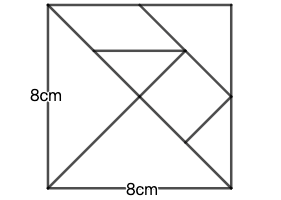
练习: 如图 20 所示,七巧板拼成的正方形边长为 \(8cm\) ,请问七巧板的各个拼板的面积是多少?
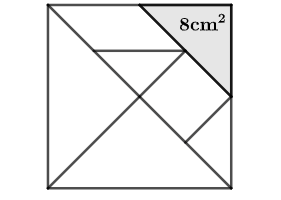
练习: 如图 21 所示,七巧板拼成的正方形中阴影的面积为 \(8cm^2\) ,请问大正方形的面积是多少?
练习: 画出图 22 中各图形(给定底上)的高。
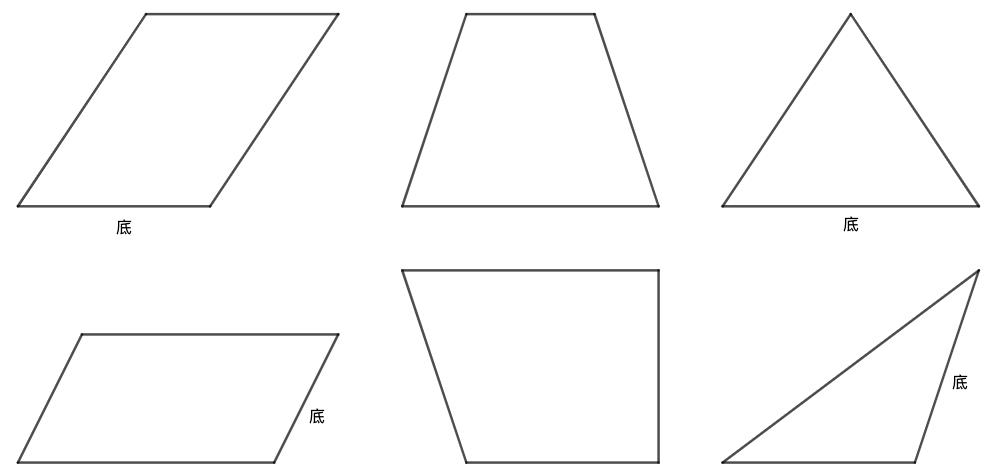
练习: 如图 23 所示, \(\triangle{ABC}\) 中 \(\triangle{ACD}\) 的面积是 \(18cm^2\) ,求阴影部分的面积。
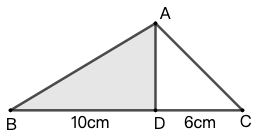
练习: 分别使用面积公式(底\(x\)高)和数格子的方法计算图 24 中图形的面积。(每个小格子的面积为 \(1\))

练习: 如图 25 所示,求平行四边形 \(ABCD\) 的周长。(单位:cm )
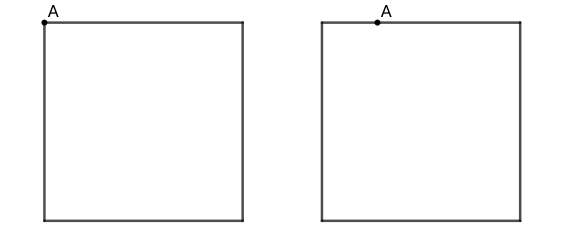
练习: 如图 26 的两个正方形中,分别做两条直线(其中一条过点 \(A\) ),将正方形分成形状和面积都相等的四部分。
练习: 将一个长方形框架(如图 27 )压扁成平行四边形,保持边长不变。压出来平行四边形有一个内角是 \(60^\circ\) 。用直尺和圆规绘制压扁后的平行四边形。
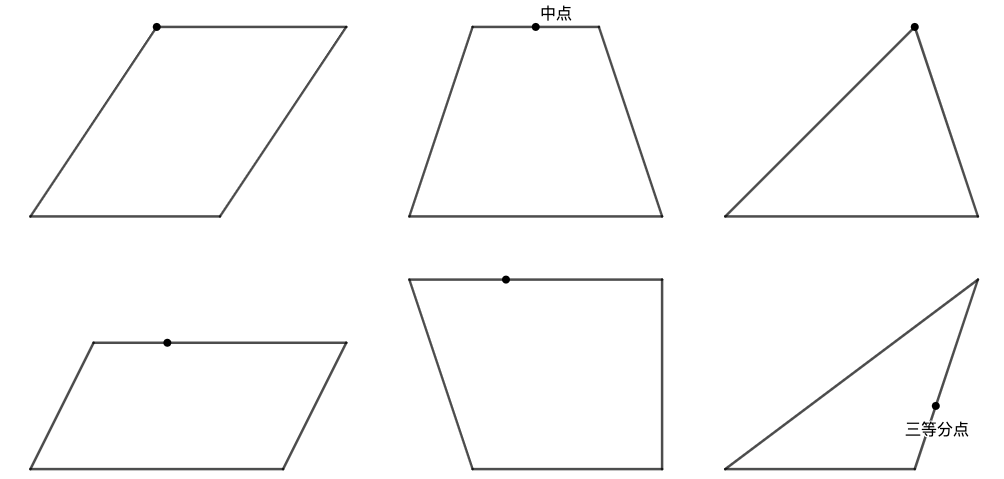
练习: 在图 28 中的各图形中,过边上给定一点做直线,平分图形面积。(注意,左下方的平行四边形和梯形边上的点位置是任取的。另外你是可以仅仅使用直尺和圆规达到题目要求的。如果图太小你无法施展圆规,可以另外画一个大图。)
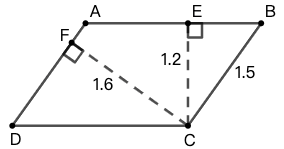
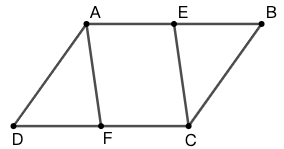
练习: 如图 29 所示,平行四边形 \(ABCD\) 的面积是 \(48cm^2\) 。 \(E\)、\(F\) 分别是上、下两边的中点,求平行四边形 \(AECF\) 的面积。(注意:这里直接告诉你 \(AECF\) 是平行四边形了,你能够根据中点条件证明 \(AECF\) 平行四边形么?)
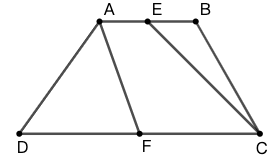
练习: 如图 30 所示,梯形 \(ABCD\) 的面积是 \(48cm^2\) 。 \(E\)、\(F\) 分别是上、下两边的中点,求四边形 \(AECF\) 的面积。
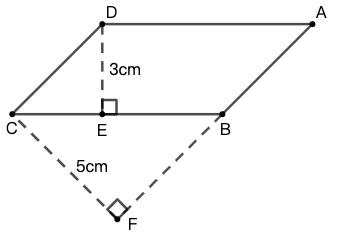
练习: 如图 31 所示,已知平行四边形 \(ABCD\) 的周长是 \(22.4cm\) 。求 \(AB\) 的长。
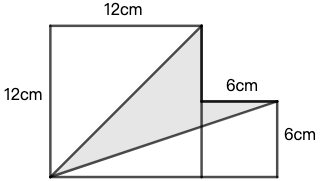
练习: 如图 32 所示,求图中阴影部分的面积。
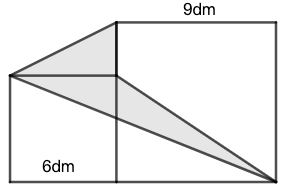
练习: 如图 33 所示,大正方形和小正方形的边长分别是 \(9dm\) 和 \(6dm\) ,求图中阴影部分的面积。
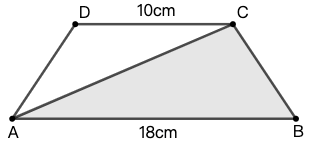
练习: 如图 34 所示,已知阴影部分的面积是 \(108cm^2\) ,求梯形 \(ABCD\) 的面积。
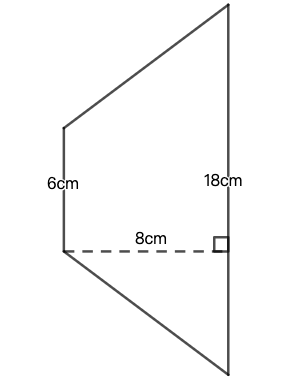
练习: 计算如图 35 所示的梯形面积。
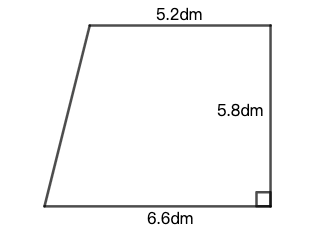
练习: 计算如图 36 所示的梯形面积。
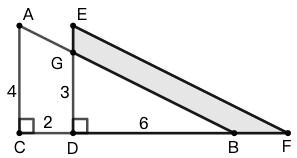
练习: 如图 37 所示,\(\triangle{ABC}\cong\triangle{EFD}\) , \(AC=4\) , \(CD=2\) , \(BD=6\) ,\(DG=3\),求阴影部分的面积。
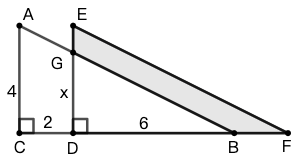
练习: 如图 38 所示,\(\triangle{ABC}\cong\triangle{EFD}\) , \(AC=4\) , \(CD=2\) , \(BD=6\) ,求线段 \(DG\) 的长度。(这道题目的设置是为了向你说明,上一道题中 \(DG=3\) 的条件是多余的)
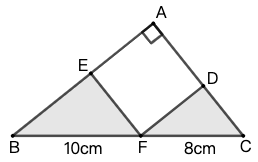
练习: 如图 39 所示, \(\triangle{ABC}\) 是直角三角形, \(BF=10cm\),\(FC=8cm\) ,\(AEFD\) 是正方形。求阴影部分的面积。
Pick定理习题
练习: 如图 40 所示, 分别使用面积公式和 Pick 定理计算各多边形的面积。

练习: 如图 41 所示, 分别使用面积公式和 Pick 定理计算各多边形的面积。
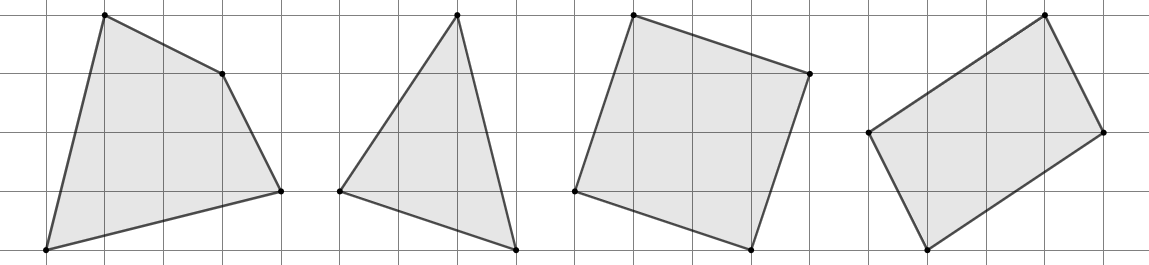
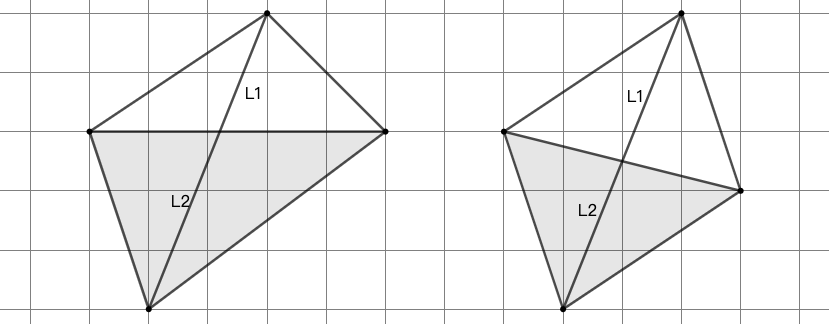
练习: 如图 42 所示, 分别使用面积公式和 Pick 定理计算各多边形的面积。
基础习题
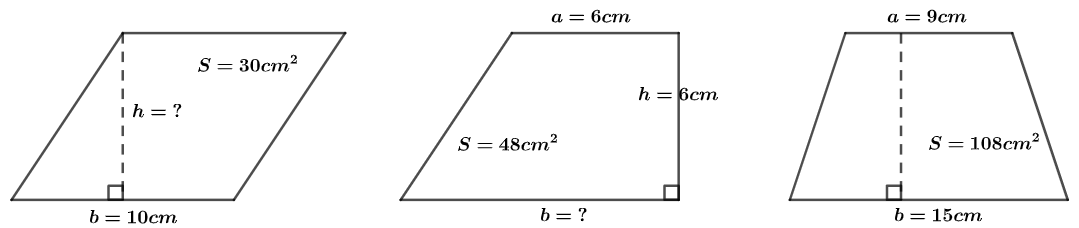
练习: 如下图所示,根据给出的条件,计算用问号标记的高或底的长度。
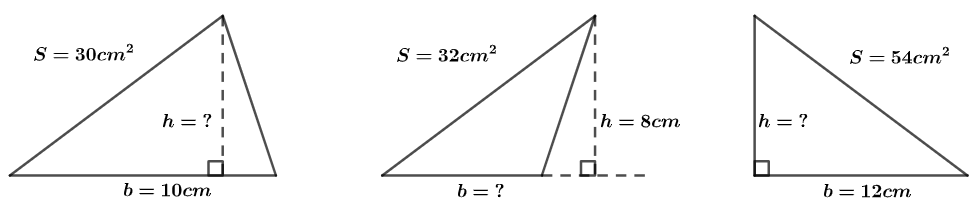
练习: 如下图所示,根据给出的条件,计算用问号标记的高或底的长度。
练习: 如下图所示,是两个相同的平行四边形。先根据左图计算平行四边形的面积,再根据右图计算所示高的长度。
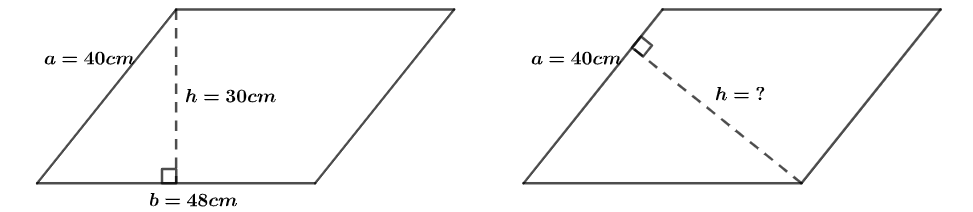
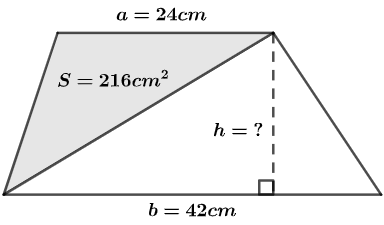
练习: 如下图所示,阴影部分三角形的面积是 \(216cm^2\) 。首先计算高 \(h\) ,再计算梯形的面积。