一元一次不等式
大小比较与证明
怎样比较大小
要比较两个数或两个代数式 \(A,B\) 的大小,可以做差 \(A-B\) ,并且考察差的符号。
比较若干个数或代数式的大小时,可将其中的字母用数值代入,看出它们的大小顺序,然后用上面的方法顺次比较每相邻两个的大小。
如果 \(A\) 和 \(B\) 是根式,并且 \(A>0,\ B>0\) ,那么只须比较 \(A^2\) 与 \(B^2\) 的大小,或者比较 \(\dfrac{A}{B}\) 与 \(1\) 的大小。
示例: 设 \(a\) 是实数,比较 \(\dfrac{1}{1+a}\) 与 \(1-a\) 的大小。
解: 做差:\(\dfrac{1}{1+a}-(1-a)=\dfrac{a^2}{1+a}\)
当 \(a=0\) 时, \(\dfrac{1}{1+a}=1-a\) ;
当 \(1+a<0\) ,即 \(a<-1\) 时, \(\dfrac{1}{1+a}<1-a\) ;
当 \(1+a<0\) ,即 $ -1<a<0$ 时, \(\dfrac{1}{1+a}>1-a\) 。☐
示例: 若 \(a,b\in\mathbb{R}\) ,比较 \(a^4+b^4\) 与 \(a^3b+ab^3\) 的大小。
解: 做差 \(D=a^4+b^4-(a^3b+ab^3)=s^4-5ps^2+5p^2\)
(其中,\(s=a+b,\ p=ab\) )
\(=(s^2-4p)(s^2-p)=(a^2-2ab+b^2)(a^2+ab+b^2)\)
\(=(a-b)^2\left[\left(a+\dfrac{b}{2}\right)^2+\dfrac{3}{4}b^2\right]\)
当 \(a\neq b\) 时 \(D>0\) , \(a^4+b^4>a^3b+ab^3\)
当 \(a=b\) 时,\(D=0\) , \(a^4+b^4=a^3b+ab^3\)☐
此题用排序不等式也可以立刻得出结论
相比等式问题,不等式问题的证明更需要解题者积极调动发散性的代数变形技巧,不等式问题的求解则需要解题者具备更加严谨的数学推导能力。在中学数学中,不等式是代数技巧的高地。反复研究各种不等式问题,可以给未来的数学之路打下坚实的基础。
在本讲义中,主要关注不等式的解。不等式的证明则将另辟主题讲解。
一元一次不等式(组)
不等式的解集
不等式的所有解组成的集合称为不等式的解集
示例: 解不等式组 \(\begin{cases} 2x+5>-3\qquad\qquad \textcircled{1}\\\dfrac{x}{3}-2>2x+1\qquad\quad\textcircled{2} \end{cases}\)
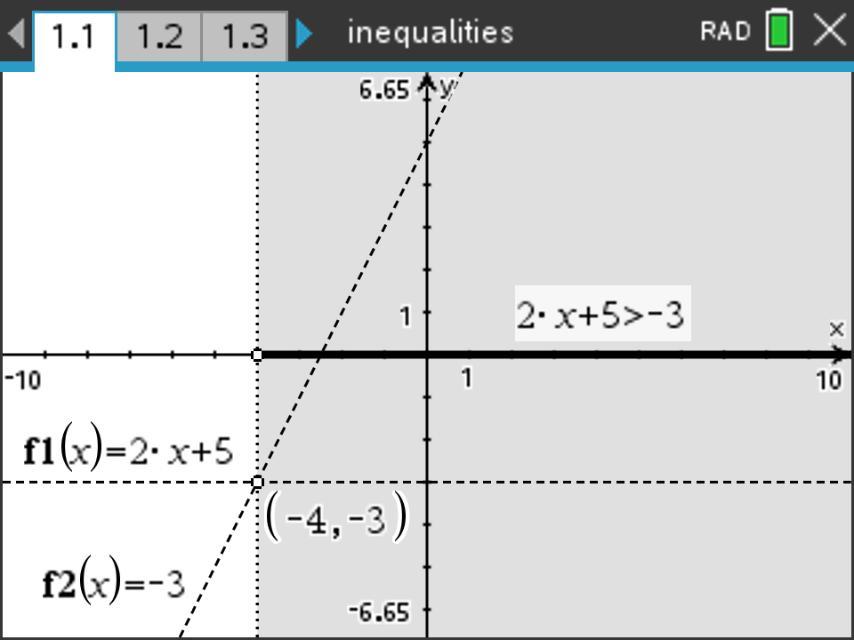
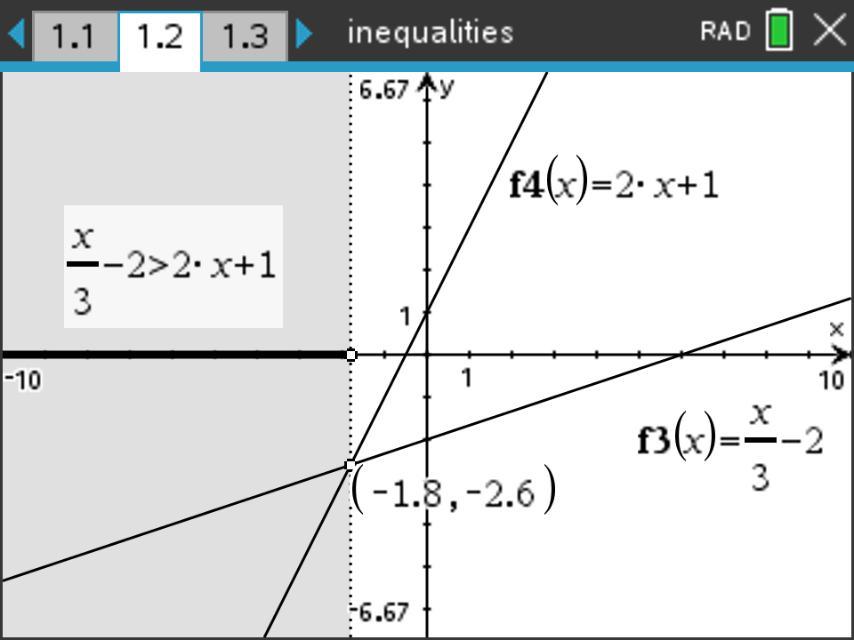

示例: 解不等式 \(\dfrac{3x+2}{18}-\dfrac{5x-4}{24}\geq\dfrac{3(2x+1)}{36}-\dfrac{x+1}{12}-\dfrac{2}{9}\)
示例: 求不等式 \(-\dfrac{1}{2}\left[(4x-3)-\dfrac{1}{3}(x+5)\right]>0\) 的正整数解。
含有字母系数的不等式
分情况讨论字母系数和常数
涉及字母系数或常数时,解不等式要注意以下事项:
\(0\) 不能做除数;
不等式两边乘(除以)负数时,不等号要改变方向。
只要在变形时时刻注意这两点,在因为字母无法确定除数和乘数时,分类讨论即可。
示例: 根据除数的符号分类讨论
解不等式 \(\dfrac{ax-2}{2}-b>x\)
解: \(\textcircled{1}\) 将不等式两边同时乘以 \(2\) ,得到: \(ax-2-2b>2x\)
\(\textcircled{2}\) 将不等式两边同时减去 \(2x-2-2b\) ,得到: \((a+2)x>2b+2\)
\(\textcircled{3}\) 将等式两边同时除以 \(a+2\) ,此时要讨论除数的三种情况:
当 \(a=-2\) 时,不等式变为 \(0>2b+2\) ,此时要进一步讨论 \(b\) :
当 \(2b+2\geq0\) 时,即 \(b\geq1\),不等式的解集为 \(\emptyset\);
等 \(2b+2<0\) 时,即 \(b<1\),不等式的解集为 \(\mathbb{R}\)
当 \(a>-2\) 时,不等式的解集为 \((\dfrac{2b+2}{a+2},\ +\infty)\)
当 \(a<-2\) 时,不等式的解集为 \((-\infty,\ \dfrac{2b+2}{a+2})\)☐
示例: 利用不等号朝向的改变反推除数符号
若不等式 \((2m-n)x+m-5n>0\) 解集为 \(x<\dfrac{10}{7}\) ,那么关于 \(x\) 的不等式 \(mx>n\ (m\neq0)\) 的解集是什么?
解: 由于解为小于号,而原不等式为大于号,因此得到:\[x<\dfrac{5n-m}{2m-n}=\dfrac{10}{7}\ ,\ 2m-n<0\bigstar\]
由于分子小于 \(0\) 所以分母也小于 \(0\) : \(5n-m<0\bigstar\bigstar\) 。
综合上述\(\bigstar\) 与 \(\bigstar\bigstar\) 得到 \(2m<n<\dfrac{m}{5}\) ,这说明 \(m,n<0\) 。
由 \(\dfrac{5n-m}{2m-n}=\dfrac{10}{7}\) 得到 \(\dfrac{n}{m}=\dfrac{3}{5}\) 。
因此 \(mx>n\) 的解集为 \((-\infty, \dfrac{3}{5})\) 。☐
示例: 解不等式 \(ax+b>cx+d\)
解: 将原不等式变形为 \((a-c)x>d-b\) 。
\(\textcircled{1}\) \(a=c\) 时, \(d\geq b\) 时,无解
\(d<b\) 时,解为全体实数
\(\textcircled{2}\) \(a>c\) 时,\(x>\dfrac{d-b}{a-c}\)
\(\textcircled{2}\) \(a<c\) 时,\(x<\dfrac{d-b}{a-c}\)☐
示例: 解不等式 \(a^2x-1>a(x-1)\)
示例: 设不等式 \((a+b)x+(2a-3b)<0\) 的解是 \(x<-\dfrac{1}{3}\) ,求不等式 \((a-3b)x+(b-2a)>0\) 的解。
使用图像法求解不等式
示例: 使用图像法求解不等式
求使不等式 \(2x-1>m(x-2)\) 对 \(0<m<3\) 的一切 \(m\) 都成立的 \(x\) 。
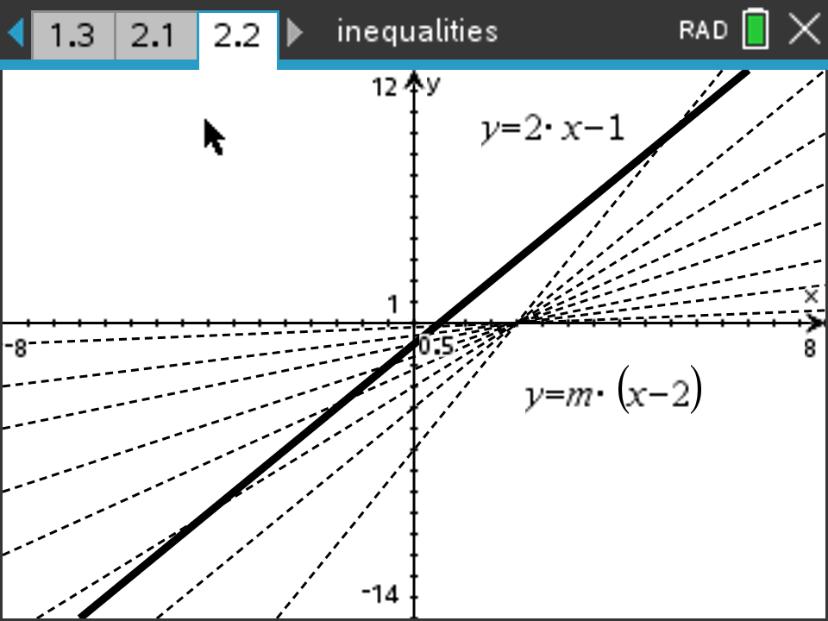

解: 将不等式的两侧看作两条直线的方程: \[\begin{align*} y&=2x-1 &\textcircled{1}\\ y&=m(x-2) &\textcircled{2} \end{align*}\]
在上两式中,只要求出对 \(0<m<3\) 内的一切 \(m\) 值,使 \(\textcircled{1}\) 位于 \(\textcircled{2}\) 上方的横坐标范围即可。如图 4 所示,所求的横坐标范围即为 \(m=0\) 与 \(m=3\) 时两次交点的横坐标限定的区间。
☐
示例: 使用图像法求解不等式
求使不等式 \(x-3>kx+2\) 对 \(-1\leq k\leq4\) 的一切 \(k\) 都成立的 \(x\) 。
含有绝对值的不等式
绝对值的处理方法
不等式含有绝对值时,通常的处理方法是分绝对值内部算式的符号情况去掉绝对值符号。另外,绝对值符号在数轴上的几何意义有时候也可以帮助求解一些简单的问题。
示例: 解不等式 \(|x+2|>3\)
解法一 依据去绝对值后的符号,分情况讨论:
\(\textcircled{1}\) \(x+2>0\) ,即 \(x\in(-2,+\infty)\) 时,不等式变为 \(x+2>3\)
解得:\(x\in(1,+\infty)\)
\(\textcircled{2}\) \(x+2\leq0\) ,即 \(x\in(-\infty,-2]\) 时,不等式变为 \(-(x+2)>3\)
解得:\(x\in(-\infty,-5)\)
综上所述,不等式的解集为 \((-\infty,-5)\cup(1,+\infty)\) 。☐
解法二 结合绝对值符号的几何意义:
\(|x+2|\) 代表 \(x\) 到 \(-2\) 在数轴上的距离。
\(|x+2|>3\) 代表 \(x\) 到 \(-2\) 在数轴上的距离大于 \(3\) 的点的集合。
如图 6 所示,就是不等式的解集。

☐
示例: 解不等式 \(|x+2|+|x-3|>7\)
示例: 平方去绝对值
解不等式 \(|x+1|>|2x-3|\)
解: 原不等式等价于 \((x+1)^2>(2x-3)^2\)
整理得 \(3x^2-14x+8<0\) 即 \((x-4)(3x-2)<0\)
因此 \(\dfrac{2}{3}<x<4\) 。☐
思考与讨论
- 使用分区间讨论的方法如何求解上述不等式?
- 使用图像法如何求解上述不等式?

♣ 遇到单侧绝对值的不等式使用平方去绝对值时,要特别注意进行等价变换的细节。请使用平方去绝对值讨论如下两个题目:
示例:1 平方去绝对值
解不等式 \(|x+1|<2-3x\)
示例: 平方去绝对值
解不等式 \(|x+1|>2-3x\)
♣ 遇到单侧绝对值的不等式时,使用图像法也是一个不错的方法。请看如下示例:
示例:2 图像法处理单侧绝对值不等式
解不等式 \(|x+2|>\dfrac{3x+14}{5}\)

习题:解不等式基础练习
练习:3 解不等式 \(2-\dfrac{1}{2}x>\dfrac{x-12}{3}\)
练习:4 解不等式 \(\dfrac{2x+1}{3}\leq\dfrac{2x-1}{2}\)
练习:5 解不等式 \(\dfrac{2x-1}{3}>1-\dfrac{4x+3}{2}\)
练习:6 解不等式 \(|2-x|<1\)
练习: 解不等式 \(|2x-4|<5\)
练习: 解不等式 \(|3-2x|>4\)
练习:7 解不等式 \(\left|\dfrac{x-1}{2}\right|<5\)
练习:8 利用图像法解不等式
(1) \(2x-3>x+2\) (2) \(|x-1|<3\)
练习:9 解不等式 \(|x-3|<|2x-1|\)
练习:10 解不等式 \(\dfrac{1}{4}<\left|\dfrac{x}{2}-1\right|<\dfrac{1}{2}\)
练习:11 解不等式 \(3|x-2|\leq10-x\)
习题:含有字母的不等式
练习:12 解不等式 \(ax+2>x+b\)
练习: 若不等式 \((2a-b)x+3a-4b<0\) 的解为 \(x>\dfrac{4}{9}\) 。则不等式 \((a-4b)x+2a-3b>0\) 的解集是什么?
练习: 解不等式组 \(\begin{cases}3mx-1<10-mx\\mx+x>(1-2m)x+8\end{cases}\)
习题:不等式综合问题
练习: 若不等式 \(|x+1|-|x-2|>k\) 恒成立,则实数 \(k\) 的取值范围是什么?
练习:13 求同时满足 \(a+b+c=6,\ 2a-b+c=3,\ b\geq c\geq0\) 的 \(a\) 的最大值及最小值。
练习:14 \(\bigstar\bigstar\) 若对 \(x\geq-1\) , \(y\leq3\) , 一次式 \(ax+by+2\) 恒为正,求 \((a,b)\) 的范围,并用图像表示。