旋转相似

相似形通论

图形的基本变换

平移，即平行移动，图形中的每一个点依同一个方向移动同样的距离；
旋转，图形中的每一个点绕一定点旋转同样的角度；
放缩，关于一个固定的位似中心放缩；
反射，将直线以某条直线为对称轴翻转；

将一个图形施行任意多次上述变换，最后所得图形与原来的图形相似，并且根据反射的次数为偶数或奇数，相似为顺相似或逆相似。两者的相似比，等于其中各次放缩的比的乘积。

转缩和相似中心

定义：用“转缩”一词表示关于一个点的旋转及随后的关于同一点的放缩。（做为特殊情况，仅有旋转或仅有放缩，也称为转缩。）

定理：任一条线段 \(AB\) ，可以用一次平移或转缩变换，与任意一条线段 \(A'B'\) 重合。

定理：如果两个图形顺相似，并且一个图形有两个点与另一个图形的两个对应点相重合，那么这两个图形处处重合。

定理：如果两个图形全等，那么必有一个旋转或平移，使得二者重合。如果两个图形顺相似，那么必有一个转缩，使二者重合。

定义：转缩或旋转的中心称为这两个图形的相似中心；旋转角与放缩的比分别称为相似角与相似比。

定理：通过一对对应点及过它们的对应直线的交点的圆也通过相似中心。

示例：如果 \(AB\parallel A'B'\) ，找出上述定理所需的变换。（注意需要分 \(\overrightarrow{AB}\) 与 \(\overrightarrow{A'B'}\) 同向或者反向两种情况。）

示例：如果 \(AB\) 与 \(A'B'\) 所在直线相交于 \(P\) ，并且这四点均不与 \(P\) 重合。证明图 1 所示图形中，

（1）证明 \(\triangle{OAB}\sim\triangle{OA'B'}\)。

（2）如果点 \(B\) 与点 \(P\) 重合，图形如何？是否有类似结论？

寻找两条线段的旋转变换中心

示例：在平面直角坐标系中，点 \(A(0,1)\) 在 \(y\) 轴上，点 \(B\) 的坐标为 \((3,2)\) ，在 \(x\) 轴上面确定一点 \(P\) 使得 \(\dfrac{1}{2}AP+BP\) 的值最小。（提示：作 \(Rt\triangle{APC}\) 使得 \(AP=2PC\) ，考察 \(C\) 点轨迹和 \(PC+BP\) ）

由相似得到轨迹

示例：如图 3 所示， \(O\) 是正三角形 \(ABC\) 边 \(AC\) 的中点，也是正三角形 \(DEF\) 边 \(DF\) 的中点，求证 \(AD\perp BE\) 并求 \(\dfrac{AD}{BE}\) 。

分析 \(\triangle{ABC}\) 绕着 \(O\) 进行转缩变换，变换后的三角形为 \(\triangle{DEF}\) ，其中点 \(A\) 的轨迹为 \(AD\) ，点 \(B\) 的轨迹为 \(BC\) 。由旋转相似的理论可知 \(\dfrac{AD}{BE}=\dfrac{AO}{BO}=\dfrac{1}{2}\) 且由于 \(\angle{AOB}=90^\circ\) 有 \(AD\perp BE\) 。

从证明的角度，只需将轨迹的端点与旋转中心连线，证明连出的三角形相似即可。即证明 \(\triangle{AOD}\sim\triangle{BOE}\) 。至于垂直关系，通过一顿眼花缭乱的倒角（或四点共圆）即可证明。请读者自行补充证明。

将轨迹端点与旋转中心连线，会得到一组相似三角形 \(\triangle{AOD}\sim\triangle{BOE}\)

旋转相似解题套路

找到旋转变换的点轨迹（\(AD,BE\)），轨迹的相似比为点到旋转中心的距离之比（\(AD:BE=AO:BO\)），利用轨迹线段对旋转中心张成的相似三角形可证（\(\triangle{AOD}\sim\triangle{BOE}\)）。
轨迹的夹角等于点到旋转中心的连线夹角（ \(AD,BE\) 所成角等于 \(\angle{AOB}\)），利用两条轨迹线段的起点和交点还有旋转中心四点共圆可证（\(AOBG\) 或 \(DOEG\)），证明时要用到相似形得到的等角关系。

示例：如图 5 所示，以平面上一点 \(O\) 为直角顶点，分别画出两个直角三角形，记作 \(\triangle{AOB}\) 和 \(\triangle{COD}\)，其中 \(\angle{ABO} =\triangle{DCO}=30^\circ\) 。点 \(E\)、\(F\)、\(M\) 分别是 \(AC\)、\(CD\)、\(DB\) 的中点，连接 \(FM\)、\(EM\)。求 \(\dfrac{FM}{EM}\) 的值.

分析本题可以看作 \(\triangle{OAB}\) 旋转至 \(\triangle{ODC}\) 。虽然最终要处理的两条线段不直接是轨迹，但可以和轨迹建立关联： \(MF\) 平行且等于 \(\dfrac{1}{2}BC\) ， \(EF\) 平行且等于 \(\dfrac{1}{2}AD\) 。

至于证明方法，依然是证明轨迹到旋转中心张成的三角形相似，即 \(\triangle{OAD}\sim\triangle{OBC}\) ，如图 6 所示。请读者自行补充完整证明。

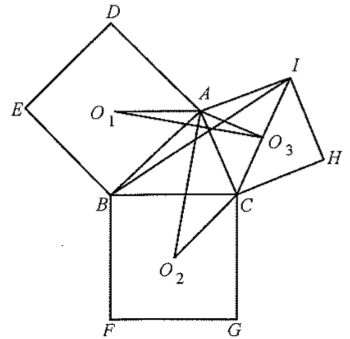
示例：如图 7 所示，分别以 \(\triangle{ABC}\) 的三边向外做正方形， \(O_1,O_2,O_3\) 是三个正方形的中心。求证： \(AO_2\) 与 \(O_1O_2\) 垂直且相等。

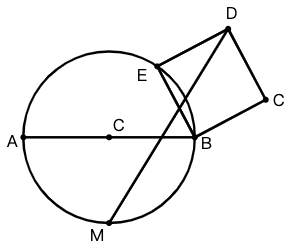
示例：已知 \(\odot O\) 的半径为 \(6\) ， \(E\) 是 \(\odot O\) 上一个动点，以 \(BE\) 为边按顺时针方向作正方形 \(BEDC\) ，\(M\) 是弧 \(AB\) 的中点，当 \(E\) 在圆上移动时， \(MD\) 的最小值是多少？（填空题）

北大附中数竞初二平时测验

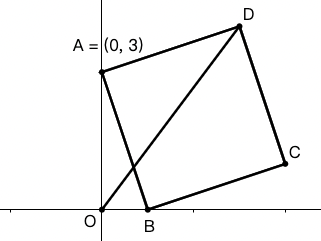
示例：在平面直角坐标系 \(xOy\) 中，已知点 \(A(0,3)\) ，点 \(B\) 为 \(x\) 轴上一个动点，以 \(AB\) 为边在 \(AB\) 右侧作正方形 \(ABCD\) ，连接 \(OD\) ，求线段 \(OD\) 长度的最小值。

清华附中数竞初二期中测验（创新班）

由轨迹得到相似

在上一节我们讨论了图形进行相似旋转后对应点轨迹的关系。本节我们反过来讨论这类问题，即在获得关于轨迹信息的前提下，寻求相似图形的证明过程。

示例：如图 10 所示，已知 \(\triangle{ABC}\) ，\(PB\) 和 \(PC\) 是两条运动路径，满足 \(\angle{BPC}=\angle{BAC}\) 。 \(B,C\) 沿着 \(PB, PC\) 同方向运动至 \(B',C'\) ，运动过程中以下满足四个条件之一：

xxx

\(\angle{A}\) 保持不变；
\(\angle{B}\) 保持不变；
\(\angle{C}\) 保持不变；
\(BB':CC'=BA:CA\) 。

求证：运动过程中，\(\triangle{ABC}\) 形状不变，即 \(\triangle{ABC}\sim\triangle{AB'C'}\) 。

示例：在 \(\triangle{ABC}\) 中，\(\angle{A}=90^\circ, AB=AC\) ，点 \(D\) 为 \(BC\) 的中点。

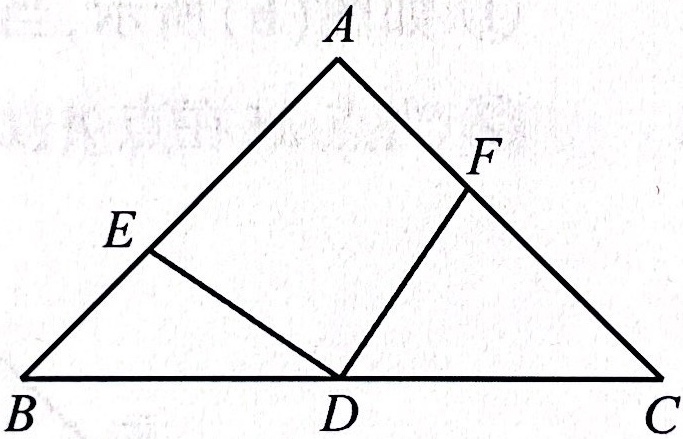
[(1)] 如图所示，若点 \(E,F\) 分别为 \(AB,AC\) 上的点，且 \(DE\perp DF\) ，求证： \(BE=AF\) ；
[(2)] 若点 \(E,F\) 分别为 \(AB,CA\) 延长线上的点，且 \(DE\perp DF\) ，求证： \(BE=AF\) 。

示例：如图所示，在 \(\triangle{ABC}\) 中， \(\angle{ACB}=90^\circ\) ，\(CD\) 是中线， \(AC=BC\) 。一个以点 \(D\) 为顶点的 \(45^\circ\) 角绕点 \(D\) 旋转，使角的两边分别与 \(AC,BC\) 的延长线相交，焦点分别为 \(E,F\) 。\(DF\) 与 \(AC\) 交于点 \(M\) ，\(DE\) 与 \(BC\) 交于点 \(N\) 。

2017 湖北襄阳.第24题

[(1)] 如图 (a) 所示，若 \(CE=CF\) ，求证：\(DE=DF\)；
[(2)] 如图 (b) 所示，探究线段 \(AB,CE,CF\) 之间的数量关系；
[(3)] 若 \(CE=4,CF=2\) ，求 \(DN\) 的长。

直线旋转构造角度

示例：在等腰直角三角形 \(ABC\) 中，\(\angle{ACB}=90^\circ\) ， \(P\) 是线段 \(BC\) 上一动点（不与点 \(B,C\) 重合），连接 \(AP\) ，延长 \(BC\) 至点 \(Q\) ，使得 \(CQ=CP\) ；过点 \(Q\) 作 \(QH\perp AP\) 于点 \(H\) ，交 \(AB\) 于点 \(M\) 。

2017 北京.第28题

[(1)] 若 \(\angle{PAC}=\alpha\) ，求 \(\angle{AMQ}\) 的大小（用含 \(\alpha\) 的式子表示）；
[(2)] 用等式表示线段 \(MB\) 与 \(PQ\) 之间的数量关系，并给予证明。

示例：如图所示，在等腰三角形 \(ABC\) 中， \(\angle{BAC}=120^\circ\) ，\(AB=AC=2\) ，点 \(D\) 是 \(BC\) 边上的一个动点（不与 \(B,C\) 重合），在 \(AC\) 上取一点 \(E\) ，使 \(\angle{ADE}=30^\circ\) 。

2017 山东东营.第24题

[(1)] 求证：\(\triangle{ABD}\sim\triangle{DCE}\)；
[(2)] 设 \(BD=x, AE=y\) ，求 \(y\) 关于 \(x\) 的函数关系式并写出自变量 \(x\) 的取值范围；
[(3)] 当 \(\triangle{ADE}\) 是等腰三角形时，求 \(AE\) 的长。

番外：硬凑条件的题目

示例：

2018 四川眉山.第25题

习题

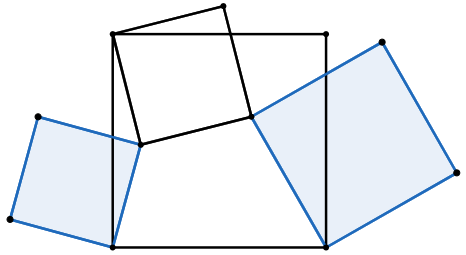
练习：有如图所示的四个正方形，求两个阴影正方形面积之比。

练习：如图所示，在 \(\triangle{ABC}\) 中， \(\angle{BAC}=90^\circ, AB=AC, AD\perp BC\) 于点 \(D\) 。点 \(M,N\) 分别在直线 \(AD,AC\) 上，且 \(\angle{BMN}=90^\circ\) 。

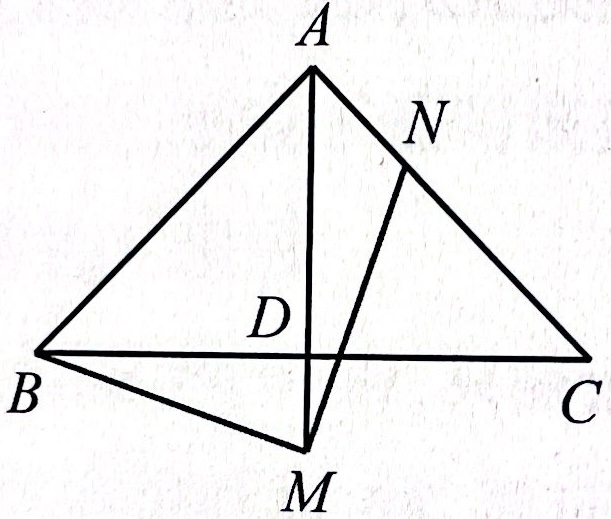
[(1)] 如图所示，当点 \(M\) 在 \(AD\) 的延长线上时，求证：\(AB+AN=\sqrt{2}AM\) ；
[(2)] 当点 \(M\) 在点 \(A,D\) 之间，且 \(\angle{AMN}=30^\circ\) 时，已知 \(AB=2\) ，求线段 \(AM\) 的长。

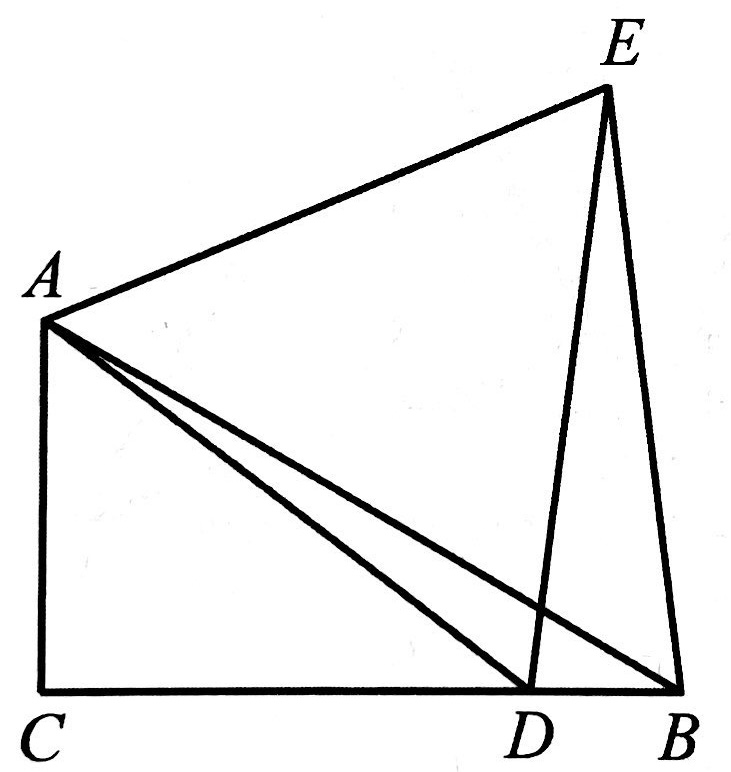
练习：如图所示，在 \(Rt\angle{ABC}\) 中， \(\angle{ACB}=90^\circ\) ， \(\angle{ABC}=30^\circ\) ，则 \(AC=\dfrac{1}{2}AB\) 。点 \(D\) 是直线 \(CB\) 上任意一点，连接 \(AD\) ，作等边 \(\triangle{ADE}\) ，连接 \(BE\) 。探究线段 \(BE\) 与 \(DE\) 之间的数量关系。

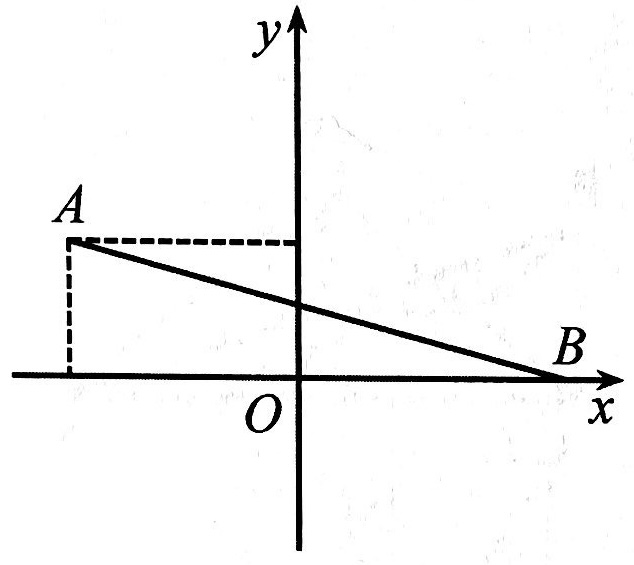
练习：如图所示，在平面直角坐标系 \(xOy\) 中，点 \(A\) 的坐标为 \((-\sqrt{3},1)\) ，点 \(B\) 是 \(x\) 轴正半轴上的一动点，以 \(AB\) 为边作等边 \(\triangle{ABC}\) 。当点 \(C\) 在第一象限内且点 \(B\) 的坐标是 \((2,0)\) 时，求点 \(C\) 的坐标。

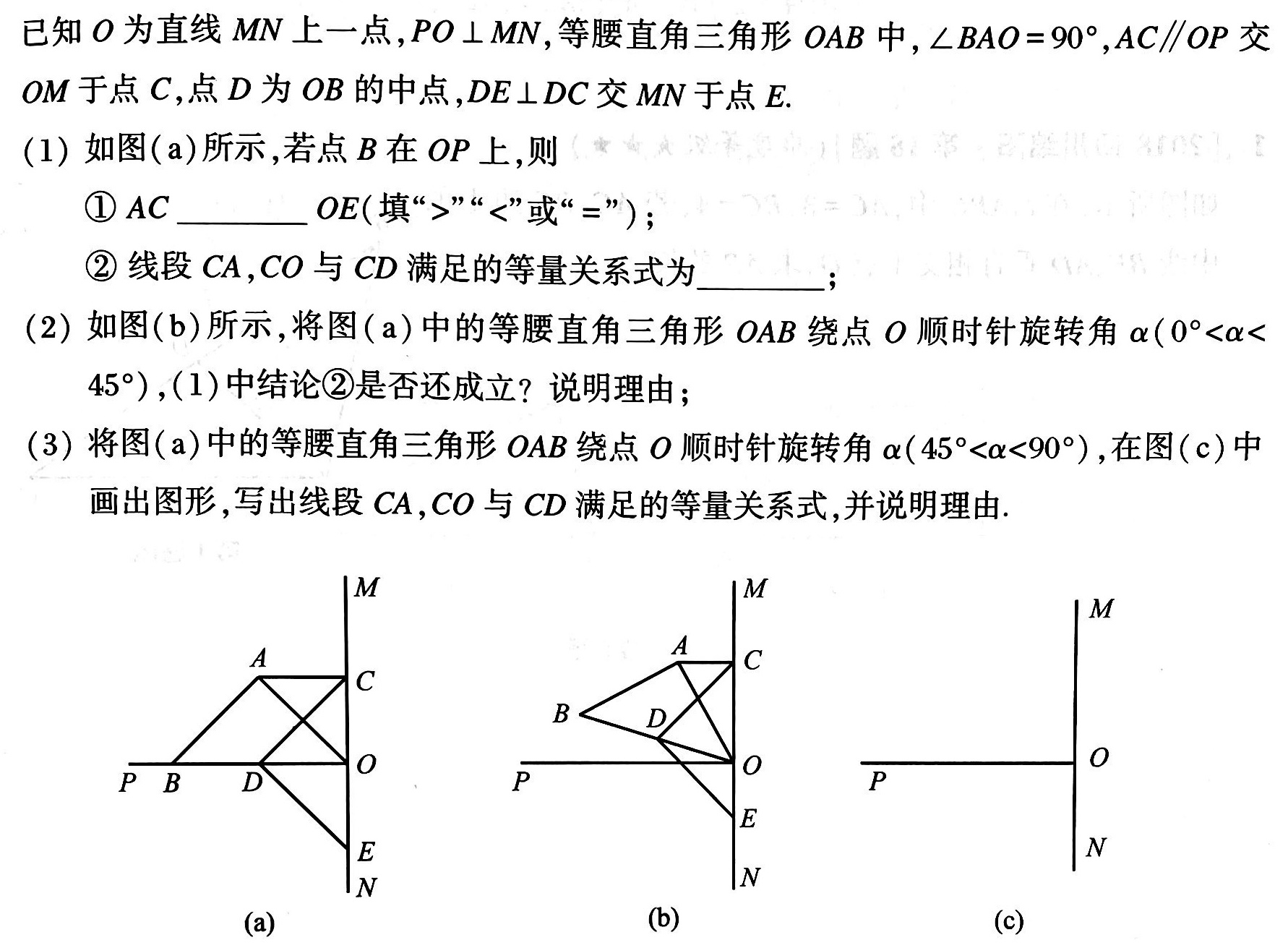
练习：

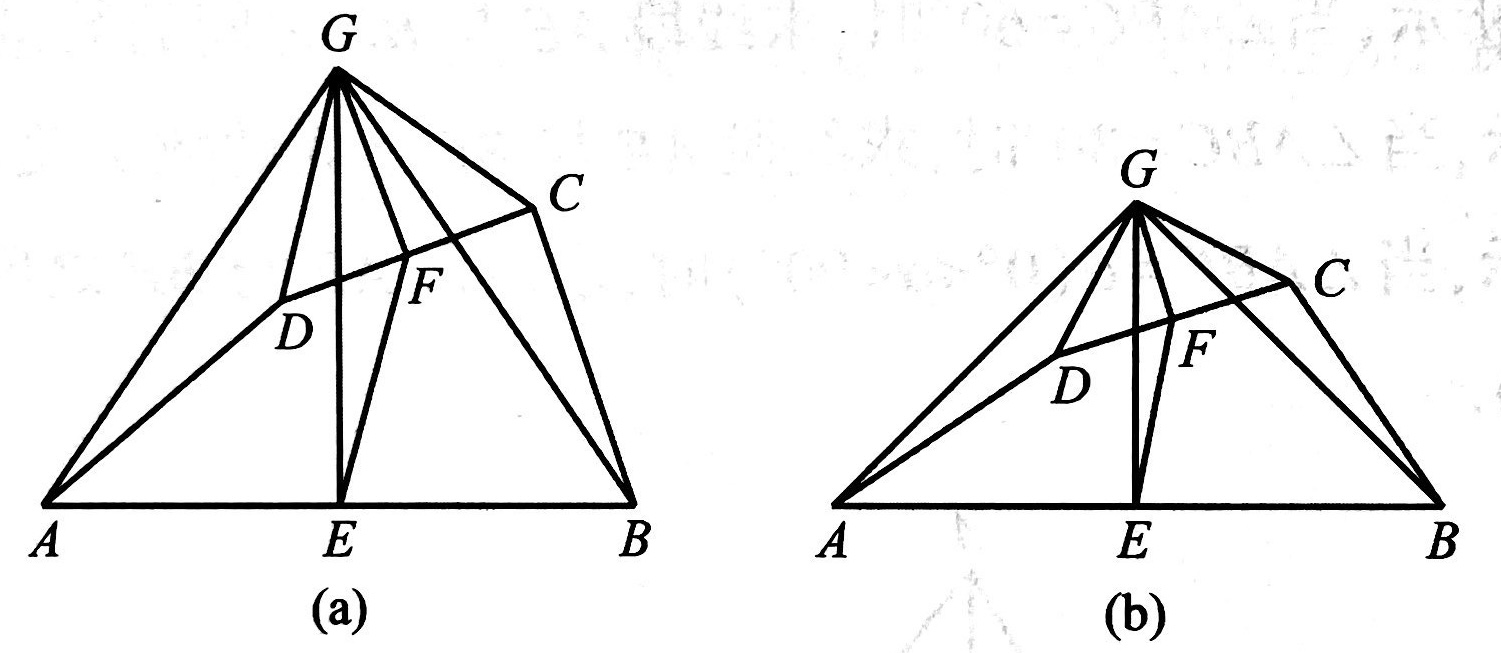
练习：如图所示，在四边形 \(ABCD\) 中，点 \(E,F\) 分别是 \(AB,CD\) 的中点，过点 \(E\) 作 \(AB\) 的垂线，过点 \(F\) 作 \(CD\) 的垂线，两垂线交于点 \(G\) ，连接 \(GA,GB,GC,GD,EF\) ，若 \(\angle{AGD}=\angle{BGC}\) 。

[(1)] 求证： \(AD=BC\) ；
[(2)] 求证： \(\triangle{AGD}\sim\triangle{EGF}\) 。

2015 安徽.第23题

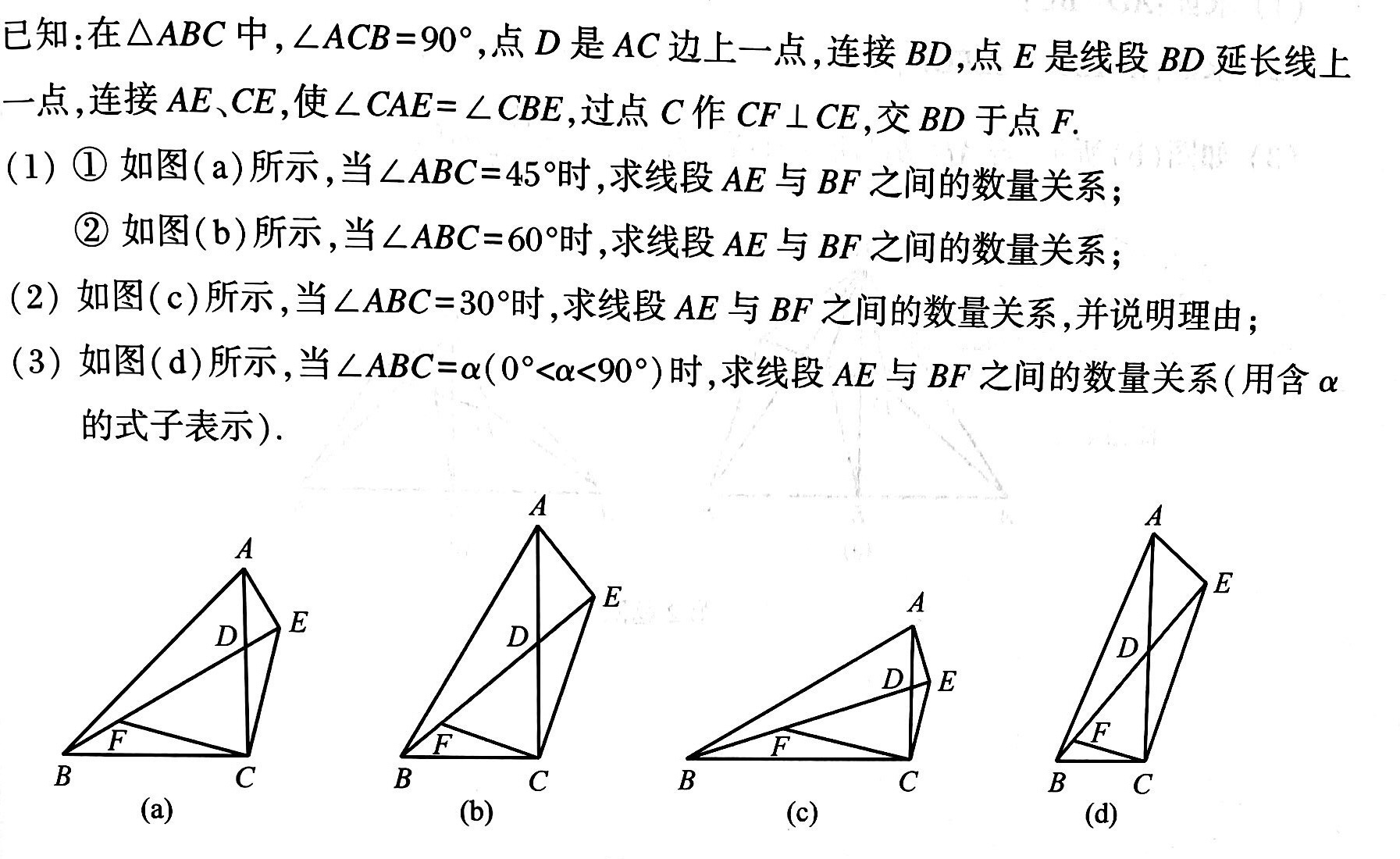
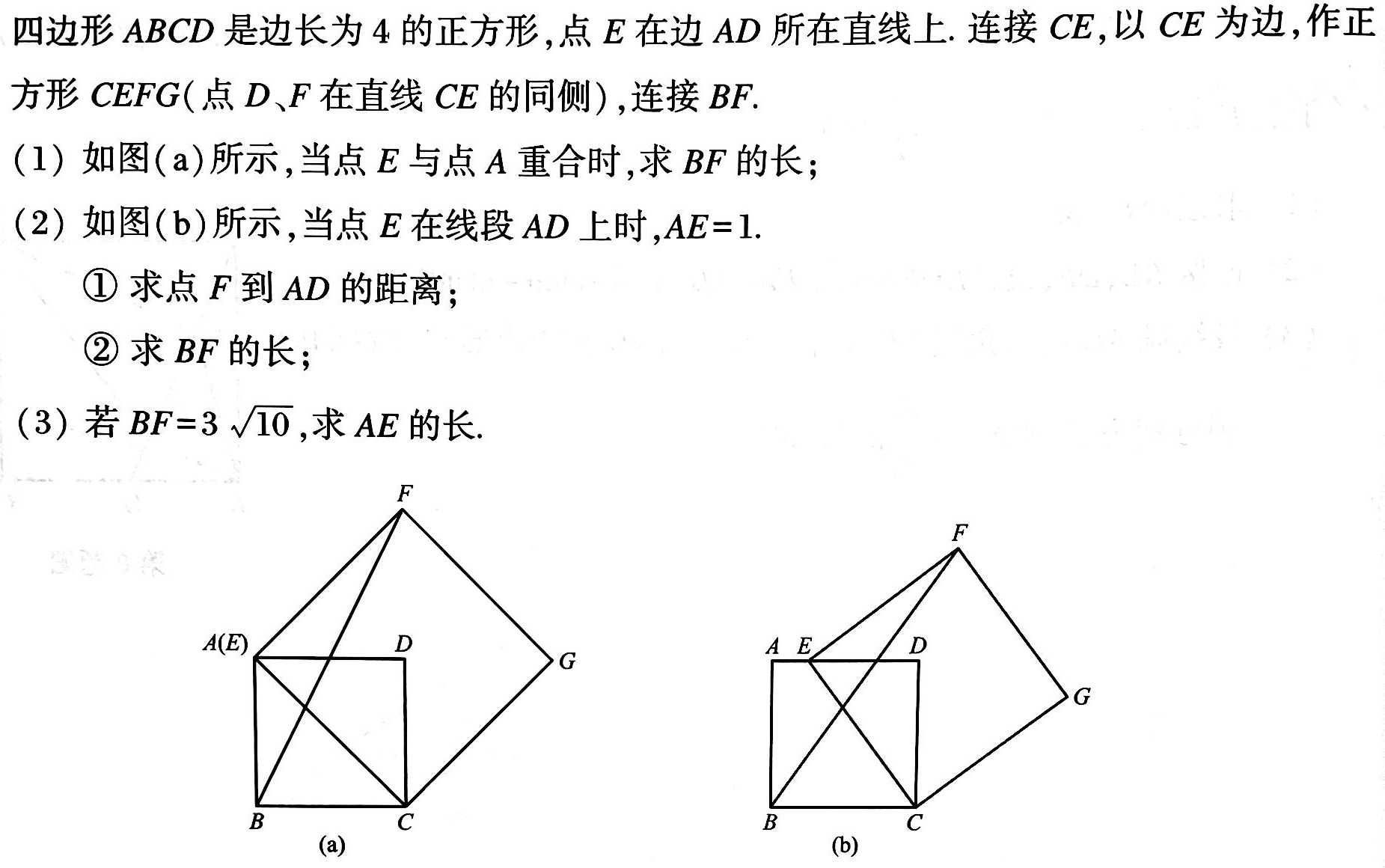
练习：