二元一次不等式组
直线方程的正方向
直线方程的“正方向”
直线 \(Ax+By+C=0\) 将直角坐标系平面分为两个区域。
法向量 \(\begin{bmatrix} A\\B \end{bmatrix}\) 指向“正区域”,即 \(Ax+Bx+C>0\) 的区域。
平面的另一半是“负区域”,即满足 \(Ax+Bx+C<0\) 的区域。
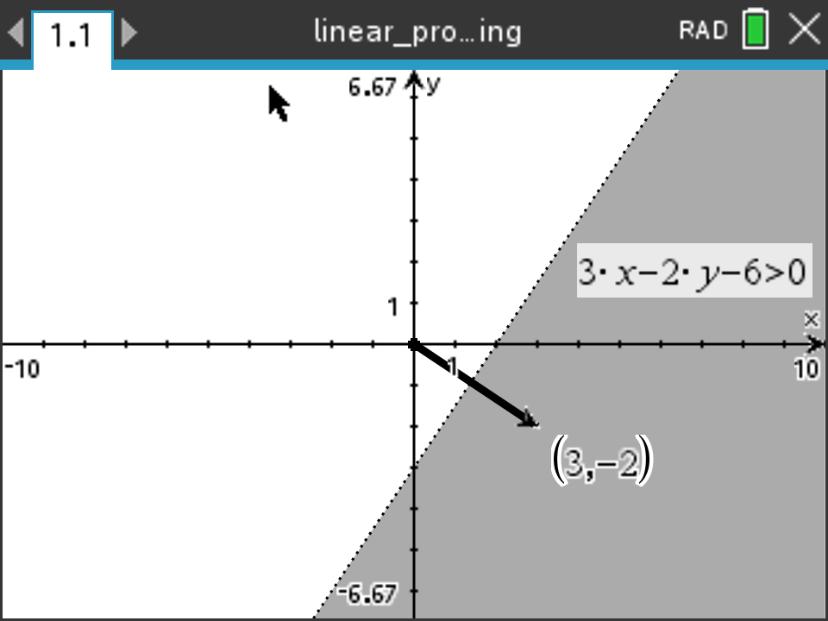
示例:1 求 \(3x-2y-6\) 的正区域并绘制之。
解: 如图 1 所示,直线 \(3x-2y-6=0\) 的法向量 \(\begin{bmatrix} 3\\-2 \end{bmatrix}\) 指向直线下方(也可称右下方)。
因此 \(3x-2y-6\) 的正区域位于直线 \(3x-2y-6=0\) 下方。☐
读者要锻炼在头脑中想象直线正负区域的能力。请先在头脑中想象以下问题的解答,然后用纸笔作答验证。
示例:2 求 \(2x+5y-1\) 的负区域并绘制之。
示例: 绘制 \(|x+2y|>3\) 的区域。
直线围成的区域
示例:3 平面直角坐标系中,不等式组 \(\begin{cases}x+y-2\geq0\\x-y+2\geq0\\x\leq2\end{cases}\) 表示的平面区域面积是多少?
示例:4 平面直角坐标系中,不等式组 \(\begin{cases}x\geq0\\x+3y\geq4\\3x+y\leq4\end{cases}\) 表示的平面区域面积是多少?
示例: 将适合不等式组 \(\begin{cases} 2x+y\leq7\\ 5x-3y\geq1\\ x-5y\leq9 \end{cases}\) 的点 \((x,y)\) 用图像表示,并求图像的面积。

解: 不等式组围成的区域如图 2 所示。
由两个平面向量组成矩阵的行列式的几何意义是这两个向量张成的平行四边形的面积(有向面积)。
取三角形的两条边向量 \(\begin{bmatrix} 5\\1 \end{bmatrix}\) 和 \(\begin{bmatrix} 3\\5 \end{bmatrix}\) , \(S_\triangle=\dfrac{1}{2}\begin{vmatrix} 5 & 3\\ 1 & 5 \end{vmatrix}=11\) 。☐
示例:5 在平面直角坐标系中,不等式组 \(\begin{cases}x+y-2\geq0\\x+2y-4\leq0\\x+3y-3\geq0\end{cases}\) 表示的平面区域的面积是多少?
示例:6 在平面直角坐标系中,若不等式组 \(\begin{cases}x+y-1\geq0\\x-1\leq0\\ax-y+1\geq0\end{cases}\) (\(a\)为常数)所表示的平面区域的面积等于 \(2\) ,则 \(a\) 的值为多少?
简单线性规划问题
线性规划问题
线性规划问题的标准型包括以下三个部分:
一个需要极大化的线性函数,例如:\(c_1 x_1 + c_2 x_2\)
以及如下形式的问题约束,例如:
\(\qquad\qquad\) \(a_{11} x_1 + a_{12} x_2 \le b_1\)
\(\qquad\qquad\) \(a_{21} x_1 + a_{22} x_2 \le b_2\)
\(\qquad\qquad\) \(a_{31} x_1 + a_{32} x_2 \le b_3\)
和非负变量,例如:\(x_1 \ge 0,\ x_2 \ge 0\)
示例: 某农夫有一块 \(A\) 平方千米的农地用以种植小麦或大麦 (\(S_1\) 和 \(S_2\) 平方千米)。该农夫只可以使用有限数量的肥料 \(F\) 和农药 \(P\) 。而单位面积的小麦和大麦都需要不同数量的肥料和农药,小麦以 \((F_1,P_1)\) 表示,大麦以 \((F_{2},P_{2})\) 表示。设小麦和大麦的售出价格分别为\(S_{1}\)和\(S_{2}\),则最佳种植面积问题可以表示为以下的线性规划问题:
\(\max\ \mathbf{Z}=S_1x_1+S_2x_2\) (目标函数:最大化利润)
s.t. \(x_1+x_2\leq A\) (种植面积的限制)
\(\qquad\) \(F_1x_1+F_2x_2\leq F\) (肥料数量的限制)
\(\qquad\) \(P_1x_1+P_2x_2\leq P\) (农药数量的限制)
\(\qquad\) \(x_1\geq0,\ x_2\geq0\) (不可以栽种负数面积)☐
示例: 已知约束条件 \(x+y\leq3,\ 3x+y\leq7,\ x+3y\leq7,\ x\geq0,\ y\geq0\) ,求目标函数 \(f(x,y)=5x+4y\) 的最大值。
解: 对于两个变量的线性规划问题,图像法是常见的解法。事实上中学阶段几乎只使用图像法求解
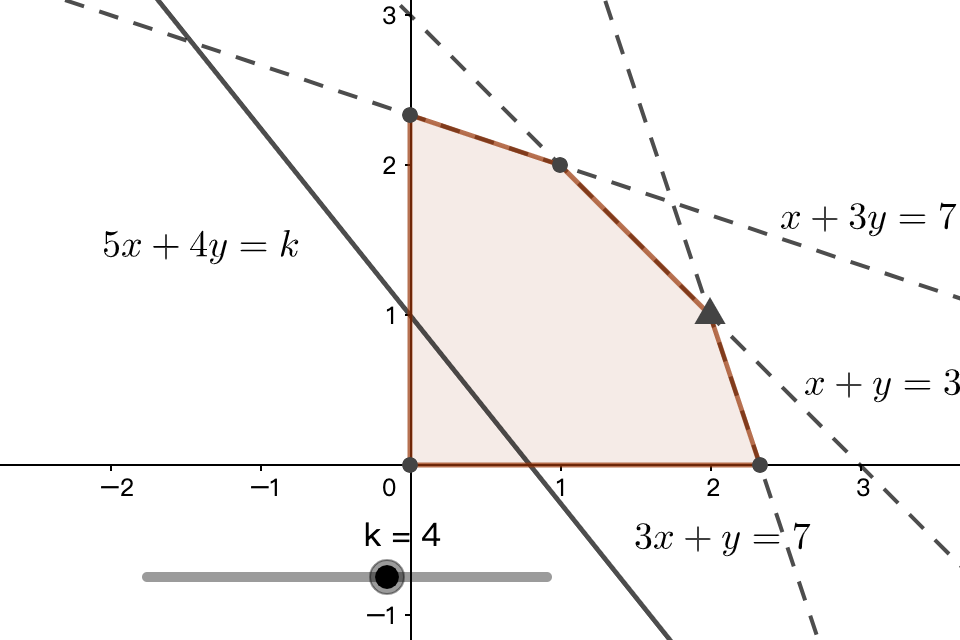
当 \(5x+4y=k\) 运动到 \(\blacktriangle\) 标记的点时, \(k\) 取到最大值 \(14\) 。
因此 \(x=2,y=1\) 时,目标函数取到最大值 \(14\) 。☐

示例:7 在约束条件 \(\begin{cases} x-4y\leq-3\\3x+5y\leq25\\x\geq1 \end{cases}\) 下求目标函数 \(f(x,y)=2x+y\) 的最大值和最小值。
含有参数的线性规划
示例:8 已知 \(a\geq0\) , \(x,y\) 满足约束条件 \(\begin{cases}x\geq1\\x+y\leq3\\y\geq a(x-3)\end{cases}\) ,若 \(z=2x+y\) 的最小值为 \(1\) ,则 \(a=\) ( ) 。
A. \(\dfrac{1}{4}\) \(\qquad\) B. \(\dfrac{1}{2}\) \(\qquad\) C. \(1\) \(\qquad\) D. \(2\)
示例:9 若 \(x,y\) 满足 \(\begin{cases}x+y-2\geq0\\kx-y+2\geq0\\y\geq0\end{cases}\) ,且 \(z=y-x\) 的最小值为 \(-4\) ,则 \(k\) 的值为 ( ) 。
A. \(2\) \(\qquad\) B. \(-2\) \(\qquad\) C. \(\dfrac{1}{2}\) \(\qquad\) D. \(-\dfrac{1}{2}\)
特殊的目标函数
示例:10 若 \(x,y\) 满足约束条件 \(\begin{cases} x-1\geq0\\ x-y\leq0\\ x+y-4\leq0 \end{cases}\) ,则 \(\dfrac{y}{x}\) 的最大值为 \(\_\_\_\_\_\_\_\_\) 。
示例:11 已知 \(\begin{cases} x\geq1\\ x-y+1\leq0\\ 2x-y-2\leq0 \end{cases}\) ,则 \(x^2+y^2\) 的最小值是 \(\_\_\_\_\_\_\_\_\) 。
习题
练习:12 若不等式组 \(\begin{cases}x\geq0\\x+3y\geq4\\3x+y\leq4\end{cases}\) 所表示的平面区域被直线 \(y=kx+\dfrac{4}{3}\) 分为面积相等的两部分,则 \(k\) 的值是 ( ) 。
A. \(\dfrac{7}{3}\) \(\qquad\) B. \(\dfrac{3}{7}\) \(\qquad\) C. \(\dfrac{4}{3}\) \(\qquad\) D. \(\dfrac{3}{4}\)
练习:13 记不等式组 \(\begin{cases}x\geq0\\x+3y\geq4\\3x+y\leq4\end{cases}\) 所表示的平面区域为 \(D\) 。若直线 \(y=a(x+1)\) 与 \(D\) 有公共点,则 \(a\) 的取值范围是 \(\_\_\_\_\_\_\_\_\)
练习:14 在坐标平面上,不等式组 \(\begin{cases}y\geq x-1\\y\leq-3|x|+1\end{cases}\) 所表示的平面区域的面积为 ( ) 。
A.\(\sqrt{2}\) \(\qquad\) B.\(\dfrac{3}{2}\) \(\qquad\) C.\(\dfrac{3\sqrt{2}}{2}\) \(\qquad\) D. \(2\)
练习:15 当 \(x\) 满足 \(0\leq x\leq 1\) 时,要使 \(y=ax+b\) 满足 \(0\leq y\leq1\) , \(a\)、\(b\) 应取怎样的值? \(a\) 、\(b\) 应取怎样的值?并以 \(a\) 、 \(b\) 为坐标,画出点 \(a\) 、 \(b\) 所在的范围。
练习: 在 \(x\geq0, y\geq0, 3x+y\leq3, 2x+3y\leq6\) 的条件下,试求 \(x-y\) 的最值。
练习:16 若 \(x,y\) 满足约束条件 \(\begin{cases}x-2y-2\leq0\\x-y+1\geq0\\y\leq0\end{cases}\) 则 \(z=3x+2y\) 的最大值为 \(\_\_\_\_\_\_\_\_\)
练习:17 满足约束 \(|x|+2|y|\leq2\) 的目标函数 \(z=y-x\) 的最小值是 \(\_\_\_\_\_\_\_\_\)
练习:18 设 \(m>1\) ,在约束条件 \(\begin{cases}y\geq x\\ y\leq mx \\x+y\leq1\end{cases}\) 下,目标函数 \(z=x+5y\) 的最大值为 \(4\) ,则 \(m\) 的值为 \(\_\_\_\_\_\_\_\_\) 。
练习:19 若变量 \(x,y\) 满足约束条件 \(\begin{cases}y\leq x\\x+y\leq4\\y\geq k\end{cases}\) ,且 \(z=2x+y\) 的最小值为 \(-6\) ,则 \(k=\_\_\_\_\_\_\_\_\) 。
练习:20 设 \(z=kx+y\) ,其中实数 \(x,y\) 满足 \(\begin{cases}x\geq2\\x-2y+4\geq0\\2x-y-4\leq0\end{cases}\) ,若 \(z\) 的最大值为 \(12\) 则实数 \(k=\_\_\_\_\_\_\_\_\) 。
练习:21 已知变量 \(x,y\) 满足约束条件 \(\begin{cases} x+2y-3\leq0\\ x+3y-3\geq0\\ y-1\leq0 \end{cases}\) ,若目标函数 \(z=ax+y\) (其中 \(a>0\) )仅在点 \((3,0)\) 处取得最大值,则 \(a\) 的取值范围为 \(\_\_\_\_\_\_\_\_\) 。
练习:22 设 \(x,y\) 满足约束条件 \(\begin{cases} x+y\geq1\\ x-y\geq-1\\ 2x-y\leq2 \end{cases}\) ,若目标函数 \(z=ax+2y\) 仅在点 \((1,0)\) 处取得最小值,则 \(a\) 的取值范围是 ( ) 。
A. \((-1,2)\) \(\qquad\) B. \((-4,2)\) \(\qquad\) C. \((-4,0]\) \(\qquad\) D. \((-2,4)\)
练习:23 \(\begin{cases} x-y-2\leq0\\ x+2y-4\geq0\\ 2y-3\leq0 \end{cases}\) ,则 \(\dfrac{y}{x}\) 的最大值为 \(\_\_\_\_\_\_\_\_\) 。
练习:24 已知变量 \(x,y\) 满足约束条件 \(\begin{cases} x-y+2\leq0\\ x\geq1\\ x+y-7\leq0 \end{cases}\) ,则 \(\dfrac{y}{x}\) 的取值范围是 ( ) 。
A. \(\left[\dfrac{9}{5},6\right]\) \(\qquad\) B. \(\left(-\infty,\dfrac{9}{5}\right]\cup\left[6,+\infty\right)\) \(\qquad\) C. \(\left(-\infty,3\right]\cup\left[6,+\infty\right)\) \(\qquad\) D. \(\left[3,6\right]\)
练习:25 若实数 \(x,y\) 满足 \(\begin{cases} x-y+1\leq0\\ x>0\\ y\leq2 \end{cases}\) ,则 \(\dfrac{y}{x}\) 的取值范围是 ( ) 。
A. \((0,2)\) \(\qquad\) B. \((0,2]\) \(\qquad\) C. \((2,+\infty)\) \(\qquad\) D. \([2,+\infty)\)
练习: 已知点 \(P(x,y)\) 的坐标满足条件 \(\begin{cases} x+y\leq4\\ y\geq x\\ x\geq1 \end{cases}\) 点 \(O\) 为坐标原点,那么 \(|PO|\) 的最小值等于 \(\_\_\_\_\_\_\_\_\) ,最大值等于 \(\_\_\_\_\_\_\_\_\) 。
练习:26 已知实数 \(x,y\) 满足 \(\begin{cases} x-2y+4\geq0\\ 2x+y-2\geq0\\ 3x-y-3\leq0 \end{cases}\) ,则 \(x^2+y^2\) 的取值范围是 \(\_\_\_\_\_\_\_\_\) 。
练习:27 若变量 \(x,y\) 满足 \(\begin{cases} x+y\leq2\\ 2x-3y\leq9\\ x\geq0 \end{cases}\) ,则 \(x^2+y^2\) 的最大值是 ( ) 。
A.\(4\) \(\qquad\) B.\(9\) \(\qquad\) C.\(10\) \(\qquad\) D.\(12\)
练习: 如果点 \(P\) 在平面区域 \(\begin{cases} 2x-y+2\geq0\\ x+y-2\leq0\\ 2y-1\geq0 \end{cases}\) 上,点 \(Q\) 在曲线 \(x^2+(y+2)^2=1\) 上,那么 \(|PQ|\) 的最小值为 ( ) 。
A. \(\dfrac{3}{2}\) \(\qquad\) B. \(\dfrac{4}{\sqrt{5}}-1\) \(\qquad\) C.\(2\sqrt{2}-1\) \(\qquad\) D. \(\sqrt{2}-1\)
练习: 设 \(D\) 是不等式组 \(\begin{cases} x+2y\leq10\\ 2x+y\geq3\\ 0\leq x\leq4\\ y\geq1 \end{cases}\) 表示的平面区域,则 \(D\) 中点 \(P(x,y)\) 到直线 \(x+y=10\) 距离的最大值是 \(\_\_\_\_\_\_\_\_\)