对称、变换和面积
“几何学 (Geometry) 是数学的一个基础分支,主要研究形状、大小、图形的相对位置等空间区域关系以及空间形式的度量。许多文明都发展出一些几何学,包括许多有关长度、面积和体积的知识。在公元前六世纪,西方世界开始将几何学视为数学的一部分。公元前三世纪产生了欧几里得几何学,这成为之后几个世纪的几何学标准。”1
对称和变换
“对称” (symmetry) 是日常生活中的一种常见现象。例如,我们的人体是左右对称的,北京旧皇城的布局是左右对称的,故宫和普通四合院等房屋建筑也是左右对称的。
对称是宇宙间最普遍、最重要的特性之一,近代科学表明几乎自然界的重要规律都与对称有关。远至天体形状、运行轨道;近如人类的胚胎发育等问题无一不与对称有关联。数学是人类从日常生活实践中抽象出来,并加以精炼和提高而形成的学科。对称现象也被提高凝练成了数学的一个分支。
轴对称和旋转对称
对称性的定义
- 将一个几何图形经过某种变换后,该图形依然占据相同的空间位置,我们就称这个图形具有某种对称性。
- 如果图形沿一直线翻转后仍然占据相同的空间位置,则称其是轴对称图形,该直线称为对称轴。
- 如果图形绕一点旋转一定角度后仍然占据相同的空间位置,则称其为旋转对称图形,该点称为旋转对称中心。
- 如果图形绕一点旋转 \(180^\circ\) 后占据相同的空间位置,则称为其为中心对称图形,该点称为对称中心。
♣请注意:我们这里给出的是“对称”在初等几何中的狭义定义。一般地,事物在某种变换下具有的不变性质就是对称性。对称性不仅仅是几何中的概念,在整个数学知识体系中处处都有对称性的体现。
思考与讨论
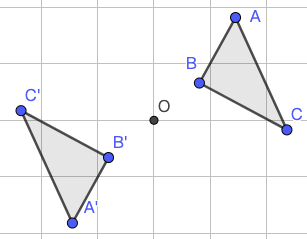
- 课本上有时也说“两个图形关于直线对称”、“两个图形中心对称”(如图 2 所示)。那是什么意思?
- 你能利用前述关于对称性的定义给出“两个图形轴/中心对称”的定义么?
- 你能绕开前述关于对称性的定义给出“两个图形轴/中心对称”的定义么?
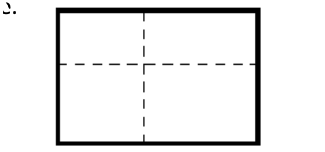
示例: 分析长方形的对称性。
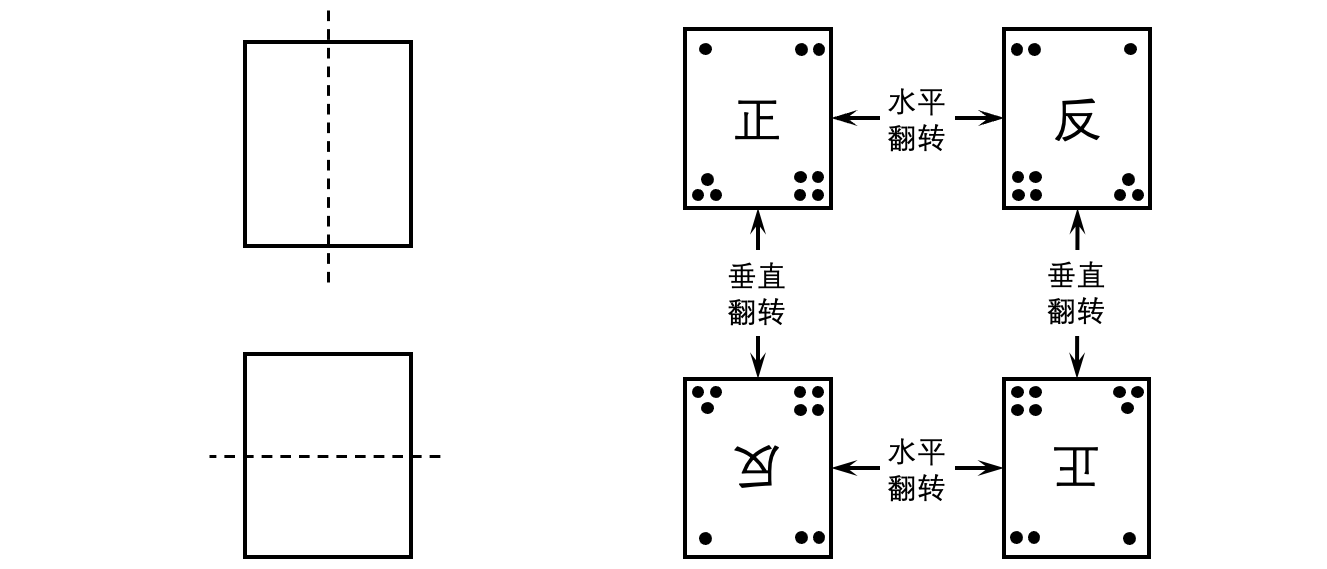
长方形是轴对称图形,有两条对称轴,如图 3 (左)所示。如果我们将长方形看作实体(四个角不同,有正反面),那么一个长方形可以以四种方式占据某个同样的位置。这四种方式可以由沿两条对称轴的翻转操作的组合得到,如图 (右)所示。
长方形同样是中心对称图形,对称中心就是对角线的交点。长方形绕中心旋转 \(180^\circ\) 后仍然占据相同的空间位置,如图 4 所示。
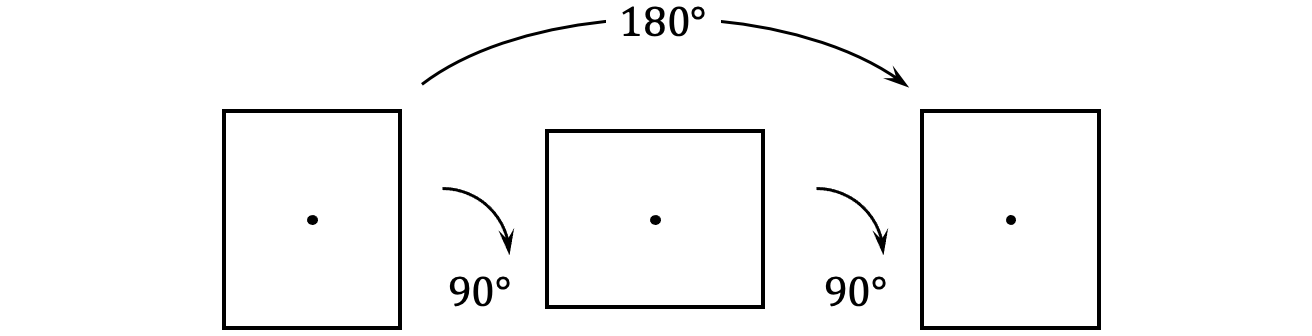
☐
思考与讨论
- 选定长方形的一条对称轴,使用对应的翻转操作,配合旋转操作,能够得到图 3 (右)所示的四种不同状态么?
- 你能使用一种翻转操作和旋转操作,画出图 3 (右)所示的状态转换图么?
思考与讨论
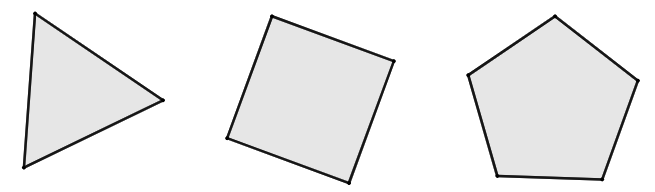
- 使用类似的方法分析正方形的对称性。
- 使用类似的方法分析正三角形的对称性。
- 使用类似的方法分析正五边形的对称性。
- 你能画出一个 \(90^\circ\) 旋转对称的非轴对称图形么?
示例:2 将正方形的纸折起来,扎一个洞再打开,纸上会出现图 6 所示的四个洞。请问纸的折痕可能是 ABCDE 中的哪个?
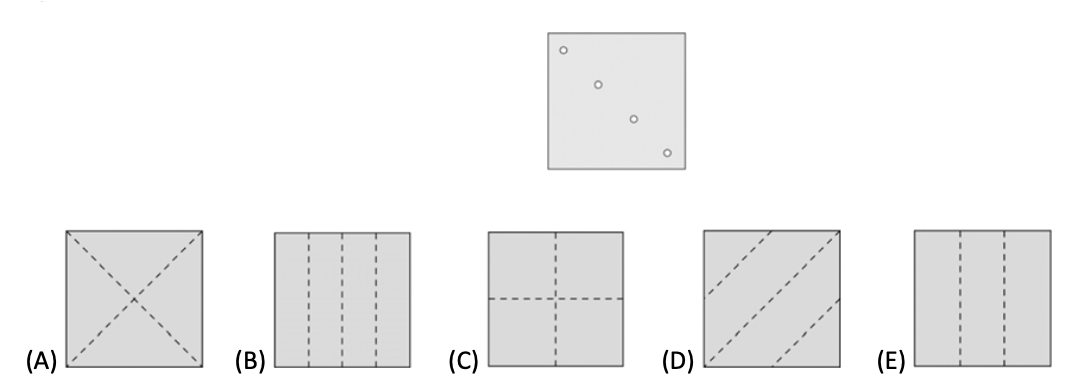
☐
思考与讨论
- ABCE 的折纸方法,展开后洞的位置如何?请在下面空白处画出示意图。

读一读
折纸的展开图计算在实际生产中很有意义,它是钣金工艺的数学基础之一。工程师通过对一整张金属片进行连续的折弯、冲压、打孔等操作后,能够制作出各种复杂的壳体。小到铁盒,大到汽车飞机的外壳,都是钣金工艺的用武之地。
示例: 根据给定对称轴,作出轴对称图形的另一半。
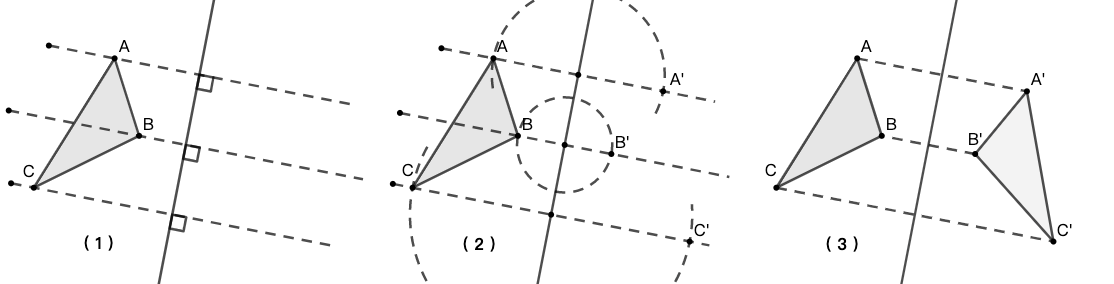
作图过程 以 \(\triangle{ABC}\) 为例,
- [(1)] 分别以三角形的各个顶点做对称轴的垂线,如图 8 (1) 所示。
- [(2)] 以垂足为圆心,垂足到对应顶点的距离为半径画圆,交线段另一侧于点 \(A^{\prime},B^{\prime},C^{\prime}\) 。
- [(3)] 连接 \(A^{\prime},B^{\prime},C^{\prime}\) 。
☐
作图原理
轴对称图形的对称轴分是对应点连线的中垂线。找到关键点(对于多边形来说就是顶点),然后连线即可。
示例: 找出轴对称图形(图 9 )的对称轴。
(请注意:你的作图工具限制在直尺和圆规)
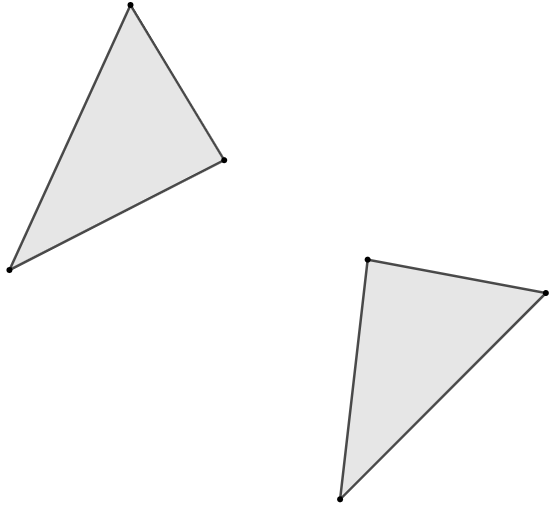
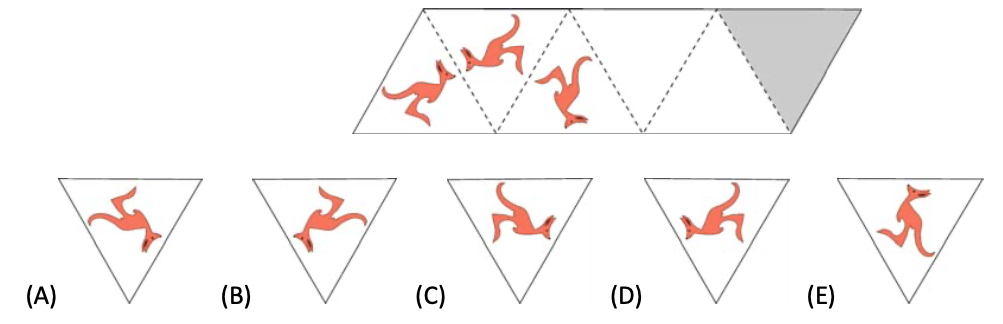
示例: 在图 10 中,虚线两侧的袋鼠是轴对称的。如果空白的三角形都画满袋鼠,那么阴影处的三角形的袋鼠是 ABCDE 中的哪一个样式?
分析 这类题目要求你在头脑中想象图案沿对称轴翻转后的样子。你在练习中应当反复在头脑中想象翻转的过程,直至你能够轻松操作这一过程。但在临场解题过程中你可以使用多种方法来辅助思考。
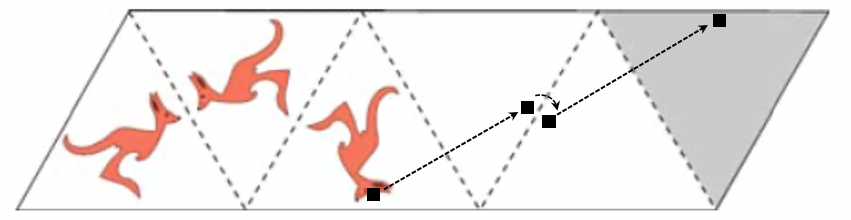
解: 一个可行的方法是标记出袋鼠头部的位置,考察头部不断进行对称操作后,最终在右侧的三角形位置中处于什么位置,如图 11 所示。
☐
思考与讨论
- 如果标记袋鼠的后腿而非头部,解题过程如何?
- 如果标记袋鼠的尾巴呢?
- 如果不允许在题目上涂画,你如何解题?
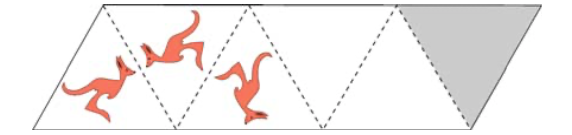
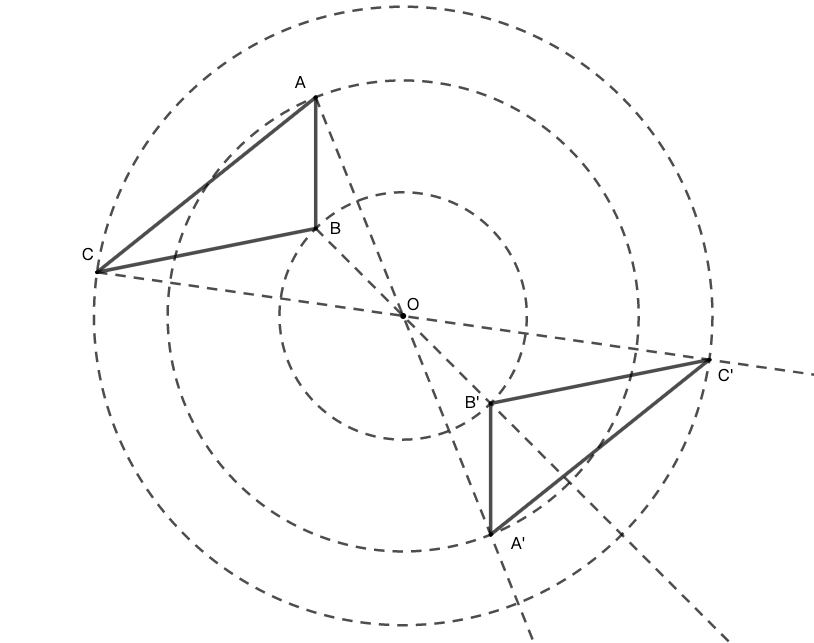
示例: 根据给定的对称中心,做出中心对称图形的另一半。以 \(\triangle{ABC}\) 和对称中心 \(O\) 为例,图 13 展示了作图过程。请读者自行补充作图过程的描述。
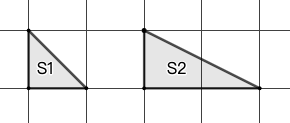
示例: 如果方格面积为 \(1\) ,求图 14 中三角形的面积。
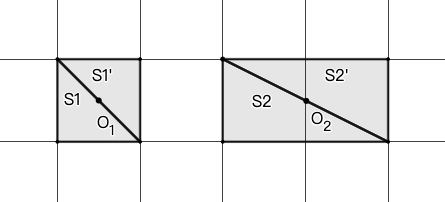
解: 虽然还没有学过三角形的面积公式,但我们完全有能力使用对称性来解决这个问题。如图 15 所示,这两个三角形可以由正方形和长方形沿对角线切割而来。切割出的每对三角形都是中心对称的,因此三角形的面积是对应的正方形或长方形面积的一半。
☐
思考与讨论
- 两个相同的直角三角形可以拼成矩形。你能据此给出直角三角形的面积公式么?
- 你能构造一个证明,说明为什么两个相同的直角三角形能拼成矩形么?\(\bigstar\bigstar\) (提示:这并不容易,你首先要退回到矩形的定义。)
平移和旋转
空间对称性
将整个空间平移或旋转,物理规律保持不变。

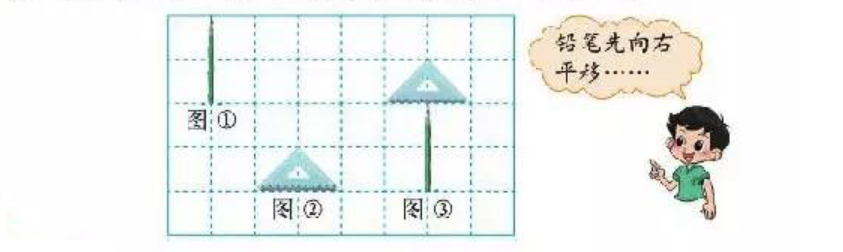
空间对称性是我们讨论一切问题的出发点,这一重要性质在在三年级下学期的数学课本上(北师大版)隐含给出。图 17 摘自教材第 28 页,你可以看到,图中的铅笔无论是竖直还是水平,无论是放在左上还是右下,都占据两个格线的长度。
示例: (乘法交换律)用底边乘以高长方形的面积。无论将长方形竖直还是水平放置,都会得到相同的结果。
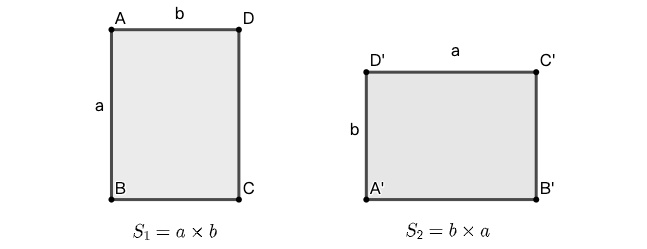
示例: (乘法结合律)用底面乘以高计算立方体的体积。无论将立方体如何放置于平面,都会得到相同的结果。
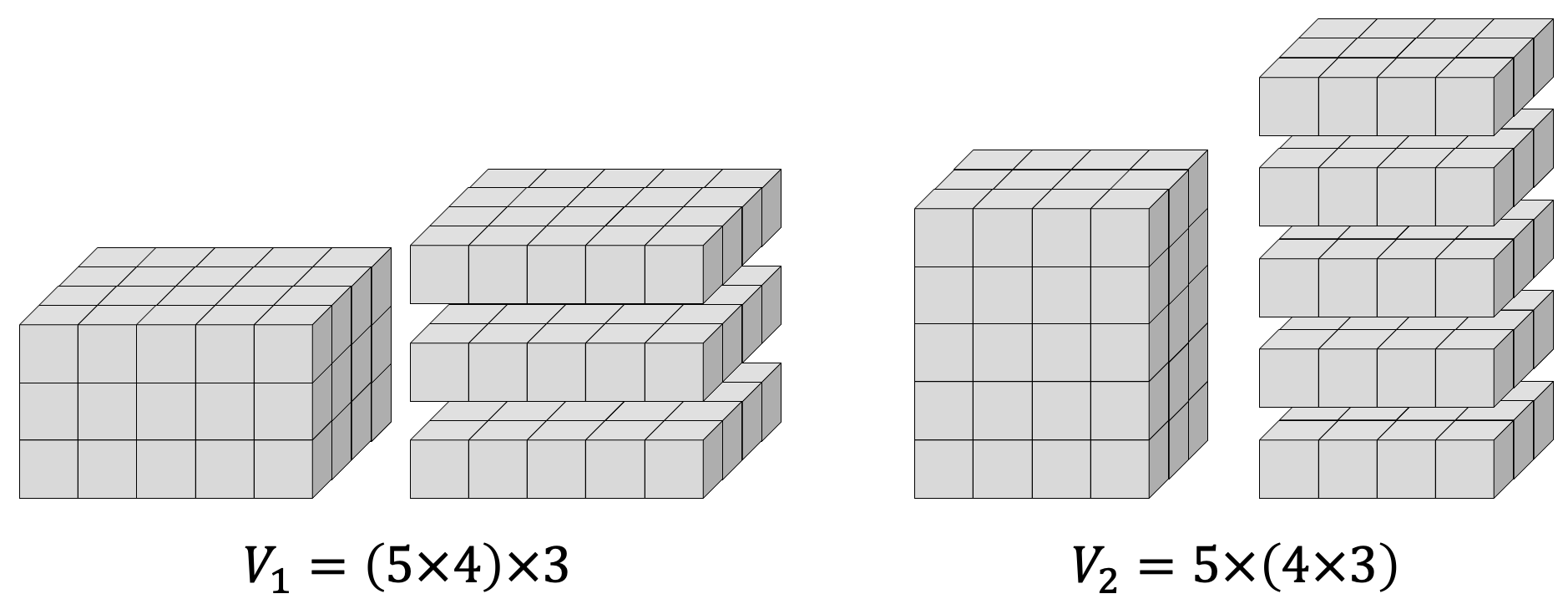
思考与讨论
- 你能用几何图形说明加法交换律么?
- 你能用几何图形说明加法结合律么?
数量
数量是对客观事物的抽象表达方式。人类创造了关于数量的语言,以此来表达事物的多少。平面图形的数量是用长度、面积和角度等概念表示的。
测量单位
《孔子家语》曰:“布指知寸,布手知尺,舒肘知寻。”
古埃及人最初也是用身体的一部分作为测量单位。古埃及的测量单位腕尺是指从肘到中指端的距离。公元 \(9\) 世纪时,英王亨利一世以自己鼻尖到食指尖的距离作为长度单位码(yard)。\(13\) 世纪,英王约翰以自己的足长为英尺 (foot) 。公元前 \(2\) 世纪,秦始皇制订了中国统一的度量衡(长度、容器和重量),以 \(10\) 寸为 \(1\) 尺,以 \(10\) 尺为 \(1\) 丈。 \(1\) 丈约为 \(231\) 厘米。
今天的公制单位米 (meter) 是法国人提出的。最初法国科学院将经过巴黎的地球子午线长度的千万分之一定义为 \(1\) 米。今天人们用真空中的光速来定义米:光在真空中 \(1/299792458\) 秒内行进的距离为 \(1\) 米。
思考与讨论
- 为什么用光速定义“米”时,用 \(1/299792458\) 这样一个数?
- 在光速定义中使用到了“秒”,秒又是如何定义的呢?
测量单位只是人类用来描述自然的手段,无论采用哪种单位都不会改变数学的本质。比如无论是用英尺还是米测量,正方形的周长都是边长的 \(4\) 倍,圆的周长和直径之比都是 \(\pi\) 。
带单位数量的计算
- 长度可以相加,得到更长的长度: \(4m+2m=6m\)
- 长度可以乘以数,得到数倍的长度: \(2m\times3=6m\)
- 长度可以乘以长度,得到面积: \(2m\times3m=6m^2\)
如果长度的单位不同,也可以相加或相乘,只是要进行单位转换,例如长度的相加:\(100cm + 2m = 1m + 2m = 3m\) 。再比如长度的相乘:\(200cm\times3m=2m\times3m=6m^2\) 。
思考与讨论
- 上述计算的几何意义是什么,你能画出对应的图形么?
- 上述加法的逆运算是什么,对应的几何含义是什么?
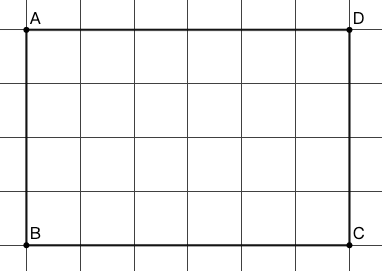
- 求图 20 所示长方形面积,以下算式的含义分别是什么?
\(4cm\times6cm\) \(4cm^2\times6\)\(4\times6cm^2\)
比例尺和图形标注
事物往往很大,无法按照实际大小绘制,于是人们绘制缩小的图形。
比例尺
比例尺是表示图上一条线段的长度与其实际长度之比。比例尺通常有三种表示方法:
- 数字式:用数字的比例式或分数式表示比例尺的大小。例如:\(1:50,000,000\) 或 \(1/50,000,000\) 。
- 线段式:在图上画一条线段(如 \(1cm\) ),并注明该线段所代表的实际距离。
- 文字式:直接用文字写出图上 \(1cm\) 代表实际距离是多少。
示例: 按 \(1:20\) 的比例尺将实际大小为 \(80cm\times120cm\) 的长方形绘制于纸上。
解: 图 21 绘制了该长方形。在图中一个小方格的边长为 \(1cm\) 根据 \(1:20\) 的比例尺,这代表实际大小的 \(20cm\) 。所以 \(80cm\times120cm\) 在图中占据 \(4cm\times6cm\) 即 \(4\) 格宽 \(6\) 格长。☐
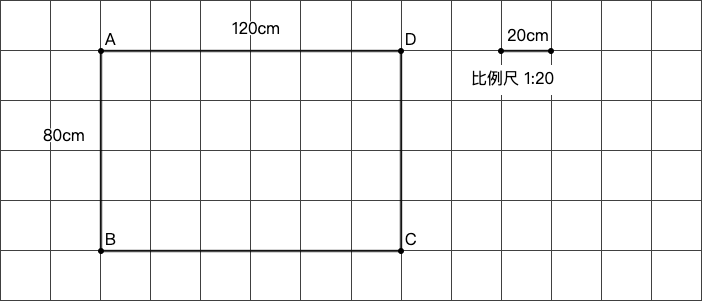
♣在进行尺寸标注时,应当标注实际的尺寸而非图纸上的尺寸。例如在上述示例中,长方形的长度应当标注为 \(120cm\) 而非 \(6cm\) 。
有时候我们在绘制一些草图时,往往并不能按照实际的比例进行绘制,但尺寸标注应当准确。你在数学试题中会经常看到这样的图形。你直接拿尺子在图上量是得不到正确结果的。你需要理性地计算,或者重绘准确的图形。
拿尺子量一量,得到一个大概的结果,然后顺着结果去计算或证明。这并不是投机取巧,这其实正是数学家最初认识客观规律基本手段。
示例: 图 22 给出了一个尺寸不是很合适的图形,但尺寸标注是准确的。计算出未标注线段的长度,自选比例尺,在图 中绘制比例准确的图形。
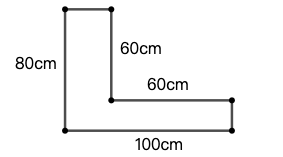

思考与讨论
- 选定不同的比例尺绘制图形时,有哪些要素是不变的?
- 找一份你所在市的地图,比例尺是多少,计算一下你家门口街道的实际长度。
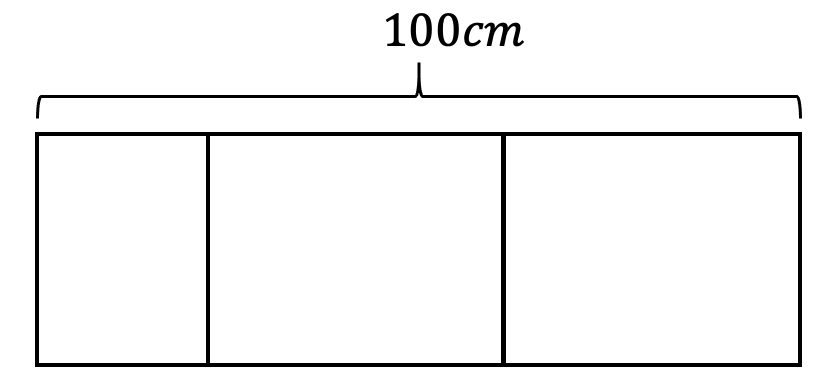
你有时会看到如图 24 所示的标注方式,这种方式往往用来消除标注歧义。比如图中的大括号表示 \(100cm\) 代表的是总长而非中间部分的长度。如何画好大括号是一个挑战,需要多加练习。请尝试在下面空白处照抄图 ,尤其要注意优雅地绘制大括号标记。
等量的运算
在解题中,常用到以下规则:
数量的运算规则
- 等量加等量,其和仍相等。
- 等量减等量,其差仍相等。
- 整体等于部分之和。
示例: 现代家具店的家具都是模块化拼装的。用同样的基本形状拼成不同的家具。图 25 展示了家具店出售的三人沙发、双人沙发和单人沙发的平面俯视图(从上面看下去的样子)。三人沙发宽 \(220cm\) ,双人沙发宽 \(160cm\) 。请问单人沙发的宽度是多少?
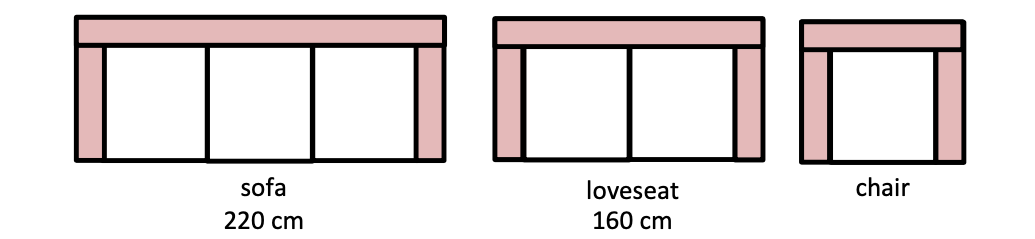
解: 三个沙发面和两个扶手(三人沙发)的宽度等于 \(220cm\) ,两个沙发面和两个扶手(双人沙发)的宽度等于 \(160cm\) 。这是题目中给出的两个等量关系,利用“等量减等量,其差仍相等”的运算规则,得到图 26 所示结果。
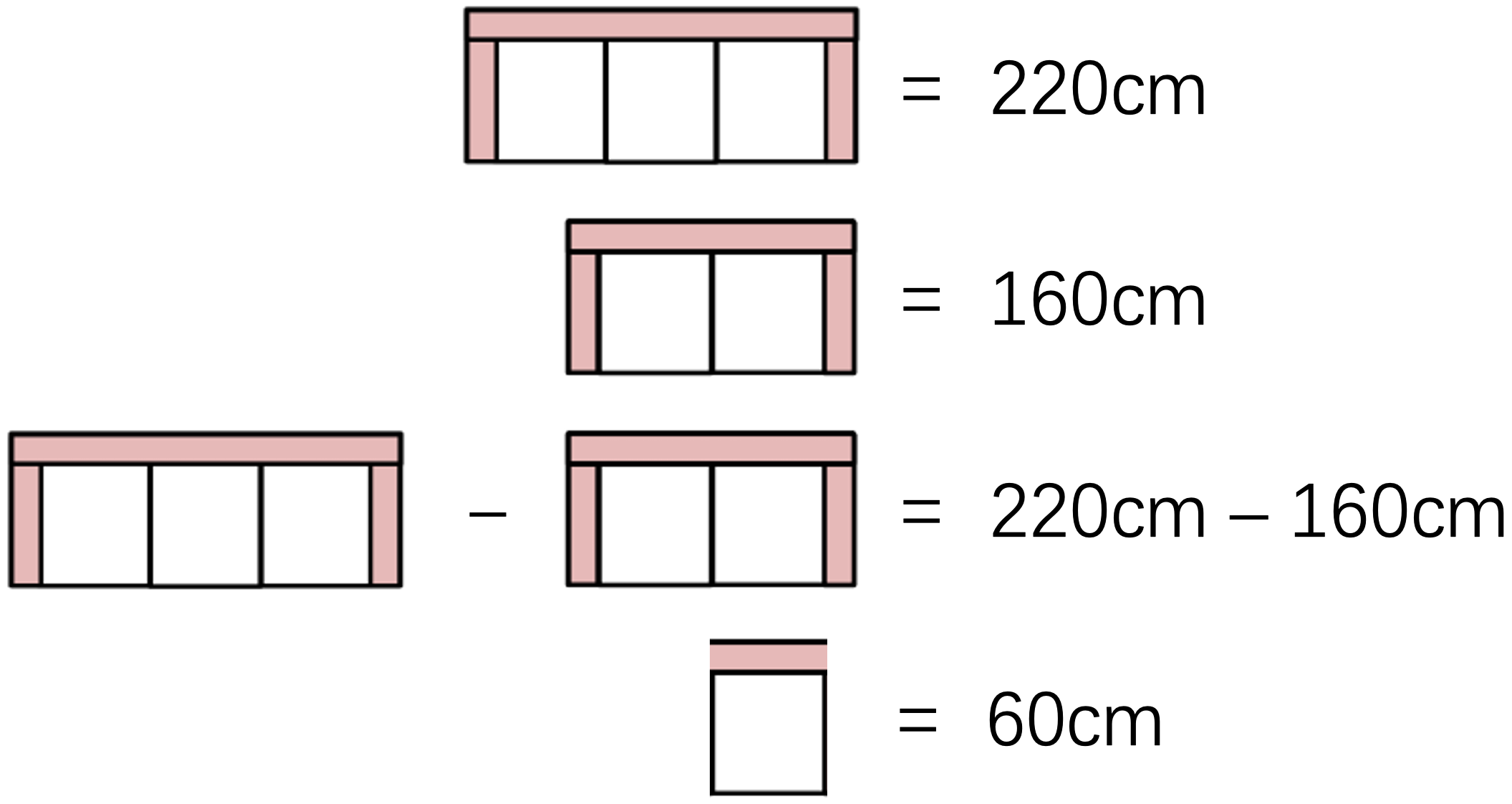
☐
思考与讨论
- 你能用字母表示沙发面和扶手的宽度,重写上述等式计算过程么?
示例: 求图 27 所示三角形 \(ABC\) 的面积。(小方格面积为 \(1\) )
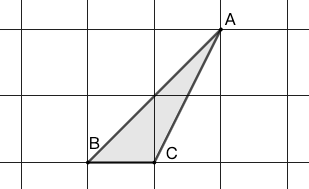
解: 用 \(2\times2\) 正方形,减去两个直角三角形的面积,就可以得到 \(\triangle ABC\) 的面积。

☐
示例: 两张长方形的纸片宽度相同。紧挨着放置时(如图 29 左侧所示),拼成的长方形面积之和为 \(100cm^2\) 。重叠放置时,大的纸片露出的部分面积是 \(20cm^2\) 。请问两张纸片的面积分别是多少

解: 两张纸片的面积之和是 \(100cm^2\) ,面积之差是 \(20cm^2\) 。我们可以根据题意将题图画为如图 28 所示图案。可知如下数量关系: \[20cm^2+S_2+S_2=100cm^2\]
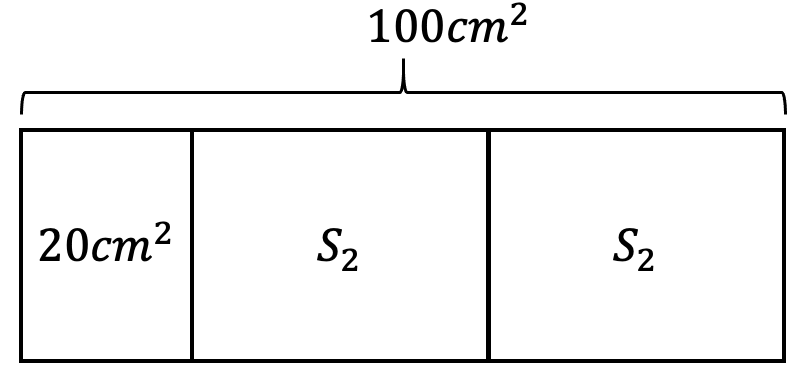
进一步求得小纸片的面积为 \(S_2=(100cm^2-20cm^2)/2=40cm^2\)
大纸片的面积为 \(S_1=S_2+20cm^2=60cm^2\) 。☐
变化图形中的不变量
有时候题目的条件不能将图形唯一确定,这时你需要更多的技巧和观察力。解决这类题目主要有
求解图形不变量的技巧
- 既然条件不能将图形唯一确定,那么图形是如何变化的?
- 画出在给定条件下的几个不同图形,观察所要求的值。你往往能发现图形的变化并不改变这些值。
- 你能够给出一个“极限状态”的图形么?这往往会让计算变得特别简单。
- 如果是选择题,你可以直接得到一个数。但对于完整的解题,你还需要构建一个严格的过程。
当你面对比较简单的题目时,你可以直接看题目的窍门所在。不过总有一些题目位于你能力的边缘,这时上面的技巧会给你很大的帮助。上面的技巧不仅仅用于解题,它们能让你更好地体会空间结构。
示例: 图 31 中 \(ABCD\) 为正方形,边长为 \(5cm\) 。阴影部分为矩形,求阴影部分的周长。
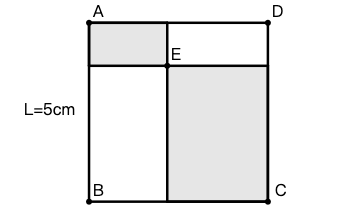
解: 本题的条件没有唯一确定图形,图 32 给出了三种可能的图形。然而稍微数一下格子就可以发现,阴影部分的周长均为 \(20cm\) 。于是我们可以猜测答案为 \(20cm\) 。
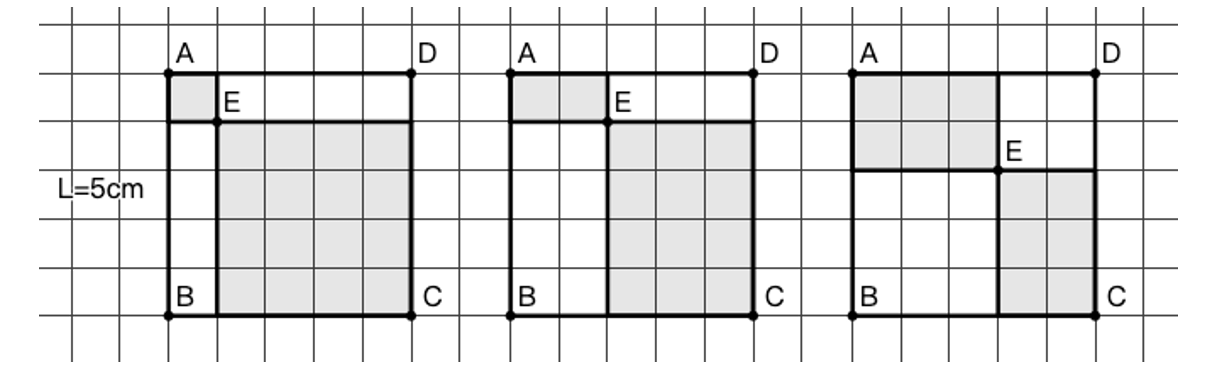
- 你能够画出 \(E\) 点处于某种“极限位置”的图形,验证上述猜测么?
- 你能够构建一个证明,说明无论 \(E\) 点取正方形 \(ABCD\) 内的哪一点,阴影部分的面积都是 \(20cm\) 么?

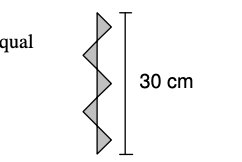
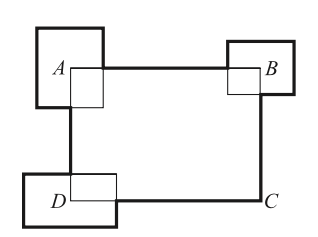
示例: 长方形 ABCD 的周长是 \(30cm\) 。有另三个长方形的中心为点 A, B 和 D (如图 33 所示)。这三个 长方形(其中心分别为点 A, B 和 D 者)的周长之和是 \(20cm\) 。请问粗线的总长度是多少?
问题: Karla 透过窗户看到一面迎风飘动的长方形旗帜,如果旗帜完好,那么下面 ABCDE 五幅图中,哪一个图案是她不可能看到的。

问题: 如图 35 所示,左侧图案折叠起来是 ABCDE 中的哪个?

问题: 图 36 中,剪纸打开后的形状是 ABCDE 中的哪个?

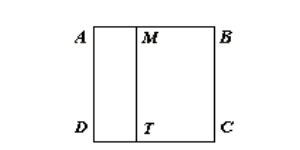
问题: 如图 37 所示, \(ABCD\) 是正方形,边长为 \(10cm\) 。 \(AMTD\) 是长方形,短边长度等于 \(3cm\) 。问正方形 \(ABCD\) 的周长比长方形 \(AMTD\) 长多少?
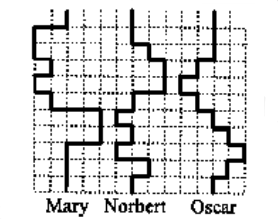
问题: 如图 38 所示, Mary 、 Norbert 和 Oscar 进行袋鼠跳游戏,他们沿着粗线所示路径前进。如果三人同时出发,并且前进速度相同,以下说法哪个正确?
- [A.] Mary 和 Oscar 同时到达。
- [B.] Norbert 最后到达。
- [C.] Oscar 先到达。
- [D.] \(3\) 人同时到达。
- [E.] Mary 和 Norbert 同时到达。
问题: 如图 39 所示,每个小方格的面积为 \(1\) 。请问图示字母 N 的面积是多少?

问题: 如图 40 所示, I II III IV 都是正方形。 I 的边长是 \(16m\) , II 的边长是 \(24m\) 。请回答以下问题:
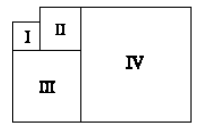
- [a.] IV 的周长是多少?
- [b.] 整个图形的周长是多少?
问题: 图 41 中哪个图案的长度最长?
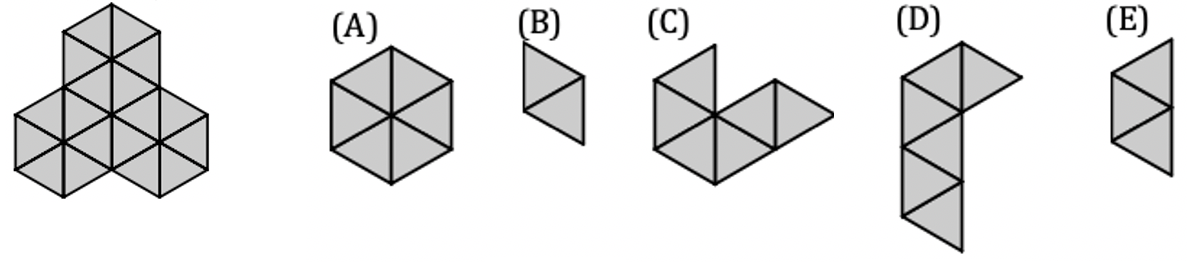
问题: 图 42 中哪一个图案面积最大?

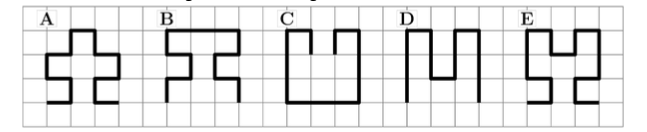
问题: Mike 希望用一组同样的图形拼出图 43 中拼出左侧的图形(比如可以用 \(18\) 个小三角形)。请问他无法用 ABCDE 中的哪个样式拼出左侧的图形?
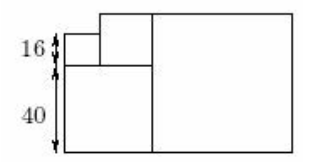
问题: 图 63 由四个正方形组成。其中两个正方形的边长分别为 \(16\) 和 \(40\) ,如图所示。最大的正方形的边长是多少?
问题: 图 45 中,\(AC=10m\), \(BD=15m\), \(AD=22m\)。求 \(BC\) 的长度。

问题: 求图 46 中 \(x\) 标记的线段长度。
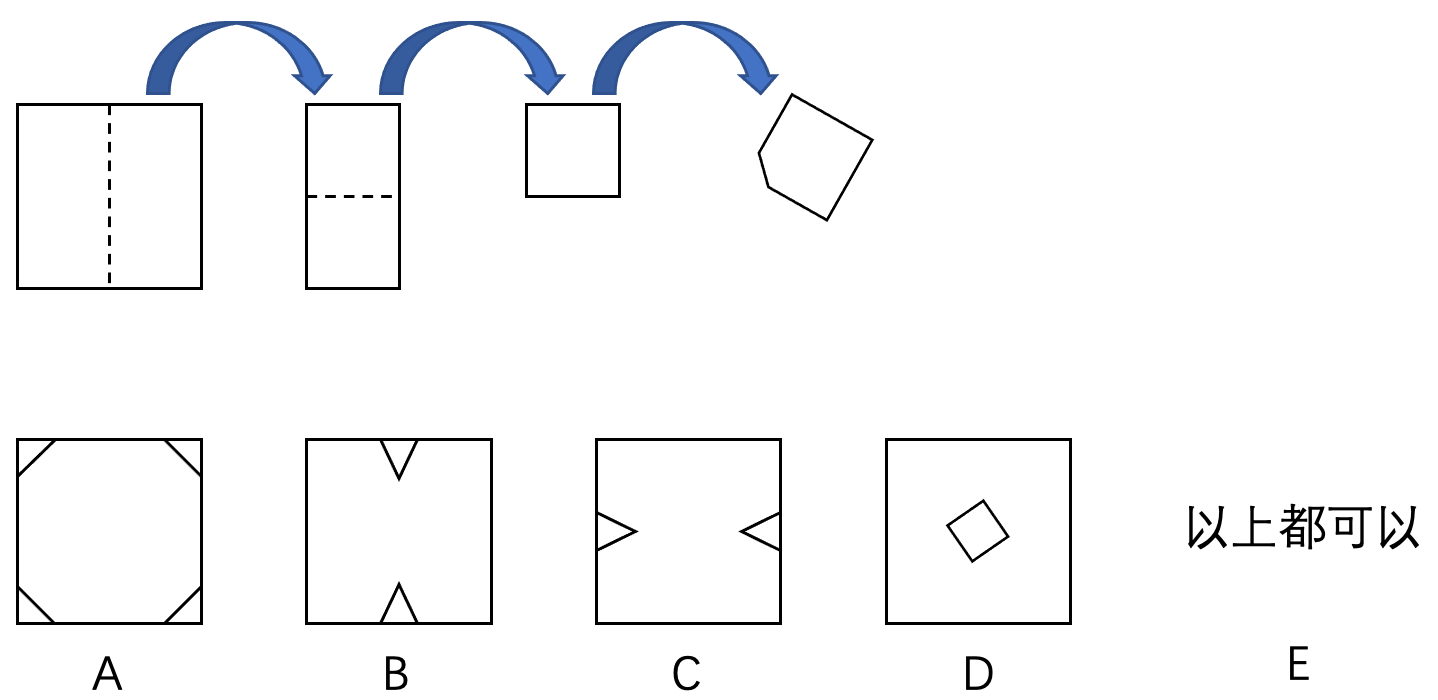
问题: 将一个正八边形的纸片对折三次得到一个三角形,如图 47 所示。然后如图减去顶点,减掉的部分呈直角三角形。请问纸片打开后是什么样子?
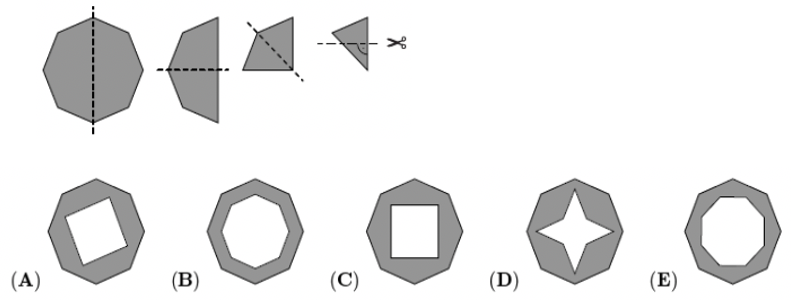
问题: 如图 48 所示, 1 2 3 4 四个图形中的哪两个拼起来可以正好填补左侧正方形的空白?
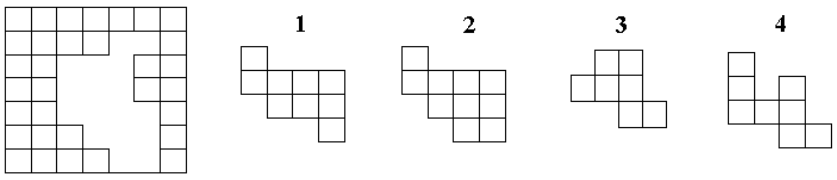
问题: Karl 要把图 49 左侧所示的纸片沿格线剪开,完美剪成右侧的两种 L 形状的小纸片(剪完不能剩下边角料)。请问 Karl 可以剪出几个 3 格方格的 L 形状。
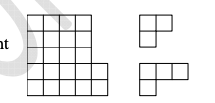
A. 1 B. 2 C. 3 D. 4 E. 无法完美剪成两种 L 型
问题: 两个 \(9cm\times9cm\) 的正方形重叠成一个 \(9cm\times13cm\) 的长方形,如图 50 所示。每个正方形重叠的部分面积有多大?
问题: 图 51 由七个正方形组成。请问最大的正方形的面积是最小的正方形面积的多少倍?
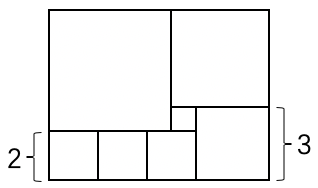
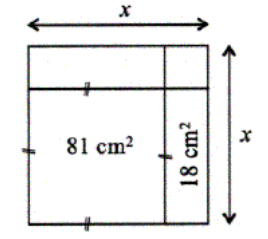
问题: 图 52 中,正方形 \(ABCD\) 由四个同样的长方形和一个正方形组成。每个长方形的周长是 \(40cm\) 。请问正方形 \(ABCD\) 的面积是多少?
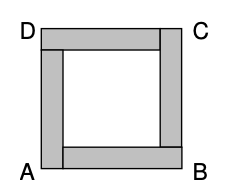
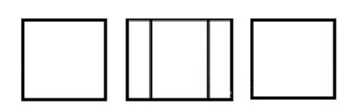
问题: Kelly 有一根 \(27cm\) 长的纸带。她将纸带分为四个长方形,将两对长方形中心画线连接,如图 53 所示。请问两条线段长度的总和是多少?

A. \(12cm\) B. \(13.5cm\) C. \(14cm\) D. \(14.5cm\) E. 长度不定
问题: 如图 54 所示,四条纸带宽度均为 \(10cm\) ,长度依次相差 \(25cm\) ,拼成图示左侧的图形和右侧的图形。请问两个图形周长相差多少?
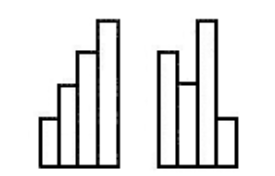
A. \(0cm\) B. \(20cm\) C. \(40cm\) D. \(50cm\) E. \(25cm\)
问题: 用两块图 55 中左侧的 L 型纸片,能拼出右侧四个形状中的几个?
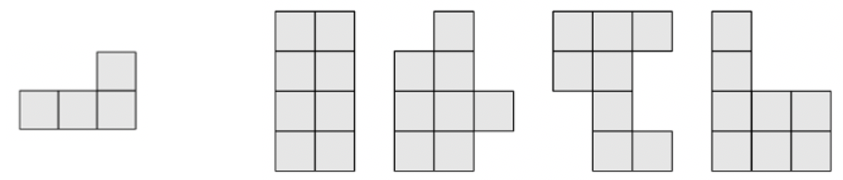
A. 0 B. 1 C. 2 D. 3 E. 4
问题: 如图 56 最右侧的图案所示,上面的硬币紧贴着下面的硬币滚动到右侧,硬币之间没有相对滑动。请问滚动之后的硬币图样是 ABCD 中的哪一个,或是如 E 所述取决于滚动速度?

问题: 如图 57 所示有四个齿轮,齿数分别是 \(30\) 、\(15\) 、\(60\) 和 \(10\) 。当最左侧的齿轮转过一圈后,最右侧的齿轮转了多少圈?

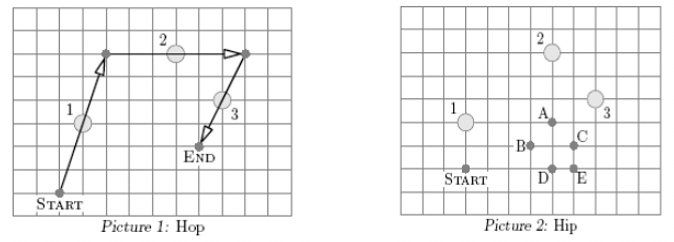
问题: 袋鼠Hip 和 Hop 在玩跳石头游戏。它们在地上放置了一些石头,依次跳过这些石头。规则是每一跳的路线正中都恰好有石头。图 58-1 是袋鼠 Hop 跳过的路径。袋鼠 Hip 换了个起点,如图 -2 所示。请问袋鼠 Hip 三跳后落在哪里?
问题: Peter 希望把图 59 所示的 \(7\times6\) 网格纸沿格线剪成若干个正方形。他最少能剪成几个正方形?(要求剪开的所有部分都是正方形)

A. 4 B. 5 C. 7 D. 9 E. 42
问题: 任选两个三角形,将它们任意重叠起来。重叠的部分不能是什么形状?
A. 三角形 B. 四边形 C. 五边形 D. 六边形 E. 以上都可以
问题: 将一张纸对折再对折,然后裁去一个角,如图 60 所示。展开后,选项中的哪个图样是无法得到的?
问题: 一张长方形的纸的尺寸为 \(192mm\times84mm\) 。一刀把纸裁成两个矩形,其中一个是正方形。然后再裁那个不是正方形的部分,也是一刀裁成两部分,其中一个是正方形。如此周而复始,直到全是正方形。请问最小的正方形的边长是多少?
A. \(1mm\) B. \(4mm\) C. \(6mm\) D. \(10mm\) E. \(12mm\)
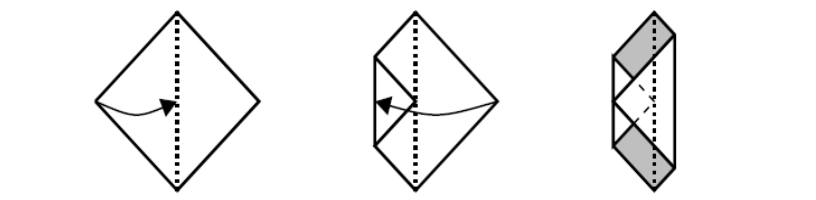
问题: 将正方形纸片如图 61 所示对折。如果原来正方形纸片的面积是 \(64cm^2\) ,请问阴影部分面积是多少?
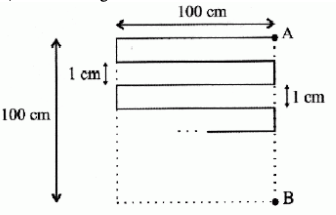
问题: 图 62 中从 A 到 B 的折线长度是多少?
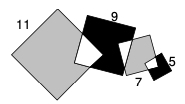
问题: 图 63 由四个正方形交叠而成。请问灰色部分总面积比黑色部分总面积大多少?
问题: 将一个大矩形剪成四个小矩形,如图 64 所示。其中三个矩形的周长分别是 \(11\) , \(16\) 和 \(19\) 。另一个矩形的周长既不是最大的也不是最小的。请问原来大长方形的周长是多少?
A. 30 B. 40 C. 38 D. 32 E. 28
问题: 图 65 中包含 \(5\) 个一样的等腰直角三角形。它们的总面积是多少?