用导数研究函数
微分学基本定理
定理: (波尔查诺-柯西中值定理)如果一个函数在一个闭区间上连续,并且在其两端点取异号的值,则该函数在该闭区间上有零点。
定理: (魏尔斯特拉斯最大值定理)在闭区间上连续的函数在该闭区间上有界。这时,在闭区间上既有使函数取最大值的点,也有使函数取最小值的点。
命题: (单调函数的连续性准则)闭区间 \(E=[a,b]\) 上的单调函数 \(f:E\rightarrow\mathbb{R}\) 在 \(E\) 上连续的充要条件是它的值集 \(f(E)\) 本身是以 \(f(a)\) 和 \(f(b)\) 为端点的闭区间。
引理: (费马引理) 如果函数 \(f:E\rightarrow\mathbb{R}\) 在内极值点 \(x_0\in E\) 可微,则它在该点的导数等于零:\(f'(x_0)=0\)
命题: (罗尔定理)如果函数 \(f:[a,b]\rightarrow\mathbb{R}\) 在闭区间 \([a,b]\) 上连续,在开区间 \((a,b)\) 上可微,并且 \(f(a)=f(b)\) 则必定存在 \(x_0\in(a,b)\) 使得 \(f'(x_0)=0\) 。
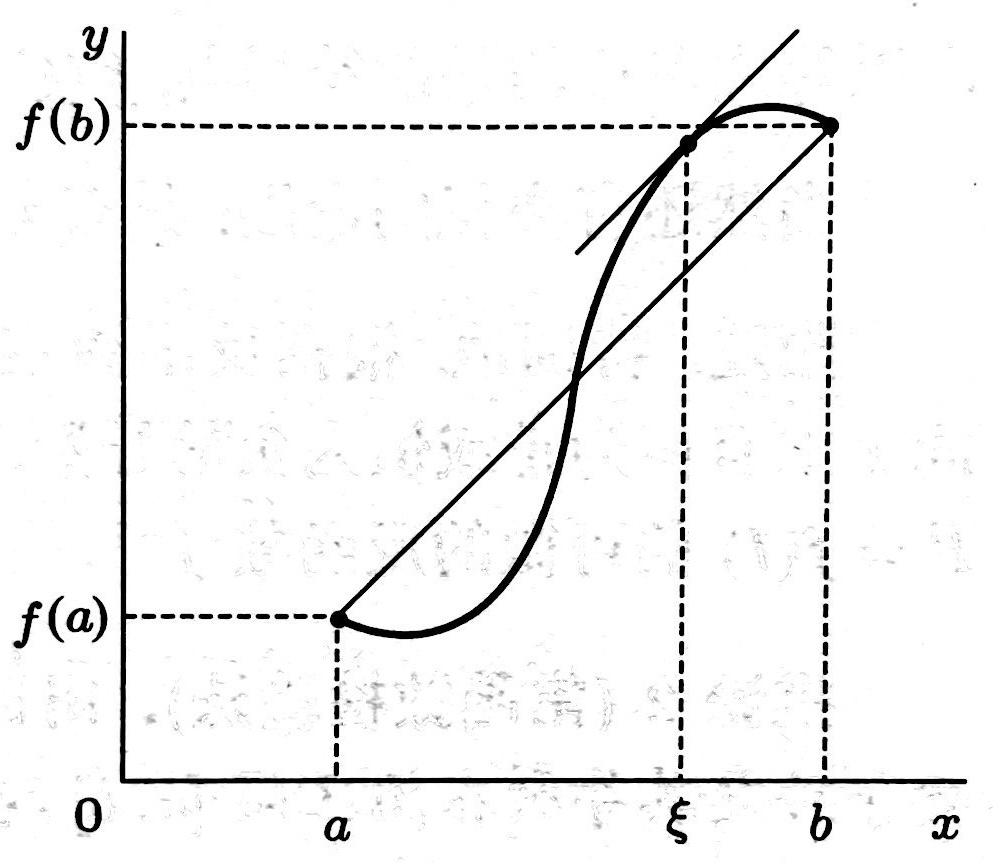
定理: (拉格朗日中值定理)如果函数 \(f:[a,b]\rightarrow\mathbb{R}\) 在闭区间 \([a,b]\) 上连续,在开区间 \((a,b)\) 上可微,则满足以下条件的点 \(x_0\in(a,b)\) 必定存在:\[\boxed{f(b)-f(a)=f'(x_0)(b-a)}\]
☐
推论: 路程的总长度不可能超过速度的最大值与通过这段路程所用的时间之积。这句话可以更准确地写为以下形式:\[\boxed{|f(b)-f(a)|\leq\sup_{t\in(a,b)} |f'(t)||b-a|}\]
推论: (函数单调性检验法 )如果函数在开区间上任何点的导数都是非负的(正的),则函数在这个开区间上不减(递增)。
推论: (常函数检验法 )闭区间 \([a,b]\) 上的连续函数在此区间上为常数的充要条件是其导数在闭区间 \([a,b]\) (甚至开区间 \((a,b)\))的任何点都等于零。
推论: 如果两个函数 \(F_1(x),F_2(x)\) 的导数 \(F_1'(x),F_2'(x)\) 在某区间上相等,即 \(F_1'(x)\equiv F_2'(x)\) ,则差 \(F_1(x)-F_2(x)\) 是常函数。
命题: (柯西有限增量定理)设 \(x=x(t)\) 和 \(y=y(t)\) 是在闭区间 \([\alpha,\beta]\) 上连续且在开区间 \((\alpha,\beta)\) 上可微的函数,则满足以下条件的点 \(\tau\in(\alpha,\beta)\) 存在:\[x'(\tau)(y(\beta)-y(\alpha))=y'(\tau)(x(\beta)-x(\alpha))\] 如果对于任何 \(t\in(\alpha,\beta)\) 还有 \(x'(t)\neq0\) ,则 \(x(a)\neq x(\beta)\) ,并且成立等式:\[\dfrac{y(\beta)-y(\alpha)}{x(\beta)-x(\alpha)}=\dfrac{y'(\tau)}{x'(\tau)}\]
定义: (泰勒多项式)以下代数多项式称为函数 \(f(x)\) 在点 \(x_0\) 的 \(n\) 阶泰勒多项式: \[P_n(x_0;x)=P_n(x)=f(x_0)+\dfrac{f'(x_0)}{1!}(x-x_0)+\cdots+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n\]
定义: (泰勒公式的余项)多项式 \(P_n(x)\) 与函数 \(f(x)\) 之间的偏差 \(f(x)-P_n(x_0;x)=r_n(x_0;x)\) 经常称为泰勒公式的余项,或更确切地称为泰勒公式的 \(n\) 阶余项: \[\boxed{f(x)=f(x_0)+\dfrac{f'(x_0)}{1!}(x-x_0)+\cdots+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+r_n(x_0;x)}\]
定理: 如果函数 \(f\) 和它的前 \(n\) 阶导数在以 \(x_0,x\) 为端点的区间上连续,并且 \(f\) 在该区间的内点有 \(n+1\) 阶导数,则对于在这个闭区间上连续并且在其内点有不为零的导数的任何函数 \(\phi\) ,都可以求出介于 \(x_0\) 和 \(x\) 之间的点 \(\xi\) ,使得\[\boxed{r_n(x_0;x)=\dfrac{\varphi(x)-\varphi(x_0)}{\varphi '(\xi)n!}f^{(n+1)}(\xi)(x-\xi)^n}\]
在上式中取 \(\xi(t)=x-t\) ,得到以下推论:
推论: (柯西余项公式)\(\boxed{r_n(x_0;x)=\dfrac{1}{n!}f^{(n+1)}(\varepsilon)(x-\varepsilon)^n(x-x_0)}\)
取 \(\xi(t)=(x-t)^{n+1}\) ,就得到以下公式:
推论: (拉格朗日余项公式) \(\boxed{r_n(x_0;x)=\dfrac{1}{(n+1)!}f^{(n+1)}(\varepsilon)(x-x_0)^{n+1}}\)
泰勒级数展开
常见的麦克劳林级数
\(e^x=1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots+\dfrac{x^n}{n!}+\cdots\)
\(\ln(1+x)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\cdots+\dfrac{(-1)^{n-1}x^n}{n}+\cdots\)
\(\ln(1-x)=-x-\dfrac{x^2}{2}-\dfrac{x^3}{3}+\cdots\)
\(\dfrac{1}{1-x}=1+x+x^2+x^3+x^4+\cdots\)
\(\sin(x)=x-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dfrac{x^7}{7!}+\dfrac{x^9}{9!}-\cdots\) for all \(x\)
\(\cos(x)=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\cdots\) for all \(x\)
\(\sqrt{1+x}=1+\dfrac{1}{2}x-\dfrac{1}{8}x^2+\dfrac{1}{16}x^3+\dfrac{-5}{128}x^4+\dfrac{7}{256}x^5+\cdots\) }
示例: (2022.新高考 I)\(a=0.1e^{0.1},\ b=\dfrac{1}{9},\ c=-\ln0.9\) ,则
A. \(a<b<c\)B. \(c<b<a\)C. \(c<a<b\)D. \(a<c<b\)
解: (1) 先比较 \(a\) 和 \(b\) ,\(\ln(10a)=0.1\quad\ln(10b)=-\ln(1-0.1)\)
比较 \(x\) 与 \(-\ln(1-x)\) 的大小,这是很容易的 \(a<b\)
- 比较 \(b\) 和 \(c\) ,\(b=\dfrac{1}{9},\quad c=\ln(1+\dfrac{1}{9})\) ,
因为 \(x>\ln(1+x)\) 因此 \(b>c\)
- 比较 \(a\) 和 \(c\) 的大小,\(f(x)=xe^x+\ln(1-x)\)
\(f'(x)=(x+1)e^x-\dfrac{1}{1-x},\quad f'(0)=0\)
\(f''(x)=(x+2)e^x-\dfrac{1}{(1-x)^2},\quad x\in[0,0.1]\) 时 \(f''(x)>0\)
因此 \(f(0.1)>0\) 即 \(a>c\) 因此答案为 C 。☐
解: \(xe^x=x+\dfrac{x^2}{1!}+\dfrac{x^3}{2!}+\cdots\)\(0.1e^{0.1}=0.1+0.01+0.0005+\cdots\)
\(\dfrac{1}{9}=0.11111\cdots\)
\(-\ln(1-x)=x+\dfrac{x^2}{2}+\dfrac{x^3}{3}+\cdots\)\(-\ln(0.9)=0.1+0.005+\cdots\)
于是可知 \(0.1e^{0.1}<-ln(0.9)<\dfrac{1}{9}\)☐
示例: (2022.全国甲)已知 \(a=\dfrac{31}{32},b=\cos\dfrac{1}{4},c=4\sin\dfrac{1}{4}\),则
A. \(c>b>a\)B. \(b>a>c\)C. \(a>b>c\)D. \(a>c>b\)
解: (1) 先比较 \(a\) 与 \(b\) ,这里我们要挑一个多项式偶函数表示 \(\dfrac{31}{32}\)
第一项是 \(1\) ,这样和 \(\cos x\) 在 \((0,1)\) 相切,再凑二次项
令 \(a(x)=1-\dfrac{1}{2}x^2,\ b(x)=\cos x\), \(f(x)=1-\dfrac{x^2}{2}-\cos x\)
\(f(0)=0,\ f'(0)=0,\ f''(x)=-1+\cos x\leq0\)
因此 \(f(\dfrac{1}{4})<0\) 即 \(a<b\) 。
- 再比较 \(x=\dfrac{1}{4}\) 时 \(a(x)\) 与 \(c(x)=4\sin x\) 的大小。
这里我们要挑一个多项式奇函数表示 \(\dfrac{31}{32}\) 。
第一项是 \(4x\) ,因为这样和 \(4\sin x\) 在原点相切。
再凑余项,得到 \(a(x)=4x-2x^3\)
令 \(f(x)=a(x)-c(x)=4x-2x^3-4\sin x\)
\(f(0)=0,\ f'(0)=0,\ f''(x)=-12x+4\sin x\)
在 \(x>0\) 时 \(f''(x)<0\) ,从而 \(f(\dfrac{1}{4})<0\) ,即 \(a<c\)
- 最后比较 \(b\) 与 \(c\) 的大小
\(x\in(0,\dfrac{\pi}{2})\) 时 \(\tan x > x\) ,因此 \(\dfrac{c}{b}=4\tan\dfrac{1}{4}>1\),即 \(c>b\)
综上所述,本题选 A 。☐
解: 利用泰勒级数展开:
示例: (2021.全国乙卷)设 \(a=2\ln1.01,\ b=\ln1.02,\ c=\sqrt{1.04}-1\) ,则 \((\ \ \ \ )\)
A. \(a<b<c\)B. \(b<c<a\)C. \(b<a<c\)D. \(c<a<b\)
解: (1) \(a=\ln(1.01)^2>\ln1.02=b\) ,即 \(a>b\)
- 比较 \(a\) 与 \(c\) ,\(f(x)=a(x)-c(x)=2\ln(1+x)-\sqrt{1+4x}+1\)
\(f(0)=0,\ f'(x)=\dfrac{2}{1+x}-\dfrac{2}{\sqrt{1+4x}}\)
在 \(x\in[0,0.01]\) 区间考查 \(f'(x)\) 的正负性:不要一味二阶导数,能用代数法要想得起来用
\(x\in(0,0.01)\) 时,\(2x>x^2\) 所以 \((1+2x)^2<1+2x+x^2<1+4x\)
从而 \(f'(x)>0,\ x\in(0,0.01)\) ,得到 \(a>c\) 。因此本题选 B 。☐
示例: 已知 \(a=e^{0.05},\ b=\dfrac{\ln1.1}{2}+1,\ c=\sqrt{1.1}\) ,则 \((\ \ \ \ )\)
A. \(a>b>c\)B. \(c>b>a\)C. \(b>a>c\)D. \(a>c>b\)
示例: 设 \(a=e^{1.3}-2\sqrt{7},\ b=4\sqrt{1.1}-4,\ c=2\ln1.1\) ,则
A. \(a<b<c\)B. \(a<c<b\)C. \(b<a<c\)D. \(c<a<b\)