数据分析
导言
数据可视化,是将数据以表格或图的形式表示出来,能够直观地看出数据的特点,从而指导人们的实际活动。
下图 1 将某个英语培训机构的教师指导的学生人数(左)转化成了直观的数据图(右),哪位老师的学生多,哪位老师的学生少,是不是一目了然?

思考与讨论
- 上述图表有什么局限性?你能想到什么改进的方法?
示例: 在生产生活中产生的大量垃圾,正在严重侵蚀我们的生存环境,垃圾分类是实现 垃圾减量化、资源化和无害化的有效途径。2019年11月27日,北京市十五届人大常委会第16次会议表决通过北京市人大常委会关于修改《北京市生活垃圾管理条例》的决定,使得北京市的垃圾分类工作有法可依。图 2 显示了某个垃圾分类回收站下半年的旧报纸回收数据。请根据图中显示数据,计算报纸下半年报纸回收的总重量,并计算每月的平均回收量。

直方统计图
直方图(Histogram)
直方图是一种统计报告图,由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据的不同种类或数值,纵轴表示分布情况。
示例: 以下数据是某个班级期中考试的数学成绩,从这一堆数字中,你能看出什么有用的信息么?

将数据整理成直方图 3 后,你又能看出什么有用的信息?

在实践中为了方便进行统计工作,可以采用某种准备好的表格(图 4)来辅助图表的制作。

思考与讨论
- 根据上述图表,估计全班的数学平均成绩。
- 根据原始数据,用计算器计算全班的平均成绩。
- 你的估算接近计算结果么?如果相差较大,反思并改进你的估算方法。
- 上述制作方法还可以怎样改进?
示例: 图 5 给出了历任美国总统的寿命(乔治.华盛顿 至 罗纳德.里根),单纯罗列这些数字,我们很难看出有用的数据。
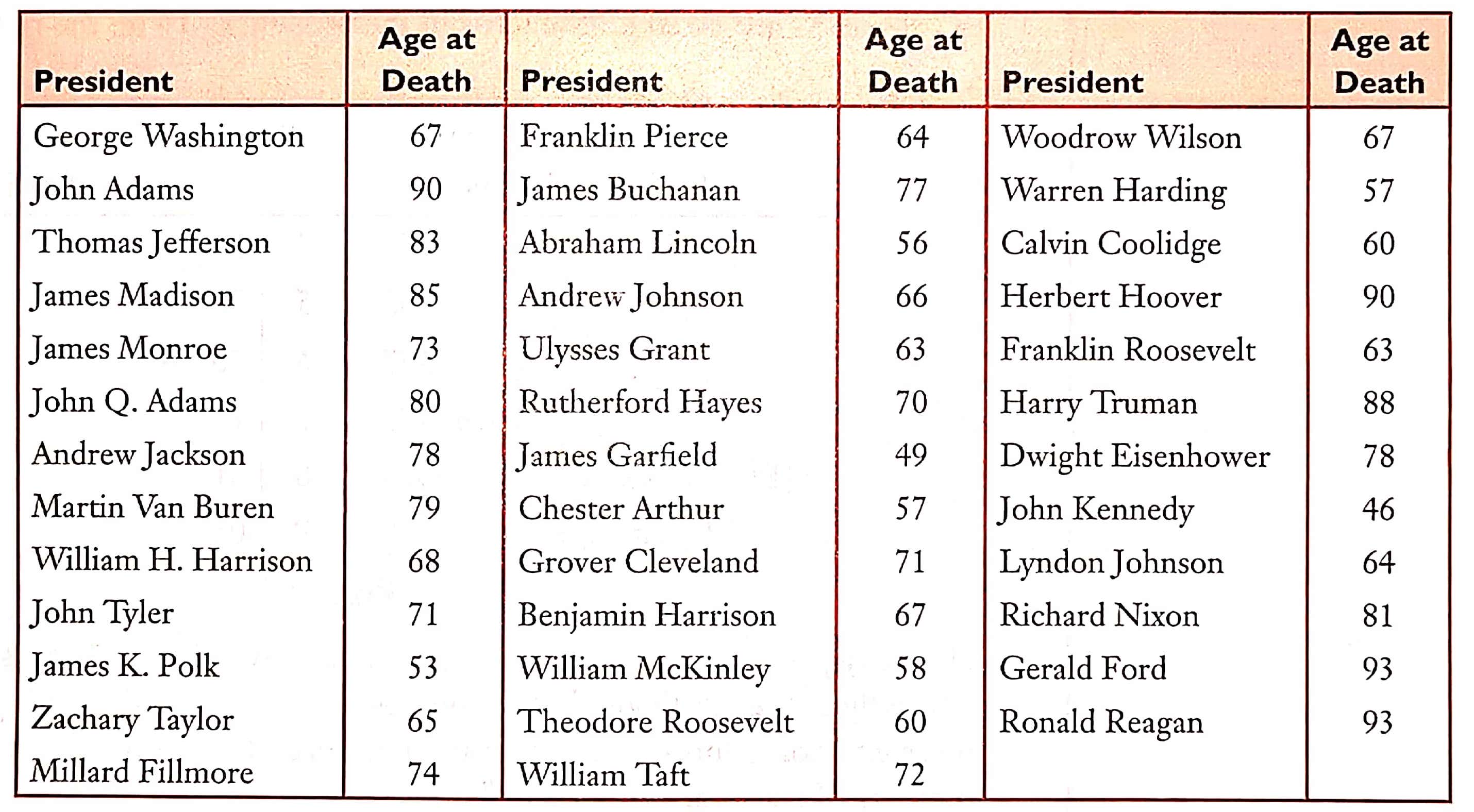
首先,请利用下面的方格阵列,使用前述方法整理数据:

思考与讨论
- 你能从上述图表中看出什么?
- 上述数据可视化方法有什么局限性?
- 你能想到什么改进的方法?
在绘制直方图时,往往将数据划分为不同的区间,针对每个区间统计数据样本出现的频度。例如上述数据按照 \(10\) 岁一组的年龄段可以整理为右图 6 所示表格。然后如图 所示,根据上述统计结果绘制柱状直方图 (a) 或茎叶图 (b) 。

提示:在汉字文化圈,“画正字”是一种非常方便的计数方式,你知道什么是“画正字”么?
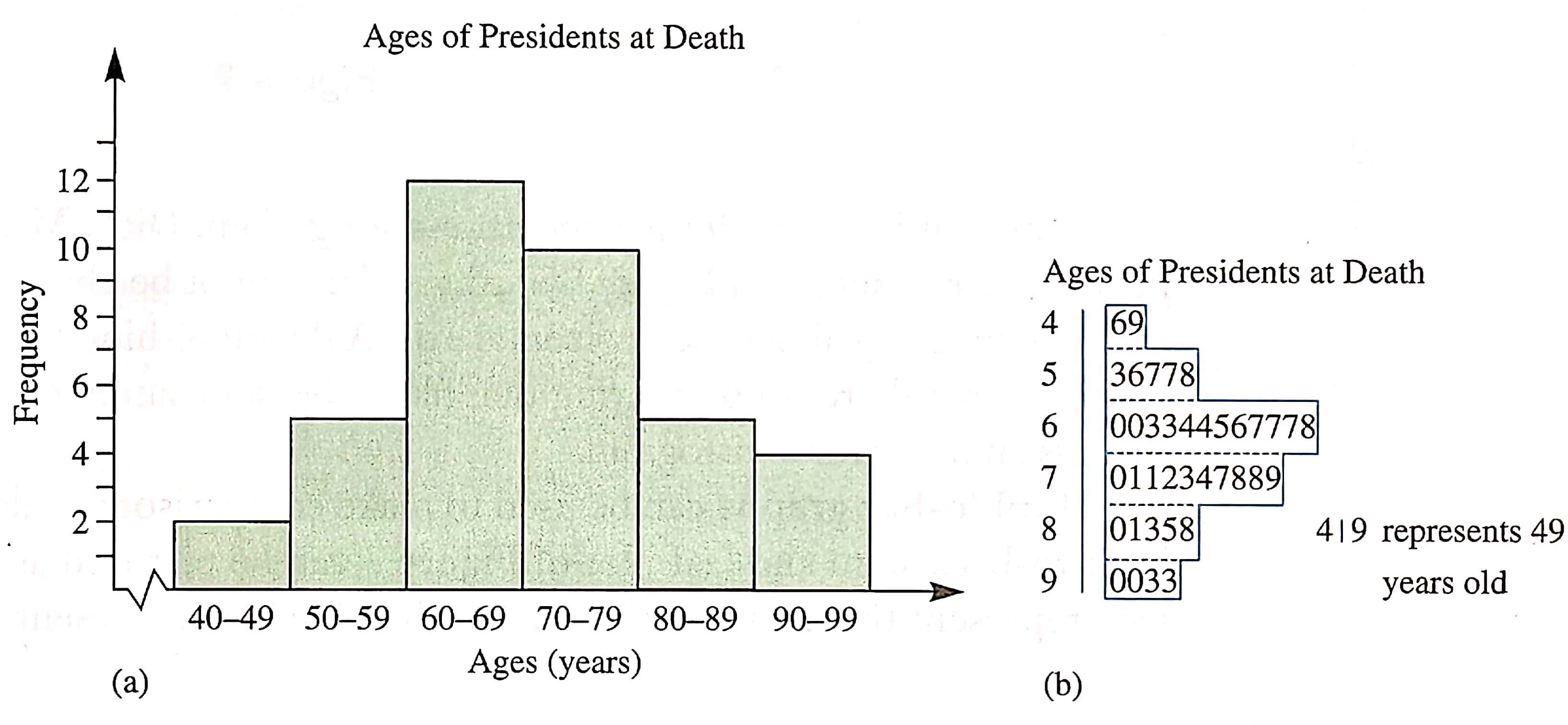
柱状直方图丢失了一些数据信息,即美国总统的寿命分布细节,但直观地表示出了寿命的大致分布。茎叶图则完整地保留了年龄的细节信息。茎叶图还可以用来比对两组不同的数据。例如在上述美国总统寿命数据中,可以将全部的总统按任职时间分为早期和晚期,将寿命数据绘制在茎叶图的两侧,如图 8所示。
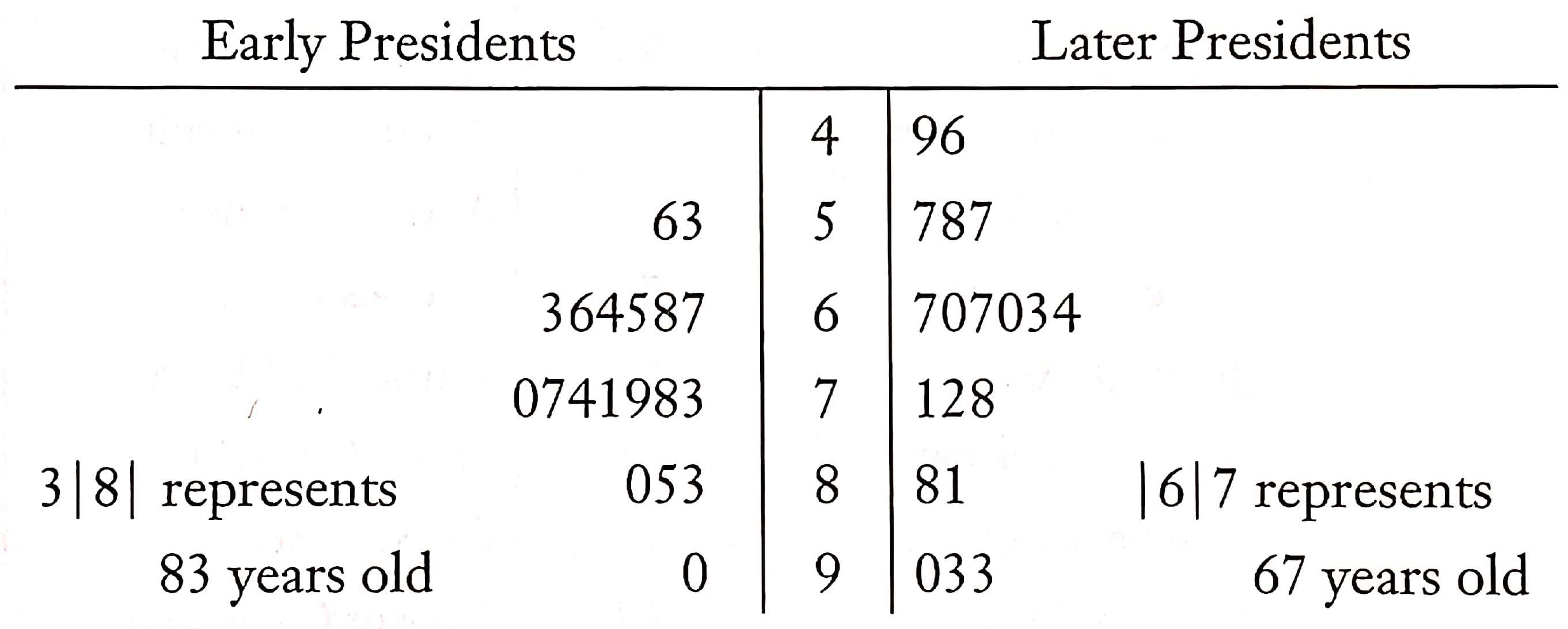
示例: 将前述示例的班级学生成绩,绘制成茎叶图。如果想对比第一行和第二行的成绩,茎叶图又应当如何绘制?(成绩重录如下)

百分比图
百分比图显示一个数据系列中各项的大小与各项总和的比例。
示例: 泰坦尼克号是当时世界上体积最庞大的客运轮船。然而不幸的是在首次航行即遭厄运。 1912年4月14日,泰坦尼克号与一座冰山相撞,次日泰坦尼克号沉入大西洋底。图 9 显示了头等舱、二等舱、三等舱和船员中的遇难与幸存者人数。
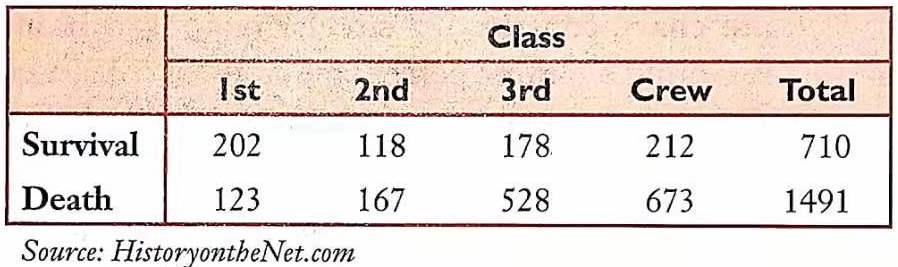
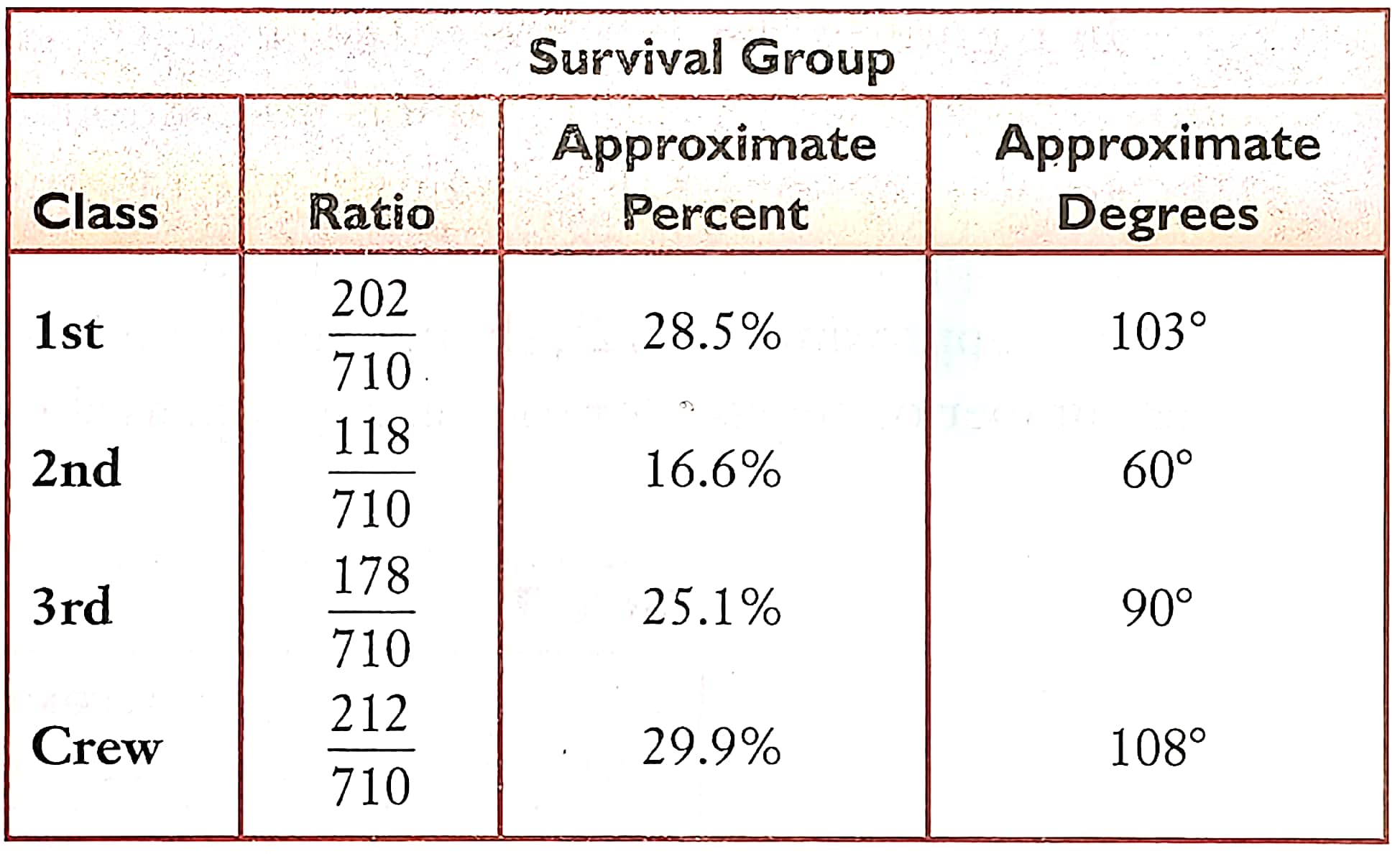
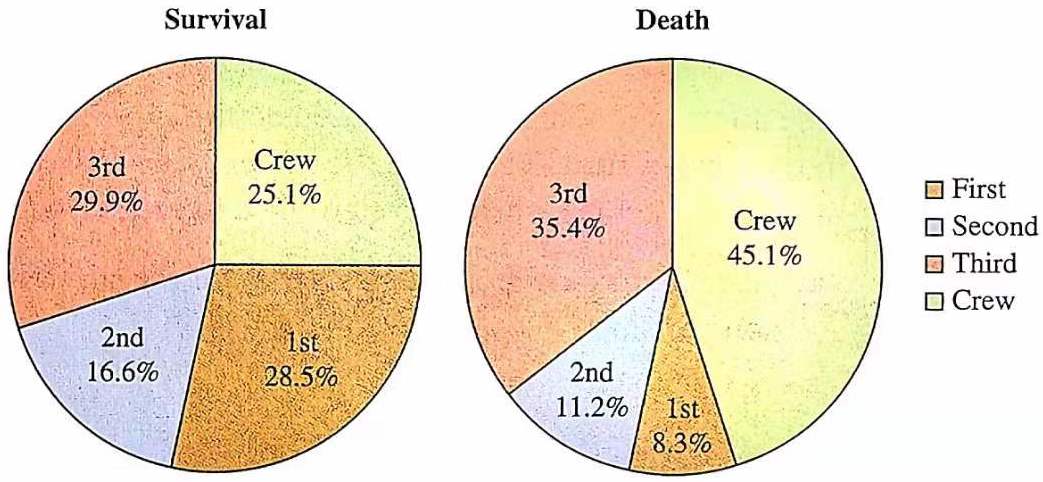
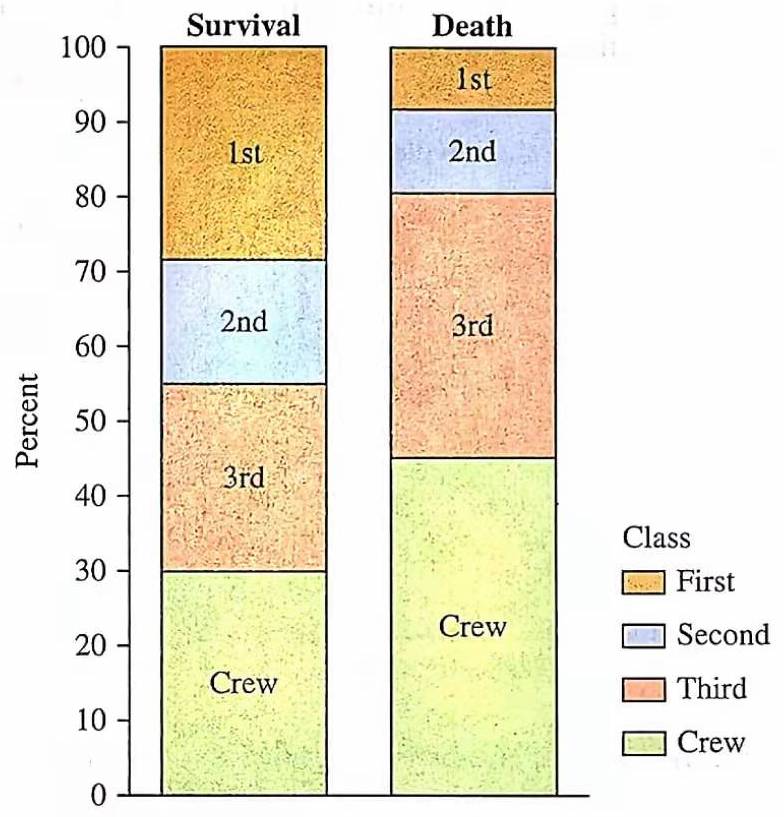
为了清晰地表现各类乘客在幸存者和遇难者中的比例,我们绘制百分比图。首先计算各类乘客占据的百分比,再换算成扇形的角度,如图 10 所示。最终绘制成饼图,并且为每种数据对应的扇形区域着不同的颜色,如图 (左)所示。另外,也可以使用柱状百分比图,如图 (右)所示。
折线图
折线图可以显示随时间或其它变量的变化而变化的连续数据,因此非常适用于显示在相等时间间隔下数据的趋势。
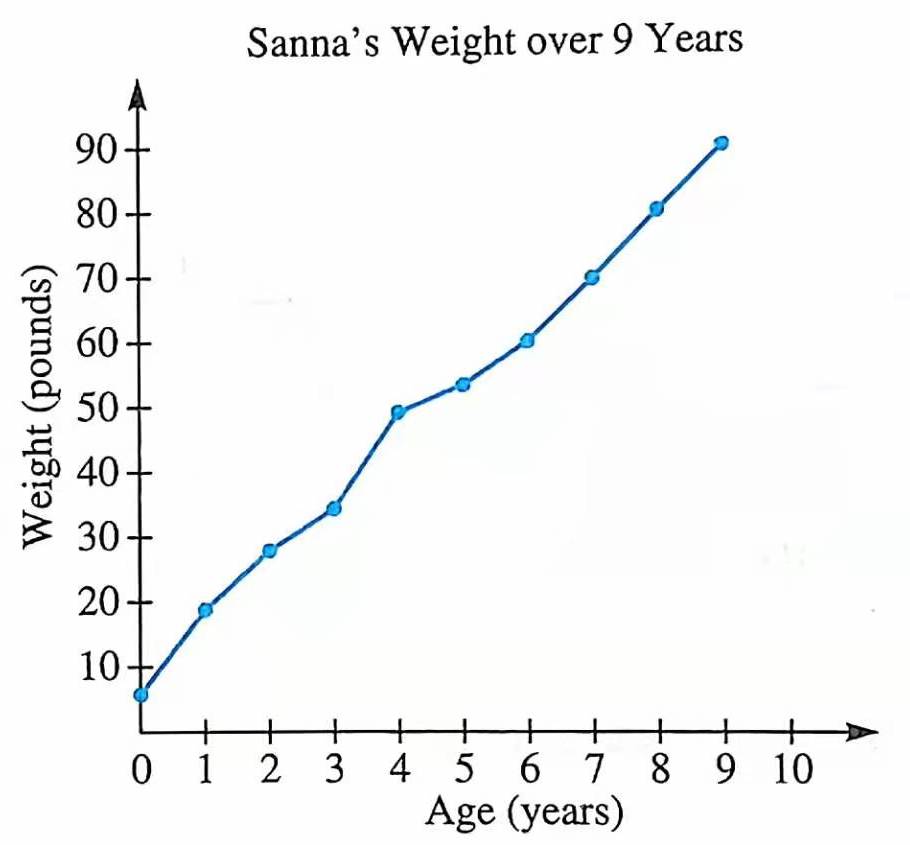
示例: 图 12 显示了 Sanna 的体重从出生开始到 \(9\) 岁的变化趋势图。从图中可以看出,这位小朋友的体重在 \(9\) 岁时达到了 \(90\) 磅(约合 \(40.8kg\))。体重增长最快的时间段是三到四岁之间。
示例: 如果某个量随另外一个量的均匀变化成等差数列,那么称这种关系为线性关系。例如一个首项为 \(2\) 公差为 \(2\) 的等差数列:\[2,4,6,8,10,12,14,16,18,20,...\]
下图 13 将该等差数列的前 \(10\) 项标记在坐标格中,每个点代表(项,项数)的关系:
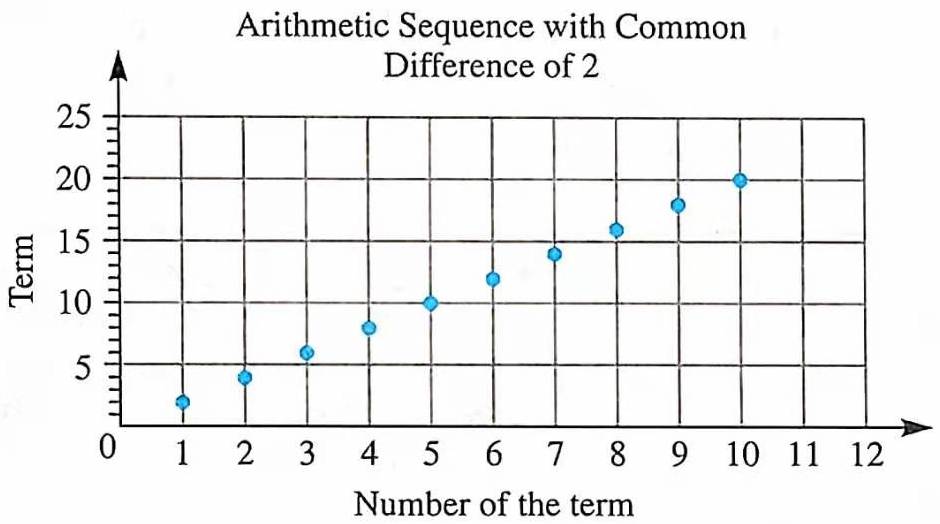
可以看到这些点都在一条直线上,如下图 14 所示:
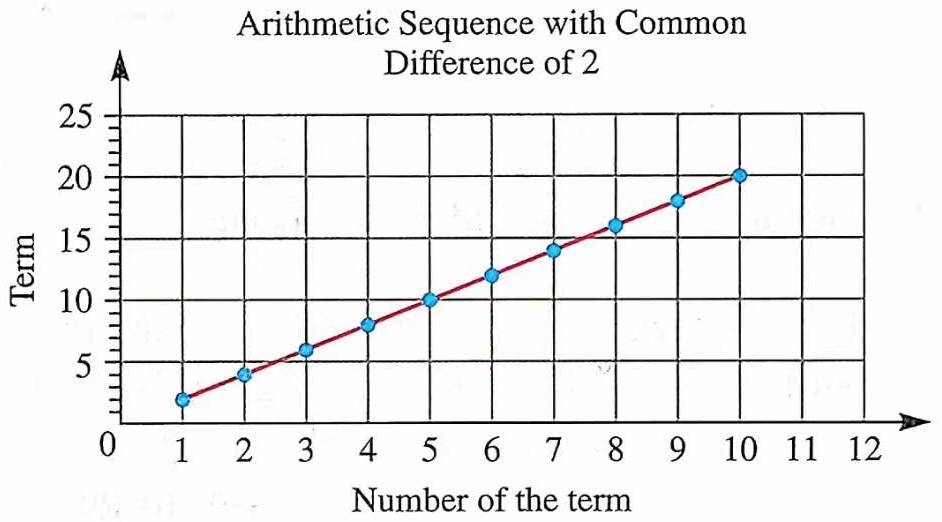
实践中,数据之间往往不是严格成线性关系,甚至影响因素很多,但我们往往首先致力于从数据中找出某种“线性关系”。
示例: 图 15 (a) 展示了某班级学生的学习时间和测验成绩的统计数据。从数据中可以看出(图 (b)),大体上,在一个时间范围内的学习时间越长,成绩越好,但也不尽然。
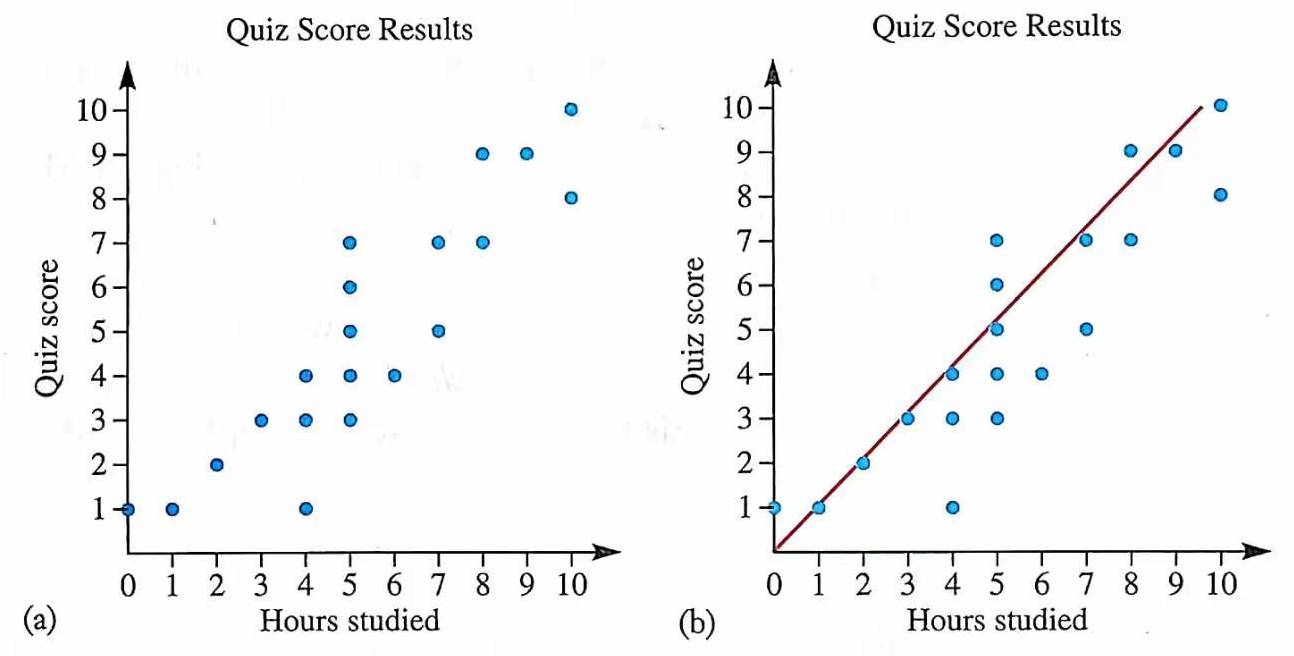
示例: 多折线图能够方便地对比几组数据的不同趋势,下表给出了美国五个州在上世纪的人口增长趋势,图 17 将数据绘制为多折线图。从折线图可以看出,佛罗里达州的人口增长速度远远超过其它四个州。

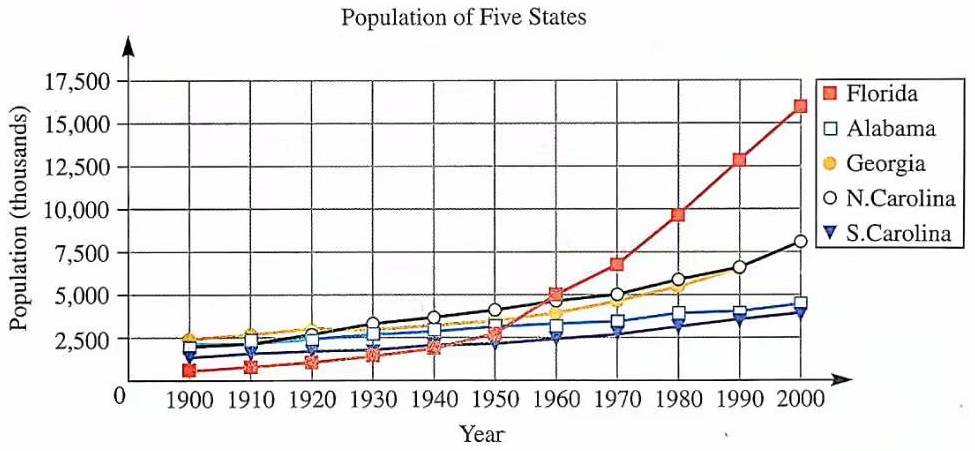
平均数
如果想用一个数表示一组数据的特征,你往往应当采用平均数。虽然这样处理会“丢失掉”很多信息,但平均数仍然是人们首先要考虑的指标。
示例: 图 18 展示了统计数据的平均数。这三组数据的平均数都是 \(5\) ,你能从图中读出这两组数据么,这两组数据有什么不同?
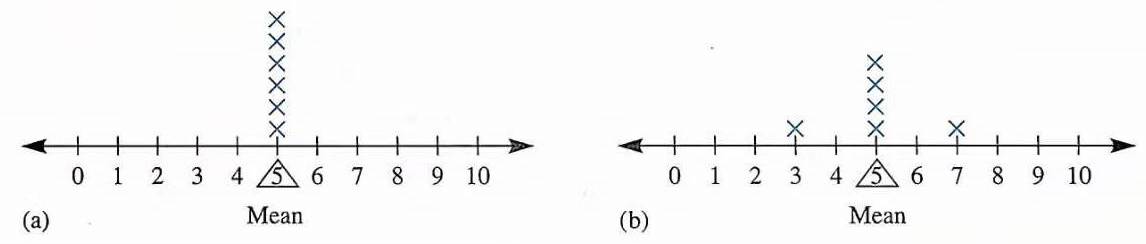
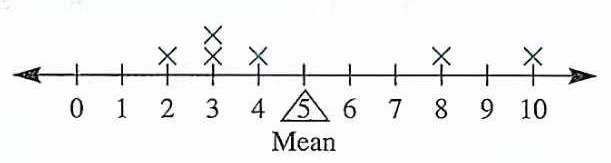
思考与讨论
- 在计算一组数据的平均数时,有一个数据发生了变化,会对平均数产生什么影响?
- 上述数据虽然平均数相同,但还是有较大差别,这三组数据给你的感觉有什么不一样?
- 你能想出某种可以计算的指标,以具体计算结果的形式(一个数),表示这种给你的“不一样的感觉”么?
- 如果在测量时(比如测量身高),某次测量结果特别大或者特别小,应当如何计算平均数?
- 如果数据中有一小部分数据特别大,会对平均数产生什么影响,这时候还有什么方法表示数据的整体平均情况?
综合练习
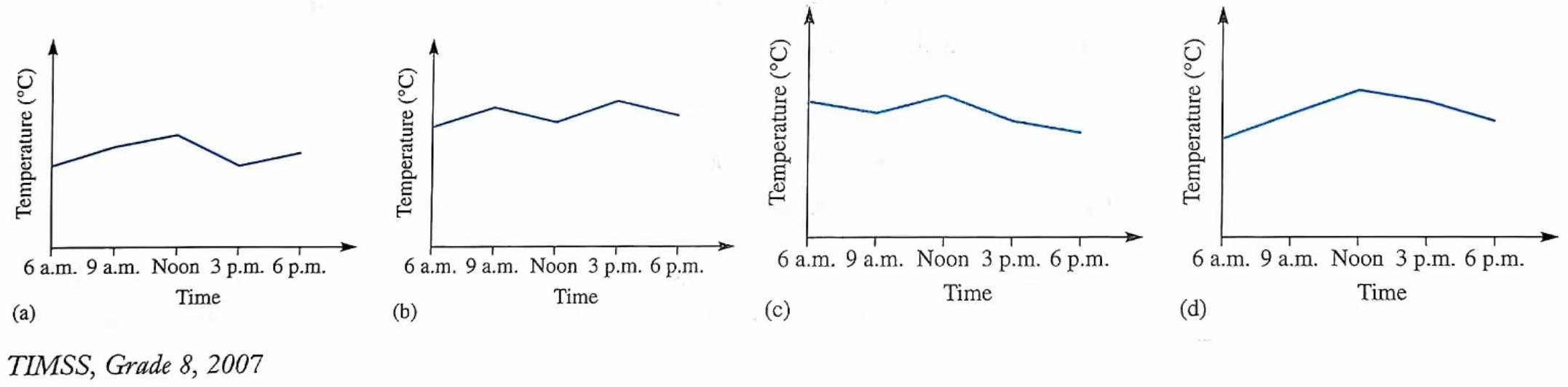
练习: 图 19 给出了某日的气温数据,图 中的四幅折线图,哪个能与该数据对应?请说明你的理由。

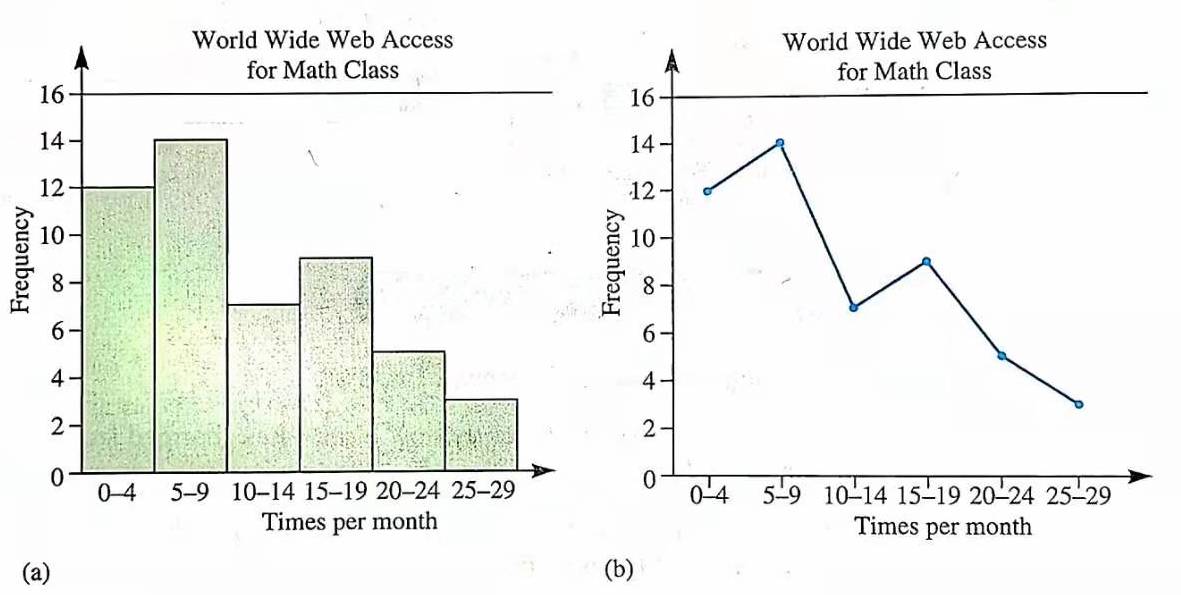
练习: 图 21 是某个数学网课在单月内的在线访问量统计柱状图和折线图,哪幅图更适合?请说明你的理由。
练习: 图 22 是 Abel 班里同学们最喜爱颜色的人数统计,哪幅图更适合?请说明你的理由。

练习: 右图 23 给出了某班级期中数学考试的成绩。
- 用计算器计算平均分。
- 自定分数段,绘制柱状统计图。
- 绘制茎叶图。

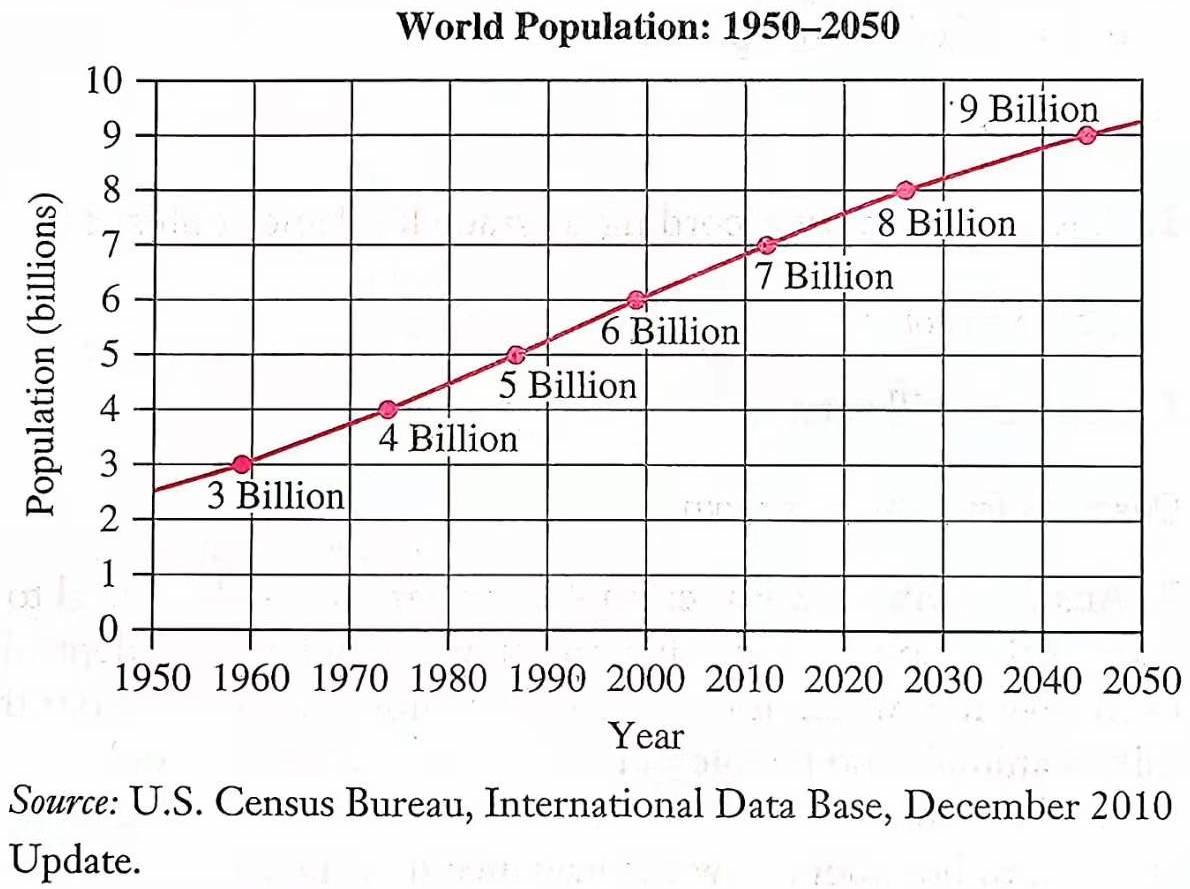
练习: 图 24 是 1950 年到 2050 年的世界人口趋势统计和预测图。图中的 Billion 代表十亿。根据该图回答以下问题:
- 1970 年时世界人口约为多少?
- 上世纪最后五十年,全球平均每年增长的人口数大约是多少?
- 这张图是 2010 年绘制的,本讲义写作时已经是 2021 年了,上网查一查资料,图中对全球 2020 年人口的预测准么?
练习: 图 25 是某商店在 2010 年和 2011 年的雪铲销售数量统计图。根据该图回答问题:
- 雪铲的销售主要集中在哪几个月,为什么?
- 对比 2010 年和 2011 年的销售情况的差别,并猜测导致这种差别的原因。

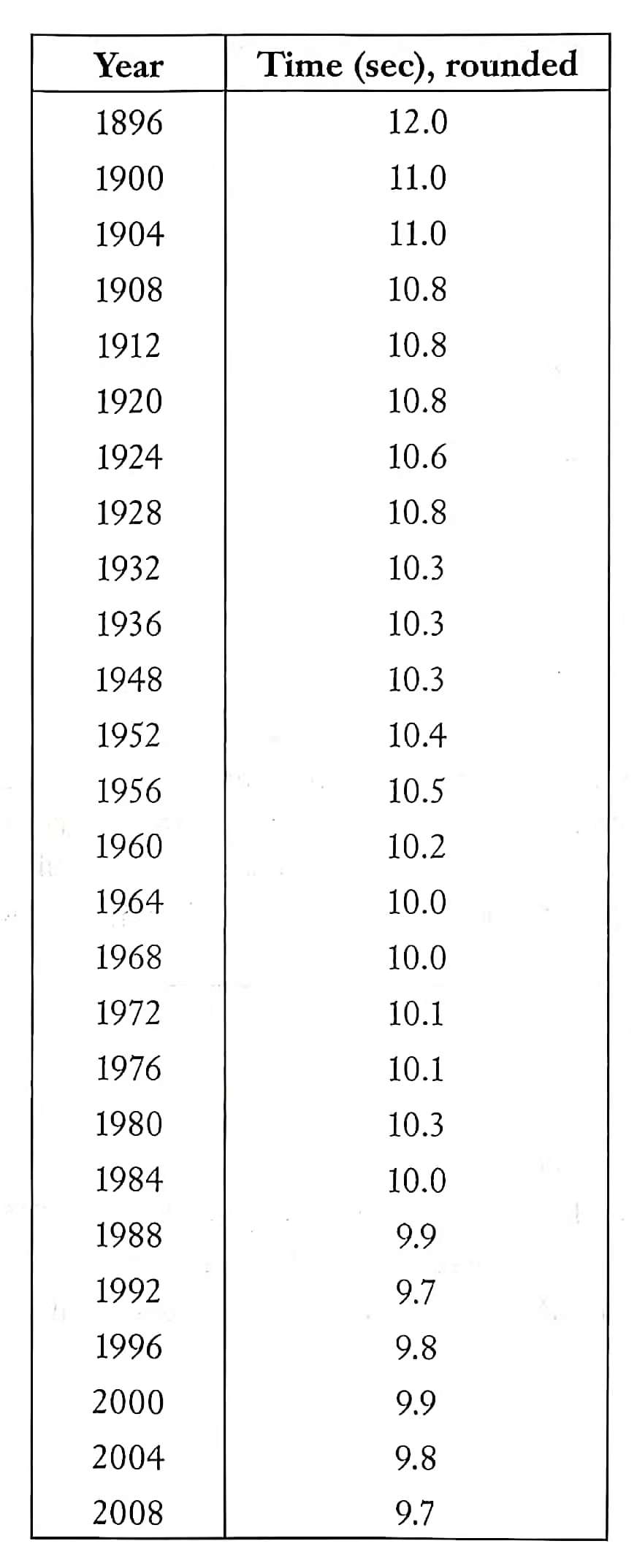
练习: 右图 26 给出了历届奥运会的男子百米赛跑夺冠成绩,请自选两种恰当的数据可视化方案,说明选择依据,绘制数据统计图。
练习: 两个数的平均数是 \(10\) ,其中一个数增加 \(6\) ,平均数变为多少?
练习: 两个数的平均数是 \(10\) ,其中一个数增加一定数值,导致平均数增加 \(6\) 。请问该数增加了多少?
练习: 一共有三个数,其中前两个数的平均数是 \(10\) ,第三个数比前两个数的平均数大 \(6\) 。请问这三个数的平均数是多少?
练习: 四(1)班同学参加数学竞赛,全班同学的平均分是 \(90\) 分,男生的平均分是 \(88\) 分,女生的平均分是 \(93\) 分。女生有 \(18\) 人,男生有多少人?
练习: 小明测试每分钟跳绳的数量,前四次跳绳的数量分别是 \(180\) 下、\(180\) 下、\(175\) 下和 \(185\) 下,第五次跳绳的数量比这五次跳绳的平均数量多 \(32\) 下,那么这五次跳绳的平均数是多少下?第五次跳了多少下?
练习: 王华期中考试数学、语文、英语三科的平均分是 \(98\) 分,其中语文 \(94\) 分,数学和英语的分数相同。请问王华的数学和英语各得了多少分?
练习: 王红期末考试语文、英语两科的平均成绩是 \(94\) 分,数学、英语两科的平均成绩是 \(96\) 分,语文数学两科的平均成绩是 \(98\) 分。请问王红这三科的成绩分别是多少?
练习: 小刚所在班级的六名学生(不包括小刚)在体育课上 1 分钟跳绳的平均成绩是 \(102\) 下,小刚 \(1\) 分钟跳了 \(130\) 下。请问总共七名同学的平均成绩是多少?
练习: “航海”号渔船出海捕鱼。上半月出海 \(12\) 天,共捕鱼 \(599\) 吨,下半月出海 \(13\) 天,平均每天捕鱼 \(52\) 吨。请问“航海”号渔船这个月在出海的日子里平均每天捕鱼多少吨?