圆锥曲线的计算技巧

二阶行列式

二阶行列式在很多情况下能够简化公式的表示，我们先给出二阶行列式的定义： \[\begin{equation*} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} \triangleq a_{11}a_{22}-a_{12}a_{21} \end{equation*}\]

示例：熟悉二阶行列式最简单的方法就是算一些行列式：

\[\begin{equation*} \begin{vmatrix} 1 & 2\\ 3 & 4 \end{vmatrix} = 1\times4-2\times3=-2 \end{equation*}\]

\[\begin{equation*} \begin{vmatrix} 2 & 3\\ -1 & 4 \end{vmatrix} = 2\times4-3\times(-1)=11 \end{equation*}\]

☐

示例：交换二阶行列式的行或者列，行列式会变为相反数：

\[\begin{equation*} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22}-a_{12}a_{21} \end{equation*}\]

\[\begin{equation*} \begin{vmatrix} a_{12} & a_{11}\\ a_{22} & a_{21} \end{vmatrix} = a_{12}a_{21}-a_{11}a_{22} \end{equation*}\]

☐

示例：沿主对角线翻转二阶行列式，其值不变：

\[\begin{equation*} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} = \begin{vmatrix} a_{11} & a_{21}\\ a_{12} & a_{22} \end{vmatrix} \end{equation*}\]

示例：线性方程组的解可以写成行列式的表示：

对于二元一次线性方程组： \[\begin{equation*} \begin{cases} a_{11}x_1+a_{12}x_2=b_1\\ a_{21}x_1+a_{22}x_2=b_2 \end{cases} \end{equation*}\]

当且仅当其系数行列式非零时，方程组有且只有唯一解，即： \[\begin{equation*} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} \neq 0 \end{equation*}\]

方程组的解是： \[\begin{equation*} x_1=\dfrac{\begin{vmatrix} b_{1} & a_{12}\\ b_{2} & a_{22} \end{vmatrix}}{\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix}},\ \ x_2=\dfrac{\begin{vmatrix} a_{11} & b_{1}\\ a_{21} & b_{2} \end{vmatrix}}{\begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix}} \end{equation*}\]

如果系数行列式等于零，方程组有无穷多组解或无解。

☐

思考与讨论

当二元一次线性方程组的系数行列式等于零时，方程组有无穷多组解和无解的条件分别是什么？

求两条直线的交点

示例：（2023 北京.19）已知椭圆 \(E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) 的离心率为 \(\dfrac{\sqrt{5}}{3}\)，\(A,C\) 分别是圆的上下顶点，\(B,D\) 分别是圆的左右顶点。\(|AC|=4\) 。

[(1)] 求 \(E\) 的方程；
[(2)] 设 \(P\) 是 \(E\) 在第一象限上的动点，直线 \(PD\) 与直线 \(BC\) 于点 \(M\) ，直线 \(PA\) 与直线 \(y=-2\) 交于点 \(N\) 。求证：\(MN\parallel CD\) 。

解： (1) 根据条件列出以下方程组：

\[\begin{equation*} \begin{cases} e=\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}\\ b=|AC|/2=4\\ a^2-c^2=b^2 \end{cases} \end{equation*}\]

解得：\(a^2=9, b^2=4\) 。因此椭圆 \(E\) 的方程为 \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\) 。

根据题意画图，并设 \(P(m,n)\) ：

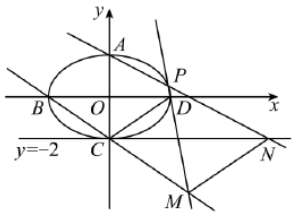
求 \(N\) 的坐标：\(\overrightarrow{AP}=(m,n-2)\), \(l_{AP}:(n-2)x-my=-2m\)

令 \(y=-2\) 得到 \(x=\dfrac{-4m}{n-2}\) ，即 \(N\left(\dfrac{-4m}{n-2}, -2\right)\)

求 \(M\) 的坐标：\(\overrightarrow{DP}=(m-3,n)\), \(l_{DP}:nx-(m-3)y=3n\)

\(\overrightarrow{BC}=(3,-2)\), \(l_{BC}:2x+3y=-6\) ，联立得

\[\begin{equation*} \begin{cases} nx-(m-3)y&=3n\\ 2x+3y&=-6 \end{cases} \end{equation*}\]

解得：提示

\(x=\dfrac{\begin{vmatrix} 3n & -(m-3)\\ -6 & 3 \end{vmatrix}}{\begin{vmatrix} n & -(m-3)\\ 2 & 3 \end{vmatrix}}=\dfrac{9n-6m+18}{3n+2m-6}\), \(y=\dfrac{-12n}{3n+2m-6}\)

即 \(M\left(\dfrac{9n-6m+18}{3n+2m-6}, \dfrac{-12n}{3n+2m-6}\right)\)

\(\overrightarrow{NM}=\left(\dfrac{9n-6m+18}{3n+2m-6}+\dfrac{4m}{n-2}, \dfrac{-12n}{3n+2m-6}+2\right)\)

\(\overrightarrow{NM}\cdot\overrightarrow{n_{cd}}=\begin{vmatrix} \dfrac{9n-6m+18}{3n+2m-6}+\dfrac{4m}{n-2} & 3\\ \dfrac{-12n}{3n+2m-6}+2 & 2 \end{vmatrix}\)

\(=2\cdot\left(\dfrac{9n-6m+18}{3n+2m-6}+\dfrac{4m}{n-2}\right)-3\cdot\left(\dfrac{-12n}{3n+2m-6}+2\right)\)

\(=\dfrac{18n-12m+36}{3n+2m-6}+\dfrac{8m}{n-2}+\dfrac{36n}{3n+2m-6}-6\)

\(=\dfrac{54n-12m+36}{3n+2m-6}-\dfrac{6n-8m-12}{n-2}\)

\(=\dfrac{4}{(3n+2m-6)(n-2)}\cdot(9n^2+4m^2-36)=0\)

故 \(MN//CD\) ，证毕。

☐

示例：

两点间距离公式

弦长公式

\(|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)

\(|AB|=\sqrt{1+k^2}\cdot|x_1-x_2|\)

\(|AB|=\sqrt{1+k^2}\cdot\sqrt{(x_1+x_2)^2-4x_1x_2}\)

\(|AB|=\sqrt{1+k^2}\cdot\dfrac{\sqrt{\Delta_x}}{|A_x|}\)

\(|AB|=|t_1-t_2|\)

示例：求 \(x^2+y^2=16\) 与 \(2x+y=2\) 相交弦的长度。

解：将方程连立：\(\begin{cases}x^2+y^2=16\\2x+y=2\end{cases}\)

消去 \(y\) 得到： \(x^2+(2-2x)^2=16\)

整理得到：\(5x^2-8x-12=0\)

\(L=\sqrt{5}\cdot\dfrac{\sqrt{304}}{5}\)

☐

圆的计算

弦长公式

圆的标准方程：\((x-a)^2+(y-b)^2=r^2\)

圆的一般方程：\(x^2+y^2+2Dx+2Ey+F=0\)

点 \((x_0,y_0)\) 和圆的位置关系：

\(\quad\) 点在圆外：\(x_0^2+y_0^2+2Dx_0+2Ey_0+F>0\)

\(\quad\) 点在圆上：\(x_0^2+y_0^2+2Dx_0+2Ey_0+F=0\)

\(\quad\) 点在圆内：\(x_0^2+y_0^2+2Dx_0+2Ey_0+F<0\)

过圆上一点 \((x_0,y_0)\) 做圆的切线：

\(\quad\) \(x_0x+y_0y=r^2\)

\(\quad\) \(x_0x+y_0y+D(x+x_0)+E(y+y_0)+F=0\)

简化计算的技巧

示例：联立 \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) 和 \(y=kx+m\) ，

求 \(\Delta\) ，\(x_1+x_2\)，\(x_1x_2\) 和 \(y_1+y_2\) 和 \(y_1y_2\) 的值。

解：联立消去 \(y\) 得到： \(\dfrac{x^2}{a^2}+\dfrac{(kx+m)^2}{b^2}=1\)

整理得到：\(\left(\dfrac{1}{a^2}+\dfrac{k^2}{b^2}\right)\cdot x^2+\dfrac{2km}{b^2}\cdot x+\dfrac{m^2}{b^2}-1=0\)

\(\Delta=\dfrac{4k^2m^2}{b^4}-4\cdot\left(\dfrac{1}{a^2}+\dfrac{k^2}{b^2}\right)\left(\dfrac{m^2}{b^2}-1\right)\)

你要记住这个结论

化简得：\(\Delta=4\cdot\left(\dfrac{1^2}{a^2}+\dfrac{k^2}{b^2}-\dfrac{m^2}{a^2b^2}\right)\qquad\bigstar\)

\(x_1+x_2=\dfrac{-\dfrac{2km}{b^2}}{\dfrac{1}{a^2}+\dfrac{k^2}{b^2}}\quad,\quad x_1x_2=\dfrac{\dfrac{m^2}{b^2}-1}{\dfrac{1}{a^2}+\dfrac{k^2}{b^2}}\qquad\bigstar\)

\(y_1+y_2=k(x_1+x_2+2m)=\dfrac{\dfrac{2m}{a^2}}{\dfrac{1}{a^2}+\dfrac{k^2}{b^2}}\)

\(y_1y_2=(kx_1+m)(kx_2+m)=\dfrac{\dfrac{m^2}{a^2}-k^2}{\dfrac{1}{a^2}+\dfrac{k^2}{b^2}}\)

☐

示例：根据上式结果，将表达式 \(x_1x_2+(y_1-1)(y_2-1)\) 展开。

解：原等式变形为：

\(x_1x_2+(kx_1+m-1)(kx_2+m-1)\)

\(=(1+k^2)x_1x_2+k(m-1)(x_1+x_2)+(m-1)^2\)

\(=(1+k^2)\cdot\dfrac{\dfrac{m^2}{b^2}-1}{\dfrac{1}{a^2}+\dfrac{k^2}{b^2}}+k(m-1)\cdot\dfrac{-\dfrac{2km}{b^2}}{\dfrac{1}{a^2}+\dfrac{k^2}{b^2}}+(m-1)^2\)

☐

齐次化联立

示例：已知椭圆 \(E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 (a>b>0)\) 的一个顶点为 \(A(0,1)\) ，焦距 \(2\sqrt{3}\)

[(1)] 求椭圆 \(E\) 的方程；
[(2)] 过点 \(P(-2,1)\) 作斜率为 \(k\) 的直线与椭圆交于不同的两点 \(B,C\) ，直线 \(AB,AC\) 分别与 \(x\) 轴交于点 \(M,N\) 。求 \(|MN|=2\) 时 \(k\) 的值。

解： (1) \(\dfrac{x^2}{4}+y^2=1\)

分析：将 \(A\) 平移至原点，则 \(|OM|,|ON|\) 与 \(k_{AB},k_{AC}\) 有简单的倒数关系，故可以尝试使用齐次化方法。题目描述的草图如下：

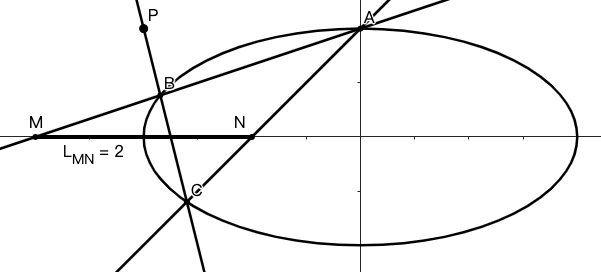
使用平移变换 \(\begin{cases}x=x'\\y=y'+1\end{cases}\)，该平移变换保持各直线斜率不变，同时将 \(A(0,1)\) 变换至 \(A'(0,0)\) ，\(P(-2,1)\) 变换至 \(P'(-2,0)\) 。将变换后的椭圆方程和过 \(P'\) 的直线联立：（其中直线采用截距式） \[\begin{cases} E':\dfrac{x'^2}{4}+(y'+1)^2=1\\l_{P'}:\dfrac{y'}{m}-\dfrac{x'}{2}=1 \end{cases}\]

\(B',C'\) 的横纵坐标满足上述方程，

进行齐次化处理得到： \(\dfrac{x'^2}{4}+y'^2+2y'\cdot(\dfrac{y'}{m}-\dfrac{x'}{2})=0\)

整理得到：\(\left(4+\dfrac{8}{m}\right)\left(\dfrac{y'}{x'}\right)^2-4\left(\dfrac{y'}{x'}\right)+1=0\)

\(k_{AB}\) 与 \(k_{AC}\) 为方程 \(\left(4+\dfrac{8}{m}\right)t^2-4t+1=0\) 的两根。

\(k_{AB}+k_{AC}=\dfrac{4}{4+8/m},\quad k_{AB}k_{AC}=\dfrac{1}{4+8/m}\)

\(|MN|=\left|\dfrac{1}{k_{AB}}-\dfrac{1}{k_{AC}}\right|=\dfrac{\sqrt{(k_{AB}+k_{AC})^2-4k_{AB}k_{AC}}}{k_{AB}k_{AC}}=\sqrt{\dfrac{-32}{m}}=2\)

得到 \(m=-8\) ，即过 \(P\) 的直线斜率为 \(k=-4\) 。

☐

示例：已知椭圆 \(E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 (a>b>0)\) 过点 \(A(0,-2)\) ，以四个顶点围成的四边形面积为 \(4\sqrt{5}\)

[(1)] 求椭圆 \(E\) 的标准方程；
[(2)] 过点 \(P(0,-3)\) 的直线 \(l\) 斜率为 \(k\) ，交椭圆 \(E\) 于不同的两点 \(B,C\)，直线 \(AB,AC\) 交于 \(y=-3\) 于点 \(M,N\) ，若 \(|PM|+|PN|\leq15\) ，求 \(k\) 的取值范围。

解： (1) \(\dfrac{x^2}{5}+\dfrac{y^2}{4}=1\)

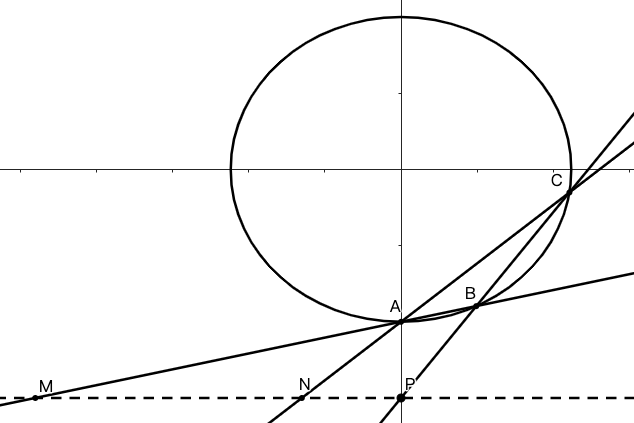
利用坐标平移变换 \(\begin{cases}x=x'\\y=y'-2\end{cases}\) 保持直线斜率不变，同时将 \(A\) 平移至 \(A'(0,0)\) ，\(P\) 平移至 \(P'(-1,0)\) 联立椭圆和过 \(P\) 的直线 \(l_{P'}\)

\(\begin{cases} E':\dfrac{x'^2}{5}+\dfrac{y'-2}{4}=1\\l_{P'}:kx'-y'=1 \end{cases}\Rightarrow25y'^2-20mx'y'+4x^2=0\)

\(B,C\) 两点的坐标满足方程： \(25\left(\dfrac{y'}{x'}\right)^2-20k\left(\dfrac{y'}{x'}\right)+4=0\)

\(k_{AB}+k_{AC}\) 是方程 \(25t^2-20k\cdot t+4=0\) 的两根。

由于 \(B,C\) 是不同的两点，\(\Delta=400(k^2-1)>0\) ，得到 \(|k|>1\) 。

于是 \(k_{AB}+k_{AC}=\dfrac{4k}{5},\quad k_{AB}+k_{AC}=\dfrac{4}{25}\)

\(M,N\) 在 \(y\) 轴同侧

\(|PM|+|PN|= \left|-\dfrac{1}{k_{AB}}\right|+\left|-\dfrac{1}{k_{AC}}\right|=\left|\dfrac{k_{AB}+k_{AC}}{k_{AB}k_{AC}}\right|=5|k|\leq15\)

得到 \(|k|\leq3\) ，综上所述 \(k\in[-3,-1)\cup(1,3]\)

☐