圆锥曲线
抛物线
抛物线的定义
定义: 抛物线是到某定点的距离等于到某不经过该点的定直线的距离的点的轨迹。该定点叫做焦点,该定直线叫做准线。
轴:抛物线是轴对称图形,它的对称轴简称轴。
顶点:抛物线与它的轴的交点叫做抛物线的顶点。
弦:抛物线的弦是连接抛物线上任意两点的线段。
焦弦:抛物线的焦弦是经过抛物线焦点的弦。
正焦弦:抛物线的正焦弦是垂直于轴的焦弦。
直径:抛物线的直径是抛物线一组平行弦中点的轨迹。这条直径也叫这组平行弦的共轭直径。
主要直径:抛物线的主要直径是抛物线的轴。
示例: 若动圆与一条已知直线相切,并且通过一个已知点,圆心的轨迹是什么?若动圆与一定圆和一定直线同时相切,圆心的轨迹又是什么?
示例: 在平面直角坐标系中,准线为 \(x=-\dfrac{p}{2}\) ,焦点为 \(F\left(\dfrac{p}{2},0\right)\) ,求抛物线的方程。
解: 设抛物线上点的坐标为 \((x,y)\) ,其到准线的距离为 \(\left|x+\dfrac{p}{2}\right|\) ,到焦点的距离为 \(\sqrt{\left(x-\dfrac{p}{2}\right)^2+y^2}\) ,根据抛物线定义得到:
\[\left(x+\dfrac{p}{2}\right)^2=\left(x-\dfrac{p}{2}\right)^2+y^2\]
整理得:\(y^2=2px\)☐
抛物线的标准方程
抛物线有四个标准方程,对于 \(p>0\) ( \(p\) 为焦准距):
\(y^2=2px\) 开口向右;
\(y^2=-2px\) 开口向左;
\(x^2=2py\) 开口向上;
\(x^2=-2py\) 开口向下;
抛物线的弦
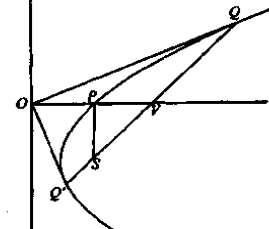
示例: 若抛物线的弦 \(P_1P_2\) 延长后交准线于 \(N\) , \(S\) 为抛物线焦点,求证 \(SN\) 平分 \(SP_1\) 与 \(SP_2\) 夹角的外角。

证法一设出弦端点的坐标,求各线段斜率,利用两角和正切计算:(笔记中 \(K\) 为 \(N\) 点)

至此经过简单比较可得 \(\tan2\theta=\tan(\alpha+\beta)\) ,再结合 \(N\) 在 \(P_1P_2\) 延长线上,得出外角平分线结论。
证法二 作 \(P_1,P_2\) 到准线的距离线段 \(P_1Q_1,P_2Q_2\) ,
利用 \(\triangle{NP_1Q_1}\sim\triangle{NP_2Q_2}\) 及抛物线的定义得到 \[\dfrac{NP_1}{NP_2}=\dfrac{P_1Q_1}{P_2Q_2}=\dfrac{SP_1}{SP_2}\]
再通过外角平分线定理即可得证。☐
示例: 设 \(P_1P_2\) 是抛物线的一条焦点弦,\(Q\) 是抛物线上另一点,若 \(P_1Q,P_2Q\) 分别交准线于 \(N_1,N_2\) , \(S\) 为抛物线焦点,求证: \(\angle{N_1SN_2}\) 是直角。
证法一 两次运用外角平分线结论即可。
证法二 与准线的两个焦点为 \(N_1,N_2\) 其纵坐标为弦端点纵坐标 \(y_1,y_2\) 的函数。在计算 \(\overrightarrow{SN_1}\cdot\overrightarrow{SN_2}\) 时,\(y_1,y_2\) 是对称的,故可以使用联立体系配合韦达定理求解。过程如下:
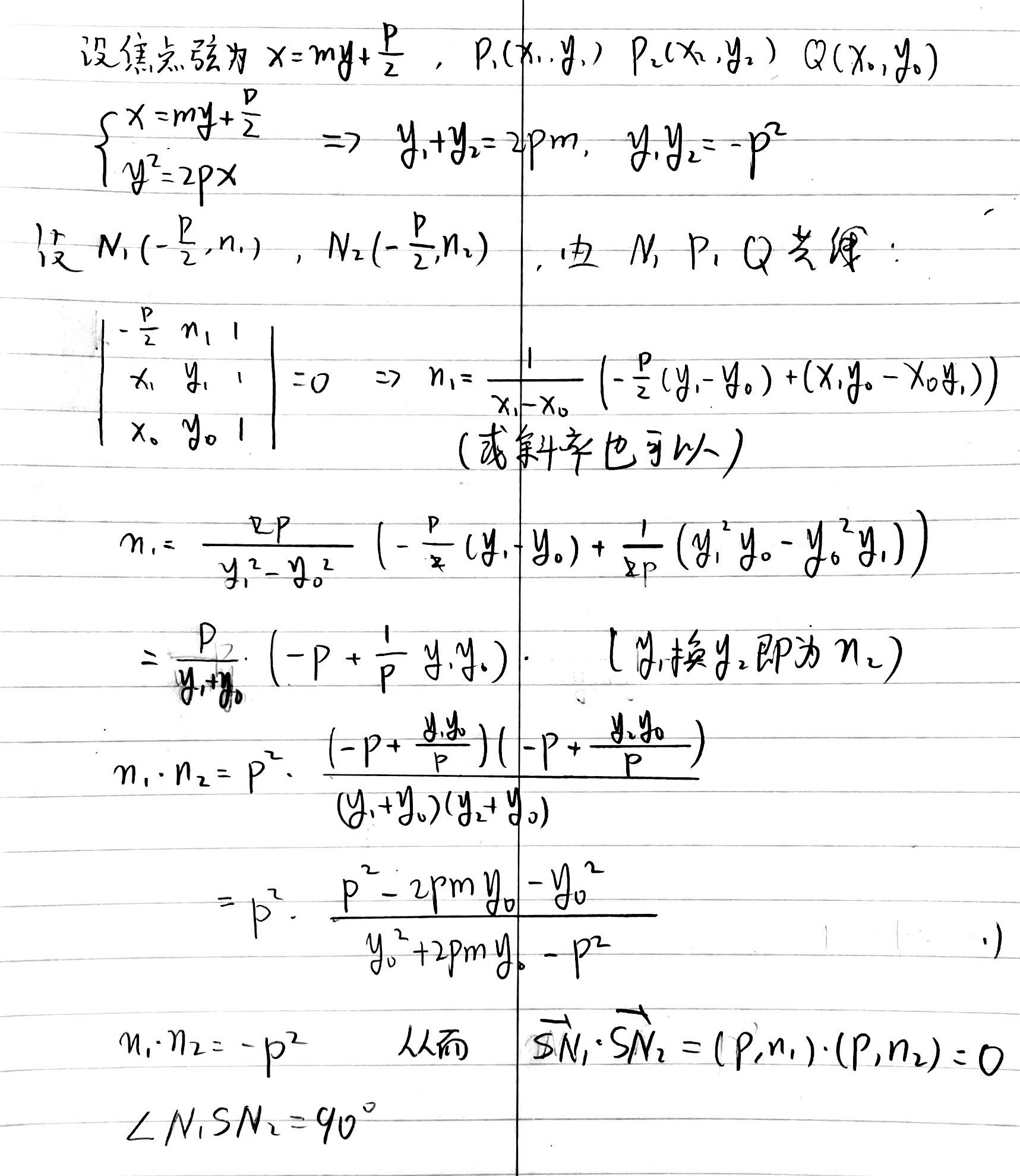
☐
示例: 设 \(P_1P_2,Q_1Q_2\) 是抛物线的焦点弦,抛物线焦点为 \(S\) 。求证:\(P_1Q_1\) 与 \(P_2Q_2\) 的交点 \(N_1\) 位于准线上, \(P_1Q_2\) 与 \(P_2Q_1\) 的交点 \(N_2\) 也位于准线上,且 \(\angle{N_1SN_2}=90^\circ\) 。
提示 作 \(\angle{P_1SQ_2}\) 的角平分线,角平分线的与 \(P_1Q_1\) 的交点在准线上,角平分线与 \(P_2Q_2\) 的交点也在准线上。故 \(P_1Q_1\) 与 \(P_2Q_2\) 的交点在准线上。类似地,\(\angle{P_1SQ_1}\) 的角平分线也有类似结论。
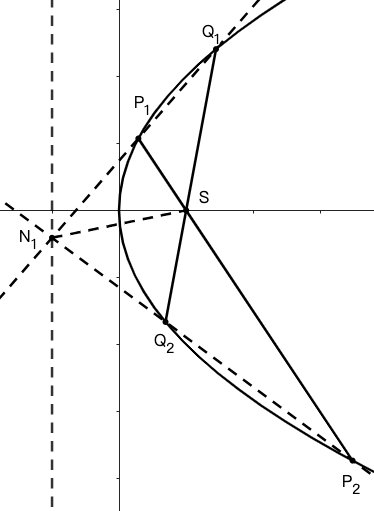
☐
示例: 设 \(P\) 是抛物线上任意一点,抛物线顶点为 \(A\) ,焦点为 \(S\) 。若 \(PA\) 延长后交准线于 \(K\) , \(P\) 在准线上的投影为点 \(M\) ,求证 \(\angle{MSK}\) 为直角。

提示 等腰加外角平分线。
示例: 设 \(PQ\) 是抛物线的双纵标线(垂直于轴的弦),抛物线顶点为 \(X\) ,\(PX\) 交曲线于 \(P'\) ,求证 \(P'Q\) 过抛物线的焦点。
提示 证明对顶角相等,从而说明 \(P'S\) 与 \(SQ\) 是一直线。
抛物线的纵标线
示例: \(P\) 为抛物线上一点,\(N\) 为 \(P\) 在轴上的投影。抛物线顶点为 \(A\) ,焦点为 \(S\) 。求证:\(PN^2=4AS\cdot AN\)\(\bigstar\) 此即为抛物线方程 \(y^2=2px\) 的推导
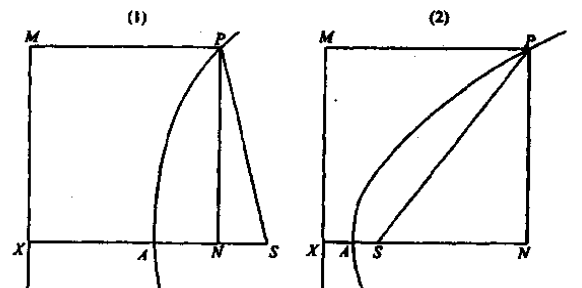
解: 为方便表示,设抛物线的焦准距为 \(p\) , \(AN=x\) 。
图 (1):\(NS=AS-AN=\dfrac{p}{2}-x\)
\(PS=MP=XN=XA+AN=\dfrac{p}{2}+x\)
\(PN^2=PS^2-NS^2=2px=4AS\cdot AN\)
图 (2):\(NS=AS-AN=x-\dfrac{p}{2},\ PS=\dfrac{p}{2}+x\)
同样可得:\(PN^2=PS^2-NS^2=2px=4AS\cdot AN\)☐
示例: 求证抛物线的正焦弦(垂直于轴的焦点弦)等于两倍的焦准距。
示例: 求证抛物线的正焦弦和顶点张成三角形的外接圆的半径等于正焦弦长的 \(\dfrac{5}{8}\)
示例: 设 \(P_1P_2\) 是抛物线的双纵标线,抛物线顶点为 \(A\) ,若 \(\triangle{P_1P_2A}\) 的外接圆与抛物线的轴交于另一点 \(Q\) ,\(P\) 在轴上的投影为 \(N\) ,证明 \(NQ\) 为定长。
示例: 设 \(P_1P_2\) 是抛物线的双纵标线,\(P_1P_2\) 与轴交于点 \(N\) 。又设 \(Q\) 为抛物线上另一点,过 \(Q\) 作两条直线,一条通过顶点,另一条平行于轴,分别交 \(P_1P_2\) 于 \(L_1,L_2\)。 求证:\(NL_1\cdot NL_2=PN^2\) 。
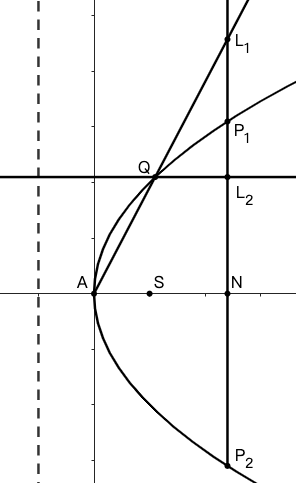
抛物线的切线
示例: 抛物线在点 \(P\) 的切线交准线于 \(Z\) ,焦点是 \(Z\) ,\(P\) 在准线的投影为 \(M\) 。那么 \(\angle{PSZ}\) 是直角,且 \(PZ\) 平分 \(\angle{SPM}\) 。

证法一 设抛物线的方程为 \(y^2=2px\) ,\(P(x_0,y_0)\) 。
方程两边对 \(x\) 求导得到:\(2yy'=2p\) 即 \(y'=\dfrac{p}{y}\)
从而得到 \(P\) 处切线斜率为 \(k_p=\dfrac{p}{y_0}\) 。
点 \(Z\) 的纵坐标为 \(y_z\) ,\(\dfrac{y_0-y_z}{x_0+\dfrac{p}{2}}=\dfrac{p}{y_0}\) ,得到 \(y_z=\dfrac{y_0}{2}-\dfrac{p^2}{2y_0}\)
\(\overrightarrow{ZS}=\left(p,-\dfrac{y_0}{2}+\dfrac{p^2}{2y^0}\right), \overrightarrow{SP}=\left(\dfrac{y_0^2}{2p}-\dfrac{p}{2},y_0\right)\),\(\overrightarrow{ZS}\cdot\overrightarrow{SP}=0\) ,因此 \(\angle{PSZ}=90^\circ\bigstar\)
设 \(PZ\) 倾斜角为 \(\theta=\angle{MPZ}\) ,则
\(\tan2\theta=\dfrac{2k_p}{1-k_p^2}=\dfrac{2\cdot\dfrac{p}{y_0}}{1-\left(\dfrac{p}{y_0}\right)^2}=\dfrac{2y_0p}{y_0^2-p^2}\)
\(k_{PS}=\tan{\angle{MPS}}=\dfrac{y_0-0}{x_0-\dfrac{p}{2}}=\dfrac{y_0}{\dfrac{y_0^2}{2p}-\dfrac{p}{2}}=\dfrac{2y_0p}{y_0^2-p^2}\)
结合图像及 \(\theta\) 范围,可判断 \(PZ\) 平分 \(\angle{MPS}\) 而非外角。☐
证法二 如图 9 作弦 \(PP'\) , \(ZS\) 平分 \(\angle{PSP'}\) 的外角。
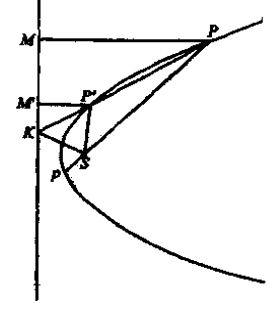
根据切线的定义 \(PZ\) 当 \(P'\) 无限接近于 \(P\) 时,\(PP'\) 即为切线 \(PZ\)
因此 \(ZS\) 平分 \(\angle{PSP'}=0^\circ\) 的外角,即 \(\angle{PSZ}=90^\circ\bigstar\) 。
在 \(Rt\triangle{PZM}\) 与 \(Rt\triangle{PZS}\) 中,\(PZ=PZ,PS=PM\) 。
所以 \(\triangle{PZM}\cong \triangle{PSM}\) ,因此 \(PZ\) 平分 \(\angle{MPS}\) 。☐
示例: 焦点弦两端的切线成直角,且焦点在准线上。

示例: \(P\) 为抛物线上一点,\(P\) 在准线上的投影是 \(M\) ,在 \(P\) 点的切线上任取一点 \(O\) ,求证:\(OM=OS\) 。
示例: 若抛物线在 \(P_1,P_2\) 的切线相交于点 \(O\) ,且 \(P_1M_1,P_2M_2\) 分别是从 \(P_1,P_2\) 到准线的垂线。 (1) 证明: \(OM_1,OS,OM_2\) 都相等;(2) 由此导出从抛物线外一点 \(O\) 作两条切线的方法。
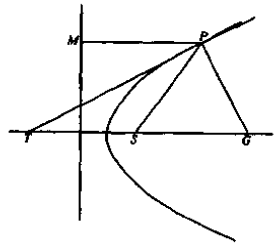
示例: 如果抛物线在其上一点 \(P\) 处的切线、法线分别交轴于 \(T\) 和 \(G\) ,那么 \(SG=SP=ST\) 。
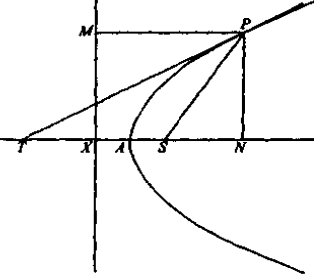
示例: 若在点 \(P\) 处的切线和纵标线分别交轴于 \(T\) 和 \(N\) ,则 \(NT\) 叫做点 \(P\) 的次切线。求证: \(NT=2AN\) 。1
示例: 如果在点 \(P\) 的法线和纵坐标分别交轴于点 \(G\) 和 \(N\) ,那么 \(NG\) 叫做 \(P\) 点处的次法线。求证次法线长度等于焦准距。

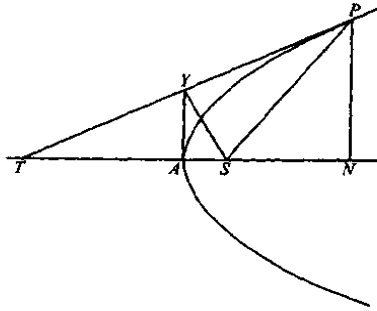
示例: 若抛物线在其任一点 \(P\) 的切线交顶点处的切线于 \(Y\) ,则 \(SY\) 垂直平分 \(PT\) ,且 \(SY\) 是 \(SA\) 与 \(SP\) 的比例中项。
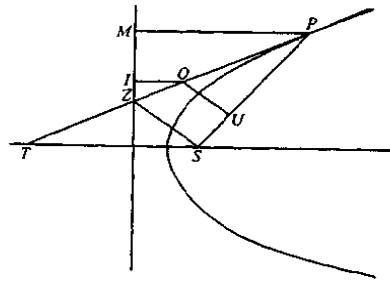
示例: 从抛物线上任一点 \(P\) 处的切线上取一点 \(O\) ,作切线 \(OI\) 垂直于准线, \(OU\) 垂直 \(SP\) ,垂足分别为 \(I\) 和 \(U\) ,那么 \(SU=OI\) 。
示例: 从抛物线外一点 \(O\) 作抛物线的两条切线 \(OQ\) 和 \(OQ'\) 。证明两条切线段到焦点的张角相等,即 \(\angle{OSQ}=\angle{Q'SO}\) ,并且 \(\triangle{SOQ}\sim\triangle{SQ'O}\) 。
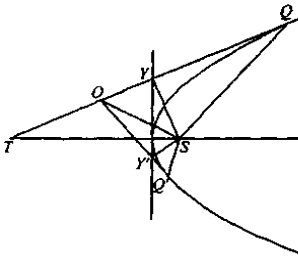
解: 根据命题 10 中的结论,\(SY\) 垂直平分 \(TQ\) ,\(\triangle{STQ}\) 为等腰三角形, \(SY'\perp OQ'\) ,\(QYSY'\) 四点共圆。
所以 \(\angle{SOQ'}=\angle{SYY'}=\angle{T}=\angle{SQO}\)
同理 \(\angle{SOQ}=\angle{SQ'O}\)
因此 \(\angle{OSQ}=\angle{Q'SO}\) ,\(\triangle{SOQ}\sim\triangle{SQ'O}\)☐
示例: 如果作抛物线的一对切线 \(OQ\) ,\(OQ'\) ,并且作平行于轴的直线 \(OV\) ,交 \(QQ'\) 于 \(V\) ,求证 \(QQ'\) 被 \(V\) 平分。
示例: 证明:抛物线的任意一组平行线的中点的轨迹是一条平行于轴的直线,通过平行于这些弦的切线的切点。
定义: 在一条曲线中,一组平行弦的中点轨迹叫做直径。
定义: 夹在直径与曲线之间的半弦称为此直径的纵标线。
示例: 若 \(QV\) 是直径 \(PV\) 的纵标线,且 \(Q\) 点处的切线交 \(VP\) 的延长线于 \(O\) ,则 \(OP=PV\) 。
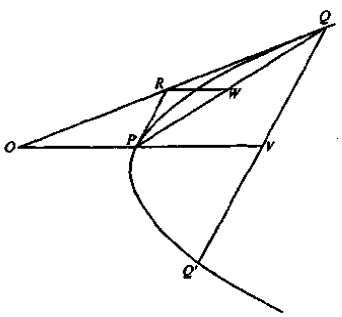
示例: 若 \(QV\) 是直径 \(PV\) 的纵标线,则 \(QV^2=4SP\cdot PV\)
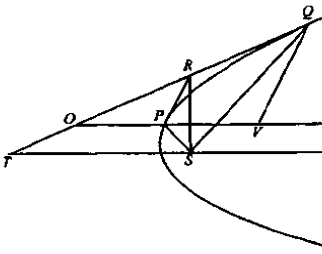
示例: 如果抛物线的焦点弦 \(QSQ'\) 被直径 \(PV\) 平分,其中 \(P\) 是与曲线的交点, \(V\) 是与 \(QQ'\) 的交点。求证: \(QQ'=4SP\) 。
椭圆和双曲线
椭圆的定义
椭圆是到一定点(焦点)的距离与到一直线(准线)距离之比为小于 \(1\) 的常数的点的轨迹。
双曲线是到一定点(焦点)的距离与到一直线(准线)距离之比为大于 \(1\) 的常数的点的轨迹。
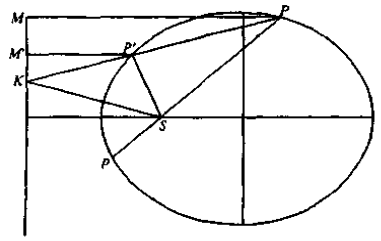
示例: 如果椭圆的弦 \(PP'\) 的延长线交准线于 \(K\) ,那么 \(SK\) 平分 \(SP\) 与 \(SP'\) 所成角的外角。
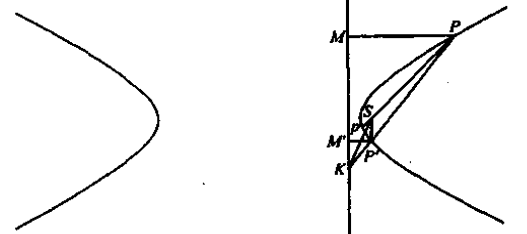
示例: 如果抛物线的弦 \(PP'\) 所在直线(注意有两种情况)交准线于 \(K\) ,那么 \(SK\) 平分 \(SP\) 与 \(SP'\) 所成角的外角。

示例: 设 \(P_1SP_2\) 是椭圆的一条焦点弦, \(X\) 是椭圆的轴与准线的交点