计数原理（二）

集合计数（续）

我们用 \(P(n,r)\) 表示 \(n\) 元素集合的 \(r\) 排列的数目。如果 \(r\geq n\) ，则 \(P(n,r)=0\) 。

集合的排列

定理：对于正整数 \(n\) 和 \(r\) ，\(r\leq n\) ，有 \[P(n,r)=n\times(n-1)\times(n-1)\times\cdots\times2\times1\]

考虑把对象排成一个圆，只要其中一个可以通过旋转与另一个重合就把两个排列看作相同的。即 \(12345,23451,34512,45123,51234\) 都是相同的。

集合的循环排列

定理： \(n\) 元素集合的循环 \(r\) 排列的数目是：\[\dfrac{P(n,r)}{r}=\dfrac{n!}{r\cdot (n-r)!}\]

我们用 \(n \choose r\) 表示 \(n\) 个元素集合的 \(r\) 个元素子集数目。请注意，每个 \(r\) 元素子集都对应一种从 \(n\) 个元素中无序选取 \(r\) 个元素的方法。

集合的 \(r\) 子集（组合）

定理：对于 \(0\leq r\leq n\) ，有 \(P(n,r)=r!{n\choose r}\) 即：\[{n\choose r}=\dfrac{n!}{r!(n-r)!}\]

性质：对于 \(0\leq r\leq n\) 有：\[{n\choose r}={n\choose n-r}\]

帕斯卡公式

定理：（帕斯卡公式）对于所有满足 \(1\leq k\leq n-1\) 的整数 \(n\) 和 \(k\) ，有 \[{n\choose k}={n-1\choose k}+{n-1\choose k-1}\]

多重集合的排列组合

示例：一家面包店有 \(8\) 种炸面包圈。如果一盒内装一打面包圈，那么能够装配多少不同类型的炸面包圈盒？

示例：项取自 \(1,2,\cdots,k\) 的长度为 \(r\) 的非递减序列的个数是多少？（一个序列里的数可以重复）

示例： \(S=\{10\cdot a,10\cdot b,10\cdot c,10\cdot d\}\) 。每一种类型的对象至少出现一次的 \(S\) 的 \(10\) 组合的个数是多少？

示例： \(x_1+x_2+x_3+x_4=20\) 的整数解的个数是多少？其中 \[x_1\geq3,x_2\geq1,x_3\geq0,x_4\geq5\]

二项式定理

设 \(n\) 是正整数。对所有的 \(x,y\) 有：\[(x+y)^n=x^n+{n\choose1}x^{n-1}y+{n\choose2}x^{n-2}y^2+\cdots+{n\choose n-1}xy^{n-1}+y^n\]

用求和记号表示为：\[(x+y)^n=\sum\limits_{k=0}\limits^{n}{n\choose k}x^{n-k}y^k\]

二项式定理（特殊情形）

设 \(n\) 是正整数。对所有的 \(x\) 有：\[(1+x))^n=\sum\limits_{k=0}\limits^{n}{n\choose k}x^{k}=\sum\limits_{k=0}\limits^{n}{n\choose n-k}x^{k}\]

示例：证明： \(k{n\choose k}=n{n-1\choose k-1}\)

示例：证明： \({n\choose0}+{n\choose1}+{n\choose2}+\cdots+{n\choose n}=2^n\)

示例：证明： \({n\choose0}-{n\choose1}+{n\choose2}-\cdots+(-1)^n{n\choose n}=0\)

示例：证明： \(1{n\choose1}+2{n\choose2}+\cdots+n{n\choose n}=n2^{n-1}\)

示例：证明： \({n+1\choose k+1}={0\choose k}+{1\choose k}+{2\choose k}+\cdots+{n-1\choose k}+{n\choose k}\)

示例：求 \((x_1+x_2+\cdots+x_t)^n\) 中 \(x_1^{n_1}x_2^{n_2}\cdots x_t^{n_t}\) 的系数。

示例：用二项式定理证明：\(3^n=\sum\limits_{k=0}\limits^{n}{n\choose k}2^k\)

示例：用二项式定理证明：\(2^n=\sum\limits_{k=0}\limits^{n}(-1)^k{n\choose k}3^{n-k}\)

示例：化简：\({n\choose k}+3{n\choose k-1}+3{n\choose k-2}+{n\choose k-3}\) （写成单个组合数）

鸽巢原理

示例：证明：若 \(a\) 与 \(b\) 互质，则 \(a,2a,3a,\cdots,(b-1)a\) 除以 \(b\) 的余数取遍 \(1,2,\cdots,b-1\) 。

示例：证明：一个有理数 \(\dfrac{a}{b}\) 一定可以写成十进制循环小数。

示例： \(\gcd(m,n)=1\) ，对于任意 \(0\leq a\leq m-1\) 与 \(0\leq b\leq n-1\) ，存在正整数 \(x\) 使得： \(x\) 除以 \(m\) 的余数为 \(a\) ，且 \(x\) 除以 \(n\) 的余数为 \(b\) 。

示例：证明：给定 \(m\) 个整数 \(a_1,a_2,\cdots,a_m\) ，存在满足 \(0\leq k<l\leq m\) 的整数 \(k\) 和 \(l\) ，使得 \(a_{k+1}+a_{k+2}+\cdots+a_l\) 能够被 \(m\) 整除。通俗地说，就是在序列 \(a_1,a_2,\cdots,a_m\) 中存在连续的 \(a\) ，这些 \(a\) 的和能被 \(m\) 整除。

示例：一位国际象棋大师有 \(11\) 周时间备战一项锦标赛，他决定每天至少下一盘棋，但为了不使自己过于疲劳他还决定每周不能下超过 \(12\) 盘棋。证明存在连续若干天，期间这位大师恰好下了 \(21\) 盘棋。

示例：从 \(1~200\) 中选出 \(101\) 个整数，证明其中存在两个整数，其中的一个可以被另一个整除。

示例：有两个圆盘 \(A,B\)，都被分为 \(200\) 个均等的扇形。在圆盘 \(A\) 上任选 \(100\) 个扇形并着红色，其余 \(100\) 着蓝色。在圆盘 \(B\) 中，每一个扇形任意着红或蓝色，红蓝数量没有限制。将两个圆盘中心重合。证明可以通过旋转使得两个圆盘上的同色对齐扇形数目至少是 \(100\) 个。

示例：证明每个由 \(n^2+1\) 个实数构成的序列中，必然存在长度为 \(n+1\) 的递增或递减子序列。

组合与概率

问题： \(4\) 名同学到 \(3\) 个小区参加垃圾分类宣传活动，每名同学只去 \(1\) 个小区，每个小区至少安排 \(1\) 名同学，则不同的安排方法共有 \(\_\_\_\_\_\_\) 种。

问题：将一颗质地均匀的正方体骰子先后抛掷 \(2\) 次，观察向上的点数，则点数和为 \(5\) 的概率是 \(\_\_\_\_\_\_\)

问题：设 \(O\) 为正方形 \(ABCD\) 的中心，在 \(O,A,B,C,D\) 中任取 \(3\) 点，则取到的 \(3\) 点共线的概率为

A. \(\dfrac{1}{5}\)B. \(\dfrac{2}{5}\)C. \(\dfrac{1}{2}\)D. \(\dfrac{4}{5}\)

问题：在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成 \(1200\) 份订单的配货，由于订单量大幅增加，导致订单积压。为解决困难，许多志愿者踊跃报名参加配货工作。已知该超市某日积压 \(500\) 份订单未配货，预计第二天的新订单超过 \(1600\) 份的概率为 \(0.05\) ，志愿者每人每天能完成 \(50\) 份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于 \(0.95\)，则至少需要志愿者

A. \(10\) 名 B. \(18\) 名 C. \(24\) 名 D. \(32\) 名

问题：从 \(6\) 人中选出 \(4\) 人去值班，每人值班一天，若第一天安排 \(1\) 人，第二天安排 \(1\) 人，第三天安排 \(2\) 人，则不同安排方法的种数为 \(\_\_\_\_\_\_\) （结果用数值表示）

问题：已知甲、乙两球落入盒子的概率分别为 \(\dfrac{1}{2}\) 和 \(\dfrac{1}{3}\) ，假定两球是否落入盒子互不影响, 则甲、乙两球都落入盒子的概率为 \(\_\_\_\_\_\_\) ；甲、乙两球至少有一个落入盒子的概率为 \(\_\_\_\_\_\_\)

问题： \(6\) 名同学到甲、乙、丙三个场馆做志愿者，每名同学只去 \(1\) 个场馆, 甲场馆安排 \(1\) 名，乙场馆安排 \(2\) 名，丙场馆安排 \(3\) 名，则不同的安排方法共有

A. \(120\) 种B. \(90\) 种C. \(60\) 种D. \(30\) 种

问题：要安排 3 名学生到 2 个乡村做志愿者, 每名学生只能选择去一个村, 每个村里至少有一名志愿者, 则不同的安排方法共有

A. \(2\) 种B. \(3\) 种C. \(6\) 种D. \(8\) 种

问题：一个盒子里有 \(1\) 个红 \(1\) 个绿 \(2\) 个黄四个相同的球, 每次拿一个, 不放回, 拿出红球即停, 设拿出黄球的个数为 \(\xi\) ，则 \(P(\xi=0)=\_\_\_\_\_\_\) ，\(E(\xi)=\_\_\_\_\_\_\) 。

问题：将 \(5\) 名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶 \(4\) 个项目进行培训, 每名志愿者只分配到 \(1\) 个项目, 每个项目至少分配 \(1\) 名志愿者, 则不同的分配方案共有

A. \(60\) 种B. \(120\) 种C. \(240\) 种D. \(480\) 种

问题：在区间 \((0,1)\) 和 \((1,2)\) 各随机取一个数，则两数之和大于 \(\dfrac{7}{4}\) 的概率为

A. \(\dfrac{7}{9}\)B. \(\dfrac{23}{32}\)C. \(\dfrac{9}{32}\)D. \(\dfrac{2}{9}\)

问题：在区间 \((0,1)\) 随机取一个数，则取到的数小于 \(\dfrac{1}{3}\) 的概率为

A. \(\dfrac{3}{4}\)B. \(\dfrac{2}{3}\)C. \(\dfrac{1}{3}\)D. \(\dfrac{1}{6}\)

问题：袋中有 \(4\) 个红球，\(m\) 个黄球， \(n\) 个绿球。现从中任取两个球，记取出的红球数为 \(\xi\)，若取出两个球都是红球的概率为 \(\dfrac{1}{6}\) ，一红一黄的概率为 \(1/3\) ，则 \(m-n=\_\_\_\_\_\_\) ，\(E(\xi)= \_\_\_\_\_\_\)

问题：已知花博会有四个不同的场馆 \(A,B,C,D\) 。甲、乙两人每人选 \(2\) 个去参观，则他们的选择中恰有一个场馆相同的概率为 \(\_\_\_\_\_\_\)

问题：有六个相同的球，分别标有数字 \(1,2,3,4,5,6\) ，从中有放回的随机取两次，每次取 \(1\) 个球。甲表示事件“第一次取出球的数字是 \(1\)”，乙表示事件“第一次取出球的数字是 \(2\)”，丙表示事件“两次取出球的数字之和是 \(8\)”，丁表示事件“两次取出球的数字之和是 \(7\)”，则 ( )

A. 甲与丙互相独立B. 甲与丁互相独立

C. 乙与丙互相独立D. 丙与丁互相独立

问题：甲口袋中装有 \(2\) 个黑球和 \(1\) 个白球，乙口袋中装有 \(3\) 个白球。现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复 \(n\) 次这样的操作，记甲口袋中黑球个数为 \(X_n\) ，恰有 \(2\) 个黑球的概率为 \(p_n\) ，恰有 \(1\) 个黑球的概率为 \(q_n\) 。

求 \(p_1, q_1\) 和 \(p_2, q_2\) ；
求 \(2p_n+q_n\) 和 \(2p_{n-1}+q_{n-1}\) 的递推关系式和 \(X_n\) 的数学期望 \(E(X_n)\) （用 \(n\) 表示）。

问题：甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束。经抽签，甲、乙首先比赛，丙轮空。设每场比赛双方获胜的概率都为 \(\dfrac{1}{2}\) 。

求甲连胜四场的概率；
求需要进行第五场比赛的概率；
求丙最终获胜的概率。

问题：某校为举办甲、乙两项不同活动，分别设计了相应的活动方案：方案一、方案二。为了解该校学生对活动方案是否支持，对学生进行简单随机抽样，获得数据如下表：

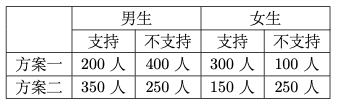
假设所有学生对活动方案是否支持相互独立。

分别估计该校男生支持方案一的概率、该校女生支持方案一的概率；
从该校全体男生中随机抽取 \(2\) 人, 全体女生中随机抽取 \(1\) 人，估计这 \(3\) 人中恰有 \(2\) 人支持方案一的概率；
将该校学生支持方案二的概率估计值记为 \(p_0\) ，假设该校一年级有 \(500\) 名男生和 \(300\) 名女生，除一年级外其他年级学生支持方案二的概率估计值记为 \(p_1\) ，试比较 \(p_0\) 与 \(p_1\) 的大小。（结论不要求证明）

问题：某学校组织“一带一路”知识竞赛, 有 A, B 两类问题。每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束；若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束。 \(A\) 类问题中的每个问题回答正确得 \(20\) 分, 否则得 \(0\) 分；\(B\) 类问题中的每个问题回答正确得 \(80\) 分，否则得 \(0\) 分。已知小明能正确回答 \(A\) 类问题的概率为 \(0.8\) ，能正确回答 \(B\) 类问题的概率为 \(0.6\) ，且能正确回答问题的概率与回答次序无关。

若小明先回答 \(A\) 类问题，记 \(X\) 为小明的累计得分，求 \(X\) 的分布列；
为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由。