圆:基本性质
圆心和弦
做已知圆的圆心 (Euclid III.1)
定理:[命题] 给定一个圆,可以使用尺规作图找到圆心 。
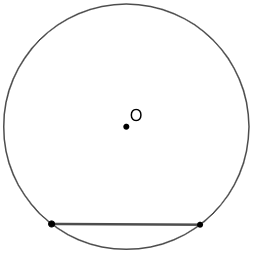
示例: 已知圆 \(O\) ,做出其圆心。

提示,做弦的中垂线即得直径。平分直径即得圆心。
在右侧描述你的做图过程,在下面空白处证明之。在《几何原本》上给出的证明过程使用了反证法。另外,在涉及对称图形的证明中,往往还要用到全等三角形的判定定理。
在证明圆的一些基本性质时,常常用到三角形的一些基本性质和反证法。本示例运用了三角形中大角对大边(Euclid I.19)等性质。
弦的中垂线过圆心 (Euclid III.3)
定理:[命题] 平分弦的直径垂直该弦,反之亦然。
该命题的具体化条件和证明如下:
示例: 已知圆 \(ABC\) ,直线 \(CD\) 过圆心且二等分不过圆心的弦 \(AB\) 于点 \(F\) 。求证: \(CD\) 垂直于 \(AB\)。两圆的位置关系
两圆之间有5种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交。两圆圆心之间的距离叫做圆心距。
相切 (III.6)
定理:[命题] 如果两个圆相切,则圆心不同。
相交 (Euclid III.10)
定理:[命题] 一个圆截另一个圆,交点不多于两个。
内切 (III.11)
定理:[命题] 如果两个圆内切,则圆心连线过切点。
外切 (III.12)
定理:[命题] 如果两个圆外切,则圆心连线过切点。
弦心距
弦长和弦心距(Euclid III.14)
在一个圆中,相等弦的弦心距相等,反之亦然。
示例: 已知圆 \(ABDC\) ,圆内的两条弦 \(AB\) 和 \(CD\) 彼此相等。求证 \(AB\) 和 \(CD\) 的弦心距相等。
示例: (Euclid III.15) 在一个圆中,直径是最长的弦,其它靠近圆心的弦总是比远离的弦长。
圆的切线
切线的存在性和唯一性
平面上过圆的直径的端点做该直径的垂线,则该直线上其它点均落在圆外。且在平面上该直线与圆周之间无法再插入另一条直线。
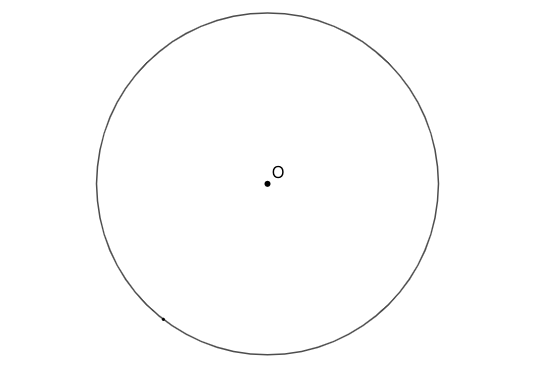
示例: (Euclid III.17) 过圆外给定一点,做已知圆的切线。
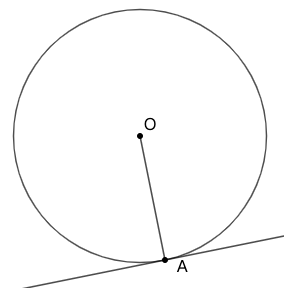
切线和直径(Euclid III.18)
如果一条直线与圆相切,那么连接圆心和切点的直线垂直于切线。
切线和直径(Euclid III.19)
如果一条直线与圆相切,那么过切点作与切线成直角的直线,必经过圆心。
切线长相等
定理:[命题] 圆 \(O\) 的两条切线交于点 \(A\)、 \(B\)、 \(C\) 分别表示两个切点,则 \(AB=AC\) 。
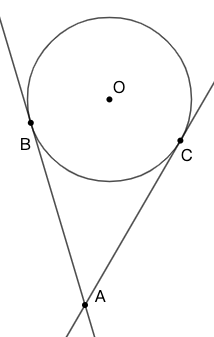
公切线段相等
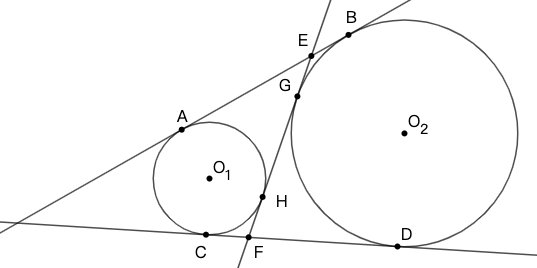
定理:[命题] 圆 \(O_1\) 和 圆 \(O_2\) 相离。设直线 \(AB\)、\(CD\) 是圆 \(O_1\) 和 圆 \(O_2\) 的两条外公切线, \(A,B,C,D,G,H\) 为切点 , \(E,F\) 为外公切线和内公切线的交点。则 \(AB=CD=EF\) 。(若两圆相交,就没有内公切线 \(EF\) ,结论就只有 \(AB=CD\) 。)
注意还要讨论两条外公切线平行的情况
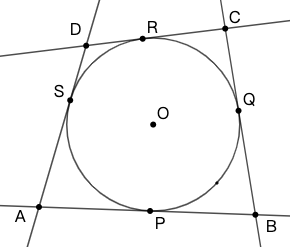
示例: (Pitot Theorem) 求证,若四边形有内切圆,则其对边长度之和相等。
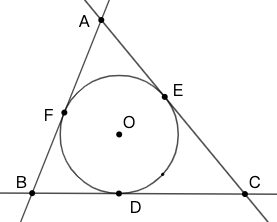
示例: \(\triangle{ABC}\) 内切圆在 \(BC\)、\(CA\) 和 \(AB\) 上的切点,则 \[2\cdot AE=2\cdot AF=-a+b+c\] (对点 \(B\) 、\(C\) 也有类似结论)
弧与圆心角
圆周角定理(Euclid III.20)
在一个圆内,同弧上的圆心角是圆周角的二倍。
示例: 点 \(O\) 为圆 \(\omega\) 的圆心,\(BC\) 为圆 \(\omega\) 的弦,点 \(A\) 在圆上且不与 \(B\) 、\(C\) 重合。则弧 \(BC\) 对应的圆周角 \(\angle{BAC}\) 为其对应的圆心角的一半。
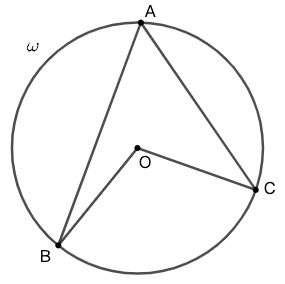
圆周角定理(Euclid III.21,26,27)
在一个圆内(或两等圆),同弧(等弧)所对的圆周角相等。反之亦然。
示例: (Euclid III.22) 求证圆的内接四边形的对角和等于平角。
注意讨论各种情况
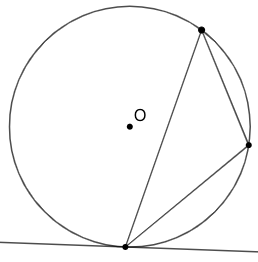
圆切角定理
若直线与圆相切,由切点过圆内作一条直线将圆截成两部分,那么切线与该直线所夹的角等于另一弓形上的角。
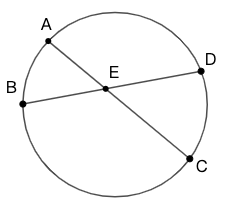
相交弦定理(Euclid III.35)
定理: 如果圆内有两条弦相交,则每条弦的两段构成的矩形面积相等(即如图 10, \(AE\cdot EC=BE\cdot ED\))。
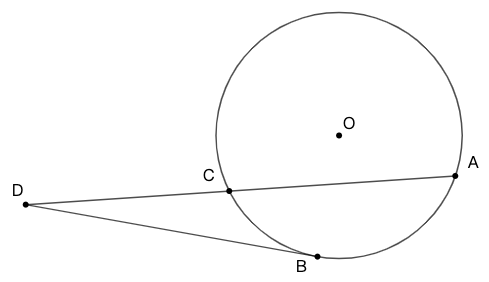
切割弦定理(Euclid III.36,37)
定理: 在圆外任取一点,过该点做两条直线,其一与圆相切,其二与圆相交。那么由圆所截得的整个线段与圆外定点与凸弧之间的一段所构成的矩形,其面积等于切线上的正方形。 反之,若有面积相等,则其一直线为切线。
三角形的五心
外心的存在 (Existence of the Circumcenter)
定理:[命题] 在 \(\triangle{ABC}\) 中, \(AB\) 、 \(BC\) 和 \(CA\) 的中垂线交于一点,称此点为 \(\triangle{ABC}\) 的外心,通常用 \(O\) 表示,它是三角形外接圆的圆心。
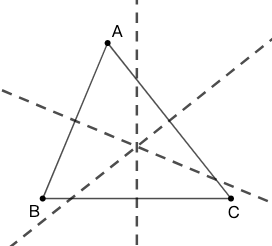
垂心的存在 (Existence of the Orthocenter)
定理:[命题] 在 \(\triangle{ABC}\) 中, 三条高相交于一点,称此点为 \(\triangle{ABC}\) 的垂心,通常用 \(H\) 表示。
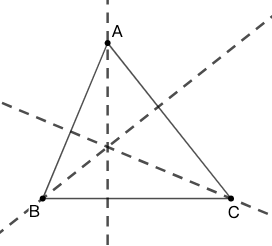
内心的存在 (Existence of the Centroid)
定理:[命题] 在 \(\triangle{ABC}\) 中,一角 \(\angle A\) 的内角平分线与另两角的外角平分线交于一点,称此点为 \(\triangle{ABC}\) 的 \(A-\) 旁心,常用 \(I_a\) 表示,是 \(A-\) 旁切圆(与\(BC\) 以及 \(AB\)、\(AC\)的延长线相切)的圆心。类似地可以定义 \(I_b,I_c\) 。
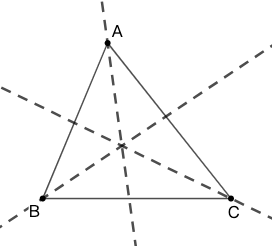
旁心的存在 (Existence of the Excenter)
定理:[命题] 在 \(\triangle{ABC}\) 中,一角 \(\angle A\) 的内角平分线与另两角的外角平分线交于一点,称此点为 \(\triangle{ABC}\) 的 \(A-\) 旁心,常用 \(I_a\) 表示,是 \(A-\) 旁切圆(与\(BC\) 以及 \(AB\)、\(AC\)的延长线相切)的圆心。类似地可以定义 \(I_b,I_c\) 。
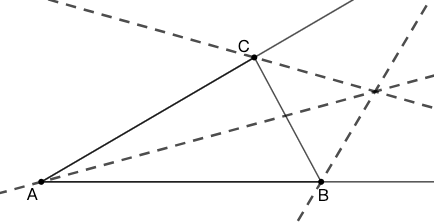
中线交点是三等分点
定理:[命题] 在 \(\triangle{ABC}\) 中,两条中线的交点,是这两条中线的三等分点。
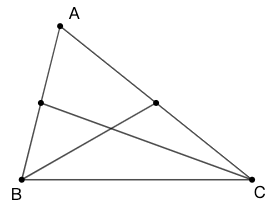
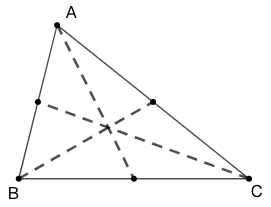
重心的存在 (Existence of the Centroid)
定理:[命题] 在 \(\triangle{ABC}\) 中,三条中线交于一点,称此点为 \(\triangle{ABC}\) 的中心,通常用 \(G\) 表示。
习题
练习:-Page8 命题 11} 在 \(\triangle{ABC}\) 中,点 \(H\)、\(I\)和 \(O\) 分别为其垂心、内心和外心。求证:
若 \(\triangle{ABC}\) 为锐角三角形,则 \(\angle{BHC}=180^\circ-\angle{A}\) 。
\(\angle{BIC}=90^\circ+\dfrac{1}{2}\angle{A}\) 。
若 \(\angle{A}\) 为锐角,则 \(\angle{BOC}=2\angle{A}\) 。
练习: \(ABCD\) 为平行四边形 \(AB>BC\) 。 \(K\)、\(M\) 分别为 \(\triangle{ACD}\) 、\(\triangle{ABC}\) 的内切圆在 \(AC\) 上的切点: \(L\) 、\(N\) 分别为 \(\triangle{BCD}\) 和 \(\triangle{ABD}\) 的内切圆在 \(BD\) 上的切点。求证:四边形 \(KLMN\) 为矩形。
YPMA0208 习题
示例: 如图 18 所示,\(P\) 为两圆公共弦上一点,过 \(P\) 的直线交两圆于 \(C,D,E,F\) 如图所示。
求证:\(\dfrac{CE}{PE}=\dfrac{DF}{PD}\)
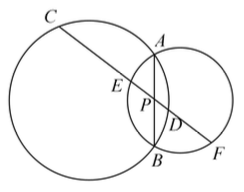
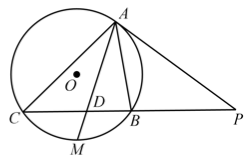
示例: 如图19 所示, \(PA\) 切圆 \(O\) 于点 \(A\),割线 \(PBC\) 交圆 \(O\) 于 \(B\)、\(C\)。 \(M\) 是 \(\wideparen{BC}\) 的中点, \(AM\) 交 \(BC\) 于点 \(D\) 。
求证:\(PD^2=PB\cdot PC\) 。
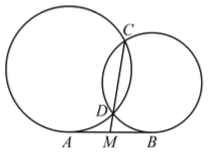
示例: 如图20 所示,两圆交于\(C\)、\(D\),\(AB\) 为公切线,若 \(AB=12,\ CD=9\)
- 求 \(MD\) 的长度 (2) 求证 \(\angle{ADB}+\angle{ACB}=180^\circ\)
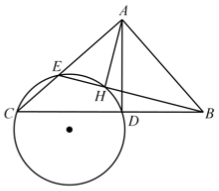
示例: 已知 \(AD\) 为直角 \(\triangle{ABC}\) 斜边上的高,过 \(C\)、\(D\) 两点的圆交 \(AC\) 于 \(E\) ,连 \(BE\) 交该圆于 \(H\) ,连 \(AH\) 。
求证: \(AH\perp BE\) 。
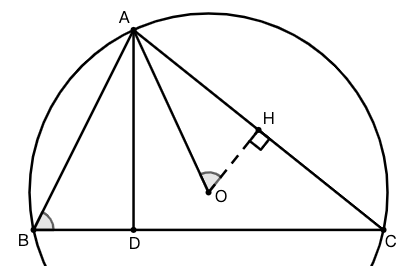
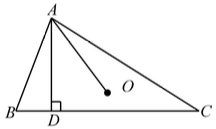
示例: 如图, \(O\) 是 \(\triangle{ABC}\) 的外心, \(AD\perp BC\) 于 \(D\) 。
求证: \(\angle{BAD}=\angle{OAC}\)
证明