角
本章我们来学习“角度”相关的概念。角描述了线之间的关系。
角度的概念
角 (angle)
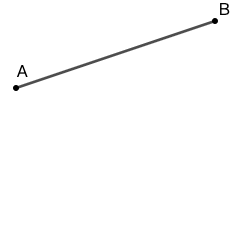
定义: 角 (angle) 由具有共同端点的两条射线 (ray) 组成。这两条射线称为角的边 (side) 。射线的公共端点称为角的顶点 (vertex) 。平面上两条边之间的区域称为角的内部,平面的其余部分称为角的外部。
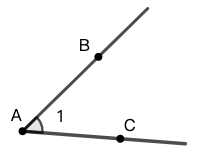
角的命名
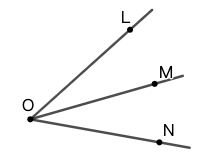
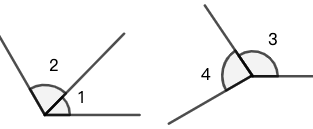
以图 2 为例,你可以使用角的顶点命名它 \(\angle{A}\) ,也可以使用边上的点和顶点命名 \(\angle{BAC}\) 或 \(\angle{CAB}\) (注意你要把表示顶点的字母放在中间)。你也可以使用数字或希腊字母标注,如 \(\angle{1}\) 。
☐
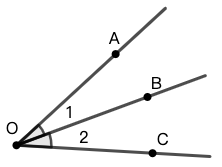
♣ 请注意,在图 3 中,不能使用 \(\angle{O}\) 标记角,因为会产生歧义,无法区分 \(\angle{1}\) 还是 \(\angle{2}\) 。
角的度量(角度制)
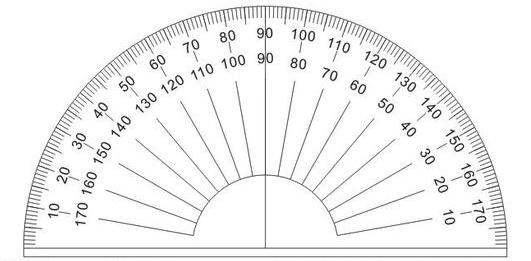
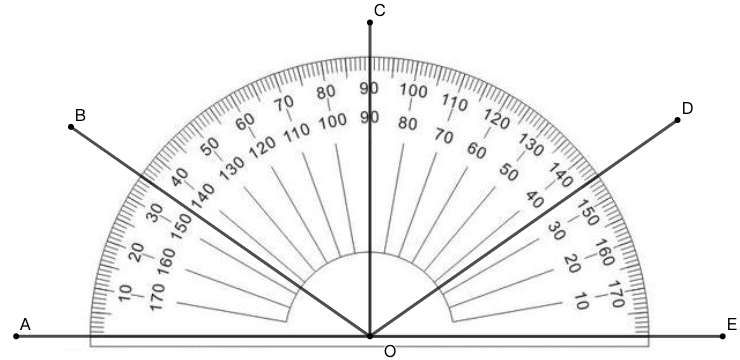
角的度量方法之一是将圆周分为 \(360\) 份,每一份为 \(1^\circ\) ,整个圆周是 \(360^\circ\) 。在绘图时我们常常使用量角器测量角度,如图 4 所示。量角器是半圆形,标刻角度为 \(0-180^\circ\) 。
还有一种度量角度的方法是弧度制,将圆周的角度算为 \(2\pi\) ,然后将不同的角度按比例取值。你在中学会学到弧度制。在小学阶段,无论课内课外,我们都只使用角度制进行计算。
角的种类
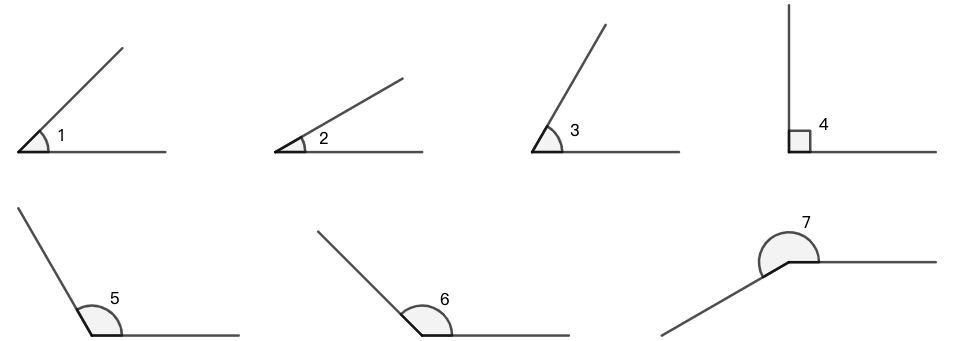
定义: 小于 \(90^\circ\) 的角称为锐角 (acute angle)。等于 \(90^\circ\) 的角称为直角 (right angle) 。大于 \(90^\circ\) 且小于 \(180^\circ\) 的角称为钝角 (obtuse angle) 。等于 \(180^\circ\) 的角称为平角。

示例: 如图 6 所示,计算 \(\angle{BOE}\), \(\angle{COB}\) 和 \(\angle{COE}\) 的值,并指出角的种类(锐角、直角还是钝角)。
示例: 使用量角器,测量图 7 的各个角。
示例: 量一量,在图 8 中,哪些角是相等的?哪些角的和是 \(180^\circ\) ?
示例: 图 9 中有多少个锐角?
定义: 角平分线 (angle bisector)
一个角可以切分成两个相等的角(Euclid I.9)。
定义: 角平分线是从角的顶点引出的一条射线,它将角平分为两个相等的部分。
如图 10 所示, \(OM\) 是 \(\angle{LON}\) 的角平分线。
示例: (Euclid I.9) 使用直尺和圆规,作 \(\angle{AOB}\) 的角平分线。
作图
- [(1)] 在 \(OA\) 上选取一点 \(O_1\) 以 \(O\) 为圆心 \(OO_1\) 为半径做圆,交 \(OB\) 于点 \(O_2\) 。
- [(2)] 选取一个大于 \(O_1O_2/2\) 的半径,分别以 \(O_1\) 和 \(O_2\) 为圆心做圆,则两圆必有交点。
- [(3)] 任取其中一个交点 \(P\) ,则 \(OP\) 即为 \(\angle{AOB}\) 的角平分线。\(\square\)
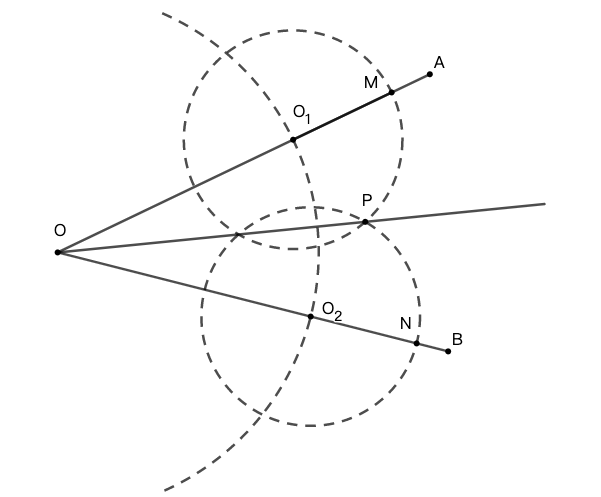
注:说明上述作图过程是角平分线的经典方法是利用全等三角形定理: \(OO_1=OO_2\) ,\(O_1P=O_2P\) , \(OP=OP\) ,因此三角形 \(OO_1P\) 全等于三角形 \(OO_2P\) 。全等三角形定理在《几何原本》中是非常靠前的概念(第八命题 Euclid I.8),但是小学几何学中并不涉及这一定理。
思考与讨论
- 根据上述作图过程,你能说明为什么 \(OP\) 是角平分线么?
- 看看《几何原本》的命题 I.9 ,那里的作图方法和上述示例有什么不同?
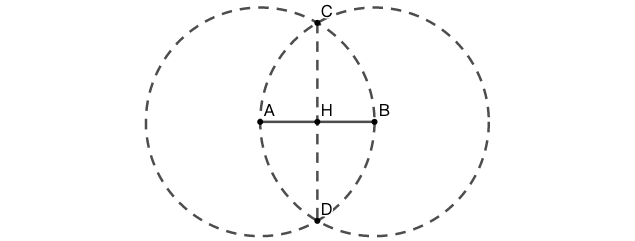
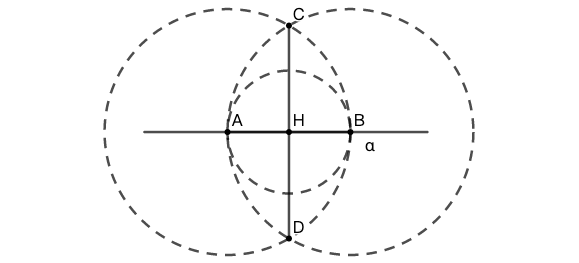
示例: (Euclid I.10) 使用直尺和圆规,将一条线段 (AB) 平分为相等的两部分。
作图 (1) 以 \(AB\) 为半径,分别以 \(A\) 和 \(B\) 为圆心做圆,交于 \(C\) 、 \(D\) 两点。连接 \(CD\) 交 \(AB\) 于 \(H\) ,\(H\) 平分 \(AB\) 。☐
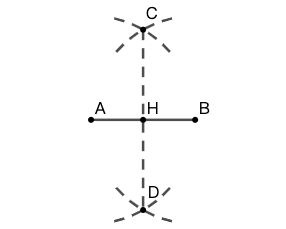
实际作图无需作完整的圆,只要作部分圆弧得到交点即可。以直线等分点的作图为例,无需绘制两个完整的圆,只需目测交点的大概位置,然后绘制小圆弧即可,如图 15 所示。
示例: (Euclid I.11) 过直线上一点,可以做该直线的垂线。
作图
- [(1)] 以 \(H\) 为圆心,任意半径做圆,交直线于 \(A\) 、 \(B\) 两点。
- [(2)] :以 \(AB\) 为半径,分别以 \(A\) 和 \(B\) 为圆心做圆,交于 \(C,D\) 两点。连接 \(CD\) ,必过 \(H\), 即为所求垂线。
☐
将新问题转换为已有问题,是非常重要的数学思想。在本例中,做圆 \(H\) 后,问题即转换为“做线段的中垂线”。
思考与讨论
- 设想你是古人,你手里只有一根长长的绳子,你如何模拟上述作图过程?(平分和垂线)
- 上述问题(过直线上一点做垂线)还可以转化为本讲义已有的其它问题么?
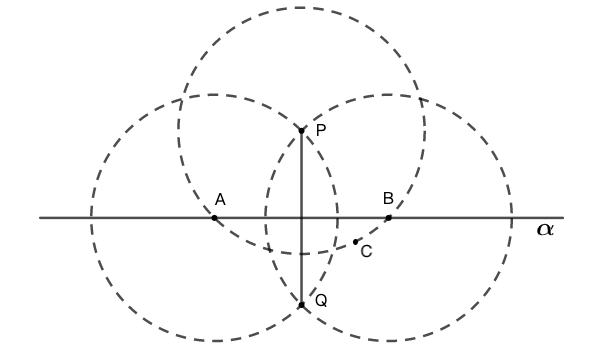
示例: (Euclid I.12) 过直线外一点(点 \(P\) ),可以做该直线的垂线。
作图 (1) 在直线的另一侧取一点 \(C\) ,以 \(PC\) 为半径, \(P\) 为圆心做圆,交直线 \(\alpha\) 于 \(AB\) 两点。 (2) 以 \(PA\) 为半径,\(A\) 和 \(B\) 为圆心分别做圆,两圆相交于 \(P\) 点和另一点 \(Q\) 。 (3) 连接 \(PQ\) ,即为所求做直线 \(\alpha\) 的垂线。\(\square\)
成对的角
邻角 (adjacent angles)
定义: 邻角是指处在同一平面上的两个角,它们有公共顶点,有一条公共边,且无公共的内部点。
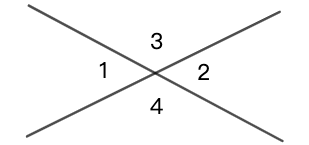
如图 18 所示, \(\angle{1}\) 和 \(\angle{2}\) 是邻角, \(\angle{3}\) 和 \(\angle{4}\) 是邻角。
补角 (supplementary angles) (Euclid I.13/14)
定义: 两个角的和为 \(180^\circ\) ,则称这两个角互为补角。
性质: 两条直线相交,则邻角互为补角。
如图 19 所示,\(\angle{1}\) 和 \(\angle{3}\) 是补角。
请注意,上述从平角得到补角的逆命题也是成立的。即:如果两个邻角的和是 \(180^\circ\) ,那么这两个角的非公共边组成一条直线 (Euclid I.14) 。
对顶角 (vertical angles) (Euclid I.13)
定义: 两个角的边互为对方边的反向延长线(射线),则称这两个角是对顶角。对顶角的范围介于 \(0^\circ\) 与 \(180^\circ\) 之间。
性质: 对顶角相等。
如图 19, \(\angle{1}\) 和 \(\angle{2}\) 是对顶角, \(\angle{3}\) 和 \(\angle{4}\) 是对顶角。
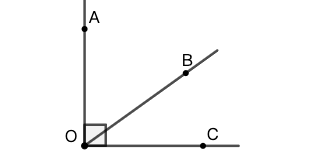
余角 (complementary angles)
定义: 两个角的和为 \(90^\circ\) ,则称这两个角互为余角。
性质: 直角被分成两部分,则两部分互为余角。
如图 20 所示, \(\angle{AOB}\) 和 \(\angle{BOC}\) 互为余角。
♣ 请注意:余角(补角)仅仅是针对角的大小,并不针对角的位置。两个角互为余角(补角),不需要它们是邻角(挨着)。
在几何题目中,补角和余角常常作为隐含的两角之和的数量关系给出,请看如下示例。
示例: 在图 21 中, \(\angle{AOC}\) 是平角。 \(\angle{BOC}\) 的角度是 \(\angle{AOB}\) 的两倍多 \(30\) 度。求 \(\angle{AOB}\) 和 \(\angle{BOC}\) 的度数。
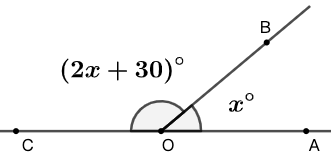
分析这道题本质上就是和倍问题。平角设定和邻角之间的关系给出了角度之间和的关系。
示例: 在图 22 中,哪些角互为余角,哪些角互为补角。
示例: \(\angle{A}\) 和 \(\angle{B}\) 的余角互为余角,那么\(\angle{A}\) 和 \(\angle{B}\) 的补角:
A. 相等 B. 互补 C. 互余 D. 差 \(90^\circ\) E. 和为 \(270^\circ\)
平行线相关的角
平行直线
定义: 平行直线是指在同一个平面内向两端无限延长而不相交的直线。
性质: 过直线外一点,能且只能做一条直线与已知直线平行(Euclid I.31 / 普莱费尔公理)。
♣ “过直线外一点,能且只能做一条直线与已知直线平行”,这是对几何学所探讨的空间进行的前提假设。简单地说,这假设了我们所在的空间是“平直”而非“弯曲”的。虽然我们这里出于直观将其列为“性质”,但它在几何学中的意义远远不是性质。对它的详细讨论超出了小学课内外数学的教学范围。请参见下页材料《平行公设》。
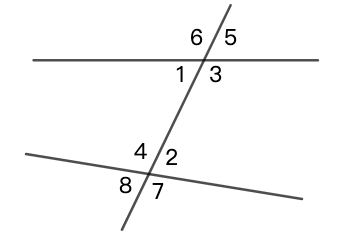
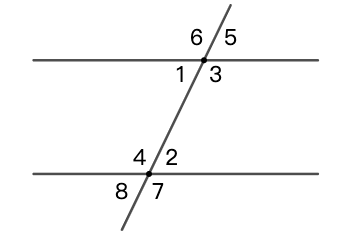
内(外)错角、同位角和同旁内角
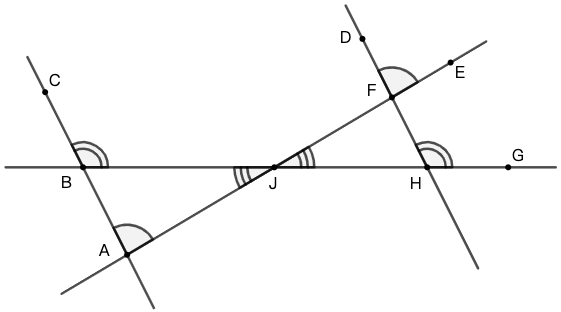
定义: 两条直线被第三条直线所截,会形成内(外)错角、同位角和同旁内角。如图 24 所示:
- \(\angle{1}\) 与 \(\angle{2}\) 是内错角, \(\angle{3}\) 与 \(\angle{4}\) 是内错角;
- \(\angle{6}\) 与 \(\angle{7}\) 是内错角, \(\angle{5}\) 与 \(\angle{8}\) 是内错角;
- \(\angle{4}\) 与 \(\angle{6}\) 是同位角, \(\angle{2}\) 与 \(\angle{5}\) 是同位角;
- \(\angle{1}\) 与 \(\angle{8}\) 是同位角, \(\angle{3}\) 与 \(\angle{7}\) 是同位角。
- \(\angle{1}\) 与 \(\angle{4}\) 是同旁内角, \(\angle{2}\) 与 \(\angle{3}\) 是同旁内角。
性质: 如果一条直线与两条平行线相交,内(外)错角相等,同位角相等,同旁内角互补 (Euclid I.29) 。
性质: 上述性质的逆命题也成立,即:“内错角相等则两直线平行”(对于其它角,也有类似结论)(Euclid I.27/28)。
示例: 根据平行线所成角的性质判断,在图 25 中,哪些角相等?哪些角互补?

(选读)平行公设 - 维基百科
平行公设(英语:Parallel postulate),也称为欧几里得第五公设,因是《几何原本》五条公设的第五条而得名。这是欧几里得几何一条与别不同的公理,比前四条复杂。公设是说:
如果一条线段与两条直线相交,在某一侧的内角和小于两直角和,那么这两条直线在不断延伸后,会在内角和小于两直角和的一侧相交。
假定所有欧几里得公设(当中包括平行公设)都成立的几何称为欧几里得几何。假定平行公设不成立的称为非欧几里得几何。……
欧几里得几何的有些性质与平行公设等价,也就是假设平行公设成立,可推导出这些性质,反过来假设这些性质的一项为公理,也可以推导出平行公设。其中最重要的一项,也是最常作为公理代替平行公设的,要算是苏格兰数学家约翰·普莱费尔提出的普莱费尔公理:
给定一条直线,通过此直线外的任何一点,有且只有一条直线与之平行。
这里有个问题要提出来,即在证明第五公设时,平面是不加定义,如果平面作如下定义:满足第五公设的面定义为平面。这实际上可用公理法对平面作定义。如果有这定义,第五公设是自明的。这才符合直观。
很多人尝试用前四条公设证明平行公设都不成功,反而创造了违反平行公设的双曲几何。最后由意大利数学家贝尔特拉米(Eugenio Beltrami)证明了平行公设独立于前四条公设。
很多与平行公设等价的命题,似乎与平行线无关。有些性质更看似很明显,因而被一些声称证明了平行公设的人不经意用到了。这里是一些命题:
- 三角形内角和为两直角。
- 所有三角形的内角和都相等。
- 存在一对相似但不全等的三角形。
- 所有三角形都有外接圆。
- 若四边形三个内角是直角,那么第四个内角也是直角。
- 存在一对等距的直线。
- 若两条直线都平行于第三条,那么这两条直线也平行。
在初等教育阶段我们不关心平行线的千年恩怨。引入平行线形成的这些角(内错角,同位角和同旁内角)的主要目的是在下一章中推导三角形的内外角的数量关系。
三角形的分类
等边和等腰三角形
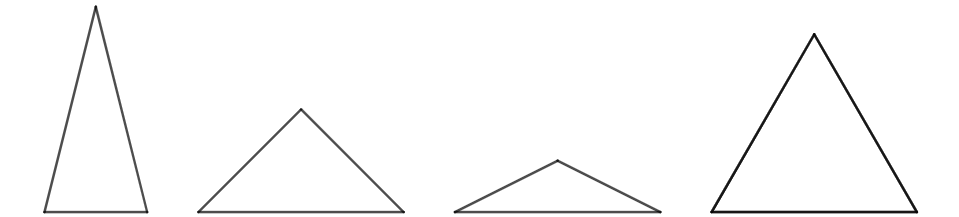
定义: (Euclid Def-I.20) 三角形中,三条边相等的称等边三角形,两条边相等的称等腰三角形,各边都不相等的称不等边三角形 。
等腰三角形中两条相等的边称为“腰”,其对角称“底角”。
图 27 所示均为等腰三角形,其中最右侧的是等边三角形。
等腰/等边三角形的性质
性质: 等腰三角形两底角相等 (Euclid I.5)
请注意:上述命题的逆命题也是成立的:
性质: 有两个角相等的三角形是等腰三角形(Euclid I.6)
性质: 等边三角形的三个内角相等,反之亦然,三个内角相等的三角形是等边三角形。
示例: (Euclid I.1) 使用直尺和圆规,以给定线段 \(AB\) 为边,做等边三角形。
作图
- [(1)] 以 \(AB\) 为半径,\(A\) 和 \(B\) 为圆心分别做圆。
- [(2)] 两圆交于两点,任取一个交点 \(C\) 连接 \(AC\) 和 \(BC\) , \(ABC\) 即为所求做的等边三角形。
☐
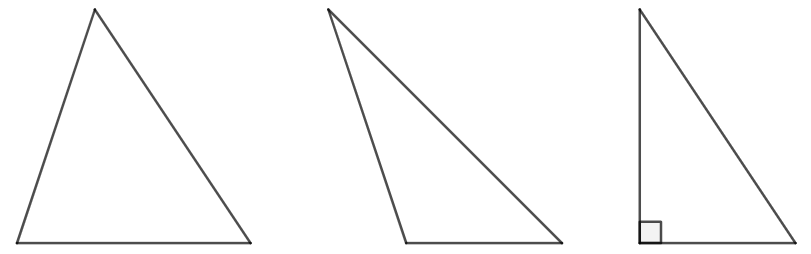
锐角、钝角和直角三角形
定义: 锐角三角形是所有内角均为锐角的三角形。
定义: 钝角三角形是其中一角为钝角的三角形。
定义: 直角三角形是有一个角是直角的三角形。
三角形的稳定性
性质: 三角形稳定性:当一个三角形的三边长度均确定时,三角形的面积和形状都不会改变。
定理: 如果两个三角形有三边对应相等,那么这两个三角形的所有对应角都相等 (全等三角形定理,Euclid I.8 )。
三角形的稳定性在构造建筑物或其它结构时有着重要作用,例如图 31 所示的铁路桥。

思考与讨论
- 你如何证明上述全等三角形定理?
- 你需要几个条件(关于边和角),才能唯一确定一个三角形呢?(这实际上是三角形的三种全等判定方法 Euclid I.4/8/26)
三角形的角
三角形的内角和定理
定理: 三角形的内角和是 \(180^\circ\) 。延长三角形任意一边所形成的外角,等于另外两个内角的和。(Euclid I.32)
定理是那些不那么明显的性质。定理往往需要论证才能让人信服。我们将以三角形内角和为 \(180^\circ\) 这一定理的证明向你展示几何证明的过程。
一般来说,你会在课堂上学到用内错角相等性质证明三角形内角和定理,下面的示例就是这样进行证明。但其实这些命题都是等价的,它们都等价于平行公设。
示例: 用平行线及相关角的性质,证明三角形内角和定理。
证明 在任意 \(\triangle{ABC}\) 中,任取一顶点(如 \(A\))做对边(如 \(BC\))的平行线,如图 32 所示。(普莱费尔公理保证了这条平行线一定能做出来)
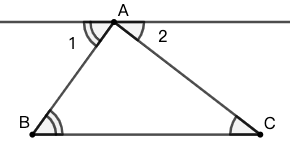
\(\angle{1}=\angle{B}\) 且 \(\angle{2}=\angle{C}\) (平行线的内错角相等)
\(\angle{A}+\angle{1}+\angle{2}=180^\circ\) (平角等于 \(180^\circ\))
因此,\(\angle{A}+\angle{B}+\angle{C}=180^\circ\)
综上所述,命题得证。\(\square\)
这是很多教科书上的证明方法。在下面的思考题中,我们给出欧几里得本人使用的图。
思考与讨论
- 利用图 33 证明上述三角形的内角和为 \(180^\circ\) 及外角等于两内角之和的性质。
- 《几何原本》的第五公设是“同一平面内的两条直线与第三条直线相交,若其中一侧的两个内角之和小于二直角,则该两直线必在这一侧相交”。这是欧几里得几何学对空间性质的基本假设。尝试理解这个公设和“三角形内角和是 \(180^\circ\)”这一命题的等价性。
- 阅读《几何原本》至“三角形内角和定理”(命题 I.32),感受欧几里得创建的公理体系。
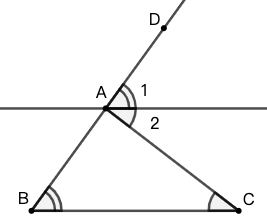
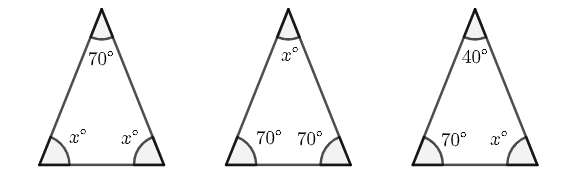
示例: 等腰三角形的两个角分别为 \(70^\circ\) 和 \(x^\circ\) 。 \(x\) 所有可能的值的和是多少?
解: 所有可能的情况如图 34 所示, \(x\) 的值可能是 \(55\), \(40\) 和 \(70\) 。
答案是 \(55+40+70=165\) 。 \(\square\)
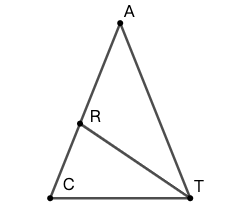
示例:1 在 \(\triangle{CAT}\) 中, \(\angle{ACT}=\angle{ATC}\) 且 \(\angle{CAT}=40^\circ\) 。如果 \(TR\) 平分 \(\angle{ATC}\) ,那么 \(\angle{CRT}\) 是多少度?
示例: 图 36 中, \(\angle{A}=22^\circ\) , \(\angle{AFG}=\angle{AGF}\) 。求 \(\angle{B}+\angle{D}\) 的值。
解: 利用上述三角形的内角外角数量关系 (Euclid I.32) 计算:
\(\angle{AFG}+\angle{AGF}+\angle{A}=180^\circ\) (三角形内角和)
\(2\angle{AFG}+22^\circ=180^\circ\) (\(\angle{A}=22^\circ\), \(\angle{AFG}=\angle{AGF}\))
\(\angle{AFG}=(180^\circ-22^\circ)/2=79^\circ\) (等量运算规则)
\(\angle{B}+\angle{D}=\angle{AFG}\) (外角等于两内角和)
综上所述,\(\angle{B}+\angle{D}=79^\circ\) \(\square\)
思考与讨论
- 上述问题的题设条件能将图形完全确定么?
- 请绘制几个不同但符合题意的图形。
示例: 如图 37 ,求 \(\angle{A}\) 的角度。
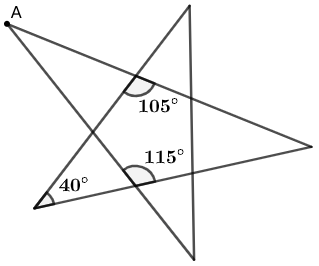
解: 本题依然是使用三角形的角度关系求解。当图中的标注不够时,你要自行补充一些标注,如图 38 所示。
\(\angle{B}=180^\circ-105^\circ=75^\circ\) (平角是 \(180^\circ\) )
\(\angle{C}=115^\circ-40^\circ=75^\circ\) (对顶角相等,外角等于两内角和)
\(\angle{A}=180^\circ-\angle{B}-\angle{C}=30^\circ\) (三角形内角和为 \(180^\circ\) )
综上所述, \(\angle{A}=30^\circ\) \(\square\)
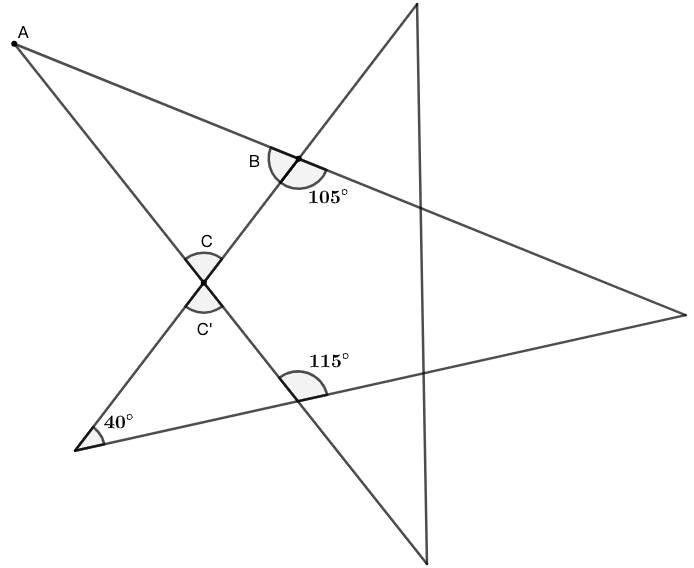
思考与讨论
- 如何绘制题目描述的图形?
- 如果把 \(40^\circ\) 的角改小 \(10^\circ\) 变为 \(30^\circ\),\(\angle{A}\) 的角度如何变化?
- 随着 \(40^\circ\) 的角不断变小,图形从直观上如何变化?
多边形的角
多边形
定义: 多边形是平面的封闭图形,由三条或以上的线段首尾连接组成。
定义: 简单多边形是边不相交的多边形。简单多边形能将平面分成两个区域,即区内和区外。
定义: 凸多边形的内角都不大于 \(180^\circ\) 的简单多边形。不是凸多边形的简单多边形是凹多边形。
如图 39 所示,左起第一个和第二个图形是凸多边形,第三个和第四个是凹多边形,这四个多边形都是简单多边形。

凸多边形的外角和定理
定理: 简单多边形的内角和是 \((n-2)\cdot180^\circ\) ,其中 \(n\) 是多边形的边数。
定理: 凸多边形的外角和是 \(360^\circ\) 。
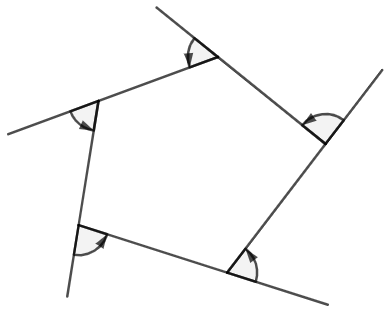
你可以用图 40 理解凸多边形的外角和。你想象自己从一个顶点出发,沿着多边形走一圈,每次经过一个顶点,拐过一个外角的角度。一圈走下来,你也正好转过一圈 \(360^\circ\) 。
这就是外角和是 \(360^\circ\) 的直观道理。自然内角和就是顶点(边)的数目乘以 \(180^\circ\) 再减去外角和(\(360^\circ\))
思考与讨论
- 上述“证明过程”的逻辑链条有什么破绽?
- 你能构建一个严格的证明么?
- 凸多边形的外角和定理能推广至凹多边形么?
- 上述定理能推广至非简单多边形么?
- 你能写出正多边形的内角及外角的计算公式么?
四边形的内角和性质
性质: 简单四边形的内角和是 \(360^\circ\)。
性质: 简单四边形的三个内角之和等于另一内角在圆周角上的邻角。
上述性质是多边形内角和的直接推论。这些性质对凸四边形和凹四边形都成立。如图 41 所示, \(\angle{A}+\angle{B}+\angle{C}=\angle{1}\) 。
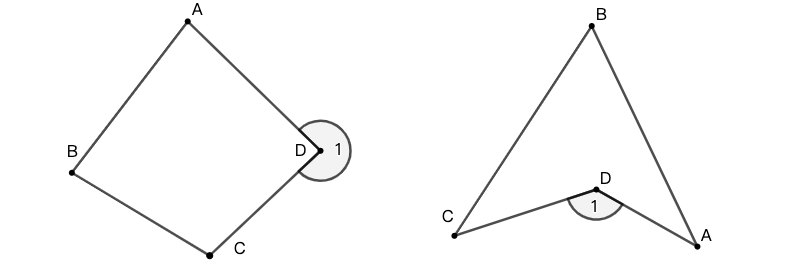
示例: 如图 42 所示,求 \(\angle{A}+\angle{B}\) 的值。
解: 从图形中抽取核心的四边形 \(ABCD\) 。
\(\angle{1}=110^\circ\) (对顶角相等)
\(\angle{A}+\angle{B}+\angle{D}=\angle{1}=110^\circ\) (四边形内角和性质)
\(\angle{A}+\angle{B}=110^\circ-\angle{D}=70^\circ\) (\(\angle{D}=40^\circ\))
综上所述,\(\angle{A}+\angle{B}=70^\circ\) 。 \(\square\)
思考与讨论
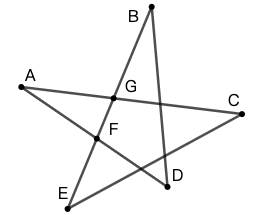
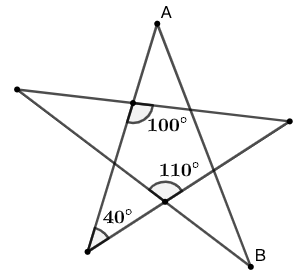
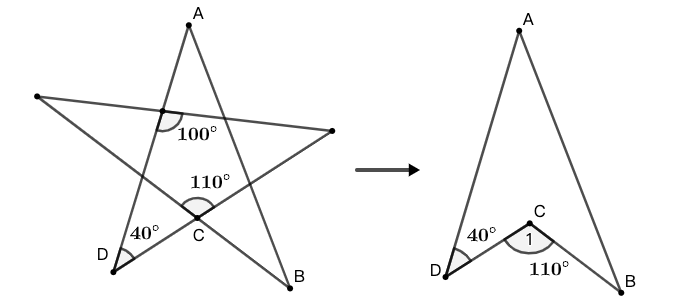
- 求五角星的五个角的度数之和。即如图 44 所示的 \(\angle{A}+\angle{B}+\angle{C}+\angle{D}+\angle{E}\) 。
- 你能将结论推广至“多角星”么?
做图训练
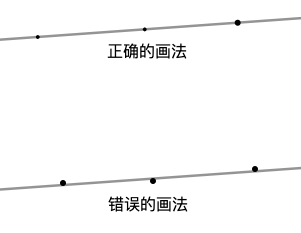
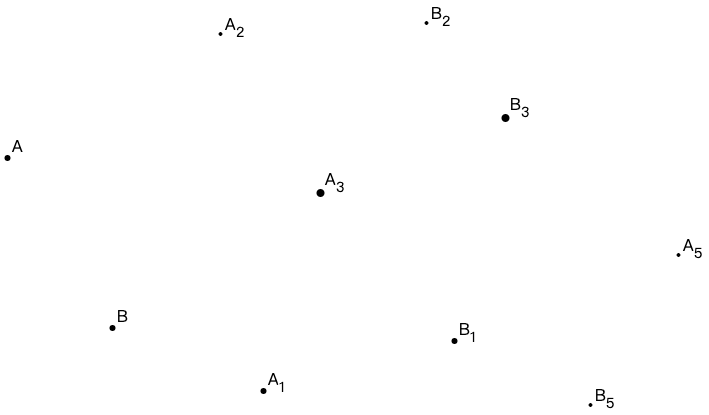
练习: 做直线 \(A_1B_1\)、\(A_2B_2\)、\(A_3B_3\)、\(A_4B_4\)、\(A_5B_5\) 两点做直线。注意:你绘制的直线要均匀穿过点的中心
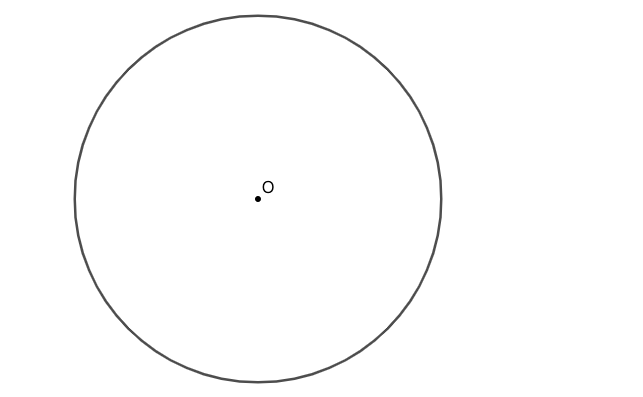
练习: 以给定圆心 \(O_k\) ,过给定点 \(C_k\) 做圆。 注意:你绘制的圆要均匀穿过点的中心

练习: 以给定线段 \(AB\) 为一条边,做等边三角形。
练习: 绘制圆内接正六边形
练习: 以线段 \(AB\) 为底,\(CD\) 长度为腰的长度,做等腰三角形。
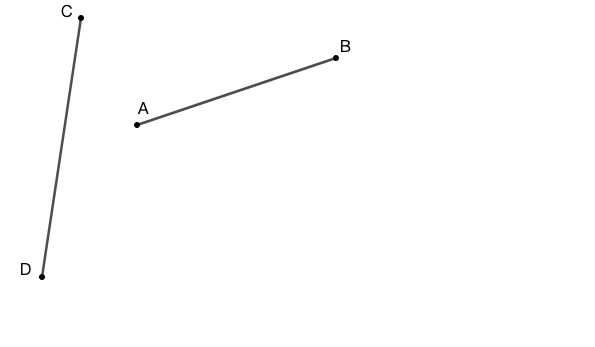
练习: 以线段 \(AB\) 为一腰,\(CD\) 长为底边长,做等腰三角形。

练习: 使用直尺和圆规,做线段 \(AB\) 的垂直平分线。

练习: 使用直尺和圆规,过直线上一点 \(A\) 做直线的垂线。
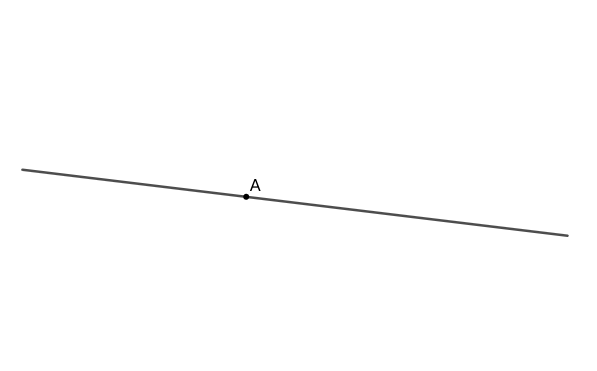
练习: 使用直尺和圆规,过直线外一点 \(A\) 做直线的垂线。
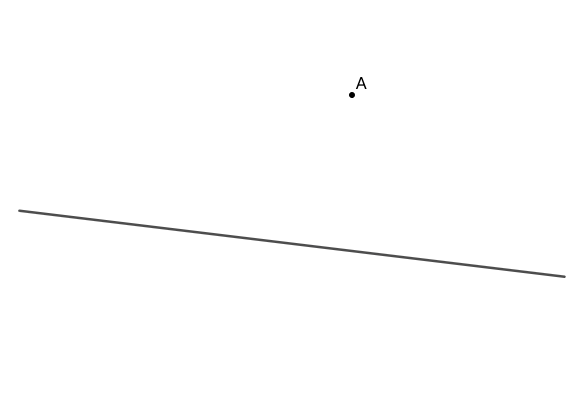
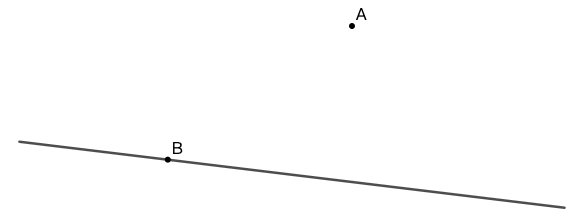
练习: 使用直角尺或带直角刻度线的尺子,过直线外一点 \(A\) 及直线上一点 \(B\) 分别做直线的垂线。
练习: 做出\(\triangle{ABC}\) 关于给定直线的对称图形。
练习: 做出\(\triangle{ABC}\) 关于点 \(O\) 的中心对称图形。
基础练习
练习: 在图 46 中,有多少个锐角,又有多少个钝角?
练习: \(\angle{A}\) 和 \(\angle{B}\) 互为余角。 \(\angle{A}\) 比 \(\angle{B}\) 大 \(10^\circ\) 。\(\angle{A}\) 和 \(\angle{B}\) 的度数各是多少?
练习: \(\angle{A}\) 的补角是 \(\angle{A}\) 的余角的四倍。 \(\angle{A}\) 的度数是多少?
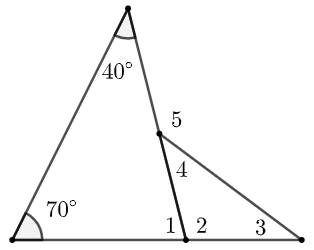
练习:2 在图 47 中, \(\angle{1}+\angle{2}=180^\circ\) , \(\angle{3}=\angle{4}\) 。求 \(\angle{5}\) 的度数。
练习: 计算正五边形和正六边形的外角及内角度数。
练习: 使用量角器及其它绘图工具,绘制正五边形。
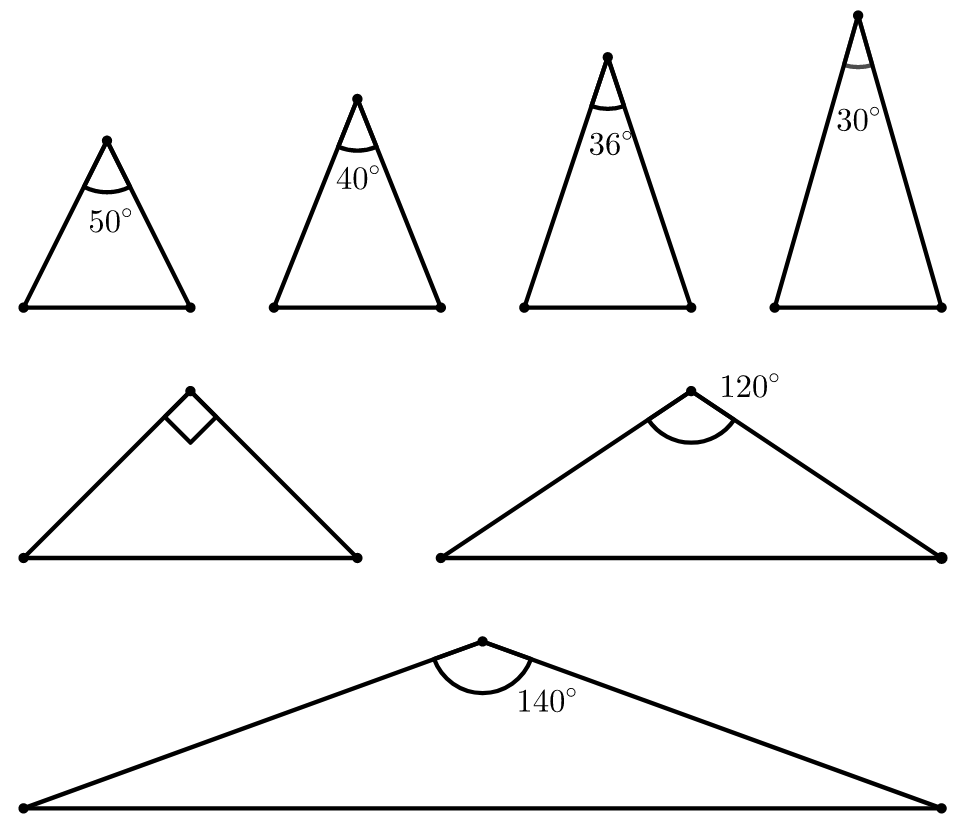
练习: 根据图 49 各个等腰三角形的顶角度数求对应的底角度数。
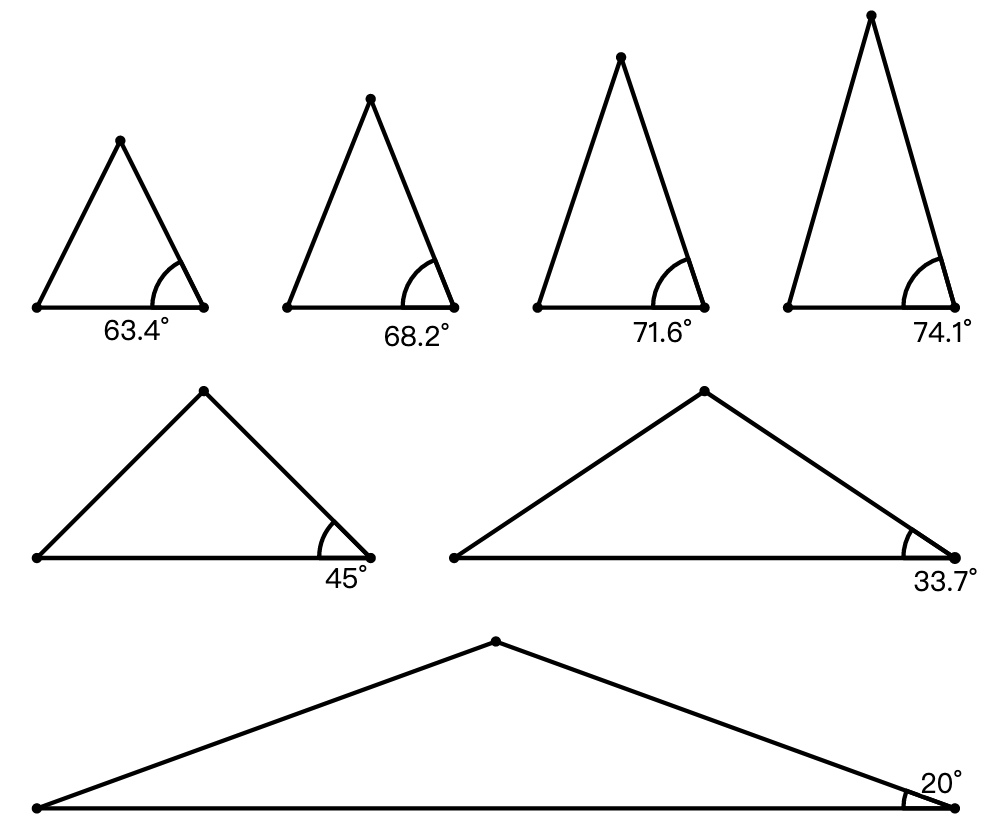
练习: 根据图 50 各个等腰三角形的底角度数求对应的顶角度数。
练习: 套公式求图 51 各个等腰三角形的未知底角或顶角的度数。 \[\begin{align*} base&=\dfrac{180^\circ-top}{2}\\ top&=180^\circ-base\cdot2 \end{align*}\]
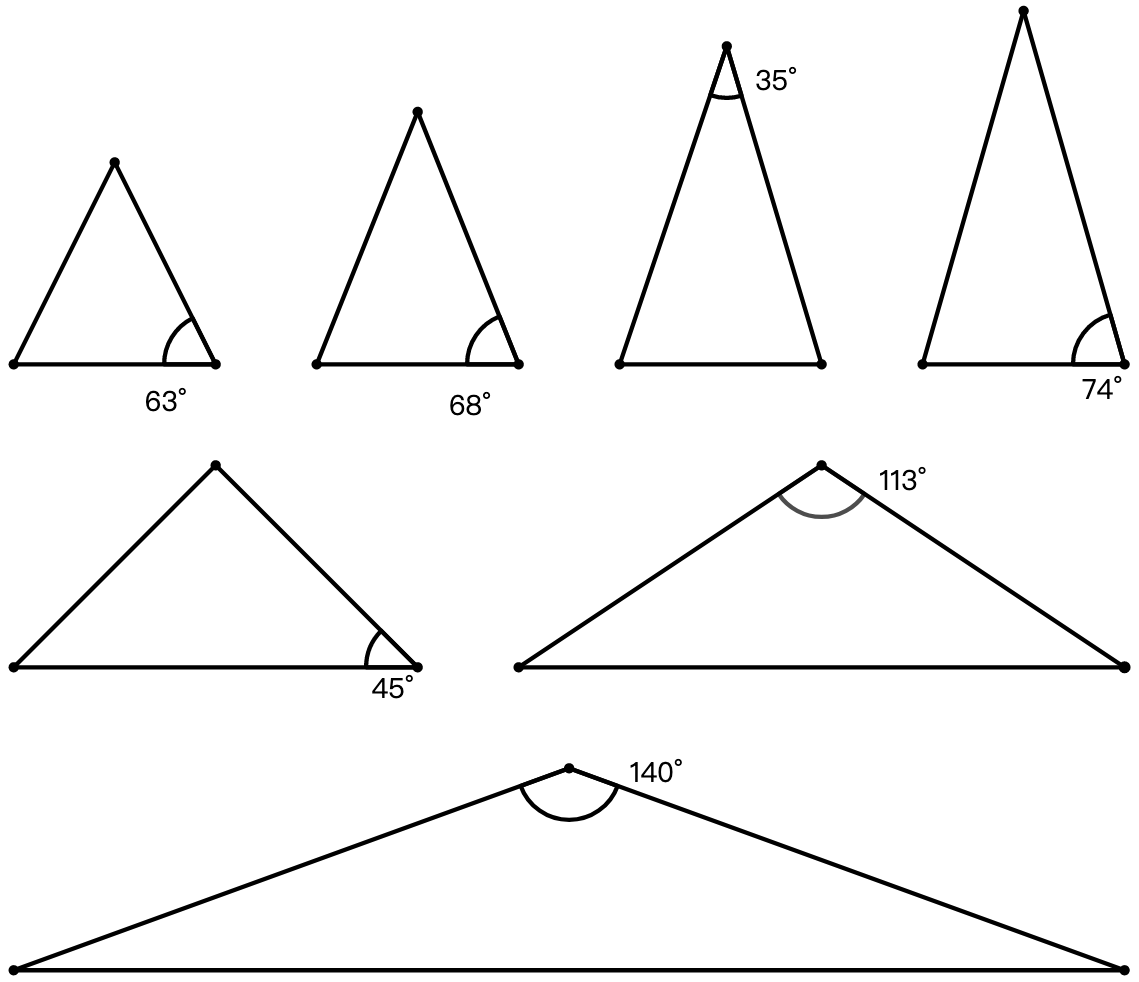
示例:针对第一个图:\(base=63^\circ\) \[top=180^\circ-base\cdot2=180^\circ-63^\circ\cdot2\]
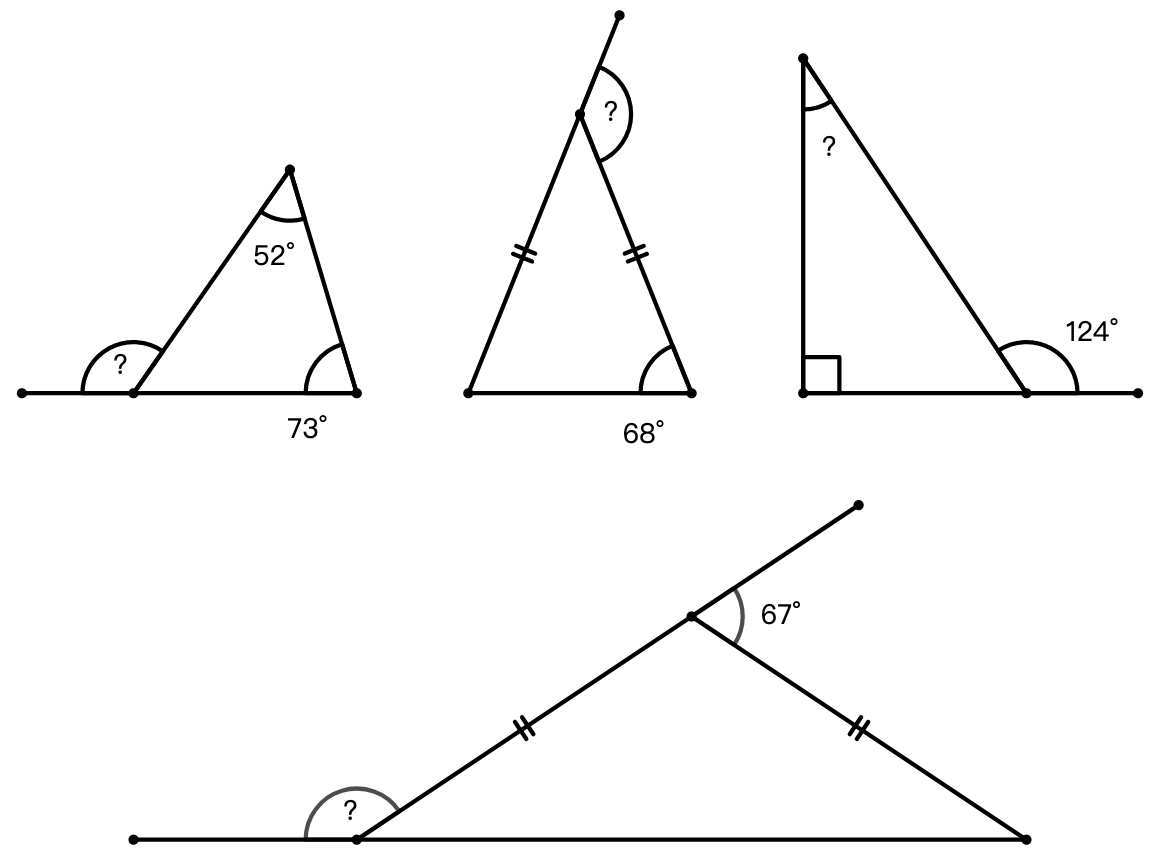
练习: 求图 52 中问号标示的角的度数。
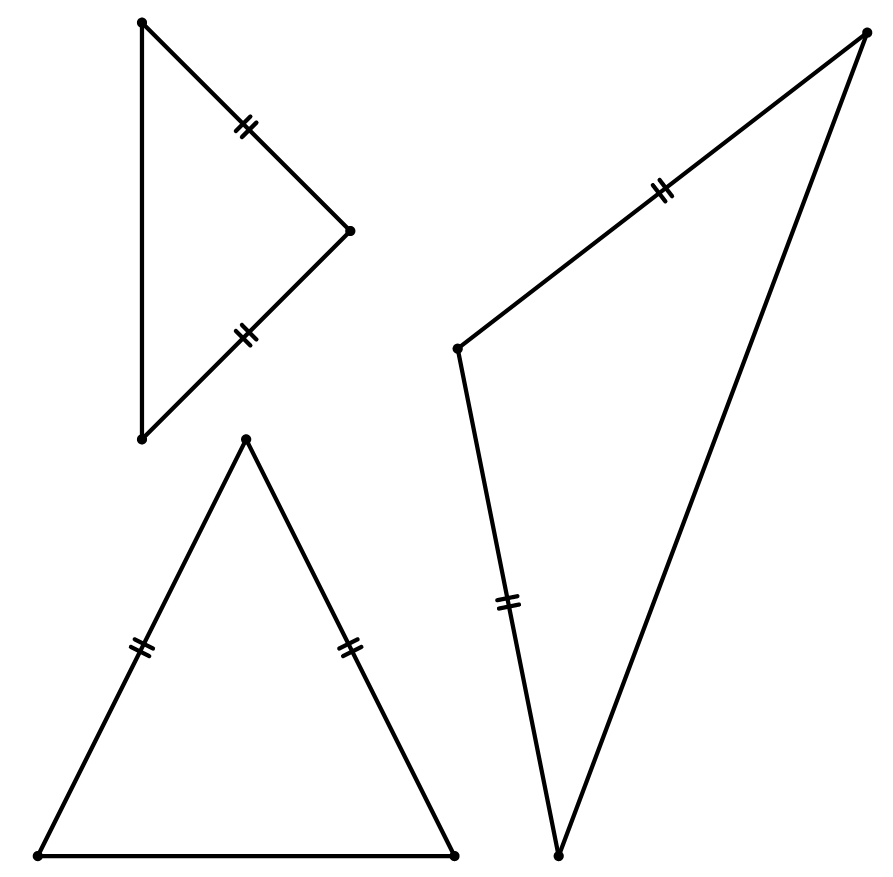
练习: 做出图 53 所示各等腰三角形的对称轴
综合习题
和差倍问题
某个角是自身补角的两倍,这个角的度数是多少?
3 某个角的余角是补角的 \(\dfrac{1}{3}\) ,这个角的度数是多少?
4 某个角的补角是余角的两倍半,这个角的度数是多少?
5 一个角,余角是补角的 \(\dfrac{1}{7}\) 。该角的余角是多少度?
A. \(15^\circ\) B. \(60^\circ\) C. \(75^\circ\) D. \(105^\circ\) E. \(120^\circ\)
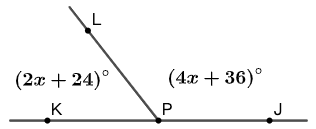
6 如图 54 所示, \(\angle{KPL}\) 和 \(\angle{JPL}\) 互为补角。 \(\angle{KPL}=(2x+24)^\circ\) , \(\angle{JPL}=(4x+36)^\circ\) 。求 \(\angle{KPL}\) 和 \(\angle{JPL}\) 的度数。
7 一个锐角,它的补角的两倍比余角的五倍多 \(27^\circ\) 。求该锐角的角度。
A. \(17^\circ\) B. \(23^\circ\) C. \(31^\circ\) D. \(39^\circ\) E. \(47^\circ\)
在 \(\triangle{ABC}\) 中, \(\angle{B}\) 是 \(\angle{A}\) 的两倍, \(\angle{C}\) 是 \(\angle{B}\) 的两倍还多 \(5^\circ\) 。求 \(\triangle{ABC}\) 三个内角的度数。
等腰三角形及直角三角形
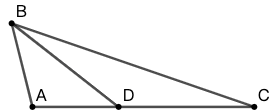
8 如图 55 所示, \(AB=AD\) , \(BD=CD\) , \(\angle{C}=19^\circ\) 。求 \(\angle{A}\) 的度数。
9 图 56 中,\(AC=CD\) , \(\angle{CAB}-\angle{ABC}=40^\circ\) 。求 \(\angle{BAD}\) 的度数。
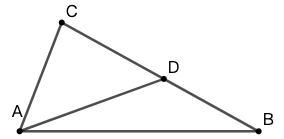
10 如图 57 所示, \(\angle{ABC}=55^\circ\) , \(\angle{ACB}=45^\circ\) , \(CA=DA\) 。求 \(\angle{DCB}\) 的度数。
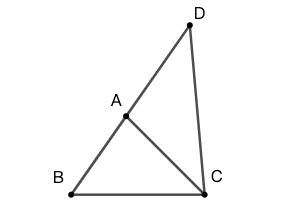
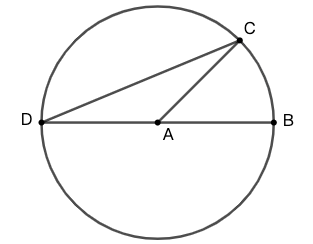
11 如图 58 所示, \(B C D\) 三点在以 \(A\) 为圆心的圆上, \(\angle{CAB}=45^\circ\) 。求 \(\angle{CDB}\) 的度数。
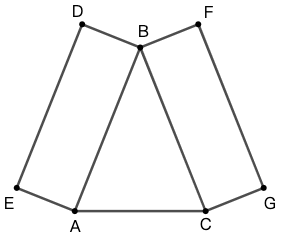
12 图 63 中 , \(AB=CB\) , \(ABDE\) 和 \(CBFG\) 是矩形, \(\angle{BAC}=70^\circ\) 。 求 \(\angle{DBF}\) 的度数。
13 图 60 中, \(\angle{DAB}=30^\circ\) , \(AB=AC\) ,\(BD=CD\) ,\(AE=AD\) ,求 \(\angle{EDC}\) 的度数。
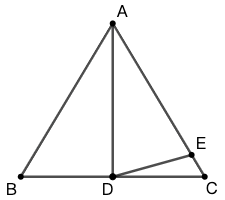
图 61 所示,在 \(\triangle{ABC}\) 中, \(D\) 是 \(AC\) 上一点, \(AB=AD\) ,\(\angle{CBD}=18^\circ\) 。求 \(\angle{ABC}-\angle{ACB}\) 的度数。
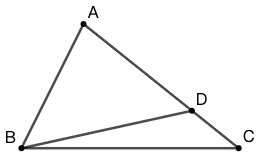
14 如图 62 所示, \(\angle{A}=90^\circ\) ,则 \(\angle{C}+\angle{D}=\)
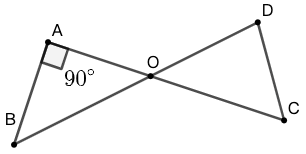
A. \(2\angle{B}\) B. \(90^\circ+\angle{B}\) C. \(180^\circ-\angle{B}\)
D. \(180^\circ-2\angle{B}\) E. \(90^\circ-\angle{b}\)
15 图 63 中 , \(\angle{ABC}=110^\circ\) , \(\angle{C}\) 是直角。求 \(\angle{CDF}\) 的度数。
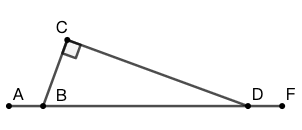
16 图 64 中, \(DF\) 与 \(CB\) 相交于点 \(E\) , \(DA\) 和 \(CB\) 相交于点 \(C\) , \(AB\) 和 \(DF\) 相交于点 \(F\) , \(DF\perp BA\) , \(\angle{FEC}=160^\circ\) , \(\angle{A}=\angle{B}\) 。求 \(\angle{ECA}\) 的度数。
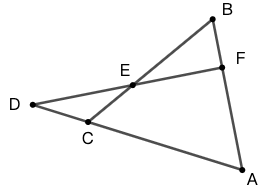
角平分线相关问题
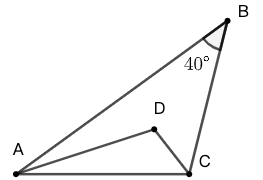
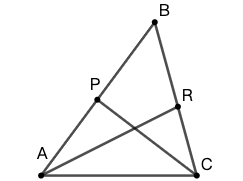
17 图 65 中,\(\angle{B}=40^\circ\) , \(\triangle{ABC}\) 的两条内角平分线交于点 \(D\) 。求 \(\angle{ADC}\) 的度数。
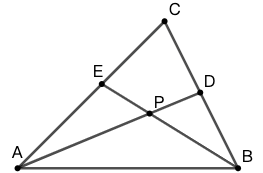
18 图 66 中,\(\angle{C}=70^\circ\) , \(\triangle{ABC}\) 的两条内角平分线 \(BE\) 和 \(AD\) 交于点 \(P\) 。求 \(\angle{APE}\) 的度数。
19 在图 67 中, \(\triangle{ABC}\) 的外角平分线 \(TB\) 和 \(CQ\) 交于点 \(Q\) ,则 \(\angle{BQC}\) 的角度:
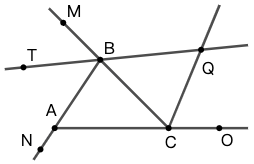
A. 等于 \(\angle{CAN}\) B. 等于 \(\dfrac{\angle{CAN}}{2}\)
C. 等于 \(\dfrac{\angle{CAN}}{3}\) D. 等于 \(\dfrac{\angle{CAN}}{4}\) E. 以上都不对
20 如图 68 所示,在 \(\triangle{ABC}\) 中, \(\angle{A}=50^\circ\) , \(\angle{C}=80^\circ\) 。 \(CP\) 和 \(AR\) 分别是 \(\angle{C}\) 和 \(\angle{A}\) 的角平分线。求 \(\angle{ARC}\) 的度数。
平行线和多边形
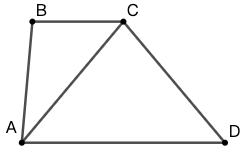
21 图 69 中 \(AD\) 平行于 \(BC\) ,\(AC=CD\) , \(\angle{ABC}=95^\circ\) , \(\angle{BAC}=35^\circ\) 。求 \(\angle{ACD}\) 的度数。
22 图 70 中 \(\angle{\alpha}\) 是锐角,则四边形 \(ABCD\) 的内角和:
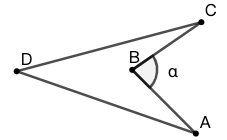
A. 小于 \(180^\circ\) B. 小于 \(360^\circ\)
C. 恰好是 \(360^\circ\) D. 大于 \(360^\circ\)
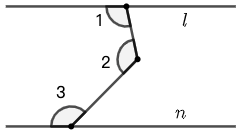
23 在图 71 中, \(l\parallel n\) ,\(\angle{1}=100^\circ\) , \(\angle{2}=120^\circ\) 。求 \(\angle{3}\) 的度数。
24 图 72 中, \(AB\parallel CD\) 。求 \(\angle{E}\) 的度数。
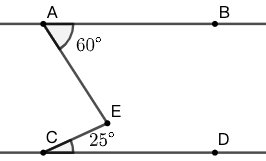
25 图 73 中标记的各个角度之和是多少?
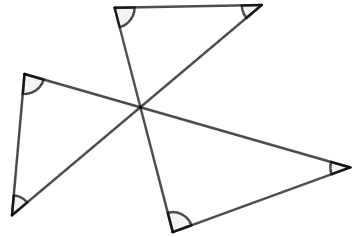
26 在图 74 中, \(\angle{1}=7x+10^\circ\) , \(\angle{5}=3x\) , \(l\parallel m\) 。 \(\angle{2}\) 的度数是多少?
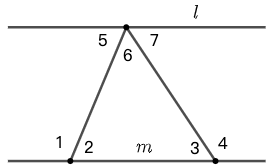
27 在图 75 中,\(l_1\parallel l_2\) ,各角度的数量关系如图所示。求 \(y\) 的值。
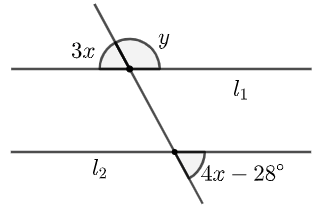
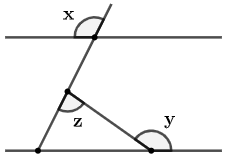
28 在图 76 中, \(l_1\parallel l_2\) ,各角度标注如图所示。 \(\angle{x}\) 的度数是:
A. \(180^\circ-y\) B. \(180^\circ-z\) C. \(180^\circ-z-y\)
D. \(180^\circ+z-y\) E. \(z+y-180^\circ\)
29 图 77 中, \(AE\parallel CD\) , \(B\) 是平行线间一点。 \(\angle{BAE}=100^\circ\) , \(\angle{ABC}=90^\circ\) 。求 \(\angle{BCD}\) 的度数。