数量关系(二)
本章将研究面积相关的数量关系问题。我们将涉及“分数的运算”、“多位数乘法”、“盈亏问题”以及“鸡兔同笼”等主题。
分数
在义务教育课程大纲中,分数的全面引入在五年级上学期,而分数的综合运算则在六年级上学期才讲授。分数的引入,将学生对数学的认识由整数领域引入了有理数领域,这是一次认识飞跃。在学习分数之前,先修的课程会讲解质数和因数分解等概念,这些数学概念会全面用于分数运算。在学习分数之后,你将接触到更加深入的几何和代数知识。
分数的引入有两个意义:
- 分整体为部分的数学表示。这正是汉语“几分之几”的意义所在;
- 整数对除法运算不封闭,引入分数建立有理数域后,除法运算也封闭了。
分数的引入
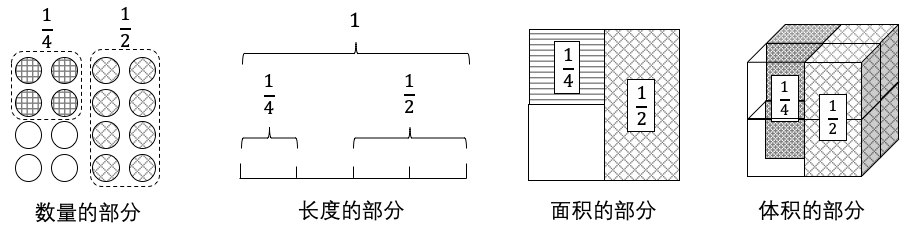
于是很自然地有两个方式引入分数,也有两种方式看待分数符号 \(\dfrac{a}{b}\) :
- 将整体分为 \(b\) 份,取 \(a\) 份(或者将 \(a\) 分为 \(b\) 份);
- \(a\) 除以 \(b\) ;
前者直观,后者更具一般性。这从图 1 与图 中可以看出。
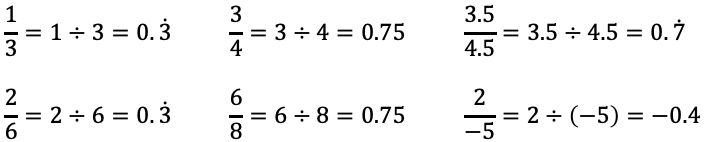
分数的加法
分母相同时,加法很容易。本小节主要关心分母不同的分数之间的加法:
示例: 计算 \(\dfrac{1}{3}+\dfrac{1}{4}\) 。
解: 将整体分为 \(12\) 份,这样既可以 \(3\) 等分,也可以 \(4\) 等分。计算过程如图 3 所示:

☐
上面的示例用长度单位计算分数,用面积计算能更直观地揭示如何取分母的过程,请看如下示例:
示例: 计算 \(\dfrac{1}{3}+\dfrac{1}{4}\) 。
解: 将整体分为 \(12\) 份,这样既可以 \(3\) 等分,也可以 \(4\) 等分。计算过程如图 4 所示:

示例: 计算 \(\dfrac{1}{4}+\dfrac{1}{6}\) 。
分数的乘法
本小节将面积和乘法的定义扩展至分数(有理数域)。
示例: 使用“分整体为部分”的观点计算 \(\dfrac{1}{3}\times\dfrac{1}{4}\) 。

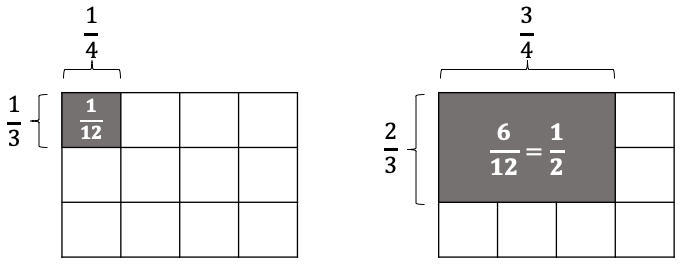
示例: 使用矩形面积计算 \(\dfrac{1}{3}\times\dfrac{1}{4}\) 和 \(\dfrac{2}{3}\times\dfrac{3}{4}\) 。
示例: 计算 \(\dfrac{1}{2}\times\dfrac{1}{3}\) 和 \(\dfrac{1}{3}\times\dfrac{1}{5}\) 。
示例: 计算 \(\dfrac{2}{3}\times\dfrac{1}{2}\) 和 \(\dfrac{2}{3}\times\dfrac{3}{5}\) 。
二项式乘法
示例: 计算 \(12\times13\) 。
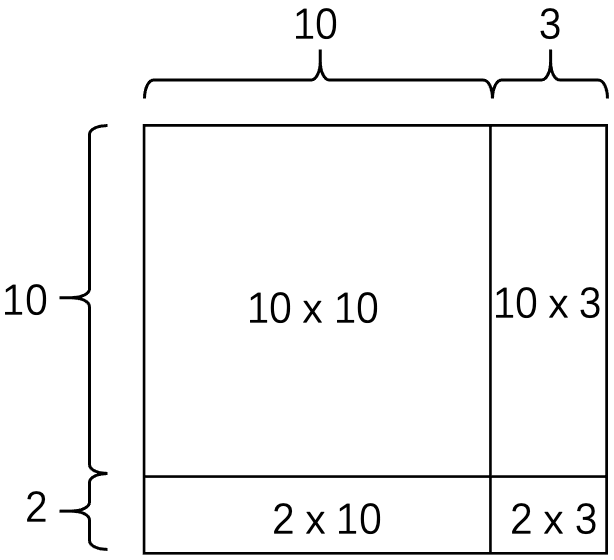
解: 利用乘法分配律,将多位数乘法拆解为个位数乘法: \[\begin{align*} 12\times13&=(10+2)\times(10+3)\\ &=10\times(10+3)+2\times(10+3)\\ &=10\times10+10\times3+2\times10+2\times3\\ &=100+30+20+6\\ &=156 \end{align*}\] \(\square\)
示例: 计算 \(27\times28\) 。
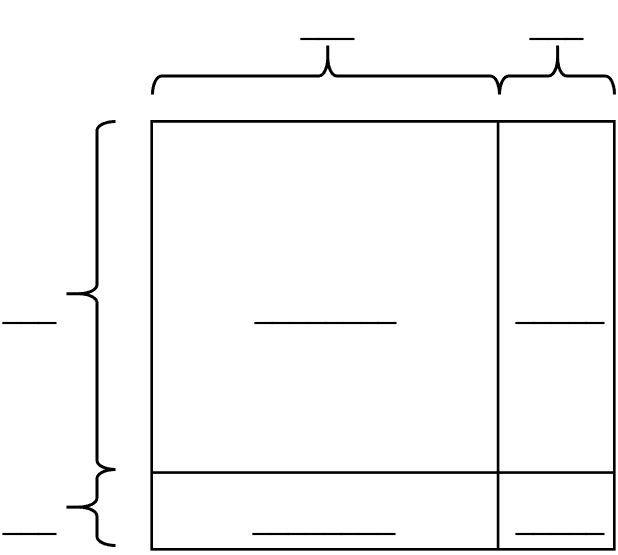
示例: 计算 \(37\times28\) 。

示例: 计算 \(137\times28\) 。
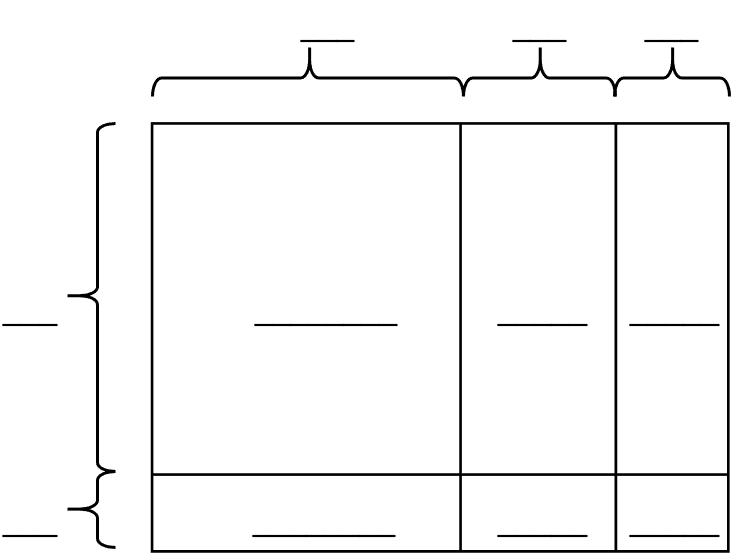
上述诸示例可用代数形式表现为以下一般规律:
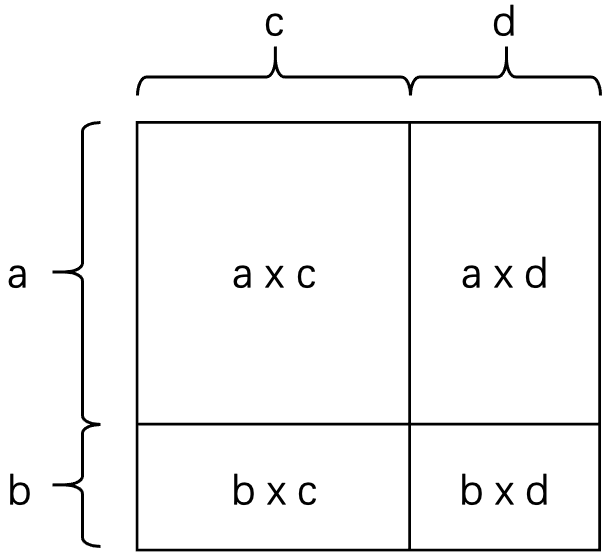
二项式乘法
二项式是只有两项的多项式。一般地,二项式相乘的结果为: \[\begin{align} (a+b)\cdot(c+d)&=a\cdot c + a\cdot b + b\cdot c + b\cdot d \end{align}\]
有一些特殊的二项式乘积结果很有用:
平方和与平方差公式
平方和公式: \[\begin{align} (a+b)\cdot(a+b)&=a^2+2ab+b^2 \end{align}\]
平方差公式: \[\begin{align} (a+b)\cdot(a-b)&=a^2-b^2 \end{align}\]
示例: 推导平方差公式 \((a+b)\cdot(a-b)=a^2-b^2\) 。
示例: 利用平方和公式计算平方表 \(11^2, 12^2, ..., 19^2\) 。
示例: 利用平方表和平方差公式计算 \(12\times14, 12\times16, 12\times18\)
盈亏问题
盈亏问题
盈亏问题是指将一定数量等分,根据剩余(盈)或不足(亏)情况求解数量和等分数的应用题。
盈亏问题最早见于中国的《九章算术》,后来传到亚细亚和欧洲,在欧洲代数学没有发达以前,曾广泛使用书中所载算法达几百年之久,直到1675年,意大利的数学书中还称这方法为la regola del cataino(意为中国算法)。《九章算术》称盈亏问题为原术,书中原文为:“今有(人)共买物,人出八,盈三;人出七,不足四;问人数物价各几何。”这段文字译为今文是:几人共同出钱买东西,每人出 \(8\) 元则多 \(3\) 元,若每人出 \(7\) 元则少 \(4\) 元,求人数和物价。
《盈亏问题》词条
示例: 几人共同出钱买东西,若每人出 \(7\) 元则少 \(4\) 元,每人出 \(8\) 元则多 \(3\) 元,求人数和物价。
解法一 把人数和人均钱数看作长度,其乘积则为矩形面积。如图 12 所示,物价即为 L 形面积。

可以看出,人数所对应的边长为 \(4+3=7\) ,即共有 \(7\) 人。
进一步容易求出物价为 \(7\times7+4=7\times8-3=53\) 元。☐
几何图形为我们提供“从高处俯瞰”数量关系的视角。但我们仍然要继续发展代数能力,当面对复杂的数量关系时,代数手段能够在黑暗中引路。
学习提示
如果你已经熟练掌握上述解法,那么你可以看接下来的方程解法。否则你还是应当先多用算术解法做一些题,然后再用熟悉的题型发展代数能力。
解法二 随便设置一些数值,试着满足一部分条件,然后观察一下没有满足的条件是如何变化的。先简单地假设就 \(1\) 个人。这显然不是题目的答案,但我们可以通过付款条件分别计算一下价格。若每人出 \(7\) 元则少 \(4\) 元,说明价格为 \(11\) 元,而若每人出 \(8\) 元则多 \(3\) 元,说明价格为 \(5\) 元。计算出来的价格不一样,相差 \(6\) 元,说明答案不是 \(1\) 个人。我们再尝试一下 \(2\) 个人,计算出来的价格分别为 \(18\) 和 \(13\) 元,相差 \(5\) 元。继续计算我们会得到表 13 。

计算的目标是让价格差变为 \(0\) ,你应该能够观察到等差数列规律,请推算应当填入表格最后一行的内容,验算并得到最终结论。
解法三 设人数为 \(x\) ,价格为 \(y\) 元 。根据题目条件,可以得到以下方程组:
\[\begin{equation*} \begin{cases} 7x+4=y \qquad\text{每人 7 元少 4 元} \\ 8x-3=y \qquad\text{每人 8 元多 3 元} \end{cases} \end{equation*}\] 用第二个方程减去第一个方程,得到: \[\begin{align*} (8x-3)-(7x+4)&=y-y\\ x-7&=0\\ x&=7 \end{align*}\] 因此共有 \(7\) 人。物价 \(y=7x+4=7\cdot7+4=53\) 元。☐
解法四 设人数为 \(x\) 。根据题目条件可以得到以下方程:
\[\begin{align*} 8x-3&=7x+4\\ x-3&=4\\ x&=7 \end{align*}\] 因此共有 \(7\) 人,物价为 \(7\times7+4=53\) 元。☐
思考与讨论
- 观察图 14 ,该图如何体现盈亏问题的算术求解过程?
- 该图是如何体现盈亏问题的方程组求解过程的?

鸡兔同笼问题
鸡兔同笼问题
鸡兔同笼是中国古代的数学名题之一,其本质是二元一次方程组问题。《孙子算经》(距今约1500年)中就记载了这个有趣的问题。书中是这样叙述的:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
示例: 鸡和兔共 \(35\) 只,共有腿 \(94\) 条。求鸡和兔各几只?
在上一节“盈亏问题”中发展出的各种方法都可以用来求解本题。
解法一 某种动物的总腿数等于头数乘以单只的腿数,我们可以用矩形面积来表示乘法的结果。于是题目等同于:
在长度为 \(35\) 的线段 \(AB\) 上找一点 \(C\) ,分别做 \(AC\times2\) 和 \(BC\times4\) 的矩形,所得图形的面积为 \(94\) 。

☐
验算过程:
思考与讨论
- 你应当如何写验算过程?
- 传统的“假设抬腿法”和上面解法的几何图形是如何对应的?
- 如果“假设都是兔子”再反求鸡的数目,应该如何画图?
解法二 题目有两个条件“共 \(35\) 只”和“共 \(94\) 条腿”。我们先尝试着满足第一个条件:假设 \(35\) 只动物都是鸡,没有兔子。这显然无法满足第二个条件,因为腿总共只有 \(70\) 条。于是我们要把一些鸡换成兔子。每次将 \(1\) 只鸡换成兔子,腿会增加两只。不断增加兔子的过程如表 16 所示:

我们只要找到标记问号的一行应该填入什么数字即可。于是问题转换为:
\(1\) 只兔子,腿 \(72\) 。每次增加 \(1\) 只兔子,增加两条腿。多少只兔子时,腿有 \(94\) 条?
这是一个已知等差数列首项、公差和末项,求项数的问题:项数等于末项减首项,除以公差再加一
即:已知 \(a_1=72, \quad d=2, \quad a_n=94\) , 求 \(n\) 。 \[n=\dfrac{a_n-a_1}{2}+1=\dfrac{94-72}{2}+1=12\]
因此我们知道有 \(23\) 只鸡 \(12\) 只兔子。
验算:将 \(3\) 和 \(7\) 代入题意:\(3\times2+7\times4=34\) ,相符。☐
解法三 设鸡 \(x\) 只,兔 \(y\) 只。根据题目条件可以列出以下方程组:
百僧百馍问题
百僧百馍问题
百僧百馍问题是我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”
示例: 有一百个和尚分一百个馒头,大和尚每人三个馒头,小和尚每三人一个馒头,馒头正好分完。请问大小和尚各有几人?
分析 这个问题说穿了就是鸡兔同笼的分数版本:“鸡兔共有 \(100\) 只,每只鸡 \(\dfrac{1}{3}\) 条腿,每只兔 \(3\) 条腿。问鸡兔各几只?”。或者直接使用分数运算,或者把分数凑整。只要把所有的馒头数(腿数)都乘以三,我们就可以避免分数运算:
“一百个和尚分三百个馒头,大和尚每人九个馒头,小和尚每人一个馒头,馒头正好分完。请问大小和尚各有几人?”
请读者自行补充求解过程:
解法一
解法二
解法三
随堂练习
练习: 计算 \(\dfrac{1}{2}+\dfrac{1}{3}\),\(\dfrac{1}{2}+\dfrac{1}{4}\),\(\dfrac{1}{2}+\dfrac{1}{5}\),\(\dfrac{1}{2}+\dfrac{1}{6}\)
练习: 计算 \(\dfrac{1}{3}+\dfrac{1}{4}\),\(\dfrac{1}{3}+\dfrac{1}{5}\),\(\dfrac{1}{3}+\dfrac{1}{6}\)
练习: 计算 \(\dfrac{1}{4}+\dfrac{1}{5}\),\(\dfrac{1}{4}+\dfrac{1}{6}\),\(\dfrac{1}{5}+\dfrac{1}{6}\)
练习: 计算 \(\dfrac{2}{3}+\dfrac{1}{3}\),\(\dfrac{2}{3}+\dfrac{1}{4}\),\(\dfrac{2}{3}+\dfrac{1}{5}\),\(\dfrac{2}{3}+\dfrac{1}{6}\)
练习: 计算 \(\dfrac{3}{4}+\dfrac{1}{4}\),\(\dfrac{3}{4}+\dfrac{1}{5}\),\(\dfrac{3}{4}+\dfrac{1}{6}\)
练习: 计算 \(\dfrac{1}{2}\times\dfrac{1}{2}\),\(\dfrac{1}{3}\times\dfrac{1}{3}\),\(\dfrac{1}{4}\times\dfrac{1}{4}\)
练习: 计算 \(\dfrac{1}{2}\times\dfrac{1}{3}\),\(\dfrac{1}{2}\times\dfrac{1}{4}\),\(\dfrac{1}{2}\times\dfrac{1}{5}\),\(\dfrac{1}{2}\times\dfrac{1}{6}\)
练习: 计算 \(\dfrac{1}{2}\times\dfrac{2}{3}\),\(\dfrac{1}{2}\times\dfrac{2}{4}\),\(\dfrac{1}{2}\times\dfrac{2}{5}\),\(\dfrac{1}{2}\times\dfrac{2}{6}\)
练习: 计算 \(\dfrac{1}{2}\times\dfrac{2}{3}\),\(\dfrac{1}{2}\times\dfrac{2}{4}\),\(\dfrac{1}{2}\times\dfrac{2}{5}\),\(\dfrac{1}{2}\times\dfrac{2}{6}\)
练习: 计算 \(\dfrac{2}{3}\times\dfrac{3}{4}\),\(\dfrac{3}{5}\times\dfrac{2}{3}\),\(\dfrac{3}{4}\times\dfrac{2}{5}\)
练习: 有一根木棍上有三种刻度,第一种刻度将木棍 \(10\) 等分,第二种刻度将木棍 \(12\) 等分,第三种刻度将木棍 \(15\) 等分。如果沿每条刻度线将木棍锯断,请问木棍共被锯成多少段?
练习: 几人共同出钱买东西,若每人出 \(6\) 元则少 \(4\) 元,每人出 \(8\) 元则多 \(10\) 元,求人数和物价。
某田径队共有 \(10\) 名选手(其中有九名普通队员和一名队长)参加全国运动会比赛获得冠军,校长颁发每位普通队员 \(1500\) 元奖金,队长则比全队 \(10\) 名选手所获得的平均奖金还多 \(900\) 元。请问队长所获得的奖金为多少元?
某电视机厂每天生产电视 \(500\) 台,在质量评比中,每生产一台合格电视机记 \(5\) 分,每生产一台不合格电视机扣 \(18\) 分。如果四天得了 \(9931\) 分,那么这四天生产了多少台合格电视机?
\(5\) 角和 \(1\) 元的硬币共 \(36\) 枚,币值共 \(22.5\) 元。两种硬币各多少枚?
家聪、小明、佳莉三人出同样多的钱买了同一种铅笔若干支,家聪和小明都比佳莉多拿 \(6\) 支,他们每人给佳莉 \(28\) 元,请问铅笔每支的价钱是多少元?
某小学去年增加 \(5\) 个班级后每班平均人数减少 \(5\) 人,今年再增加 \(5\) 个班级,每班平均人数又减少 \(4\) 人。假设去年与今年学生总人数不变,请问该小学现共有学生多少人?
甲、乙两人合伙开设一家公司,甲的股份是乙的 \(1.5\) 倍。现有丙欲入股此公司,三人协议由丙拿出 \(1500\) 万元购买甲乙二人的部分股份,使得三人的股份都各占三分之一。请问甲卖给丙的股份对价多少万元?