数量关系（一）

“柏拉图在雅典近郊创办了一个讲学的场所，定名‘学园’…后世‘学院’一词即由此而来。他重视数学，强调数学在训练智力方面的作用，主张通过几何的学习培养逻辑思维能力，将抽象的逻辑规律体现于几何图形之中。”

本章我们来考虑一类问题：根据数量间的关系求数量本身。这类问题往往体现为“和差问题”、“和倍问题”或者“差倍”。在小学中年级阶段，我们往往使用几何化的手段探求数量关系。几何化的手段直观地揭示了求解的计算过程。在数学学习的各个阶段，都应当重视几何化手段的运用。

和差问题

和差问题 (Sums and Difference) 是指已知两个数量的和与差，求两个数量的应用题。

和差问题的几何作图

示例：给定一长一短两条线段。将较长线段分为两部分，使得两部分长度之差等于较短线段。

动画和差问题的尺规作图

作图不妨设较短线段为 $AB$ 较长线段为 $CD$ ，如图 2 所示。

[(1)] 在 $CD$ 上截取一点 $E$ ，使得 $CE=AB$ ，如图 2 (1) 所示。
[(2)] 以 $DE$ 为半径，分别以 $D$ 和 $E$ 为圆心做圆，交于 $M,N$ 两点，如图 2 (2) 所示。
[(3)] 连接 $MN$ ，交 $DE$ 于点 $F$ ，则 $F$ 为 $DE$ 的中点。

$CF$ 和 $FD$ 即为所求的两部分， $CF-FD=AB$ 。

☐

和差问题的作图过程

示例：给定一大一小两个角。将较大的角分为两部分，使得两部分角度之差等于较小的角。

动画和差问题（角）作图

作图设给定的两个角如图 4 (1) 所示，命名为 $\angle{A}$ 和 $\angle{B}$。

[(1)] 分别以 $A,B$ 为圆心，任意相等半径做圆，交 $\angle{A}$ 的边于 $C,D$ ，交 $\angle{B}$ 的边于 $E,F$ ，如图 2 (1) 所示。
[(2)] 以 $EF$ 为半径，以 $D$ 为圆心做圆，在 $\angle{A}$ 的内部交圆 $A$ 于 $G$ 。连接 $AG$ ，有 $\angle{DAG}=\angle{B}$。如图 2 (2) 所示。（做角等于已知角）
[(3)] 做 $\angle{CAG}$ 的角平分线 $AH$ ，如图 2 (3) 所示。

$AH$ 将 $\angle{A}$ 分成了所要求的两部分。 $\square$

和差问题（角）作图

和差问题的算术解法

前一小节的几何作图已经给出了和差问题的直观解释。本节将完整地讨论和差问题的各种求解方法。

示例：你有黑色和白色棋子共 $20$ 个，黑色棋子比白色棋子多 $4$ 个。问黑白棋子各有多少个？

解法一 （线段图方法）我们用前一小节的几何提法重新描述本题目：“将长度为 $20$ 的线段分为两段，其中较长的一段比较短的那段长 $4$ ”。

求解黑白棋子问题的线段图

于是我们可以立刻作图得到问题的解。如图 5 所示，线段 $AC$ 和线段 $BC$ 的长度就是符合题目中数量关系的解。换成黑白棋子就是黑色棋子 $12$ 个，白色棋子 $8$ 个。

☐

线段图是小学数学中最喜欢使用的手段。线段图能很直观地解决许多通常我们使用方程解决的问题。小学中高年级的学生应当熟练掌握这种方法。

思考与讨论

你应该如何写计算过程呢？如何描述计算过程每步的结果？
传统的课外数学课程，喜欢用如图 6 所示的线段图。请比较和，你更喜欢哪一个？

线段图表示的数量关系

♣ 如果你对和差问题还不是很熟悉，跳过本节其它内容，复习一下，然后去看下节的和倍问题。

解法二 （列表规律法）既然是棋子的数目，那么只能 $0$ 个或更多。两个数的和是 $20$ ，那么只有可能 $0+20$, $1+19$, $2+18$, … , $19+1$, $20+0$ 这 21 种情况。

用数数来求解和差问题

在这些情况中，找到符合黑色比白色多 $4$ 个的那一组就好。于是答案是 $12+8$ ，即黑色棋子是 $12$ 个，白色棋子是 $8$ 个。

☐

这个解法的优势是不需要使用更高级的数学知识，你只需要使用加法就可以。缺点是当两个数量的和很大时，比如 $1000$ ，你就要试很多次。

这种解法的另一个价值是可以配合坐标系来解释等差数列和线性方程组的几何意义。我们将在以后的课程中讲到这一点。

解法三 （先等分再调整）我们注意到这样一个事实：如果棋子数目一样多，将 $1$ 颗白色棋子涂黑会导致黑色棋子多出 $2$ 个，将 $2$ 颗白色棋子涂黑会导致黑色棋子多出 $4$ 个.

先等分再调整

所以在黑白棋子各 $10$ 枚的情况下，涂黑 $2$ 枚白色棋子，就能够满足黑色棋子多 $4$ 枚的条件。因此黑色棋子有 $12$ 枚，白色棋子有 $8$ 枚。

☐

说良心话，这是笔者在上小学时最喜欢的解法。笔者喜欢在头脑中先“调整棋子数目”，得到正确结论后，再按照老师要求的方法写出“解题步骤”。

思考与讨论

你应该如何写计算过程呢？你如何描述计算过程每一步的结果呢？
和上述解法对应的几何问题和尺规作图过程是什么样子呢？

♣ 请注意，解法三体现了和差问题的一个重要模型：两个数量保持和不变，其中一个量“给”另一个量某个“小量”，则二者差的变化是两倍的“小量”。笔者的教学实践表明，对初次接触该问题的小学中年级同学来说，这并不是显然的，需要反复体会。为了更好地理解该模型，我们来看一道相关的几何题目。

示例：¹ 如图 9 所示，在 $\triangle{ABC}$ 中， $D$ 是 $AC$ 上一点， $AB=AD$ ， $\angle{CAB}-\angle{ABC}=30^\circ$ 。求 $\angle{CBD}$ 的度数。

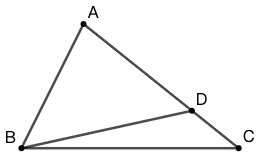
分析把三角形拆开，如图 10 所示。我们把除 $\angle{A}$ 之外的角称为“底角”。两个三角形有一个角重叠，又因为三角形的内角和恒为 $180^\circ$ ，所以不论如何变化，另外两个角之和都是 $180^\circ-\angle{A}$ 。

可以看出，$\triangle{ABD}$ 到 $\triangle{ABC}$ 的变化过程中，底角的和不变，底角的差增加了 $30^\circ$ 。于是我们知道 $\angle{B}$ 增加了差的一半 $15^\circ$ ，也就是 $\angle{CBD}=15^\circ$ 。

☐

xxx

♣ “和差问题”并不仅仅是算个小球、糖块、零钱、年龄那种“奥数练习册”问题，它是一种很广泛普遍的模型。

和差问题的方程解法（四年级选学）

如果你还没有对和差问题的算术解法融会贯通，就不要看这一节。将来我们学到《方程》这一主题时，还会再回来学。

方程

方程 (equations) 是含有未知量的等式。将题目中的未知量用字母标记，根据条件列出等式。通过一些简单的变换规则，就可以得到未知量的值

对于和差问题这类题目来说，方程解法显得“舍近求远”。然而利用方程进行求解目的实在是要开始引导学生逐渐理解并掌握这一强大的手段。

解法三 设未知量、列方程、解方程。用 $a$ 代表白色棋子的数目，那么黑色棋子的数目就是 $a+4$ 。两种棋子一共 $20$ 枚，也就是： \[\begin{align} a+a+4&=20 \qquad\text{等号两边}+4 \notag \\ a + a&=16 \qquad\text{等号两边}\div2 \notag\\ a&=8 \notag \end{align}\] 因此白色棋子有 $12$ 枚，黑色棋子有 $8+4=12$ 枚。

☐

解法三就是解法一的代数表示。我们凭借代数记号可以写出很简练明确的数学推导过程。我们也可以用两个字母分别表示黑白棋子的数目，列出两个方程，如解法四所示：

解法四 用 $x$ 代表黑色棋子的数目， $y$ 代表白色棋子的数目。可以列出以下方程：

\[\begin{equation*} \begin{cases} x+y=20 \qquad\text{黑白棋子总数是 $20$ 枚} \\ x-y=4 \qquad\text{黑色棋子比白色棋子多 $4$ 枚} \end{cases} \end{equation*}\]

方程的解法如图 11 所示：

求解方程

求出黑色棋子有 $12$ 颗，进一步可以求得白色棋子有 $8$ 颗。

☐

关于列方程解决问题的一般方法，以及方程的几何意义，并不是本章的中点，我们会另辟章节讲述。

代数描述和求解公式（四年级选学）

$x,y$ 表示未知量，$d$ 表示差 (difference) ，

和差问题的代数描述和求解公式

已知 $x,y$ 的和 $x+y=S$ ，其差 $x-y=d$ ，则 $x,y$ 分别为： \[\begin{equation} x=\dfrac{S+d}{2}\quad ,\quad y=\dfrac{S-d}{2} \end{equation}\]

思考与讨论

如何判断上述公式的正确性呢？
如何推导出上述公式呢？

几何观点

用线段图推导和差问题求解公式

代数观点

将上述两个等式的左右两侧分别相加，得到新的等式： \[2x=S+d\]

从而得到： \[x=\dfrac{S+d}{2}\]

思考与讨论

你能用类似的方法计算 $y$ 么？
在上述推导中运用了哪些基本法则？

稍微复杂的和差问题

和差问题有一些变种，学习这些问题的重要目的是锻炼阅读理解能力，进一步掌握把文字转换为数学模型的能力。

间接地给出和差条件

示例：² Alex 和 Besty 一共有 $150$ 元零花钱。如果 Alex 消费 $13$ 元并且 Besty 消费 $27$ 元，他们将剩下相同的钱。请问 Alex 有多少钱？

示例：³ Alex 和 Besty 各有若干钱。如果 Alex 给 Besty $12$ 元钱，他就比 Besty 少 $6$ 元钱。问 Alex 比 Betsy 多几元钱？

涉及三个量的和差关系

示例：⁴ Alex 、 Bob 和 Cathy 一起加工了 $420$ 个零件。 Alex 比 Bob 多加工 $10$ 个， Bob 比 Cathy 少加工 $17$ 个。问每个人分别加工了多少零件？

涉及物理、几何或其它常识

示例：⁵ 船顺流而下时，每小时行驶 $68$ 千米，逆流而上时每小时 $56$ 千米。请问船在静水中的时速是多少？

示例：⁶ 两个自行车运动员 Alex 和 Bob 进行训练。如果二人从 $56$ 英里的赛道两端相向骑行， $8$ 小时相遇。如果二人同时从一端出发，在骑行 $6$ 小时后， Alex 领先 $6$ 英里。求二人的时速分别是多少？

示例：⁷ 矩形的长比宽多 $11cm$ ，周长为 $118cm$ 。该矩形的长是多少？

示例： $\angle{A}$ 的补角和余角之和等于平角的度数，求 $\angle{A}$ 的度数。

和倍问题

和倍问题 (Sums and Multipliers) 是指已知两个数量之和及倍数关系，求解两个数量的应用题。

和倍问题的几何作图

示例：给定一个正整数 $m$ ，将给定线段分成两部分，使得其中一段是另一段的 $m$ 倍。

动画三等分线段的作图

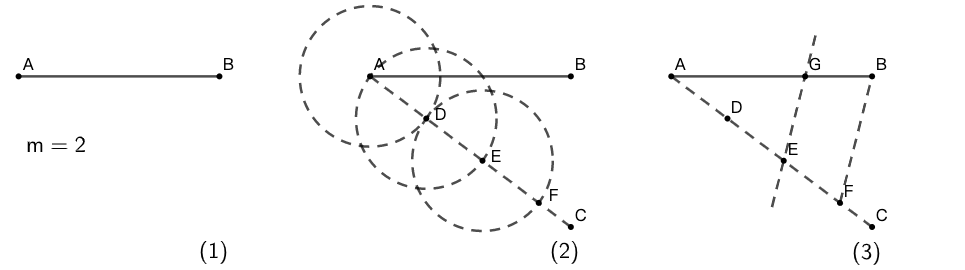
作图设给定线段为 $AB$ ，出于简单起见，令 $m=2$ 。（作图过程可以很容易推广至更大的 $m$ ）

[(1)] 在直线 $AB$ 外找一点 $C$ ，做直线 $AC$ 。
[(2)] 在直线 $AC$ 上任取一点 $D$ ，构建 $AD=DE=EF$ ，图 14 (2) 。
[(3)] 连接 $BF$ ，过 $E$ 做 $BF$ 的平行线交 $AB$ 于点 $G$ ，图 14 (3) 。 9 点 $G$ 将 $AB$ 分为所求的两部分， $AG=2BG$ 。
☐

xxx

以上作图过程用到了以下重要性质：

平行线分线段成比例 (Euclid VI.2)

如果一条直线平行于三角形的一条边，那么它所截得的边成比例；（逆命题也成立）如果三角形的边被截成比例，那么通过两点的直线平行于三角形的第三边。

这是一个很靠后的性质，在《几何原本》要等到第六卷，在课内则要到初中再学，也不见于现在市面上的各种小学奥数教材。等稍后我们学了三角形面积后就可以证明它，此处先按下不表，你从直观上认识到上述作图的正确性就可以。

示例：（选学）将给定角分成两部分，使得其中一个角的度数是另一角的 $2$ 倍。

分析这实际上就是要做一个角等于给定角的 $\dfrac{1}{3}$ ，这就是著名的三大尺规作图难题之一：三等分角。单纯使用没有刻度的直尺和圆规是无法将任意角三等分的。至于其中的道理，需要等你初中学了无理数才能理解。古希腊数学家阿基米德在直尺上做了一个刻度（这超出了传统尺规作图的限制），解决了三等分任意角的问题。

三等分角

作图设给定角为 $\angle{AOB}$ 。在直尺上标记两个点 $M,N$ 得到一段固定长度 $MN$ 。

动画三等分角的演示

[(1)] 以点 $O$ 为圆心，长度 $MN$ 为半径做圆，交射线 $OA$ 于点 $C$ 。
[(2)] 让直尺过 $C$ 点，再将直尺的 $M$ 点至于圆上滑动，当 $N$ 落在 $OB$ 所在直线上时，过 $C,M,N$ 做直线。如图 15 所示。此时则 $\angle{ONC}=\dfrac{1}{3}\angle{AOB}$ 。（证明留作思考题）
[(3)] 过点 $O$ 做 $OD$ 平行于 $CN$ ，如图 15 所示。

$OD$ 将 $\angle{AOB}$ 分为所求的两部分，其中 $\angle{AOD}=2\angle{BOD}$ 。

☐

思考与讨论

拿尺子和圆规完成上述作图过程，并且使用量角器验证一下你是否得到了三等分角。
证明上述作图过程的正确性。（提示：连接辅助线 $OM$）

三等分角的证明辅助线

和倍问题的数量计算

同和差问题一样，和倍问题也有很多变形。有些是以隐含的方式给出条件，有些则更加复杂。

示例：黄色和红色弹珠共 $95$ 个。黄色弹珠的数目是红色的 $4$ 倍。问黄色和红色弹珠各有多少个？

示例：将平角分为两个角，其中一个的度数是另一个的两倍。

示例：一个角的度数是其余角的两倍，求该角的度数。

示例：（作图题）给定一长一短两条线段，将较长线段分为两段，其中一段的长度是另一段的两倍还多较短那条线段。

动画和差倍问题作图

稍微复杂的和倍问题

实际的题目不会那么直接地告诉你和倍关系，你需要稍微处理一下题目的条件。你需要通过清晰的思考或作图探求数量关系。

示例：⁸ 学校里共有男孩和女孩 $786$ 人。如果男孩的人数减少 $40$ ，女孩的人数增加 $10$ ，男孩的人数就是女孩的 $3$ 倍。问男孩和女孩实际各多少人？

示例：⁹ 再过 $10$ 年， Mark 的爸爸就比 Mark 的年龄的两倍小两岁。 Mark 和他爸爸现在的年龄之和是 $41$ 岁。现在 Mark 和他爸爸的年龄分别是多少？

有的时候，题目会反过来问，如下题：

示例：¹⁰ 红色的珠子有 $140$ 颗，蓝色的珠子有 $180$ 颗。为了让红色的珠子是蓝色珠子的 $3$ 倍，需要把多少颗蓝色珠子涂成红色？

你还会遇到三个数量的和倍问题：

示例：¹¹ 农场主 John 种了 $840$ 棵树，其中有苹果树、梨树和桃树。梨树的数目是桃树的 $2$ 倍。苹果树的数目是桃树的 $3$ 倍。请问 John 每种树各种了几棵？

甚至四个数量：

示例：¹² 将 $108$ 名学生分为 $4$ 组，使得第 $1$ 组学生人数的 $2$ 倍：

是第 $2$ 组学生人数的一半；
比第 $3$ 组学生少 $2$ 人；
比第 $4$ 组学生多 $2$ 人。

问每组学生各几人？

当然你还要注意审题（条件和问题）：

示例：¹³ 某个长方形的周长是 $22$ ，它的长度比宽度的三倍少 $5$ 。该长方形的面积是多少？

差倍问题

差倍问题 (Difference and Multipliers) 是指已知两个数量之差及倍数关系，求解两个数量的应用题。

差倍问题的一个典型题目如下所示：

示例：¹⁴ Alex 拥有的弹珠数目是 Bob 的 $3$ 倍。如果 Alex 比 Bob 多 $80$ 个弹珠，那么二人各拥有多少个弹珠？

差倍问题的几何作图

示例：给定一条线段 $AB$ ，在 $AB$ 的延长线上找一点 $C$ 使得 $AC=3BC$ 。

差倍问题的几何作图

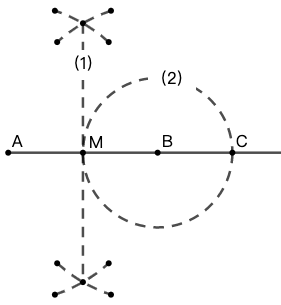
作图本题目的“差”条件是隐含给出的：$AC-BC=AC$

[(1)] 做线段 $AB$ 的中点 $M$ 。
[(2)] 在线段 $AB$ 的延长线上取点 $C$ 使得 $BC=BM$ 。

点 $C$ 即为所求的点。

与和倍问题类似，差倍问题只需要把“差”分为“倍数$-1$”部分，就可以获得较小的那个数值。

示例：给定一条线段 $AB$ ，在 $AB$ 的延长线上找一点 $C$ 使得 $AC=4BC$ 。

差倍问题的数量计算

示例：¹⁵ 农场主约翰收获的苹果比香蕉多 $15$ 箱。又知道苹果是香蕉的 $4$ 倍多 $3$ 箱。请问两种水果各有多少箱？

示例： $\angle{A}$ 补角的度数是余角的 $6$ 倍，求 $\angle{A}$ 的度数。

示例：¹⁶ 孙家有七位姐妹，她们的年龄都不同且相邻两姐妹都相差两岁。已知大姐今年的年龄是最小妹妹的 $3$ 倍，请问大姐今年几岁？

示例：姐姐比妹妹大 $6$ 岁，今年姐姐是妹妹年龄的四倍。几年之后姐姐是妹妹年龄的两倍？

分数表示的倍数关系

在我们学习过分数之后，就可以使用分数来表示倍数关系了。

示例：在给定线段 $AB$ 上找一点 $C$ ，使得$BC=\dfrac{1}{3}AC$ 。

分析处理“几分之一”这种问题无新奇之处，因为这等同于整数倍数的和倍问题：$AC=3BC$ 。请读者自行完成作图：

我们更加关心的是那些分子不为 $1$ 的分数，请看如下示例：

示例：在给定线段 $AB$ 上找一点 $C$ ，使得$BC=\dfrac{2}{3}AC$ 。

作图先用整数构建 $\dfrac{2}{3}$ 的数量关系，再利用平行线分线段 $AB$ 。

[(1)] 过点 $A$ 做射线，从 $A$ 开始截取五段相等的连续线段。如图 20-(1) 所示，取点 $D,E$ 。有 $DE=\dfrac{2}{3}AD$ 。
[(2)] 过点 $D$ 做 $BE$ 的平行线，交 $AB$ 与点 $C$，如图 20-(1) 所示。

点 $C$ 即为所求的点。

☐

分数和倍问题

小学中年级的同学只学了“分数的概念”，尚未学到“分数的运算”，更未学到“比例”。通过使用整数构建分数的倍数关系，学习者能够更深入地理解分数的概念，为将来的学习打下基础。另外，通过整数构建分数比例，也往往是人们在头脑中处理简单分数问题的便捷方法。为了更好地说明这一点，请看如下示例：

示例：盒子里共 20 枚黑白棋子，白色棋子数目是黑色的 $\dfrac{2}{3}$ 。请问黑白棋子各多少枚？

解：用整数 $2$ 和 $3$ 构建 $\dfrac{2}{3}$ 的倍数关系：$2$ 是 $3$ 的 $\dfrac{2}{3}$ 。将 $20$ 枚棋子分为 $5$ 份，其中 $3$ 份是黑色，另外 $2$ 份是白色，如图 21 所示。

分数和倍问题

因此得出黑色棋子有 $12$ 枚，白色棋子有 $8$ 枚。

☐

在处理分数倍数的问题时，找到两个小整数来体现这种关系，是解决问题的突破口

分数倍数不但体现在和倍问题中，也可以体现在差倍问题的倍数关系上。请看如下两个示例：

示例：盒子里的黑色棋子数目比白色棋子多 $20$ 枚，白色棋子数目是黑色的 $\dfrac{2}{3}$ 。请问黑白棋子各多少枚？

示例： $\angle{A}$ 的补角是余角的两倍半，求 $\angle{A}$ 的度数。

和差问题

练习：¹⁷ 希望小学三四年级的学生总人数是 $260$ 。如果三年级的学生比四年级学生少 $30$ 人，那么两个年级各有多少人？

练习：¹⁸ Alex 和 Besty 一共有 $150$ 元零花钱。如果 Alex 再存 $13$ 元而 Betsy 消费 $27$ 元，他们将拥有相同数量的钱。请问 Alex 有多少钱？

练习：¹⁹ Alex 和 Besty 一共有 $100$ 元零花钱。如果 Alex 给 Betsy $12$ 元，那么 Alex 就比 Betsy 多 $6$ 元钱。请问原先两人各有多少钱？

和倍问题

练习：²⁰ 数学俱乐部里男孩和女孩共 30 人。男孩比女孩的两倍多 3 人。请问男孩和女孩各多少人？

练习：²¹ 男孩和女孩共有 $200$ 人。男孩的人数比女孩的 $3$ 倍少 $16$ 人。问男孩和女孩各多少人？

练习：²² Alex 和 Bob 共有 $998$ 美元。 Alex 的钱比 Bob 的两倍少 $238$ 元。二人各有多少钱？

练习：²³ 学校里共有男生女生 $786$ 名。如果男生数量增加 $40$ ，女生数量减少 $10$ , 那么男生人数就是女生人数的三倍。问男生女生各有多少人？

差倍问题

练习：²⁴ 农场主约翰养的白兔子和灰兔子。白兔子比灰兔子多 $32$ 只，数量是灰兔子的 $5$ 倍。约翰养了多少只白兔子？

练习：²⁵ Alex 和 Bob 各有一些弹珠。 Alex 的弹珠数目是 Bob 的 $3$ 倍。如果 Alex 减少 $260$ 个弹珠而 Bob 减少 $60$ 个弹珠，两人的弹珠就一样多。请问二人各有多少弹珠？

练习：有 $A,B$ 两个数，已知 $A+B=540$ 且 $A-B=30$ ，求 $A,B$ 的值。

²⁶ 长方形的周长是 $144$ 米。它的宽度比长度少 $4$ 米。长方形的面积是多少？

在 $\triangle{ABC}$ 中， $\angle{A}=2\angle{C}$ ， $\angle{B}=3\angle{C}$ 。请计算 $\triangle{ABC}$ 各个内角的度数，并以 $3cm$ 为 $AC$ 的长度绘制该三角形。

²⁷ 小丁在 $16$ 岁生日那天（年龄为 $16$ 岁）向爸爸要求购买一辆摩托车作为生日礼物。爸爸回答说：“不行，等我的年龄是你的三倍时，我才会买给你。”爸爸现年 $52$ 岁，请问再过几年小丁才能得到爸爸买给他的摩托车？

²⁸ 汽车以每小时 $10km$ 的匀速上山，以每小时 $50km$ 的匀速下山，汽车到山顶后立即以原路下山，共费时 $4$ 小时。请问汽车上山共行驶多长时间？

在直角三角形 $\triangle{ABC}$ 中， $\angle{A}$ 是 $\angle{B}$ 的两倍。请画出 $\triangle{ABC}$ 的所有可能形状，并标注角度。

²⁹ Alex 和 Bob 在一段 $72$ 公里的道路上骑行。如果两人两端同时出发，相向而行， $9$ 小时后相遇。如果两人从道路一端同时出发， $8$ 小时后 Alex 领先 Bob 16 公里。请问二人骑行的时速是多少？（假定二人速度不变）

有 $A,B$ 两个数，已知 $A+B=540$ 且 $A=4\cdot B$ ，求 $A,B$ 的值。

有 $A,B$ 两个数，已知 $A-B=540$ 且 $A=4\cdot B$ ，求 $A,B$ 的值。

³⁰ 在教室里共有 $36$ 位学生，其中男学生与女学生的人数比为 $3:1$ 。请问再加入多少位女同学就可以使教室内男学生与女学生的人数比成为 $9:5$ ？

³¹ 四位小朋友合购一个价值 $600$ 元的生日礼物送给同学。第一位小朋友付的钱是其他小朋友付的总数的 $\dfrac{1}{3}$ ，第二位小朋友付的钱是其他小朋友付的总数的 $\dfrac{1}{4}$ ，第三位小朋友付的钱是其他小朋友付的总数的 $\dfrac{1}{5}$ 。请问第四位小朋友付了多少钱？

³² 欧几里得《几何原本 (Elements) 》是希腊几何学的重要著作，它于明朝随着意大利传教士利玛窦 (Matteo Ricci) 传入中国。徐光启与利玛窦两人共同翻译《几何原本》，于公元 1607 年译完前六卷。徐光启在 1629 年督修新历法，但尚未完成就去世了，最后这部历法于 1634 年才由李天经完成。已知徐光启逝世时的年龄是他出生时公元年份的 $\dfrac{1}{2}$ ，请问徐光启在世多少年？

³³ 农场主 A、B、C 三人各有牲畜若干。一天三人在酒吧闲聊：

A 对 B 说：“如果我以 $6$ 只猪与您交换 $1$ 匹马，则您的牲畜数量是我的 $2$ 倍。”

C 对 A 说：“如果我以 $14$ 只羊与您交换 $1$ 匹马，则您的牲畜数量是我的 $3$ 倍。”

B 对 C 说：“如果我以 $4$ 只牛与您交换 $1$ 匹马，则您的牲畜数量是我的 $6$ 倍。”

请问三位农场主各有多少只牲畜？

³⁴ 汽车以每小时 $30km$ 的匀速上山，以每小时 $50km$ 的匀速下山，汽车到山顶后立即以原路下山，共费时 $4$ 小时。请问汽车上山共行驶多少 $km$ ？

和差问题（一）

甲乙二人共有 $10$ 个球，将球平均分给两人，每人有 $\_\_\_\_$ 个球。

甲乙二人各有 $5$ 个球，甲给乙 $1$ 个球后，甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙少 $\_\_\_\_$ 个球。

甲乙二人共有 $10$ 个球，将球平均分给两人，然后甲给乙 $1$ 个球，甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙少 $\_\_\_\_$ 个球。

将 $100$ 个球平均分给甲乙二人，然后甲给乙 $1$ 个球，甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙少 $\_\_\_\_$ 个球。

将 $100$ 个球平均分给甲乙二人，然后甲给乙 $\_\_\_\_$ 个球，甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙少 $4$ 个球。

将 $100$ 个球平均分给甲乙二人，然后甲给乙 $\_\_\_\_$ 个球，甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙少 $6$ 个球。

将 $100$ 个球平均分给甲乙二人，然后甲给乙 $\_\_\_\_$ 个球，甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙少 $8$ 个球。

将 $100$ 个球平均分给甲乙二人，然后甲给乙 $\_\_\_\_$ 个球，甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙少 $10$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $2$ 个球。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $4$ 个球。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $6$ 个球。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $8$ 个球。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $10$ 个球。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

和差问题（二）

甲乙二人共有 $11$ 个球，拿出 $1$ 个球，将剩下的球平均分给两人，每人有 $\_\_\_\_$ 个球。

甲乙二人共有 $11$ 个球，拿出 $1$ 个球，将剩下的球平均分给两人，再把之前的 $1$ 个球给甲。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人共有 $11$ 个球，拿出 $1$ 个球，将剩下的球平均分给两人，再把之前的 $1$ 个球给甲。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙多 $\_\_\_\_$ 个球。

甲乙二人共有 $10$ 个球，拿出 $2$ 个球，将剩下的球平均分给两人，每人有 $\_\_\_\_$ 个球。

甲乙二人共有 $10$ 个球，拿出 $2$ 个球，将剩下的球平均分给两人，再把之前的 $2$ 个球给甲。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙多 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，拿出 $10$ 个球，将剩下的球平均分给两人，每人有 $\_\_\_\_$ 个球。再把之前的 $10$ 个球给甲。甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球，甲比乙多 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $10$ 个球，则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $20$ 个球，则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人共有 $100$ 个球，甲比乙多 $30$ 个球，则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人球一样多，甲给乙 $5$ 个球后，甲比乙少 $\_\_\_\_$ 个球。

甲乙二人球一样多，为了让甲比乙多 $20$ 个球，乙需要给甲 $\_\_\_\_$ 个球。

和倍问题（一）

甲有 $1$ 个球，乙有 $4$ 个球。乙的球数是甲的 $\_\_\_\_$ 倍。

甲有 $1$ 个球，乙有 $4$ 个球。二人共有 $\_\_\_\_$ 个球，总球数是甲的 $\_\_\_\_$ 倍。

甲乙二人一共有 $5$ 个球，乙的球数是甲的 $4$ 倍。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $5$ 个球，甲的球数是乙的 $4$ 倍。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲有 $20$ 个球，乙有 $40$ 个球。乙的球数是甲的 $\_\_\_\_$ 倍。

甲有 $20$ 个球，乙有 $40$ 个球。二人共有 $\_\_\_\_$ 个球，总球数是甲的 $\_\_\_\_$ 倍。

甲乙二人一共有 $60$ 个球，乙的球数是甲的 $2$ 倍。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $60$ 个球，乙的球数是甲的 $3$ 倍。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $60$ 个球，乙的球数是甲的 $4$ 倍。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $60$ 个球，乙的球数是甲的 $5$ 倍。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

和倍问题（二）

甲有 $1$ 个球，乙有 $2$ 个球。甲乙二人一共有 $\_\_\_\_$ 个球，甲的球数是乙的 $\dfrac{1}{2}$ 。

甲乙二人一共有 $3$ 个球，甲的球数是乙的 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲有 $2$ 个球，乙有 $4$ 个球。甲乙二人一共有 $\_\_\_\_$ 个球，甲的球数是乙的 $\_\_\_\_$ 。

甲乙二人一共有 $6$ 个球，甲的球数是乙的 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $12$ 个球，甲的球数是乙的 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $60$ 个球，甲的球数是乙的 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲有 $1$ 个球，乙有 $3$ 个球。甲乙二人一共有 $\_\_\_\_$ 个球，甲的球数是乙的 $\_\_\_\_$ 。

甲乙二人一共有 $4$ 个球，甲的球数是乙的 $\dfrac{1}{3}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲有 $2$ 个球，乙有 $6$ 个球。甲乙二人一共有 $\_\_\_\_$ 个球，甲的球数是乙的 $\_\_\_\_$ 。

甲乙二人一共有 $8$ 个球，甲的球数是乙的 $\dfrac{1}{3}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $12$ 个球，甲的球数是乙的 $\dfrac{1}{3}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙二人一共有 $60$ 个球，甲的球数是乙的 $\dfrac{1}{3}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

分数倍数（一）

甲有 $2$ 个球，乙有 $3$ 个球。乙比甲的球数多一半。甲乙共有$\_\_\_\_$ 个球。

甲有 $2$ 个球，乙有 $3$ 个球。乙比甲的球数多 $\_\_\_\_$ （分数）。甲乙共有 $\_\_\_\_$ 个球。

甲有 $4$ 个球，乙比甲的球数多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共 $\_\_\_\_$ 个球。

甲有 $6$ 个球，乙比甲的球数多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共有 $\_\_\_\_$ 个球。

甲有 $8$ 个球，乙比甲的球数多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共有 $\_\_\_\_$ 个球。

甲有 $10$ 个球，乙比甲的球数多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共有 $\_\_\_\_$ 个球。

甲乙共有 $5$ 个球，乙比甲的球数多一半。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $10$ 个球，乙比甲的球数多一半。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $15$ 个球，乙比甲的球数多一半。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $20$ 个球，乙比甲的球数多一半。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $25$ 个球，乙比甲的球数多一半。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

分数倍数（二）

甲有 $2$ 个球，乙有 $5$ 个球。乙是甲的球数两倍还多一半。甲乙共有$\_\_\_\_$ 个球。

甲有 $2$ 个球，乙有 $5$ 个球。乙是甲的球数两倍还多 $\dfrac{1}{2}$ 。甲乙共有 $\_\_\_\_$ 个球。

甲有 $4$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共 $\_\_\_\_$ 个球。

甲有 $6$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共有 $\_\_\_\_$ 个球。

甲有 $8$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共有 $\_\_\_\_$ 个球。

甲有 $10$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则乙有 $\_\_\_\_$ 个球，甲乙共有 $\_\_\_\_$ 个球。

甲乙共有 $7$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $14$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $21$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $28$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

甲乙共有 $35$ 个球，乙是甲的球数 $2$ 倍还多 $\dfrac{1}{2}$ 。则甲有 $\_\_\_\_$ 个球，乙有 $\_\_\_\_$ 个球。

(Chen 2014) - page 16 “Problem 12”↩︎
(Chen 2016)- page 54 “Example 4” ↩︎
(Chen 2016)- page 54 “Example 4”↩︎
(Chen 2016) - page 62 “Example 19”↩︎
摘录自 (Chen 2016) - page 63 “Example 20”↩︎
摘录自 (Chen 2016) - page 64 “Example 21”↩︎
摘录自 (Chen 2016) - page 64 “Example 22”↩︎
摘录自 (Chen 2016)-page81 “Example 6”↩︎
摘录自 (Chen 2016)-page94 “Example 23”↩︎
摘录自 (Chen 2016)-page82 “Example 7”↩︎
摘录自 (Chen 2016)-page84 “Example 9”↩︎
摘录自 (Chen 2016)-page84 “Example 10”↩︎
摘录自 -page92 “Example 20”↩︎
摘录自 (Chen 2016)-page110 “Example 1”↩︎
摘录自 (Chen 2016) - page 112 “Example 3”↩︎
(孙文先 2017b)-page 340 “台湾地区选拔赛 2015 初赛二试题目 2”↩︎
摘录自 (Chen 2016)-page53 “Example 3”↩︎
摘录自 (Chen 2016)-page54 “Example 5”↩︎
摘录自 (Chen 2016)-page55 “Example 6”↩︎
摘录自 (Chen 2016)-page79 “Example 3”↩︎
摘录自 (Chen 2016) - page78 “Example 2”↩︎
摘录自 (Chen 2016)-page80 “Example 4”↩︎
摘录自 (Chen 2016)-page81 “Example 6”↩︎
摘录自 (Chen 2016)-page111 “Example 2”↩︎
摘录自 (Chen 2016) - page 112 “Example 4”↩︎
摘录自 (Chen 2016) - page 68 “Problem 24”↩︎
(孙文先 2017b)-page 254 “台湾选拔赛2013复赛一试第 1 题”↩︎
改编自(孙文先 2017b)-page 298 “台湾选拔赛2014复赛一试第 3 题”↩︎
摘录自 (Chen 2016) - page 68 “Problem 22”↩︎
(孙文先 2017a)-page 372 “台湾选拔赛2007复赛一试第 11 题”↩︎
(孙文先 2017a)-page 137 “台湾选拔赛2003初赛二试第 4 题”↩︎
(孙文先 2017a)-page 193 “台湾选拔赛2004复赛一试第 4 题”↩︎
(孙文先 2017b)-page 254 “台湾选拔赛2013复赛一试第 3 题”↩︎
(孙文先 2017b)-page 298 “台湾选拔赛2014复赛一试第 3 题”↩︎

数量关系（一）

和差问题

和差问题的几何作图

和差问题的算术解法

和差问题的方程解法（四年级选学）

代数描述和求解公式（四年级选学）

几何观点

代数观点

稍微复杂的和差问题

间接地给出和差条件

涉及三个量的和差关系

涉及物理、几何或其它常识

和倍问题

和倍问题的几何作图

和倍问题的数量计算

稍微复杂的和倍问题

差倍问题

差倍问题的几何作图

差倍问题的数量计算

分数表示的倍数关系

和差问题（一）

和差问题（二）

和倍问题（一）

和倍问题（二）

分数倍数（一）

分数倍数（二）

参考文献