进位制和记数法
1 中国劳动人民,在长期的实践中,创造与发展了记数、分数、小数、正负数以及无限逼近任一实数的办法,实质上达到了整个实数系统的完成。特别是自古就有了完美的 10 进位位值制的记数法。这是中国的独特创造,是世界其他古代民族都没有的。这一创造对世界文化贡献之大,如果不能与火的发明相比,也是可以与火药、指南针、印刷术一类发明相媲美的。
十进制记数和阿拉伯数字
中国在商代就已经采用十进制记数法,是最早采用十进制记数的文明。印度人在此基础上发明了“零”和今天普遍采用的数字记号。这是两个东方古国对世界文明重要的贡献。今天我们普遍采用 0 1 2 3 4 5 6 7 8 9 这十个数字进行记数,数字在个位、十位、百位或千位则表示不同的位值。值得一提的是,在人类文明的早期,十进制并不是理所当然的。古巴比伦人虽然有位值的概念,但采用了六十进制。古希腊和古罗马人采用了五进制和累加法表示数字。古埃及人用有限的几个象形符号来表示不同的数字,在表示较多数量时采用累加法。

图 2 给出了除中国之外,世界各主要文明在发展过程中形成的记数符号。最后一行就是我们今天使用的“阿拉伯数字”,这是先由印度人发明,再经阿拉伯人传播到欧洲的数字符号。这种符号成为今天世界各地统一使用的符号,是不同语言文化民族之间的联系纽带。

十进制记数系统的要点
- 所有的数字都是由 \(10\) 个符号构成 \((0,1,2,3,4,5,6,7,8,9)\) ;
- 符号所处位置代表的值基于 \(10\) 的不同方幂。
示例: 将十进制数 \(5643\) 表示成 数字乘以 \(10\) 的方幂的形式。
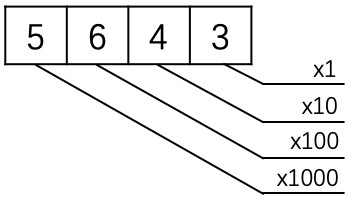
\[5643=5\times10^3+6\times10^2+4\times10^1+3\times10^0\]
图 3 标记了十进制记数法的位值。☐
十进制记数法有一些特殊的结论,可以用于计算或验算,也是小学数学考试中喜闻乐见的题目类型。由于并非本章讨论的重点,所以只列出一个性质供读者参考:
十进制数除以 \(9\) 的余数
十进制数如果能被 \(9\) 整除,那么它的各位数字之和也能被 \(9\) 整除。更进一步地说,一个十进制数除以 \(9\) 的余数等于其各位数字之和除以 \(9\) 的余数。
示例: 计算 \(121\) 除以 \(9\) 的余数。
解 直接计算余数只需要将 \(121\) 的各位数字相加:\(1+2+1=4\) ,就可以得到余数 \(4\) 。数学家用以下记号表示两个数除以 9 的余数相同:\[121\equiv1+2+1\equiv4 \mod 9\]
☐
示例: 计算 \(123456789\) 除以 \(9\) 的余数。
解 将各位数字相加: \[1+2+3+4+5+6+7+8+9\equiv45\] \(45\) 是 \(9\) 的倍数,所以 \(123456789\) 能够被 \(9\) 整除,余数为 \(0\) 。☐
思考与讨论
- 上述性质为什么是正确的?
- 构造一个证明,对任意长度的十进制数证明该性质。
根据以上推理过程,再思考思考:
思考与讨论
- 如何判断十进制数被 3 除的余数特性?
- 如何判断十进制数被 2 4 8 16 除的余数特性?
- 如何判断十进制数被 5 25 125 除的余数特性?
- 如何判断十进制数被 11 除的余数特性?
外星球的八进制
我们这个星球的人们最终选择了十进制作为日常生活中的记数手段。如果另外星球的智慧生物有八根手指,那么他们很有可能会选用八进制作为他们的基础进位制,即“逢八进一”。他们可能会如图 4 所示记数。

当然更加靠谱的方法是也采用和我们星球类似的阿拉伯数字系统。如果也采用我们的数字符号,他们只需要 0-7 这八个数字。如图 5 所示。

这个星球的小学生也学习加法。他们的加法表和乘法表如表 6 所示。请你将其中尚未计算完成的部分补充完整。
--------------------------`加法表`--------------------------
1+1= 2
1+2= 3 2+2= 4
1+3= 4 2+3= 5 3+3= 6
1+4= 5 2+4= 6 3+4= 7 4+4=10
1+5= 6 2+5= 7 3+5=10 4+5=11 5+5=12
1+6= 7 2+6=10 3+6=11 4+6=12 5+6=13 6+6=14
1+7=10 2+7=11 3+7=12 4+7=13 5+7=14 6+7=15 7+7=16
--------------------------`乘法表`--------------------------
1x1=1
1x2=2 2x2= 4
1x3=3 2x3= 6 3x3=
1x4=4 2x4=10 3x4= 4x4=
1x5=5 2x5=12 3x5=17 4x5=24 5x5=
1x6=6 2x6=14 3x6=22 4x6=30 5x6= 6x6=
1x7=7 2x7=16 3x7=25 4x7= 5x7= 6x7= 7x7=61
学习其它进位制的意义
- 信息时代用来表示数据和存储数据往往使用其它进位制,如二进制、八进制和十六进制;
- 学习其它进位制能够更好地理解数字和计算;
- 各种进位制的计算和转换是算术的绝佳练习;
示例: 计算八进制加法 \(34+56\)
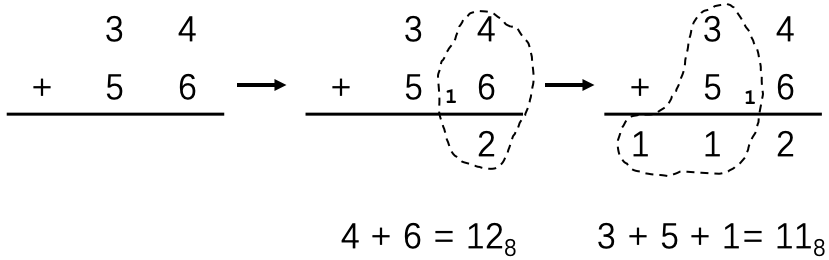
☐
示例: 计算八进制的乘法 \(34\times56\)

☐
思考与讨论
- 在八进制中,有没有类似十进制的除以 9 余数的快速判别规律?
- 在八进制中,有没有类似十进制的除以 2 和 5 余数的快速判别规律?
示例: 计算八进制的加法 \(56+78\)
示例: 计算八进制的乘法 \(56\times78\)
进位制转换
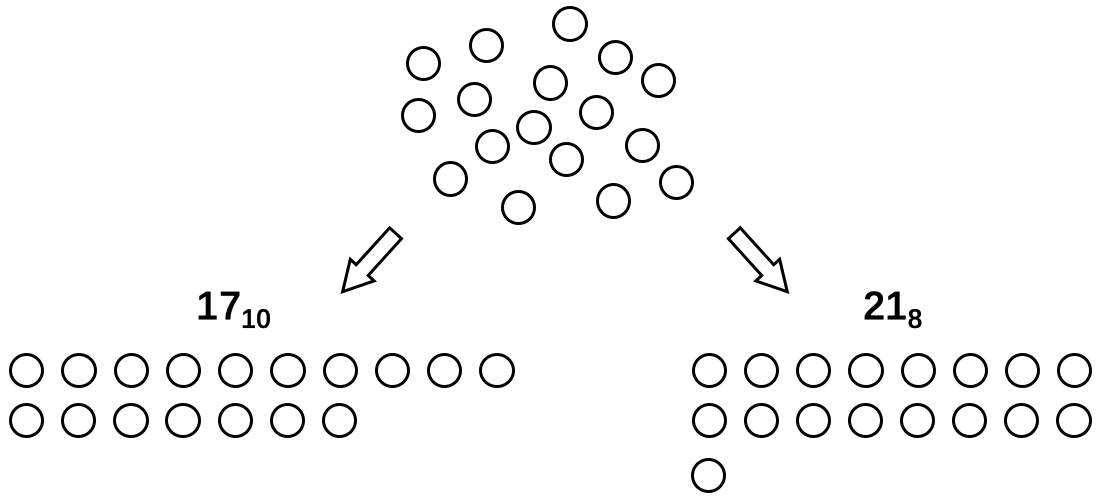
同样多的数量可以用不同的进位制记数,如图 9 所示。如何在进位制之间进行转换呢?因为我们习惯于十进制,所以首先学习利用以十进制为基础的计算方法。在下文中,我们首先讨论从其它进位制向十进制的转换,再讨论从十进制向其它进位制的转换。最终我们将抛弃十进制的特殊地位,讨论各种进位制的转换问题。
从八进制转换为十进制
用石头子记数的方法,可以很容易理解进位制的转换。
用石头子完成从八进制向十进制的转换
- [1.] 按照“一兑八”的换算方式将数字换成一堆石头子;
- [2.] 按照“逢十进一”的规则将石头子数成十进制。

以八进制数 \(21_8\) 为例,这个转换的过程如图 10 所示。如果以十进制记数法进行计算,那么就无需特别地去做“逢十进一”操作,计算过程如下所示: \[21_8=2_{10}\times8_{10}+1_{10}=17_{10}\]
示例: 将八进制数 \(1234_8\) 转换为十进制数。
根据不同位置数字的含义,可以列出以下算式: \[1\times8^3+2\times8^2+3\times8+4=668_{10}\]☐
Windows/Mac/Linux 等操作系统自带的计算器可以完成八进制到十进制的转换。在练习中,你可以使用这种手段进行验算。
使用左侧 ID 号访问演示视频。
从十进制转换为八进制
使用除法来转换十进制数字为其它进位制。例如十进制数字 \(17_{10}\) , \(8\) 个 \(1\) 组,能分出 \(2\) 组还余 \(1\) 个。也就是 \(17_{10}=21_8\) 。

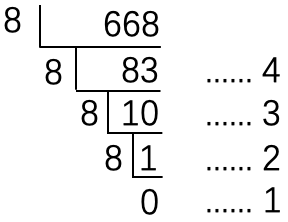
示例: 将十进制数 \(668_{10}\) 转换为八进制数。
解法一 从高位至低位,将 \(668\) 拆解成 \(8\) 的幂次之和。
- 首先是 \(8^3=512\) ,\(668\) 去掉 \(512\) 还剩 \(156\) ;
- 然后是 \(8^2=64\) , \(156\) 可以去掉 \(2\) 个 \(64\) 剩下 \(28\) ;
- 然后是 \(8\) , \(28\) 去掉 \(3\) 个 \(8\) 剩下 \(4\) 。
☐
☐
思考与讨论
- 如何使用十进制完成五进制和八进制之间的转换?
- 如何不使用十进制完成五进制和八进制之间的转换?
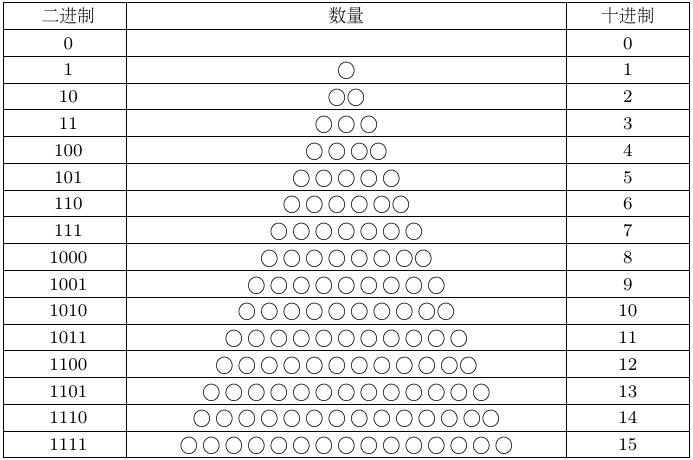
二进制
二进制在信息时代发挥着至关重要的作用。二进制只有两个符号, \(0\) 和 \(1\) 。现代的二进制是法国数学家莱布尼茨发明的,相传他受到了中国八卦图的启发。
二进制与十进制的转换
使用类似的 节的方法,可以很容易地进行二进制记数和十进制记数的转换。
示例: 将二进制数 \(110101_2\) 转换为十进制记数。 \[110101_2 = 1\times2^5+1\times2^2+1\times2^2+1=32+16++4+1=53_{10}\]☐
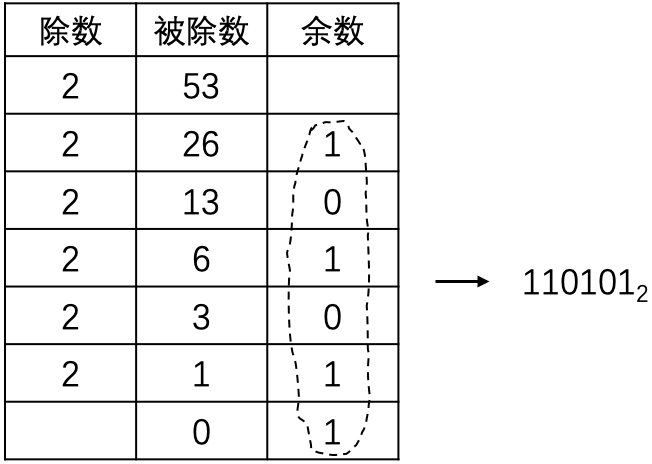
示例: 将十进制数 \(53_{10}\) 转换为二进制记数。 \[53=32+16+3+1=110101_2\]
也可以使用连续的带余除法完成转换,如图 14 所示,可以得到相同的结果。☐
用二进制计算
二进制的基本计算规则很简单:
- 加法:\(0+0=0\), \(0+1=1\), \(1+0=1\), \(1+1=10\)
- 减法:\(0-0=0\), \(1-0=1\), \(1-1=0\), \(10-1=1\)
- 乘法:\(0\times0=0\), \(0\times1=0\), \(1\times0=0\), \(1\times1=1\)
- 除法:\(0\div1=0\), \(1\div1=1\)
计算 \(1101_2\times1011_2\) 。

☐
古代记数法
正字记数法 (Tally Numeration System)
人类最初的计数是使用石头、木棍或者刻道。摘了多少苹果,就在洞穴的石壁上划多少道。划道多了不好清点,就五个一组,如图 16 所示。

这种记数法在今天也很常见,我们选举班干部时,就经常使用“画正字”的方法统计选票。
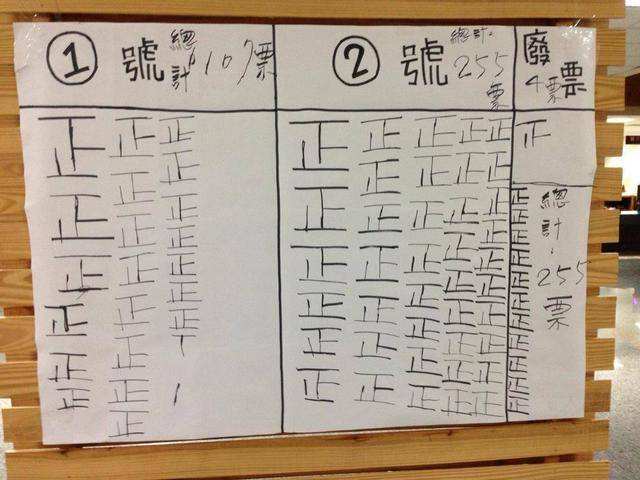
这种记数方法的好处是无需改变已有的记号就可以不断地递增记数。想象一下,如果你是原始人,在洞穴上刻阿拉伯数字,不断地跟随增加的苹果数简直是一场灾难。
古埃及记数法
古埃及文明在公元前 3400 年发展出自己的记数法。古埃及人用单独的符号表示整十整百,如图 18 所示,但依然用划道表示 1 到 9 。较复杂的多位数则通过重复这些符号来表示。
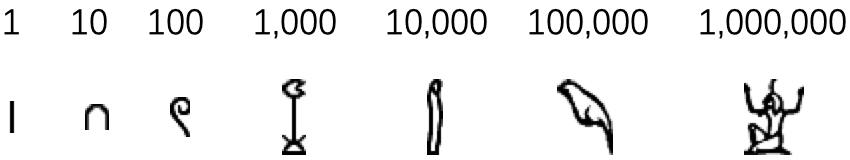

举例来说,埃及卡纳克神庙中的一个石刻如图 20 所示,它表示 \(4622\) 这一数字。可以发现,古埃及人并没有发明类似 \(1-9\) 的数字,相反他们把不同的记号用于表示不同的位值。这种计数方法使用起来其实很繁琐。

扩展学习:古埃及人创造了灿烂的文明,观看左侧 ID 所示视频,了解古埃及人的数学。
思考与讨论
- 汉语也有“个十百千万”这些符号,这被称为“万字记数”,和古埃及的符号有何异曲同工之处?
- 汉语是如何表示大数字的,对比古埃及人有何优势?
古巴比伦记数法
古巴比伦人采用六十进制。 \(1-59\) 的 \(59\) 个数字由两个符号构成。\(\blacktriangledown\) 代表 \(1\) ,\(<\) 代表 \(10\) 。

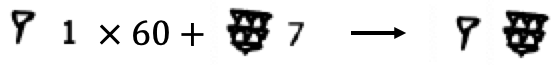
图 21 是古巴比伦人的记数法。古巴比伦人对于 \(60\) 以上的数,采用位置计数。例如:\(67_{10}=1\times60+7\) ,巴比伦人会先用表示 \(1\) 的符号在高位标记,然后用表示 \(7\) 的符号在低位标记,如图 所示。
示例: 将 \(524551_{10}\) 转化为巴比伦记数符号。
解: 首先先用连续除法将其转换为 60 进制记数:

再将其制作成巴比伦符号:
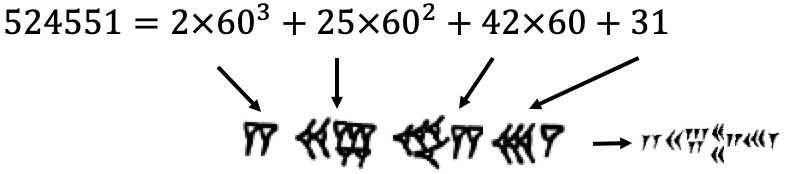
☐
古代巴比伦的数学成就
古巴比伦人取得了灿烂的数学成就,图 25 所示的 Plimpton 322 号石碑是目前发现的最古老的三角函数表。对这块有着 3700 年历史的石碑的研究表明,古巴比伦人对三角形(尤其是直角三角形)的研究比希腊人早了 1000 多年,那时中国还处在传说的夏朝。这些古老的数学知识一直被隐藏着,直到最近才被发现。
观看左侧 ID 所示视频,了解古巴比伦人的数学。

思考与讨论
- 比对一下古巴比伦人和古埃及人的记数法;
- 古巴比伦人的六十进制对今天有什么影响?
- 古代中国的“万字记数”,比古巴比伦人的记数法有何优势?
古玛雅记数法
玛雅文明使用的二十进制记数系统。玛雅数字的 1 到 19 使用点和横线表示。点表示 1 ,横线表示 5 。玛雅文明使用贝壳代表 0 ,这在记数系统中非常关键。在我们之前讲的古埃及文明和古巴比伦文明是没有符号 0 的,在涉及某些数字时会非常不便。

将 \(2005_{10}\) 转化为玛雅记数符号。
使用连续除法将其转换为 20 进制记数: \[2005=5\times20^2+0\times20+5\]
再将其转换为玛雅记数符号:
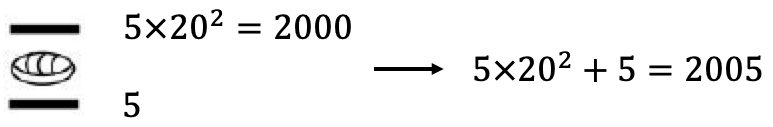
☐
罗马记数法
罗马记数法从公元前 3 世纪就开始欧洲使用,直到今天依然应用广泛,如图 28 所示是一些常见的罗马数字的应用场景。

罗马数字的基本形式是把这些字母代表的数字加起来。例如 MDCLXVI 代表 \(1000+500+100+50+10+1=1666\) , CCCXXVIII 代表 \(100+100+200+10+10+5+1+1+1=328\) 。
为了避免连续四个同样的字符的冗赘,在中世纪时罗马人引入了减性符号,如果一个比较小的符号在大符号左侧,那么代表的数字是二者相减。比如 IV 代表 \(5-1=4\) , XC 则代表 \(100-10=90\) 。
示例: 罗马数字 XCI 和 LXXIX 对应的阿拉伯数字是什么?
XC 代表 \(90\) , I 代表 \(1\) 。综上, XCI 代表 \(91\) 。
LXXX 代表 \(80\) , IX 代表 \(9\) 。 综上, LXXIX 代表 \(89\) 。
☐
为了表示大数字,罗马人用上划线表示乘以 1000 。例如 \(\rm \overline{V}\) 表示 \(5\times1000=5000\) , \(\rm \overline{\overline{V}}\) 则表示 \(5\times1000\times1000=5,000,000\) 。
示例: 罗马数字 \(\rm \overline{\overline{\overline{CXI}}}\) 和 \(\rm \overline{D}CLIX\) 对应的阿拉伯数字是什么?
\(\rm \overline{\overline{\overline{CXI}}}\) 表示 \(111\times1000^3=111,000,000,000\)
\(\rm \overline{D}CLIX=\overbrace{(500\times1000)}^{\overline{D}}+\overbrace{(100+50)}^{CL}+\overbrace{(10-1)}^{IX}=500,159\)
☐
思考与讨论
- 找找你身边的罗马数字,你能认出来么?
练习: 将 \(3282_{10}\) 写成展开式。
练习: 计算下列八进制算式:
- \(67_8+45_8\) b. \(67_8\times45_8\)
练习: 八进制和十进制的互相转换:
- [a.] 将八进制数 \(3720_8\) 转换为十进制数
- [b.] 将十进制数 \(1234_{10}\) 转换为八进制数
练习: 计算下列二进制算式:
- [a.] \(1011_2+1101_2\)
- [b.] \(1011_2\times1101_2\)
练习: 二进制和十进制的互相转换:
- [a.] 将二进制数 \(101011_2\) 转换为十进制数
- [b.] 将十进制数 \(198_{10}\) 转换为二进制数
练习: 利用古埃及记数法解决以下问题:
- [a.] 使用古埃及记数法表示 1,312,322 。
- [b.] 考古学家在金字塔里发现了这样一幅壁画,如图 30 所示。你能破译出这幅壁画的数字么?