逻辑与推理

“亚里士多德的影响在许多不同的领域里都非常之大，但以在逻辑学方面为最大。 …… 文艺复兴以后，这种至高无上的地位大部分是丧失了，但在逻辑学上他仍然保持着至高无上的地位。甚至于直到今天 ……”¹

命题

示例：² 以下句子不是命题，因为无法判断真伪。

• [1.] 她有蓝色的眼睛；
• [2.] 一个数加上 \(7\) 等于 \(18\)；
• [3.] \(2 + 3\) ；
• [4.] 《小猪佩奇》是最好看的动画片；

☐

命题的否定

如果某个命题是真的，那么它的否定就是假的，反之如果该命题是假的，那么它的否定就是真的。总之，命题和自身的否定，真假各居其一。例如，命题“正在下雪”的否定是“没在下雪”。

示例：³ 写出以下命题的否定：

• [a.] \(2+3=5\) ；
• [b.] 菱形恰好有 \(4\) 条边；
• [c.] 五边形恰好有 \(4\) 条边；

答上述命题否定如下：

• [a.] \(2+3\neq5\) ；
• [b.] 菱形不是 \(4\) 条边；
• [c.] 五边形不是 \(4\) 条边；

  ☐

  
  

示例： 写出以下命题的否定：

• [a.] 今天班里有些同学没交作业；
• [b.] 今天班里有些同学交作业了；
• [c.] 等差数列加等差数列，结果都是等差数列；
• [e.] 所有的等差数列的各项都不相等；

答

• [a.] 今天班里所有的同学都交作业了；
• [b.] 今天班里没有同学交作业；
• [c1.] 等差数列加等差数列，结果不一定是等差数列；
• [c2.] 至少有一对等差数列相加的结果不是等差数列；
• [e.] 至少存在一个等差数列，它至少有两项是相等的；

  ☐

  
  

掌握如何否定一个命题在数学学习中是非常重要的。例如某题目要求讨论是否“全部的自然数都具有某种性质”，如果认为正确就需要严格的证明，如果认为错误则只需要找到一个反例即可。因为“全部的自然数都具有某种性质”的否定形式是“至少存在一个自然数不具有该性质”。

示例：⁴ General forms of quantified statements with their negations follow.

statements with their negations

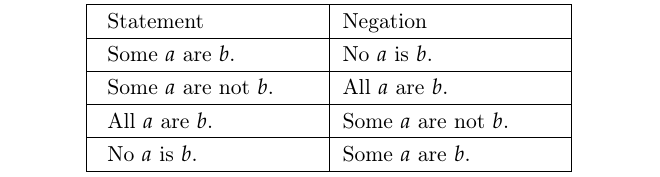
示例：⁵ Negate each of the following regardless of its truth value:

• [a.] All students like hamburgers.
• [b.] Some people like mathematics.
• [c.] There exists a natural number \(n\) such that \(3n=6\).
• [d.] For all natural numbers \(n\), \(3n=3n\).

Solution

• [a.] Some students do not like hamburgers.
• [b.] No people like mathematics.
• [c.] For all natural numbers \(n\), \(3n\neq6\).
• [d.] There exists a natural numbers \(n\) such that \(3n\neq3n\).

  ☐

  
  

逆命题、否命题和逆否命题

逆命题 (converse statements) 、否命题 (inverse) 和逆否命题 (contrapositive) 定义很拗口，先给出这几种命题的示例，再来看定义。

示例： 以下四个命题，原命题是真命题。逆命题、否命题和逆否命题的真假性如何？

猫科动物的命题

猫科动物 不明来源图片

☐

你看过上面的这些命题之后，能不能给出逆命题、否命题和逆否命题的定义呢？在学习新概念时，通过一些简单实例入手找到规律，再看那些枯燥的定义就会觉得容易很多了。下面给出了这几种命题的定义：

示例： 写出命题“如果某人在北京，那么他一定在中国。”的逆命题、否命题和逆否命题。

答 根据定义，所要求之命题如下：

• 逆命题：如果某人在中国，那么他一定在北京；
• 否命题：如果某人不在北京，那么他一定不在中国；
• 逆否命题：如果某人不在中国，那么他一定不在北京；

  ☐

  
  

演绎推理和三段论

三段论

示例： 下面展示了一个典型的三段论结构。图 4 所示的欧拉图 (Euler Diagram) 也表示了该关系。

欧拉图

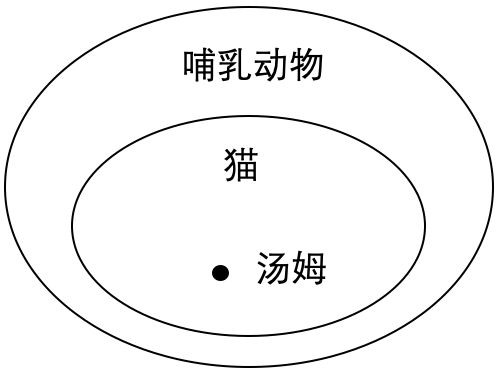
• [] 所有的猫都是哺乳动物。（大前提）
• [] 汤姆是一只猫。（小前提）
• [] 汤姆是哺乳动物。（结论）

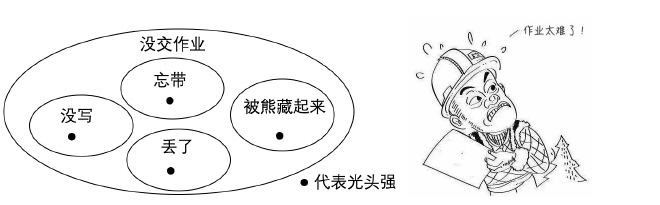
示例： 以下论述结构是正确的么？

• [] 所有没写作业的同学都没交作业。
• [] 光头强没交作业。
• [] 所以光头强没写作业。

☐

在数学论证和推理过程中，我们无时无刻不在使用这种三段论结构，只是有的时候我们并没有明确地说出大前提、小前提和结论。例如我们对数列 \(1, 2, 3, 4, 5, ... , 99, 100\) 求和。完整的三段论推理如下：

• [] 所有的等差数列的和都是首项加末项乘以项数除以 \(2\) 。（大前提）
• [] \(1, 2, 3, 4, 5, ... , 99, 100\) 是等差数列。（小前提）
• [] 所以该数列的和是\((1+100)\times100\div2=5050\)。（结论）

使用逆否命题进行推理

示例： 下面的三段论是一个使用逆否命题进行推理的示例：

• [] 如果某个图形是正方形，那它也是矩形。
• [] 这个图形不是矩形。
• [] 所以这个图形不是正方形。

示例： 使用逆否命题结构，从以下条件推导结论：

• [] 大前提：如果某人住在海淀区，那么他/她一定住在北京
• [] 小前提：王老师不住在北京。

解： 大前提的逆否命题是：

如果某人不住在北京，那么他/她一定不住在海淀区。

既然大前提正确，逆否命题也是正确的。注意到小前提恰好是这个逆否命题中的条件部分。于是我们推导出结论为：

☐

示例：⁶ 如图 6 所示的每张牌的正面有圆形或星形图案，背面则有三角形或正方形图案。为了验证“有星形图案的卡牌一定也有三角形图案”这一命题，你需要掀开哪几张牌？

印有图案的卡牌

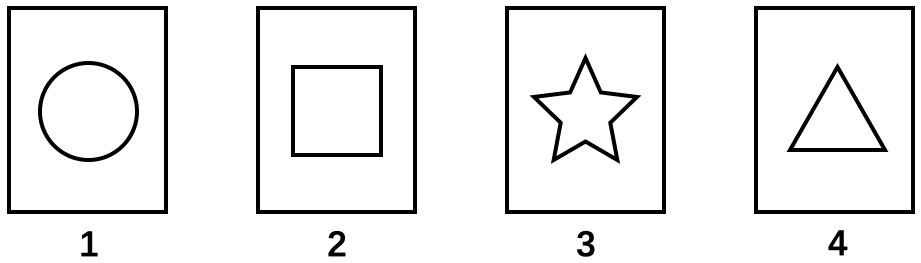
解 我们需要首先验证：“如果某张牌的正面是星形，那么背面一定是三角形”。为达这一目的，需要掀开正面有五角星标记的卡牌，以验证其背面是否是三角形。在本例中需要掀开 \(3\) 号牌。

接下来我们需要验证逆否命题“如果某张牌的背面不是三角形，那么正面一定不是星形”。为达这一目的，需要掀开背面不是三角形标记的卡牌，已验证其正面不是星形。在本例中需要掀开 \(2\) 号牌。（请注意， \(1\) 号牌无需掀开，因为圆形是正面标记。）

☐

使用逻辑链条推理

将 “如果 … ，那么 …” 句式连接起来，也是常见的推理手段。例如：

• [] 条件 \(1\) ：如果我放学后抓紧写作业，就能在六点之前写完。
• [] 条件 \(2\) ：如果我在六点之前写完作业，晚上就能看动画片。
• [] 结论：如果我放学后抓紧写作业，晚上就能看动画片。

你能够举出一个逻辑链条推理的例子么？

推理技巧

在实际问题中，往往要综合使用各种推理技巧。此处的列出的推理技巧也远远无法涵盖各种问题。本节将通过一组示例，向你展示这些在推理过程中的常见技巧。要想提高自己的逻辑推理能力，最好的办法是尝试各种类型的推理题目。

示例：⁷ 排序推理：淘气、笑笑、奇思、妙想和智慧老人排成一排。淘气在奇思的后面，但是在妙想的前面。智慧老人在笑笑的前面，但是在奇思的后面。妙想在笑笑的前面。请问谁排在第一位？

解： 我们用字母代替人名，重新标注一遍题目。

在题目上标注

根据条件一，我们就排三个人：

CAD

然后我们看看条件二和条件三哪个更容易处理。显然是后者。根据条件三，我们把 B 放在 D 的后面。

CADB

☐

示例：⁸ 三位外籍教师在聚餐，分别是数学老师怀特 (White) 、科学老师布莱克 (Black) 和历史老师里德 (Red) 。其中一位黑头发的老师兴奋地说：“真巧，咱们三个人正好分别是白头发、黑头发和红头发，而且没人的名字和头发颜色一样”。“是啊”，怀特老师答道。请问历史老师的头发是什么颜色的？

☐

解法二 使用连线图能够将上述推理过程形象化地表现出来。

步骤一：“没人的名字和头发颜色一样”，根据该条件画出图 8 左图，其中虚线表示排除的关系。

步骤二：“怀特老师回答黑头发老师的话”，根据该条件排除怀特老师是黑色头发的可能性，补充虚线如图 8 右图：

排除关系

步骤三：于是可以直观地看出，怀特老师只能是红色头发，如图 9 左图添加实线：

步骤四：于是布莱克老师和里德老师的头发颜色就一目了然了，补充最后的实线关系如图 9 右图所示：

确定关系

☐

示例：⁹ 有红黄蓝三个不同颜色的盒子。有一个盒子里有苹果。以下命题，有且只有一个是真的：

• 苹果在红色的盒子里；
• 苹果不在黄色的盒子里；
• 苹果不在红色的盒子里；

问苹果在哪个盒子里？

☐

示例：¹⁰ 逻辑关系：邓布利多有三块魔法石，颜色分别是白红蓝，镶嵌成一个三角形（上、左下、右下）。以下三个命题有且只有一个是真的：

魔法三角形 （取自日本漫画）

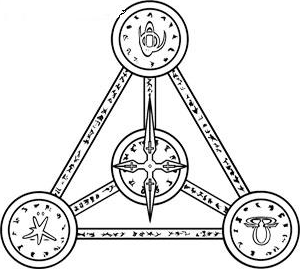
• 上面的魔法石是红色的；
• 左下的魔法石不是蓝色的；
• 右下的魔法石不是红色的；

问左下方的魔法石是什么颜色的？

示例：¹¹ 分组称重：一位珠宝商有四根金条。他知道其中有一根是假的，重量和另外三根不太一样。为了找出这根假金条，他需要至少用天平称几次？

¹² 麦格教授拿出了三顶魔法帽，两顶白色的，一顶黑色的。她把赫敏和哈利的眼睛蒙上，然后给每人带了一顶帽子后把眼罩取下，让他们猜自己头顶上的帽子颜色。赫敏和哈利都只能看到对方头上的帽子颜色而看不到自己的。两个人对视了一会儿，赫敏忽然大喊，“我知道我头上的帽子颜色了！”请问她是如何判断的？

练习：¹³ 指出下列哪些句子是命题，并判断其真假。

• [a.] \(2+4=8\) ；
• [b.] 北京是中国的首都；
• [c.] 现在几点了？
• [d.] \(3\cdot2=6\) ；
• [e.] 这是一个假命题； \(\bigstar\)

练习： 写出命题“正方形是矩形”的逆命题、否命题和逆否命题，并指出各个命题的真假。

练习：¹⁴ 麦格教授拿出了五顶魔法帽，三顶白色的，两顶黑色的。这种魔法帽子让人看不到自己头上的帽子，但能够看到其他人头上的。她把罗恩、哈利和赫敏的眼睛蒙上，然后给每人带了一顶帽子。

麦格教授首先把罗恩的眼罩摘下，罗恩看了看哈利和赫敏说道：“亲爱的麦格教授，我不知道自己头上的帽子颜色。”

然后麦格教授把哈利的眼罩摘下，哈利看了看罗恩和赫敏说到：“我也不知道自己头上的帽子颜色。”

这时候赫敏喊道：“我知道自己帽子的颜色了！”，她是如何知道的呢？

练习：¹⁵ 六个外观一样的硬币，其中有一个略微重一点。为了找到该硬币，要使用天平最少称几次？

练习：¹⁶ 在一场赛马比赛中，获得前 4 名的选手分别是神秘骑士、战争之王、真理正义和黑色闪电。已知如下条件：

赛马和骑手（不明来源图片）

• [a.] 战争之王是第 2 名或第 4 名。
• [b.] 真理正义不是冠军。
• [c.] 第 3 名是神秘骑士或黑色闪电。
• [d.] 战争之王比神秘骑士先完成比赛。

请问获得第 4 名的是哪位选手？

问题： 写出下列命题的否定形式：

• [a.] \(6<8\)
• [b.] \(3\cdot5=15\)
• [c.] 所有的狗都有四条腿。
• [d.] 有些长方形是正方形。
• [e.] 不是所有的长方形都是正方形。

问题：¹⁷ 将以下限定短语

• [1.] 对所有的自然数 \(n\) 都有 …
• [2.] 存在自然数 \(n\) 使得 …
• [3.] 不存在自然数 \(n\) 使得 …

与以下等式相连接，指出合成的命题的真假性。

• [a.] \(n+8=11\)
• [b.] \(n^2=4\)
• [c.] \(n+3=3+n\)
• [d.] \(5n+4n=9n\)

例如：“对所有的自然数 \(n\) 都有 \(n+8=11\)” ，这是一个假命题。

而“存在自然数 \(n\) 使得 \(n+8=11\)”，这就是一个真命题。

问题：¹⁸ 指出以下命题是真是假：

• [a.] 存在一些自然数 \(n\) 使得 \(n<6\) 并且 \(n>3\) 。
• [b.] 对所有的自然数 \(n\) 都有 \(n>0\) 或 \(n<5\) 。

问题：¹⁹ 写出以下命题的逆命题、否命题和逆否命题。

• 如果某个数 \(x=5\) ，那么 \(2x=10\) 。
• 如果你不喜欢雪，那么你就不喜欢雪上运动。
• 如果你不使用高露洁牙膏，那你就有蛀牙。
• 如果某人的逻辑推理很好，那他在本次考试中就能拿到 A 。

问题：²⁰ 写出和以下命题等价的命题：

“如果某个数是 \(8\) 的幂，那它也是 \(4\) 的幂。”

问题：²¹ 说明以下推理过程的正确性与否：

• [a.] 所有的正方形都是四边形。\ 所有的四边形都是多边形。\ 因此，所有的正方形都是多边形。
• [b.] 所有的数学家都很聪明。\ 有些数学家很富有。\ 因此，有些聪明的人很富有。
• [c.] 一年级的学生没上过科学课。\ 佩奇二年级了。\ 因此，佩奇上过科学课。

问题：²² 根据以下条件，通过正确推理作出结论：

• [a.] 有些一年级学生喜欢数学。\ 喜欢数学的人都很聪明。
• [b.] 如果丽莎认真复习，那么她就能通过律师从业资格考试。\ 如果丽莎通过律师从业资格考试，她就能拿到律师资格证。\ 如果丽莎拿到律师资格证，她就能找一份律师工作。
• [c.] 所有的等边三角形都是等腰三角形。\ 存在等边三角形。

问题：²³ 用“如果 … 那么 …”改写以下命题：

• [a.] 是正方形的图形也是矩形。
• [b.] 所有的整数都是分数。
• [c.] 恰好有三条边的多边形是三角形。

问题：²⁴ 写出下列命题的否定形式：

• [a.] \(6>8\)
• [b.] 所有的正方形都是矩形。
• [c.] 并非所有的整数都是自然数。
• [d.] 有些人长着金色的头发。
• [e.] 没有老虎长翅膀。

问题：²⁵ 将以下限定短语

• [1.] 对所有的自然数 \(n\) 都有 …
• [2.] 存在自然数 \(n\) 使得 …
• [3.] 不存在自然数 \(n\) 使得 …

与以下等式相连接，指出合成的命题的真假性。

• [a.] \(n+0=n\)
• [b.] \(n+1=n+2\)
• [c.] \(3(n+2)=12\)
• [d.] \(n^3=8\)
• [e.] \(n^2-2n+2>0\)

例如：“对所有的自然数 \(n\) 都有 \(n+0=n\)” ，这是一个假命题。

问题：²⁶ 指出以下命题是真是假：

• [a.] 存在一些自然数 \(n\) 使得 \(n>5\) 并且 \(n>2\) 。
• [b.] 对所有的自然数 \(n\) 都有 \(n>5\) 或 \(n<5\) 。

问题：²⁷ 写出以下命题的逆命题、否命题和逆否命题。

• 如果某个数 \(x=5\) ，那么 \(2x=11\) 。
• 如果某个数 \(x=3\) ，那么 \(x^2=9\) 。
• 如果下雪，取消户外活动。

问题：²⁸ 假设 “如果下雨，佩奇就去看电影。” 是真命题，那么“如果不下雨，佩奇就不去看电影。”是符合逻辑的命题么？

问题：²⁹ 说明以下推理过程的正确性与否：

• [a.] 所有的人都会死。\ 苏格拉底是人。\ 所以苏格拉底会死。
• [b.] 雨天都是阴天。\ 今天不是阴天。\ 因此，今天不是雨天。
• [c.] 很多学生喜欢滑冰。\ A 是学生。\ 因此， A 喜欢滑冰。

问题：³⁰ 根据以下条件，作出正确结论：

• [a.] 我们班的同学都喜欢吃冰激凌。\ 笑笑是我们班的同学。
• [b.] 所有的工程师都需要学习数学。\ 史密斯先生不需要学习数学。
• [c.] 所有的自行车都需要轮胎。\ 所有的轮胎都需要橡胶。

问题：³¹ 写出以下命题的否定形式：

• [a.] \(3+5\neq9\) 并且 \(3\cdot5=15\) 。
• [b.] 我去或者她去。

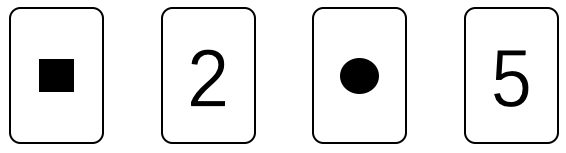
问题：³² 每张卡牌的正面是图形，背面是数字。在图 12 所示的 4 张卡牌中，你需要翻开哪几张才能够验证“每个方形的另一面都是偶数”这一命题？

双面卡牌

问题：³³ 教室的窗户被打碎了。教导主任叫了四个学生来办公室。他很确定是其中一个学生干的。

• [] Alex 说：是 Bob 干的。
• [] Bob 说：是 Dean 干的。
• [] Cam 说：不是我干的。
• [] Dean 说：Bob 说谎了。

已知有且只有一个学生说真话，问是谁打碎了玻璃？

问题：³⁴ 信封里有一张带数字的卡片。以下四个命题有 3 个是真的， 1 个是假的。

• [1.] 卡片的数字是 1 。
• [2.] 卡片的数字不是 2 。
• [3.] 卡片的数字是 3 。
• [4.] 卡片的数字不是 4 。

请问以下哪个论断一定是对的？

1. 1 是对的(B) 1 是错的(C) 2 是对的

2. 3 是对的(E) 4 是错的

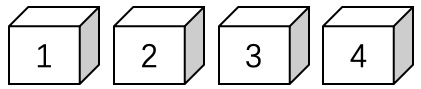
问题：³⁵ 如图 13 所示是四个带颜色的盒子。每个盒子的颜色各不相同。红色的盒子挨着蓝色的盒子。绿色的盒子挨着红色的盒子和黄色的盒子。请问红色盒子可能是几号？

带颜色的盒子

1. 只能是 1 号(B) 只能是 2 号(C) 只能是 3 号

2. 可能是 2 或 3 号(E) 可能是 1 或 4 号

问题：³⁶ 斯内普教授心里想了两个数，这两个数是 0 到 9 中连续的两个数。告诉赫敏和哈利每人一个数字，并且告知二人两个数字是连续的。然后赫敏和哈利发生了以下对话：

“哈利，我不知道你的数字。”

“赫敏，我也不知道你的。”

“哦，哈利，我知道你的数字了！”

如果哈利和赫敏的头脑都很清晰，都很有逻辑性，那么斯内普教授可能告诉了赫敏哪几个数字？

问题：³⁷ 五个人进行射箭比赛。每人射两箭。射出十箭的得分各不相同，分别是 1 到 10 环。 A 两箭共计 16 环， B 共计 4 环， C 共计 7 环， D 共计 11 环， E 共计 17 环。请问射中 6 环的那一箭是谁射中的？

\(9\) 个外观一样的小球，其中一个比其它 \(8\) 个重。用天平至少称几次，才能找出这个不一样的球？