序列与模式
“纵观历史,人类一直在试图了解物质世界的基本活动。我们尽力发现规则和模式,确定我们周围物体的特性,以及彼此之间的复杂关系。几千年来,全世界学会团体发现一个在所有学科之上的学科,产生了关于物质世界潜在真像的可靠知识。这学科就是数学。”1
模式
数学是对模式 (Patterns) 的研究,模式无处不在。人们需要辨识模式,还要清晰地描述模式。
示例: 观察如下图样2 \[\bigcirc,\triangle,\triangle,\bigcirc,\triangle,\triangle,\bigcirc,\_\_\_,\_\_\_,\_\_\_\]
- [a]. 根据模式填入空格处的图样;
- [b]. 用文字描述你找到的样式;
- [c]. 再针对如下图样,做相同的事情:
\[\bigcirc,\triangle,\bigcirc,\triangle,\triangle,\bigcirc,\triangle,\triangle,\triangle,\bigcirc,\_\_\_,\_\_\_,\_\_\_\]
示例: 有时候我们能发现一些很有趣的模式,比如以下等式:34 \[\begin{aligned} 1+0\times9&=1 \\ 2+1\times9&=11 \\ 3+12\times9&=111 \\ 4+123\times9&=1111 \end{aligned}\]
- [a]. 观察上述等式,你能找到哪些模式?
- [b]. 你能按照模式写出第 \(9\) 行算式么?
- [c]. 这些模式会继续下去么?为什么?
解: a. 我们在上述算式中至少可以观察到如下模式:
- [1]. 等号左侧的第一个加数是自然数序列;
- [2]. 等号右边的 \(1\) 的个数和最左边的自然数一样;
- [3]. 左侧第二个加数是乘积,其中第二个因子是 \(9\) 。请你描述第一个因子的模式。
在下面的方框中写入描述模式的文字。用文字清晰地描述你看到的模式。这是一种非常重要的能力

- 根据上面的观察,我们可以很容易地写出后续算式。
- 如果你断言模式不会继续,就需要找到模式在哪里终止。反之,如果你断言模式会永远继续下去,就需要证明它。
☐
在本书中用右对齐的方块表示论证或解答过程的结束
推理
上一节的示例说明,不能仅仅依靠几个情形就断定某种模式的存在。如果想确定某种模式是否存在,需要进行推理(Reasoning)。
基于观察并总结模式的手段称为归纳推理 (Inductive Reasoning) 。这种方式有时并不准确,但许多数学发现正是来源于此。可靠的证明则需要演绎推理 (Deductive Reasoning) 。
♣ 仅仅试验少数情形就得出猜想是很危险的。请看如下示例:
示例:5 如图 1 所示,在圆周上取若干点,将其两两相连。连出的线段分圆为若干部分。
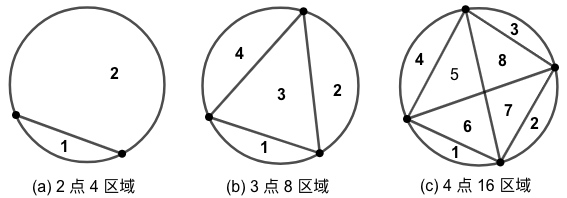
从图 1 所示的三个情形,圆分别被分为 \(4\), \(8\) 和 \(16\) 个区域,某位同学做出以下猜测:圆周上的点增加一个,区域数目增加一倍。 这个猜测对么?最简单的方法是再试上几个。在图 2 中绘制线段,计数在圆周上分别取 5 个点和 6 个点时,两两相连的弦分圆为多少部分,从而进一步验证或推翻猜想。
动手画一画
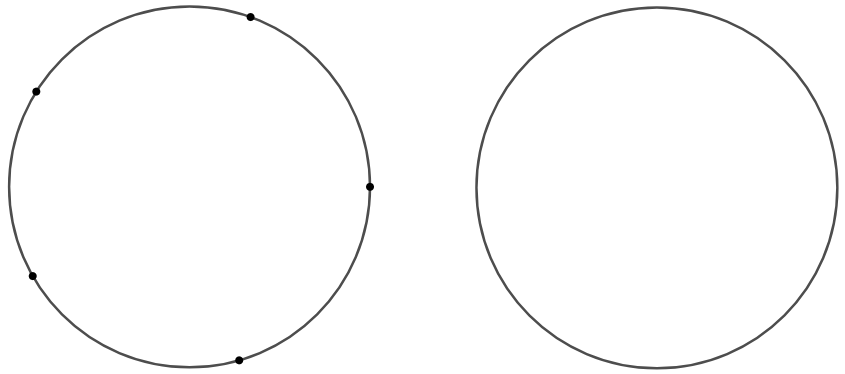 对猜想的进一步验证:a. 在圆周上取 \(5\) 个点,连线数一数;b. 在圆周上取 \(6\) 个点时请注意,六个点的位置不同,分割圆的区域也会不同。
对猜想的进一步验证:a. 在圆周上取 \(5\) 个点,连线数一数;b. 在圆周上取 \(6\) 个点时请注意,六个点的位置不同,分割圆的区域也会不同。☐
示例:6 佩奇在学习加法时发现了如下规律:
\[\begin{equation*} \begin{aligned} 4+5+6&=15=5\times 3 \\ 5+7+9&=21=7\times 3 \\ 13+16+19&=48=16\times 3 \\ 11+25+39&=75=25\times 3 \end{aligned} \end{equation*}\]
你能描述她发现的规律么?你能通过更过的例子进一步验证这一规律么?试着证明上述结论,并指出每一个步骤的依据。无论使用多少具体的例子,都无法让我们对尚未验证的无限多种可能性有十足的信心。某个结论必须经过证明才能被数学家承认。证明由一组严密的逻辑链条构成。
如果你没学过代数,也可以写出不依赖于abc 符号的证明,因为人类在没有代数工具时也能做到的。
在得到初步的结论之后(三个数求和),你能否将其扩展到更一般的结论呢?思考与讨论
质数是只能被 \(1\) 或自身整除的自然数。例如 \(2,3,5,7,11\) 都是质数。有一天,佩奇提出了一个猜想:把一个自然数自乘,加上原数,再加上 \(11\) ,将会得到一个质数。用更数学的语言来说就是如果 \(x\) 是自然数,那么 \(x^2+x+11\) 是质数。为了证明该猜想,佩奇给出了一组算式:
\[\begin{equation*} \begin{aligned} 1^2+1+11=13 \\ 2^2+2+11=17 \\ 3^2+3+11=23 \\ 4^2+4+11=31 \end{aligned} \end{equation*}\]
- [a]. 佩奇使用了归纳推理还是演绎推理?
- [b]. 再继续尝试几个数字,研究一下“佩奇猜想”;
- [c]. 你能找到该猜想的反例么,或者你能证明该猜想?
等差数列
序列 (Sequences) 是顺序排列的数字、图形或物体。数学家们喜欢研究具有某些共同属性 (Properties) 的序列。等差数列10 (Arithmetic Sequences) 是一种最常见的序列。
等差数列的定义
 以 \(3\) 开始的全部奇数构成一个等差数列。其通项公式为 \(a_n=1+2n\)
以 \(3\) 开始的全部奇数构成一个等差数列。其通项公式为 \(a_n=1+2n\)等差数列是一种数字序列。等差数列从第二项开始,每一项与前一项的差都相等。这个差称为公差。数列的第一项称为首项。如果数列项数有限,最后一项称为末项。
如果数列项数无限,可以写出前几项和省略号表示之,或给出通项公式,如图 3 所示。以下数列都是等差数列:
- \(5,7,9,11,13,15,17,19,21\)
- \(13,26,39,52,65,78,91\)
- \(17,34,51,68,85,102\)
- \(1,1,1,1,1,1\)
- \(95,76,57,38,19,0\)
思考与讨论
- 除了自然数和 \(0\) ,你还知道哪些数?
- 你能够写出由这些数组成的等差数列么?
等差数列的示例
在日常生活中,等差数列是广泛存在的,有很多事物都满足等差数列所描述的规律。掌握等差数列的描述和计算方法,你就能够用数学去描述这些事物。
示例:11 观察图 4 所示的铅笔图样,描述其中的模式。
解: 图 4 中只给出了四个图形,一个合理的猜测是:每次右边的图形都再多摆一个小方块。如果的确如此,那么每个图形的铅笔数恰好构成一个等差数列:\(4,7,10,13,16,...\) 。这是一个首项为 \(4\) 且公差为 \(3\) 的等差数列。 重复模式的图形
重复模式的图形☐
示例: 立方体堆叠:观察如图 5 所示的立方体 (Cubics) 堆叠。你能指出第 10 个这样的堆叠包含多少个小立方块么?
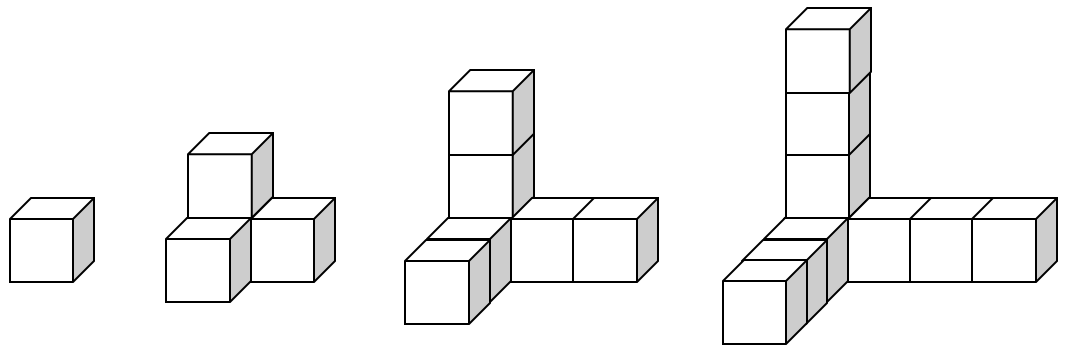 立方体堆叠
立方体堆叠解: 列表使得我们在处理序列问题时拥有清晰的判断力:
请将表中的空白处补充完整,从而得到答案为:\(\_\_\_\_\_\_\_\)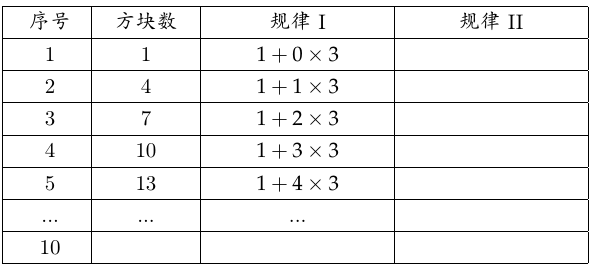 用以处理模式的表格
用以处理模式的表格☐
示例:12 烷烃的分子式:“烷烃” (Alkanes) 是一类有机化合物分子的总称,它由碳原子 (Carbons) 和氢原子 (Hydrogens) 构成。化学家们在表示这种分子时,使用字母 C 表示碳原子,使用字母 H 表示氢原子。分子中碳原子的个数用来给烷烃命名,比如有一个碳原子的烷烃分子被称为“甲烷”,有两个碳原子则被称为“乙烷”,有三个碳原子则被称为“丙烷”,如图 7 所示。观察图中的模式,并回答以下问题:
- [a]. 一百烷 (Hectane) 分子有 100 个碳原子。它有多少个氢原子呢?
- [b]. 烷烃的分子式是 \(C_mH_n\) ,给出 \(m\) 和 \(n\) 的关系。
 烷烃分子式
烷烃分子式计算等差数列(通项公式及其它)
你需要掌握从各个角度计算等差数列的技巧。我们首先引入一些符号来表示等差数列。共有 \(n\) 项的数列可以表示为: \[a_1,a_2,a_3, ..., a_{n-1},a_n\] 也可以替换成别的字母,例如把 \(a\) 替换成 \(b\) ,把表示数列项数的 \(n\) 替换成 \(m\) : \[b_1,b_2,b_3, ..., b_{m-1},b_m\] 习惯上用 \(d\) 表示公差。等差数列 \(a\) 满足: \[\begin{equation} a_k=a_{k-1}+d \end{equation}\]
等差数列的通项公式
为了更加有效地计算等差数列,我们还需要发展更强大的工具。将数列第 \(k\) 项用 \(k\) 表示出来的公式称为通项公式。formula of general term
示例: 烷烃氢原子数列的通项公式:在示例 . 中,氢原子数的序列是 \(4,6,8,10,12,...\) 。可以容易地列出如下表格
根据表格展示的规律,得到通项公式 \(a_k=2k+2\) 。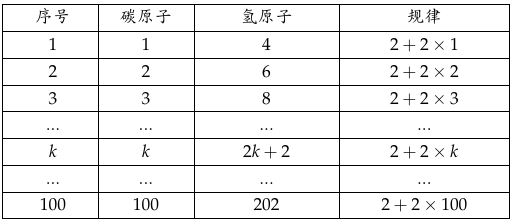 根据题目规律列出表格
根据题目规律列出表格☐
首项为 \(a_1\) 公差为 \(d\) 的等差数列,其通项公式为: \[\begin{equation} a_k=a_1+d\times (k-1) \qquad k=1,2,3,4, ... \end{equation}\]
仅仅有了通项公式还不够,有时候我们需要“反过来”计算。在以下段落,我们继续进行等差数列的推算。
反推等差数列的信息
如果给出等差数列的首项 \(a_1\) 和公差 \(d\) ,再给出一个位置 \(k\) ,我们可以立刻使用通项公式求出该项 \(a_k\) 。但很多情况下,我们有 \(a_k\) 的值,而需要计算 \(a_1\), \(d\) 或 \(k\) 的值。
若等差数列的首项为 \(a_1\) ,第 \(k\) 项为 \(a_k\) ,则公差为: \[\begin{equation} d=\dfrac{a_k-a_1}{k-1} \end{equation}\]
一般地,如果已知两项 \(a_k\) 与 \(a_j\) ,则公差为: \[\begin{equation} d=\dfrac{a_k-a_j}{k-j} \end{equation}\]
若首项为 \(a_1\) ,某项为 \(a_k\) ,公差为 \(d\) ,则该项的序数为: \[\begin{equation} k=\dfrac{a_k-a_1}{d}+1 \end{equation}\]
若第 \(k\) 项为 \(a_k\) ,公差为 \(d\) ,则首项为: \[\begin{equation} a_1=a_k-d\cdot(k-1) \end{equation}\]
思考与讨论
- 你能够直观地看出上述公式的正确性么?
- 你能够通过 推导上述公式么?
- 如果合上书,你能够随时随地写出这几个公式么?
示例: 若等差数列第 \(9\) 项是 \(120\) ,第 \(5\) 项是 \(72\) 。首项是多少?
解: 首先计算公差,我们来套一下公式 : \[d=\dfrac{120-72}{9-5}=12\]
然后再来套一下公式 求首项: \[a_1=72-12\cdot(5-1)=24\]
所以首项为 \(24\) 。☐
数列是 \(24,36,48,60,72,84,96,108,120\)
思考与讨论
- 上面的解法直接套用两次公式,你觉得自然么?
- 如何能够立刻就想到按照这个次序使用公式呢?
- 你有更快的方法计算数列首项么?
示例: 日历间隔问题:淘气的爸爸每工作三天休息一天,妈妈每工作两天休息一天。如果爸爸妈妈同时休息,就带淘气去公园玩。已知 1 月 1 号爸爸妈妈同时休息,问 1 月淘气能去几天公园?
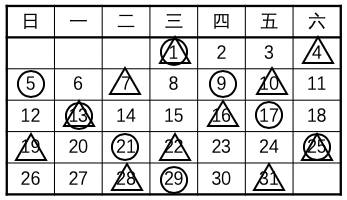 2020 年 1 月日历:在试卷上的原题直接要求学生用记号标记进行求解
2020 年 1 月日历:在试卷上的原题直接要求学生用记号标记进行求解小学三年级上学期试卷中的解法是在日历上画出标记。如图 9 所示,圆圈表示爸爸的休息日,三角表示妈妈的休息日。同时画有三角和圆圈的休息日就是淘气去公园的日子。那请你回答以下问题:
- 找出爸爸妈妈共同休息日的规律;
- 不用逐个计数,找出 2020 年最后一个共同休息日;
- 计算 2020 年的共同休息日数目;
- 如果爸爸妈妈的工作天数分别为 3 和 4 ,那么上述问题答案如何?
- 如果爸爸妈妈的工作天数分别为 4 和 6 ,那么上述问题答案如何?
 2020 年全年日历
2020 年全年日历思考与讨论
如何由爸爸妈妈各自休息日的周期性,计算共同休息日的周期性呢?请注意,简单地做乘法,有时候无法得到最小周期。
等差数列的求和
等差数列求和是课本上的知识。如果已知等差数列的首项、末项和项数,那么数列各项求和的结果应当是:首项加末项,再乘以项数除以 \(2\) 。图 11 展示了在讲述等差数列求和的一个为人津津乐道的例子,相传这是大数学家高斯在上小学时的一道随堂练习。
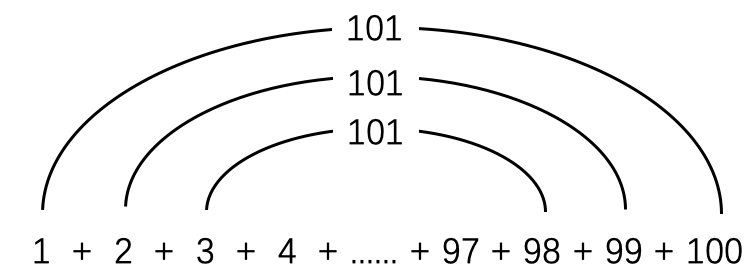 从 1 加到 100 的结果是 \(101\times50=5050\)
从 1 加到 100 的结果是 \(101\times50=5050\)若等差数列共有 \(n\) 项,首项为 \(a_1\) ,末项为 \(a_n\) ,则数列求和公式如下: \[\begin{equation} \sum_{i=1}^{n}a_i=\dfrac{(a_1+a_n)\cdot n}{2} \end{equation}\] 其中 \(\sum_{i=1}^{n}a_i\) 是求和记号(参见图 ),表示对 \(a_i\) 求和, \(i\) 取遍 1 到 \(n\) 。
 求和符号:\(\sum\) 下方的 \(n=1\) 表示求和项中 \(n\) 是变化的,从 \(1\) 开始。上方的 \(4\) 表示 \(n\) 的截止数值是 \(4\)
求和符号:\(\sum\) 下方的 \(n=1\) 表示求和项中 \(n\) 是变化的,从 \(1\) 开始。上方的 \(4\) 表示 \(n\) 的截止数值是 \(4\)示例: 写出以下求和符号对应的数列,并求出数列和。 \[\sum_{i=1}^{100}i\qquad \sum_{i=0}^{20}1+2i\qquad \sum_{i=1}^{10}10-i\qquad \sum_{i=1}^{5}i^2\]
解: 前三个是等差数列,可以使用公式求和。最后一个是平方数序列,直接计算求和。\[\sum_{i=1}^{100}i=1+2+3+4...+100=\dfrac{(1+100)\cdot100}{2}=5050\] \[\sum_{i=0}^{20}1+2i=1+3+5+...+41=\dfrac{(1+41)\cdot21}{2}=441\] \[\sum_{i=1}^{10}10-i=9+8+7+...+1+0=\dfrac{(9+0)\cdot10}{2}=45\] \[\sum_{i=1}^{5}i^2=1+4+9+16+25=55\]平方数序列求和也是有公式的,这超出了本章的论述范围。
☐
示例: 已知首项、公差和项数,如何求等差数列的和呢?
解: 在求解没遇见过的问题时,你可以尝试以下步骤:只需要通过公差和项数计算出末项即可。在进行一般性的推导前,计算一个具体的例子,比如 \(1+4+7+10+...\) 共 10 项。- 如果无法直接求解,可以尝试将题设条件转换为已知模式;
- 设计几个具体的例子,用以辅助思路和测试解题方案;
从特殊情形开始
这是一个首项为 1 ,公差为 3 ,项数为 10 的等差数列。容易计算末项为 \(1+3\times(10-1)=28\) 。于是我们可以利用等差数列求和公式计算出数列的各项和为: \[\dfrac{(1+(1+3\times(10-1)))\times10}{2}=\dfrac{(1+28)\times10}{2}=145\]
接下来只需将首项 1 替换为 \(a_1\) ,公差 3 替换为 d ,项数 10 替换为 n,就可以推导出一般性结论。对于首项为 \(a_1\) ,公差为 \(d\) ,项数为 \(n\) 的一般性等差数列,我们就很容易推导末项等于:容易验证,上述结果和直接对 \(1,4,7,10,13,16,19,22,25,28\) 求和的结果一样。
用字母表示一般情形
\[a_n=a_1+d\cdot(n-1)\] \[\sum_{i=1}^{n}a_i=\dfrac{(a_1+a_n)\cdot n}{2}=\dfrac{(a_1+a_1+d\cdot(n-1))\cdot n}{2}=n\cdot a_1+\dfrac{(n-1)n}{2}\cdot d\]
因此我们的到结论:
设等差数列的首项为 \(a_1\) ,公差为 \(d\) ,项数为 \(n\) ,则等差数列的和为: \[\begin{equation} S=n\cdot a_1+\dfrac{(n-1)n}{2}\cdot d \end{equation}\]
☐
思考与讨论
- 写出几个具体的等差数列,在已知 \(a_1,d,n\) 但不知道末项 \(a_n\) 的情况下,测试一下上述求和公式的正确性;
- 你能够用直观的方式解释公式 的正确性么?\ (参见习题 B.)
- 已知首项、末项和公差,如何求等差数列的和?
示例: 证明从 1 开始的自然数奇数序列的和是项数的平方。 \[\begin{equation*} \begin{aligned} 1 \quad &= \quad 1 &= \quad 1^2\\ 1 + 3 \quad &= \quad 4 &= \quad 2^2\\ 1 + 3 + 5 \quad &= \quad 9 &= \quad 3^3\\ 1 + 3 + 5 + 7 \quad &= \quad 16 &= \quad 4^2 \end{aligned} \end{equation*}\]
- [a]. 观察上面算式的规律,再写几个验证一下;
- [b]. 用求和记号写出一般化的结论;
- [c]. 如何证明该结论呢?证明一个数学命题往往有多种方法。研究这些不同的方法是非常有价值的,这能极大地丰富我们的数学技能库。131415
 几何证明
几何证明将形数序列转化为等差数列求解
有些数列虽然本身不是等差数列,但也可以将其转化为等差数列求解。考虑如下问题:
示例: 三角形阵列:在图 14 中,对组成三角形阵列图形序列的小木棒(线段)进行计数,得到序列 \(3,9,18,30,45,...\) 。求该序列的第 100 项,即图 所示的图形中的线段数目
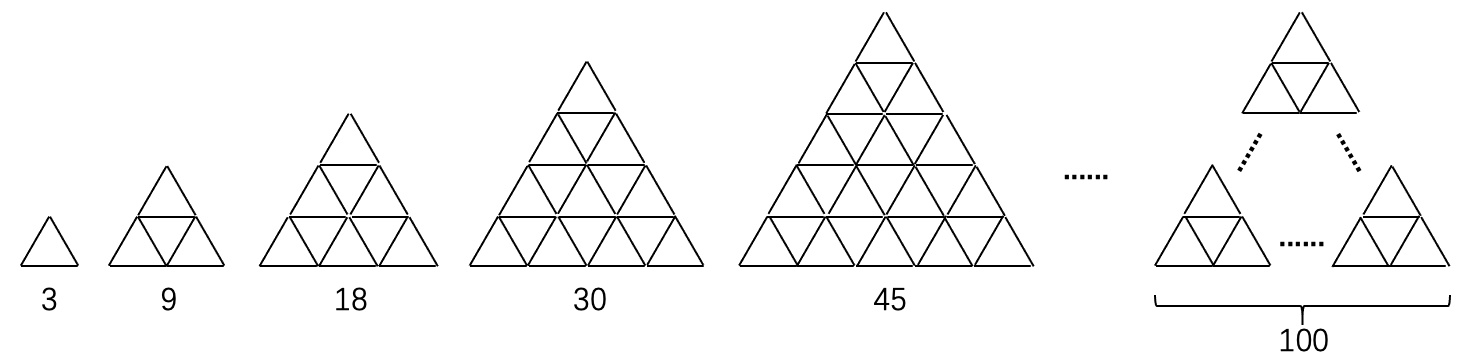 三角形阵列
三角形阵列解法一 观察三角形阵列,发现其可以如图 15 所示拆分。
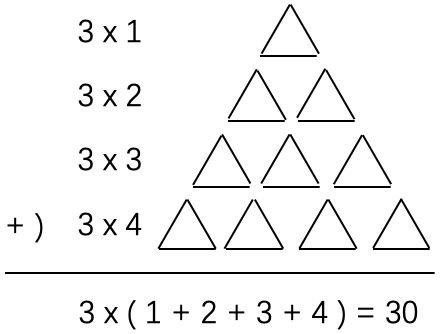 序列的规律
序列的规律根据图 15 的模式,边长为 100 的三角形阵列的线段数为: \[3\times\sum_{i=1}^{100}i=3\times5050=15150\]
即序列 \(3,9,18,30,45,...\) 的第 100 项为 15150 。☐
解法二 在前述解法中,利用了图形的性质,将求某一项的问题转换为等差数列求和问题。如果没有图形辅助,这一规律不容易直接看出。我们可以将数列相邻两项做差观察到等差数列的存在:
于是数列的第 100 项等于 \(3+(6+9+12+15+...)\) ,其中括号里是首项为 6 公差为 3 共计 99 项的等差数列的和。我们可以计算出该等差数列的末项为 300 。故三角形阵列线段数列第 100 项为: \[3+(6+9+12+15+...+300)\]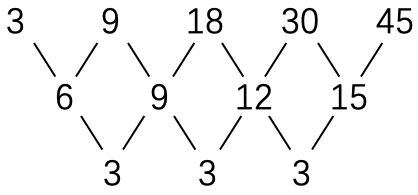 序列的规律应用等差数列求和公式得到 15150 。
序列的规律应用等差数列求和公式得到 15150 。注意到恰好 3 放进来也是等差数列,所以计算很容易
☐
思考与讨论
- 你能写出三角形阵列数列的通项公式么?
- 你能写出该数列的前 \(n\) 项和的公式么? \(\bigstar\bigstar\)
等差数列的应用
示例: (鸡兔同笼问题)笼子里有鸡和兔子共 \(10\) 只,腿共 \(34\) 条。问鸡兔各几只?
解: 题目有两个条件“共 \(10\) 只”和“共 \(34\) 条腿”。我们先尝试着满足第一个条件:假设 \(10\) 只动物都是鸡,没有兔子。这显然无法满足第二个条件,因为腿总共只有 \(20\) 条。于是我们要把一些鸡换成兔子。每次将 \(1\) 只鸡换成兔子,腿会增加两只。不断增加兔子的过程如表 所示:
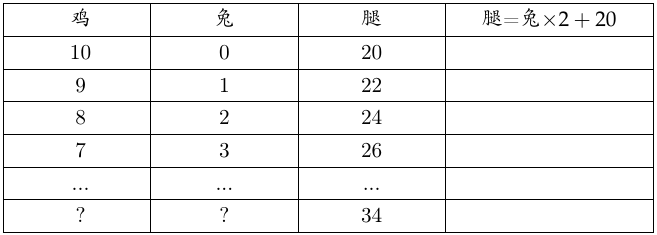 动物的数量和腿数的变化规律
动物的数量和腿数的变化规律我们只要找到标记问号的一行应该填入什么数字即可。于是问题转换为:\(1\) 只兔子,腿 \(22\) 。每次增加 \(1\) 只兔子,增加两条腿。多少只兔子时,腿有 \(34\) 条?
这是一个已知等差数列首项、公差和末项,求项数的问题:项数等于末项减首项,除以公差再加一
即:已知 \(a_1=22, \quad d=2, \quad a_n=34\) , 求 \(n\) 。 \[n=\dfrac{a_n-a_1}{2}+1=\dfrac{34-22}{2}+1=7\]
因此我们知道有 \(3\) 只鸡 \(7\) 只兔子。
验算:将 \(3\) 和 \(7\) 代入题意:\(3\times2+7\times4=34\) ,相符。☐
示例: (百僧百馍问题)一百个僧人共吃一百个馒头,大僧每人吃三个,小僧每三人吃一个,问大僧小僧各有多少人?
解: 题目乍一看不会做,那么看看能不能去掉一些条件,让题目变得更简单些。题目有 3 个条件:
- [1.] 大僧小僧共 100 人;
- [2.] 大僧 1 人吃 3 个馒头,小僧 3 人吃 1 个馒头;
- [3.] 共吃了 100 个馒头。
我们就看第一个条件“共 \(100\) 人”。不妨随便取一些数字,看馒头能吃多少?大僧 \(100\) 人,小僧 \(0\) 人,算一下吃 \(300\) 个馒头(100x3=300)。显然馒头太多了,需要把一些大僧换成小僧。换多少呢?如果只换一个小僧,你会发现馒头不是整数。所以我们要 \(3\) 人 \(3\) 人换。
- [] 大僧 \(97\) 人,小僧 \(3\) 人,算得吃 \(292\) 个馒头(\(97\times3 + 1 = 292\))
- [] 大僧 \(94\) 人,小僧 \(6\) 人,算得吃 \(284\) 个馒头(\(94\times3 + 2= 284\))
- [] …
找规律发现每次换 \(3\) 个和尚,就少吃 \(8\) 个馒头。那换多少次,才能让馒头数从 \(300\) 降到 \(100\) 呢?显然要换 \(200/8=25\) 次。
于是总共要换 \(25 \times 3 = 75\) 个和尚,才能让馒头数正好是 \(100\) 。因此答案为小僧 \(75\) 人 ,大僧 \(25\) 人。
验算:\(25x3+75/3=100\) 个馒头,与题意相符。☐
思考与讨论
- 请写出我们在求解“百僧百馍”问题时等价的等差数列问题。
- 你以前听说过“鸡兔同笼”和“百僧百馍”问题么?你还知道什么解法?
- 修改上述“鸡兔同笼”和“百僧百馍”的条件数据(比如将 \(34\) 条腿修改为别的数字),问题仍然有解么?
- 进行一般性讨论,在什么条件数据下,上述问题有解?
示例: (和差问题)两个数的和是 \(56\) ,其差是 \(14\) 。问两数各是多少?
解: 先考虑“和是 \(56\)”这个条件。比如一个数是 \(56\) ,另一个数是 \(0\) 。我们看一看差是如何变化的,如表 18 所示:
有了前面的经验,我们可以计算出数 \(2\) 应为:\((56-14)\div2=16\) ,从而数 \(1\) 为 \(56-16=40\) 。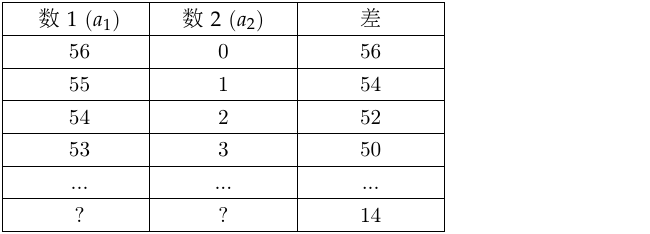 和为 \(56\) 的两数之差变化规律
和为 \(56\) 的两数之差变化规律☐
思考与讨论
- 你还有什么办法求解“和差问题”?
- 如果你想不出别的办法,利用互联网检索一下。
- 你的办法列出的算式和示例的求解过程有何同异?
示例: (和倍问题)两个数 \(a,b\) 之和为 \(56\) , \(a\) 为 \(b\) 的 \(3\) 倍。求 \(a,b\) 的值。
解: 我们先固定第二个条件“ \(a\) 为 \(b\) 的 \(3\) 倍”。然后变化 \(b\) ,看看二者之和是如何变化的:
{和为 \(56\) 的两数之差变化规律}
请读者将剩下的步骤自行补充完整:
示例: (差倍问题)两个数 \(a,b\) 之差为 \(56\) , \(a\) 是 \(b\) 的 \(3\) 倍。求 \(a,b\) 的值。
等比数列(选学)
等比数列 (Geometric Squences) 的每一项都等于其前项乘以一个固定的非零值。这个固定的乘数被称为“公比” (ratio) 。
- \(2,4,8,16,32,...\) ,这是一个公比为 \(2\) 的等比数列;
- \(5,5,5,5,5,5\) 也是等比数列,它的公比是 \(1\) ;
为了方便地标记等比数列,我们来介绍一下指数运算:
指数运算
- 如果 \(n\) 是自然数,则 \(a^n=\overbrace{a\cdot a \cdot a ... \cdot a}^{n factors}\) ;
- 如果 \(n=0\) 且 \(a\neq0\) ,则 \(a^n=1\) ;
\(a^n\) 念作“ \(a\) 的 \(n\) 次方”或者“** \(a\) 的 \(n\) 次幂**”。a 称为“底数”, n 称为“指数”,运算的结果称为“幂” 。特别地,\(a^2=a\cdot a\) 称为 “\(a\) 的平方”, \(a^3=a\cdot a\cdot a\) 称为 “\(a\) 的立方”。 \(n\) 不仅限于非负整数,你会在中学数学课程中遇到完整的指数运算
示例: 将等比数列 \(1,2,4,8,16,32,64,128,256,512,1024\) 的和写成 \(\sum\) 记号的形式,并计算结果。
解: 这个数列的求和用指数记号表示如下所示: \[\sum_{i=0}^{10}2^i=2^0+2^1+2^2+ ... + 2^{10}\]
将上述求和等式两边同时乘以 2 ,如图 20 所示。
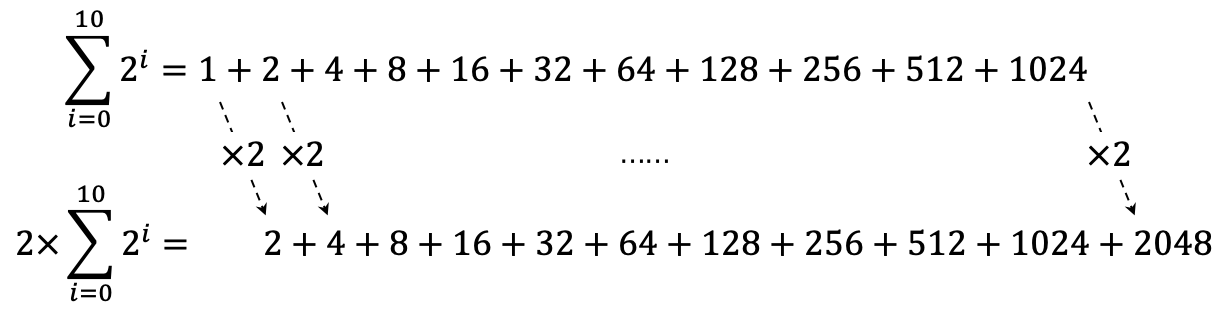 等比数列求和-I
等比数列求和-I再用新得到的等式减去原来的等式,如图
即求和结果等于 \(2^11-1=2047\) 。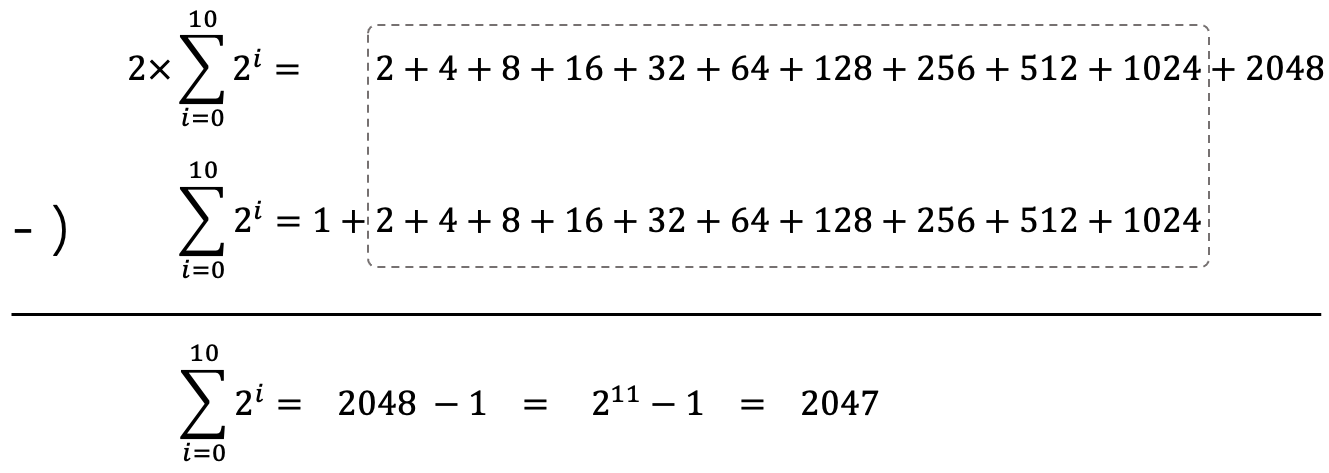 等比数列求和-I
等比数列求和-I☐
思考与讨论
- 你能够直观看出上述示例的结论么?
- 你能够将上述示例的结论推广至一般化的等比数列么?
如果你是初次见到等比数列,那你一定会惊叹于它带来的快速增长。请看如下问题:
示例: 相传古印度王国的宰相达依尔发明了国际象棋。国王非常喜爱这个游戏,一天他在完成一盘对局之后高兴地对达依尔说:“我亲爱的宰相啊,为了奖励你的伟大发明,本王决定满足你的一个任何要求。”
宰相恭敬地答道:“我尊敬的陛下啊,您的恩典对我就像恒河水之于水稻,就像大地之于人民,我怎敢提出过分的要求呢。臣只有一个很小的要求,请您在棋盘的第一个方格放上 \(1\) 粒米,第二个方格放上 \(2\) 粒米,第三个方格放上 \(3\) 粒米,之后每一个方格的米粒数是前一个方格的两倍,放满棋盘上的 \(64\) 个方格,总共这些米就是我要的奖赏。”
国王很是疑惑,但仍郑重说道:“聪明的宰相啊,你为什么只要求这么少的奖赏呢?既然如此,本王尊重你的意愿,我将为这次奖励举行一个隆重的仪式。”
国王亲自主持了一开始的摆米仪式,他在第一个格子摆了 \(1\) 粒米,然后是 \(2\) 粒米、 \(4\) 粒米、 \(8\) 粒米、 \(16\) 粒米。摆完 \(5\) 个格子后,国王就回宫了,剩下的仪式由你负责主持,请回答如下问题:
 国王和大臣
国王和大臣- [a]. 接下里的 5 个格子分别要摆多少米粒;
- [b]. 国王一共要奖赏大臣多少米?
- [c]. 第 64 个格子要摆多少米粒,写成乘方的形式;
- [d]. 请你估计一下第 64 个格子米粒数的位数,并说明理由;
- [e]. 使用计算器或者计算机,计算第 64 个格子的米粒数;
解:
- 接下来的五个格子分别要摆 32 、 64 、 128 、 256 和 512 粒米。
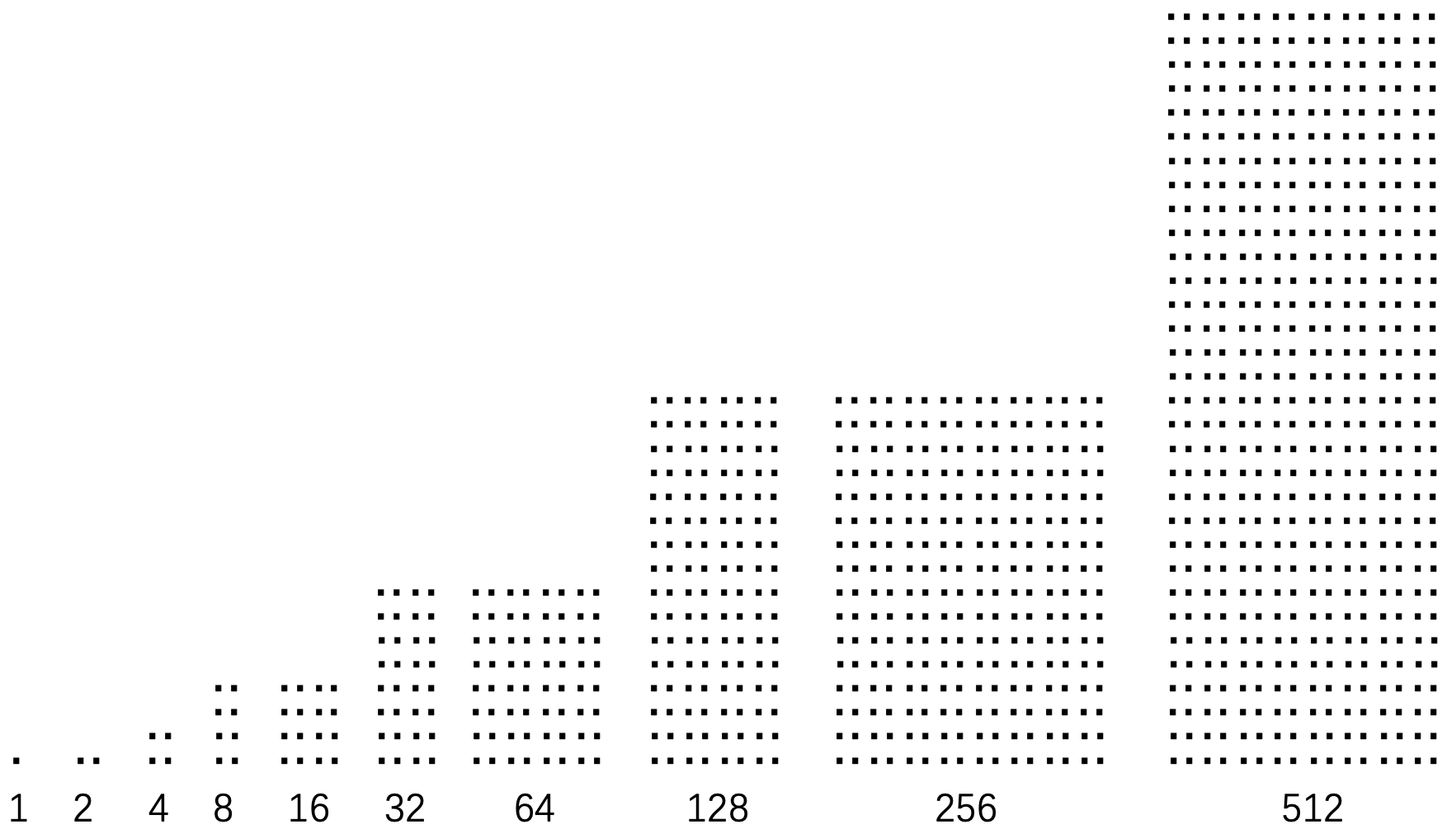 前 10 个格子的米粒数
前 10 个格子的米粒数有了前面示例的结论,我们可以很容易地写出国王一共需要赏赐 \(2^65-1\) 粒米。
把格子的米粒数写成 2 的乘方: \begin{enumerate}
- [1]. 第 1 个格子里的米粒数是 \(2^0\) 粒;
- [2]. 第 2 个格子里的米粒数是 \(2^1\) 粒;
- [3]. 第 3 个格子里的米粒数是 \(2^2\) 粒;
- [.]. ……
- [n]. 第 \(n\) 个格子里的米粒数是 \(2^{n-1}\) 粒; \end{enumerate}
因此第 64 个格子里有 \(2^{63}\) 粒米。
- 我们沿着第一问再计算出一项 \(2^{10}=1024\) ,然后试图使用 1000 代替 10 个 2 相乘的结果: \[2^{63}=2^{10}\cdot2^{10}\cdot2^{10}\cdot2^{10}\cdot2^{10}\cdot2^{10}\cdot2^3\approx1000^6\cdot8\] 估算的结果为 8000000000000000000 ( 8 后面 18 个 0 )。更准确的估计方法则要等到学习了二项式展开: \[1024^6\cdot8=(1000+24)^6\cdot8\approx(1000^6+6\cdot24\cdot1000^5)\cdot8\] 估算的结果为 9152000000000000000 ( 9152 后面 15个 0 )。
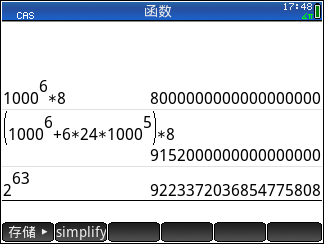 用计算器计算方幂
用计算器计算方幂- 使用惠普图形计算器的计算结果如图 24 所示,可见取二项式展开的前两项的估计还是比较准确的。
☐
随堂练习 1
练习:16 Sophie 用火柴棍摆了十个房子,图 25 画出了这一排房子的前四个。请问 Sophie 摆这十个房子总共用了多少根火柴?
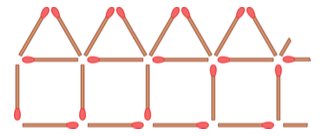 火柴房子
火柴房子练习: 五个小朋友排成一列玩击鼓传花游戏。刚开始时,花球在第一位小朋友手里。开始击鼓后,花球被不断传递至下一个人手中,传到队伍尽头时,再往回传递。鼓声停止时,传递了 100 次,此时花球在谁的手里?
练习: 如图 26 ,有一堆按规律摆放的砖。从上往下数,第 1 层有 1 块砖,第 2 层有 5 块砖,第 3 层有 9 块砖。按照这样的规律,第 19 层有多少块砖?
 砖墙
砖墙练习: 等差数列综合计算
- [a.] 等差数列有 13 项,后项比前项大 2 ,首项为 33 ,末项是多少?
- [b.] 等差数列有 13 项,后项比前项小 2 ,首项为 33 ,末项是多少?
- [c.] 等差数列有 10 项,后项比前项大 7 ,末项为 125 ,首项是多少?
- [d.] 等差数列有 10 项,后项比前项小 7 ,末项为 125 ,首项是多少?
- [f.] 等差数列第 4 项为 7 ,第 10 项为 61 ,公差是多少?
- [g.] 等差数列首项为 5 ,末项为 93 ,公差为 8 ,项数是多少?
- [h.] 等差数列第 3 项为 50 ,末项为 130 ,公差为 8 ,项数是多少?
练习: 已知等差数列第 4 项等于 31 ,第 10 项等于 73 。
- [a.] 公差是多少?
- [b.] 493 在数列中么,如果不在说明理由,如果在是第几项?
练习: 按规律写出一列算式:\(1000-1\) , \(993-4\) , \(986-7\) , \(979-10\) 。如果要保证被减数比减数大,最多能写出几个算式?请写出最后的算式。练习: 笼子里共有鸡和兔子 \(50\) 只,腿共 \(124\) 条。问鸡和兔子各几只?练习: 小薯片 \(5\) 元钱一包,大薯片 \(8\) 元钱一包。\(500\) 元钱恰好买了 \(73\) 包薯片。请问大小薯片各买了多少包?练习: 你有黑色和白色棋子共 \(20\) 个,黑色棋子比白色棋子多 \(4\) 个。问黑白棋子各有多少个?练习: 你有黑色和白色棋子共 \(150\) 个,黑色棋子是白色棋子的两倍多 \(5\) 个。问黑白棋子各有多少个?习题 1A
A 类习题和 B 类习题题目类似,但容易一些。
问题: 观察如下样式,求 \(1+50\cdot51\cdot52\cdot53=\triangle^2\) 中 \(\triangle\) 的值。
\[\begin{equation} \begin{aligned} 1+1\cdot2\cdot3\cdot4&=5^2 \\ 1+2\cdot3\cdot4\cdot5&=11^2 \\ 1+3\cdot4\cdot5\cdot6&=19^2 \\ 1+4\cdot5\cdot6\cdot7&=29^2 \end{aligned} \end{equation}\]
问题: 观察以下数列的模式,再写出三项。指出它们是等差还是等比数列。
- [a.] 1, 3, 5, 7, 9 ;
- [b.] 0, 50, 100, 150, 200 ;
- [c.] 3, 6, 12, 24, 48 ;
- [d.] 10, 100, 1000, 10000, 100000 ;
- [e.] 9, 13, 17, 21, 25, 29 ;
问题: 计算以下算式的结果:
- [a.] \(1+2+3+4+...+98+99\) ;
- [b.] \(1+3+5+7+...+1001\) ;
- [c.] \(36+37+38+...+137\) ;
问题: 写出前 \(n\) 个自然数的求和公式,并且用图 27 解释你写出的公式。
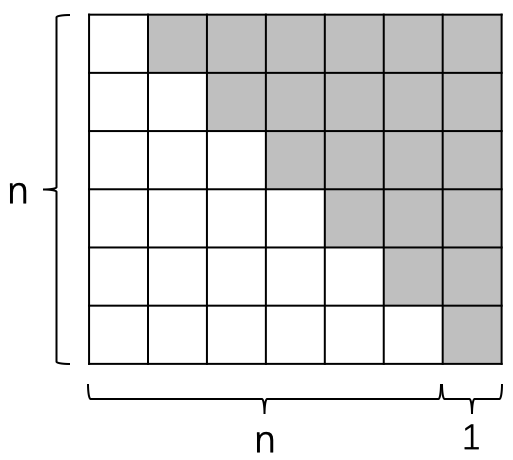 \(1+2+...+n\) 求和的几何解释
\(1+2+...+n\) 求和的几何解释问题: 不对数列求和,指出 \(O\) 和 \(E\) 哪个结果比较大,大多少。 \[O=1+3+5+7+...+97\] \[E=2+4+6+8+...+98\]
问题: 序列 \(1,6,11,4,9,...\) 是在表盘上的时针每次前进 \(5\) 个小时的时针指向位置。即 \(1\) 点再过 \(5\) 个小时是 \(6\) 点, \(6\) 点再过 \(5\) 个小时是 \(11\) 点, \(11\) 点再过 \(5\) 个小时是 \(4\) 点,依次类推。回答如下问题:
- [a.] 将上述序列再写出 \(3\) 项;
- [b.] 时针每次前进 \(5\) 个小时,能走遍所有的整点么;
- [c.] 写出时针每次前进 \(8\) 个小时的序列,能走遍所有的整点么?
- [d.] 时钟每次前进 \(100\) 个小时,能走遍所有的整点么?\(\bigstar\)
问题: \(1, 8, 27, 64, 125, ...\) 是立方数 (cubic) 序列。其中 \(a_n=n^3\) ,即 \(a_1=1^3\) , \(a_2=2^3\) 。
- [a.] 再写出立方数数列的三项;
- [b.] 数列中最小的 \(4\) 位数是什么?
- [c.] 将数列相邻两项相减,得到一个新数列。将新得到的数列相邻两项再相减再得到一个数列。第二次相减操作的得到的数列是什么数列?
问题: 等比数列 \(1,a,a^2,a^3,a^4,...\) 也被称作乘方数序列。
- [a.] 研究数列 \(8^1,8^2,8^3,8^4,....\) 的个位数出现模式, \(8^{100}\) 的个位数是多少?
- [b.] 研究上述数列各项除以 \(3\) 的余数模式,\(8^{100}\) 除以 \(3\) 的余数是多少?
习题 1B
B 类习题与 A 类题目类似,但难一些。
问题: 观察如下样式,解答问题。 \[\begin{equation} \begin{aligned} 1+1\cdot2\cdot3\cdot4&=5^2 \\ 1+2\cdot3\cdot4\cdot5&=11^2 \\ 1+3\cdot4\cdot5\cdot6&=19^2 \\ 1+4\cdot5\cdot6\cdot7&=29^2 \end{aligned} \end{equation}\]
- [a.] 求 \(1+50\cdot51\cdot52\cdot53=\triangle^2\) 中 \(\triangle\) 的值;
- [b.] 用 \(n\) 写出一般性的规律;
- [c.] 证明你发现的规律;\(\bigstar\bigstar\)
问题: 写出等差数列的求和公式,用图 28 解释该公式。
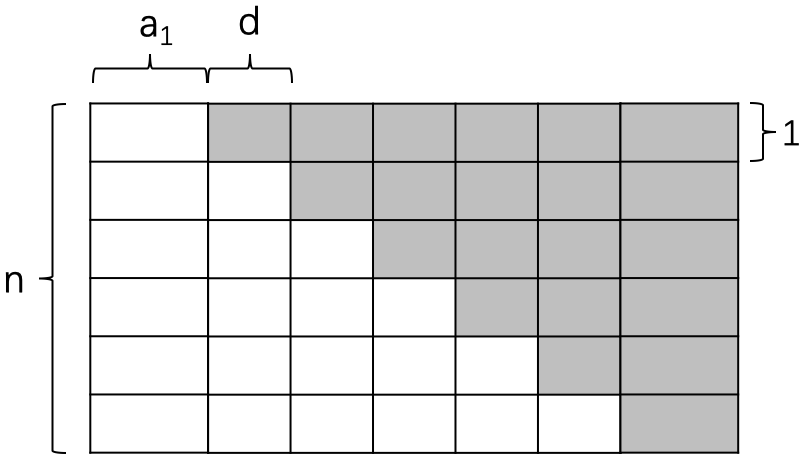 等差数列求和的几何解释
等差数列求和的几何解释问题: 不对数列求和,指出 \(O\) 和 \(E\) 哪个结果比较大,大多少。 \[O=1+3+5+7+...+97\] \[E=2+4+6+8+...+96\]
问题: 序列 \(1,6,11,4,9,...\) 是在表盘上的时针每次前进 \(5\) 个小时的时针指向位置。即 \(1\) 点再过 \(5\) 个小时是 \(6\) 点, \(6\) 点再过 \(5\) 个小时是 \(11\) 点, \(11\) 点再过 \(5\) 个小时是 \(4\) 点,依次类推。回答如下问题:问题:\(1, 8, 27, 64, 125, ...\) 是立方数 (cubic) 序列,其中 \(a_n=n^3\) 。
- [a.] 数列中最小的 \(5\) 位数是什么?
- [b.] 将立方数数列相邻两项相减,得到一个新数列。将新得到的数列相邻两项再相减再得到一个数列。第二次相减操作的得到的数列是什么数列?
- [c.] 四次方数列 \(1^4,2^4,3^4,4^4,...\) 进行上述相减操作几次后,能得到类似的数列?
- [d.] 对等比数列进行上述相减操作几次后,能得到类似的数列?
问题: 等比数列 \(1,a,a^2,a^3,a^4,...\) 也被称作乘方数序列。
- [a.] 研究数列 \(7^0,7^1,7^2,7^3,7^4,....\) 的个位数出现模式, \(7^{100}\) 的个位数是多少?
- [b.] 研究上述数列各项除以 \(5\) 的余数模式,\(7^{100}\) 除以 \(5\) 的余数是多少?
习题 1C
C 类题目是提高习题,数学竞赛级别。
问题: 五边形数是如图 29 所示图形序列的形数。我们把这个序列 \(1, 12, 22, 35, ...\) 称为“五边形数序列”
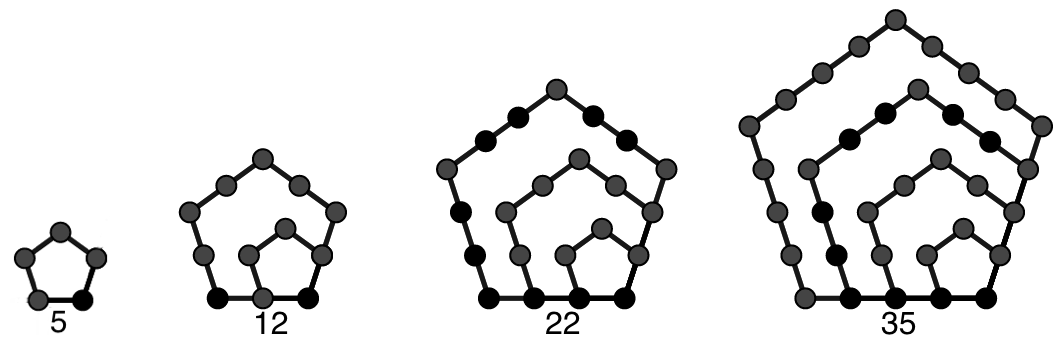 五边形数
五边形数- [a.] 根据图中规律,再写出两个五边形数;
- [b.] 五边形数序列可以通过逐项做差得到等差数列么?
- [c.] 第 \(20\) 个五边形数是多少?
- [d.] 推导五边形数序列的通项公式;
问题: 冰雹猜想是指:一个正整数 \(x\) ,如果是奇数就乘以 \(3\) 再加 \(1\) ,如果是偶数就除以 \(2\) ,这样经过有限次,一定能够得得到 \(1\) 。例如数字 \(10\) 的变换: \[\begin{equation} \begin{aligned} 10\div 2&=5\\ 5\times3+1&=16\\ 16\div2&=8\\ 8\div2&=4\\ 4\div2&=2\\ 2\div2&=1 \end{aligned} \end{equation}\]
- [a.] 针对 \(20\) 以内的正整数,验证冰雹猜想;
- [b.] 如果你学习过编程,写一个验证冰雹猜想的程序;
问题: 杨辉三角形,又称帕斯卡三角形。是如下排布成三角形的一组数:
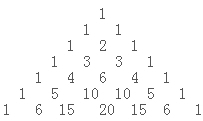 杨辉三角形
杨辉三角形这个三角形数表在我们后面的学习中(排列组合、二项式展开)会起到很大作用。在这个阶段,我们仅仅把它当做数列练习来做。
- 观察这张数表,你能发现什么规律?
- 补充这张数表,续写两行。
问题: 斐波那契数列 (Fibonacci sequence) ,是法国数学家列昂纳多·斐波那契 (Leonardoda Fibonacci) 以兔子繁殖为例子而引入的数列。该数列从第 \(3\) 项开始,每一项都等于前两项之和。 \[1, 1, 2, 3, 5, 8, 13, 21, 34, ......\]
- [a.] 根据规律,再写出 \(5\) 项;
- [b.] 图 31 展示的鹦鹉螺的螺旋线里隐藏着斐波那契数列,你能看出来么?
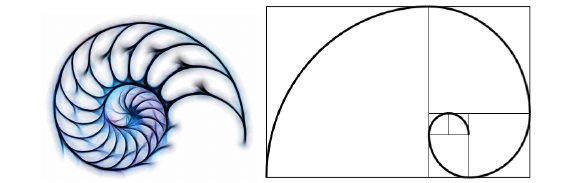 鹦鹉螺的螺旋线
鹦鹉螺的螺旋线- [c.] 请你把以下数列按增长速度排序。从增长速度上,斐波那契数列更像哪个? \[1,2,3,4,5,...\] \[1,2,4,8,16,...\] \[1,4,9,16,25,...\] \[1,8,27,64,125,...\]
- [d.] 斐波那契数列的通项公式不是那么直观,查阅资料找到其通项公式的表述。
问题:17 粗心的洋洋想要计算“\(1+2+3+...+n\)”的和,但他不慎把其中一个数加了两次,结果得到了 \(1000\) 。那么洋洋把哪个数加了两次? \(n\) 等于多少?