基础知识

基础知识

用符号进行运算

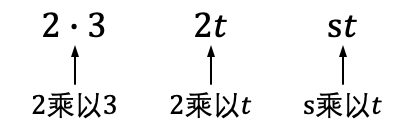
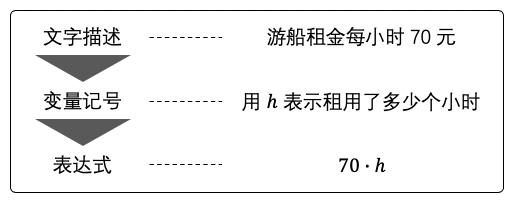
数学家使用代数符号描述普遍性的规律。符号可以用来代表某个数字。例如，表达式 \(2+n\) 代表 \(2\) 与某个数字的和。代数表达式是变量、符号和运算符的组合。为了避免和字母 \(X\) 混淆，我们使用点号表示乘法，或者干脆不写乘法记号。如图 1 所示。

乘法记号

你应当精心挑选符号，因为那样利于数学算式的阅读。例如，常常使用字母 \(x,y,z\) 来表示未知量，而使用 \(m,n\) 表示自然数。使用英文首字母也是不错的选择，比如用 \(w\) 表示宽度 (Width) ， \(l\) 表示长度 (Length) ， \(h\) 表示高度 (Height) 。

思考与讨论

对代数表达式求值

用给定数字替代表达式中的字母，完成替代后，你就可以对表达式求值（计算表达式的值）。

示例： 根据给出的变量值，计算表达式的值： \[\begin{equation*} \begin{aligned} 16+b\qquad &b=25\\ x-y\qquad &x=64,y=27 \end{aligned} \end{equation*}\]

解： 用给出的变量值替代对应的变量符号进行计算： \[\begin{equation*} \begin{aligned} 16+\boxed{b}&=16+\boxed{25}\\ &=41 \end{aligned} \end{equation*}\]

\[\begin{equation*} \begin{aligned} x-y&=64-27\\ &=37 \end{aligned} \end{equation*}\]

☐


为实际问题建立数学模型

数学家喜欢使用代数来表示事物之间的关系。一旦得到了代数表达式，我们就为实际问题建立了“数学模型”。这些“数学模型”是解决问题的核心所在。

示例： 公园门票 7 元，公园里的旋转木马一次 2 元。一位小朋友在周末坐 \(t\) 次 (times) 旋转木马的花费 (costs) 是 \(C=7+2t\) 。根据代数表达式，计算周末去坐 5 次旋转木马的花费。

示例： 通过外卖软件买冰棒，一根冰棒 \(2\) 元，一次快递收费 \(7\) 元。写出一次买 \(n\) 根冰棒花费的表达式。并计算一次购买 \(5\) 根冰棒的花费。

上述两个示例说明，不同的实际问题可以对应同样的数学模型 (\(y=7+2x\)) 。运用数学解决问题有两个层面：

这二者缺一不可，在学习中都要注意。

示例： 一个三角形的底边长度为 \(b\) ，它的高比底边长 \(3cm\) ，则该三角形的面积为 \((b+3)\cdot b/2\) 。请问底边长度为 \(8cm\) 的三角形的面积是多少？

你也许还没有学过什么叫三角形的底边和高，也不知道三角形的面积的计算方法。但这不影响你解决本问题。

A. \(20 cm^2\) \(\qquad\) B. \(25 cm^2\) \(\qquad\) C. \(44 cm^2\) \(\qquad\) D. \(88 cm^2\)

请按照以下步骤解决问题：

随堂测验 1

\(m=4\), \(z=9\) 求下列表达式的值：

\(3+m\) \(\qquad\) \(z+5\) \(\qquad\quad\) \(z-m\)

\(m-2\) \(\qquad\) \(4m-2\) \(\qquad\) \(2z+3\)

随堂测验 2

你兜里有 \(20\) 元钱，你要买 \(4\) 根冰棍。如果一根冰棍是 \(p\) 元钱，那么买完后你还剩下 \(20-4p\) 元。如果冰棍 \(3\) 元一根，你还剩下多少钱？

函数

函数将给定的输入经过计算，得到一个结果。函数描述了输入和输出之间的关系。

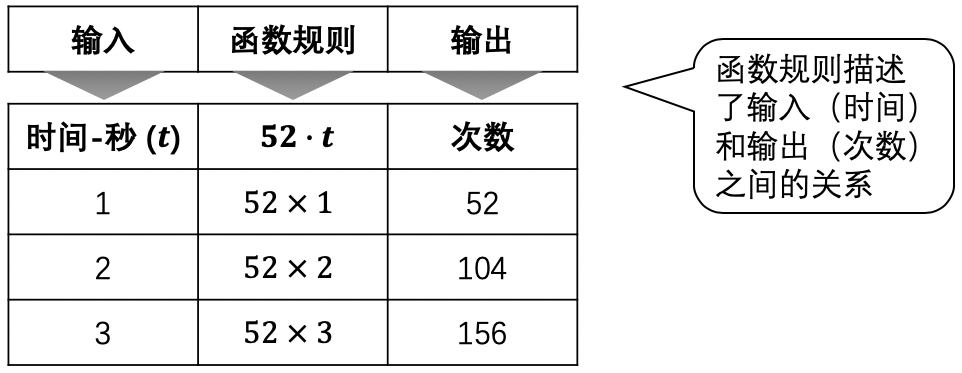
示例： 一只蜂鸟每秒钟扇动翅膀 \(52\) 次。在一段时间间隔 \(t\) 秒中，蜂鸟扇动翅膀的次数是 \(52\cdot t\) 次。图 2 给出了这种关系的一些数值。

蜂鸟扇动翅膀次数和时间的函数关系

示例： 仿照表 中左上角的表格，将空白的表格补充完整。

根据函数关系计算，或者根据数据确定函数关系

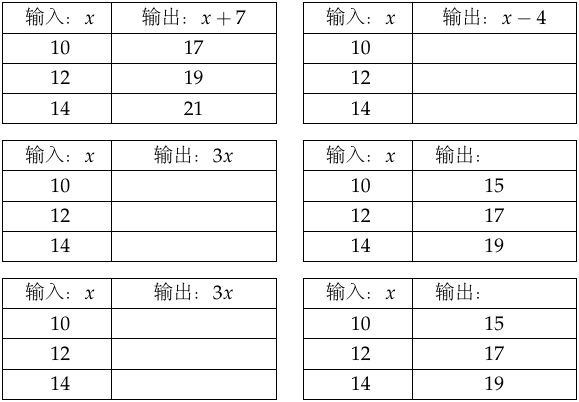
示例： 公园里的游船每小时的租金是 \(70\) 元。定义一个变量表示划船时间，然后写出表示总租金和划船时间关系的函数表达式。

从文字描述到代数表达式的过程

运算符、优先级和结合性

“先加减后乘除”，其中的“加减乘除”就是运算符，“先后”就是指优先级。本节我们将仔细讨论运算符的性质。

运算数、运算符和表达式

表达式由运算数和运算符组成。例如 \(6+3\) 中，\(6\) 和 \(3\) 是运算数， \(+\) 是运算符。表达式的计算结果称为表达式的值。

上述关于表达式的定义很粗糙，严格地来说，单个运算数也是表达式，表达式可以组合出更加复杂的表达式，表达式中还可以包含括号。

思考与讨论

在三年级上学期 ，我们学到“混合运算”。对含有多个运算符的表达式求值时，例如 \(6+3\times2\) ，就需要优先级和结合性规则。

优先级

当表达式中出现多个运算符时，先计算优先级高的，后计算优先级低的。

结合性

当表达式中出现多个同级别运算符时，结合性指明了运算次序。一般来说，运算符的结合性是从左到右，称为“左结合性”。反之，则称为“右结合性”。

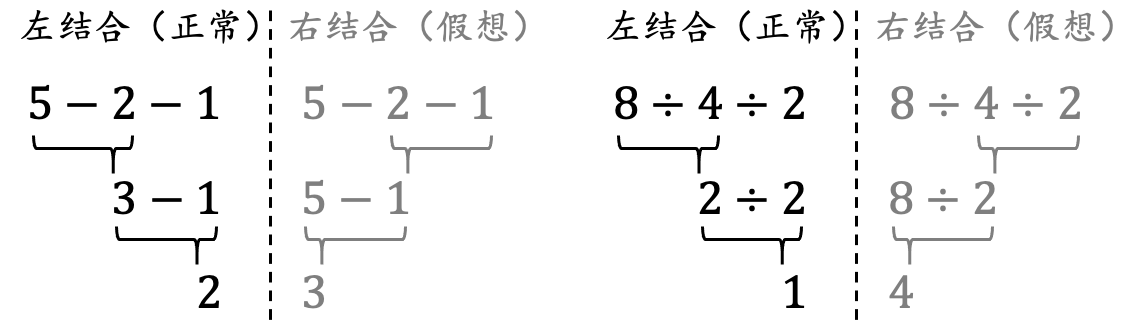
在计算减法算式和除法算式时，就要特别小心结合性的问题，请看如下示例：

示例： 举例说明结合性对加减乘除四则运算的影响。

解： 结合性对减法和除法运算是至关重要的，如图 5 所示。

结合性对运算的影响
结合性对加法（乘法）运算的影响并不大，有多个相邻的加法（乘法）运算符时，先计算哪个都行。这被称为加法（乘法）结合律，我们将在下一节讨论该定律。

☐


括号用来改变运算的优先级，先计算括号内的表达式。

♣ 请注意，有时出于计算的方便，我们常常需要改变运算次序。在涉及到减法和除法时，你要小心从事，请看如下示例：

示例： 在级联的减法和除法算式中使用括号要格外小心。示例如图 6 所示。

括号对算式的影响

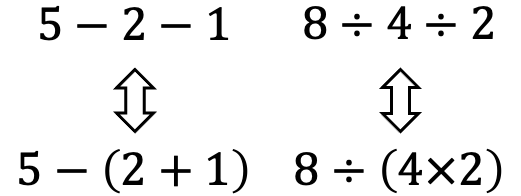
示例： 尝试去掉给出的算式中的括号，不改变计算结果：

示例： 尝试以 \(8\times(4\times2)\) 为种子，按照前述示例写出对应的四个算式（将乘号改为除号）

示例： 有时通过加减括号改变结合次序，可以使计算变得简单。例如：

在实际计算中，你需要能够快速地发现凑成整十整百整千的部分，才能够灵活地运用这种计算技巧。

☐


思考与讨论

♣ 如果涉及到加法（减法）和乘法（除法）的混合运算。去掉或加上括号就不仅仅是改变某个符号那么简单了。我们将在 一节中继续讨论这个问题。

运算定律

在整个小学期间，我们一直学习算数，从十以内加减法到分数的混合运算。这些运算的核心是以下一些运算定律：1

运算定律（教材上明确给出的）

教材未列出的运算定律（ \(a,b\) 为自然数）

交换律和结合律

交换律和结合律使加法（乘法）可以自由地交换运算次序。我们可以说“若干个数的和（乘积），而无需强调运算次序。

示例： 通过改变运算次序，简便计算如下算式：

\(56+27+33+14 \qquad 125 \times 25 \times 4 \times 8\)

\(56-27-16+17 \qquad 540 \div 4 \div 5 \div 9\)

思考与讨论

分配律

分配律可以让人们在计算乘法的时候，将乘数凑成比较容易计算的形式。不但可以合并乘数凑整，也可以拆分乘数凑整。

示例： 利用乘法结合律，简便计算如下算式：

\(13\times17 + 13\times 3 \qquad 127\times8\)

\(24\times 6 + 25\times6 \qquad 125\times9\)

封闭性和单值性

对减法和除法追求封闭性的会扩展数域至有理数。对平方运算和多项式的学习会扩展数域至复数，同时会导致单值性的丧失。这超出了我们目前讨论的范围。

单调性

单调性在小学阶段的意义主要在于比较大小和估算，这里只说估算。小学课本上的乘法估算方法是将某一个乘数改为相邻近的整十甚至整百。这样能够简便算出大概的结果，并且使用单调性判断估算结果是大了还是小了

示例： 对下列乘法算式进行估算，并指出估算的结果和实际结果的差距。

\(39\times25 \qquad 41\times39 \qquad 49\times19\)

估算的一个重要应用是检验计算结果的正确性：

示例： 对下列乘法算式进行估算，并指出估算的结果和实际结果的差距。

\(39\times25 \qquad 41\times39 \qquad 49\times19\)

课内教材中运用单调性的另一处地方是分数比较大小，我们等讲到分数时再说。这里仅仅给出几个例子：

\(\dfrac{1}{6}>\dfrac{1}{7} \qquad \dfrac{2}{5}<\dfrac{3}{5} \qquad \dfrac{6}{8}<\dfrac{7}{9}\)

思考与讨论

单调性还保证了逆的存在，减法（除法）是加法（乘法）的逆运算。你能举出一个没有逆的运算么？

几何

基本概念

几何知识从一组基本概念的定义开始：

过两点能做“两条”的，都不是直线
直角和平角
直角、锐角和钝角

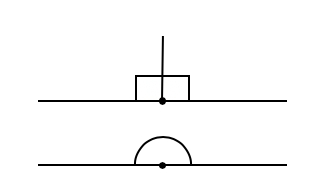
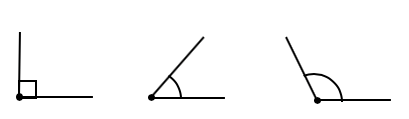
基本概念：点、线和角

圆、圆心、直径和半圆
圆心角被分为 \(360^\circ\)

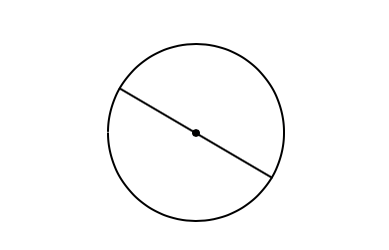
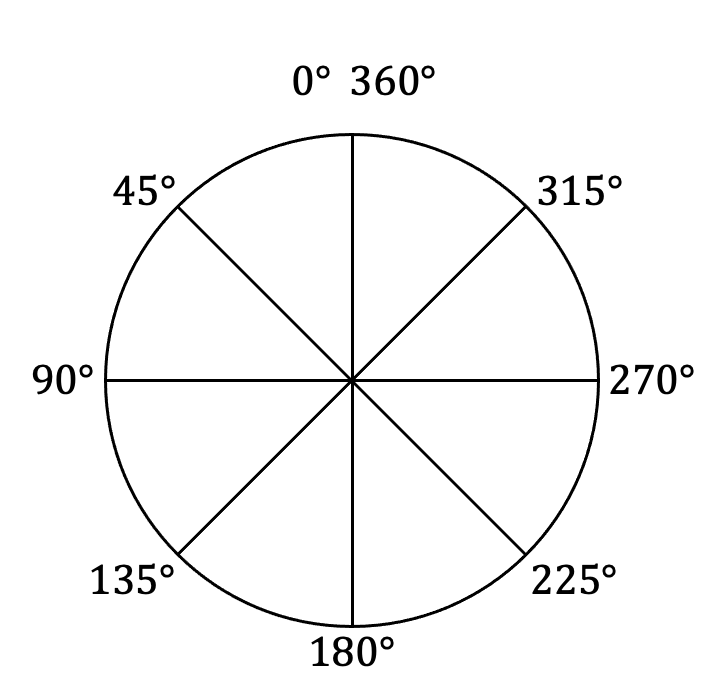
有了点、线、角的概念后，就可以引出各种几何图形了。比如圆、三角形和正方形等各种图形。古希腊人认为圆是最完美的图形，他们的几何学也从圆开始：

基本概念：圆

一般四边形、正方形和长方形

多边形的周长面积容易计算，所以小学生学习几何，往往从正方形的周长和面积开始：

基本概念：多边形

图形的运动

图形的缩放

将放大后的图形画出来

图形的翻转

按对称轴画出对称图形

图形的旋转

按旋转中心画出顺时针旋转 \(90^\circ\) 的图形

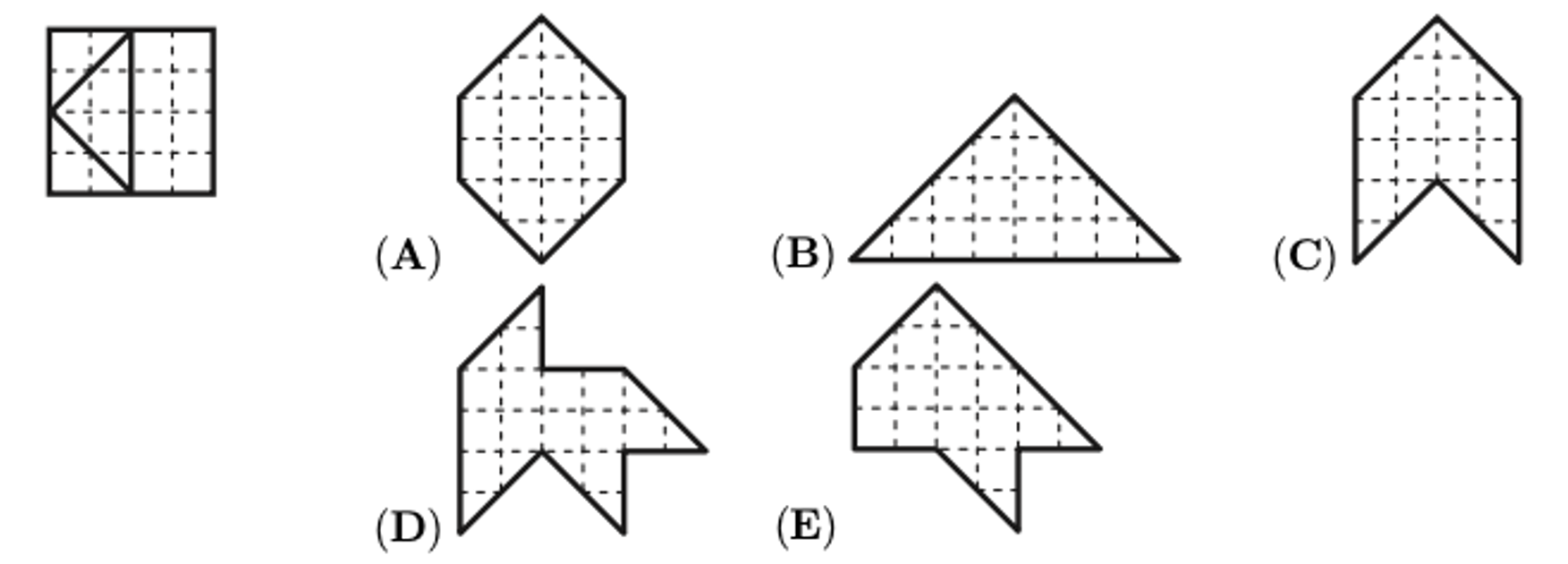
示例： (Math Kangaroo 2014 Level-1) 如图 16 所示，正方形被分为四部分。 ABCDE 所示图形中哪一个能够由这四部分拼出？

拼图-I

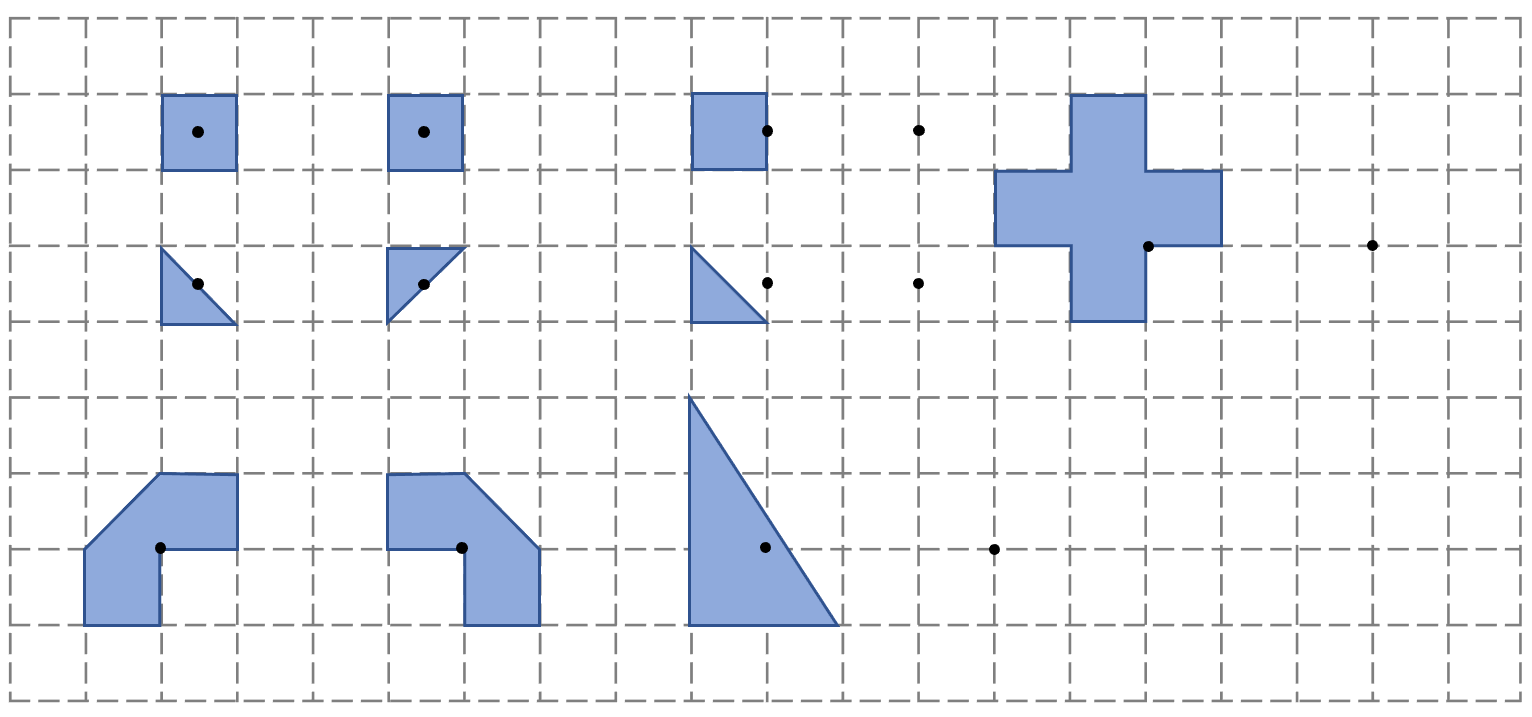
示例： (Math Kangaroo 2014 Level-2) 下列图形中，哪几个是由完全相同数目和大小的基本形状拼成？

拼图-II

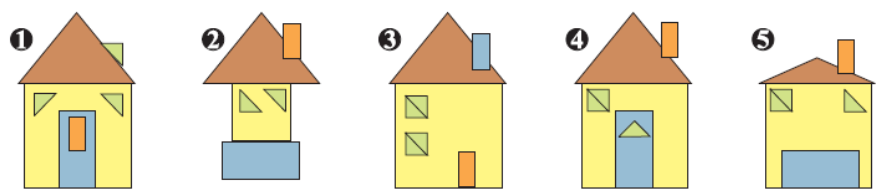
示例： (Math Kangaroo 2014 Level-2) 在先放入一块 T 型图片的情况下， 图 18 所示的 ABCDE 哪个图形能用剩下三块拼图拼出？

拼图-III

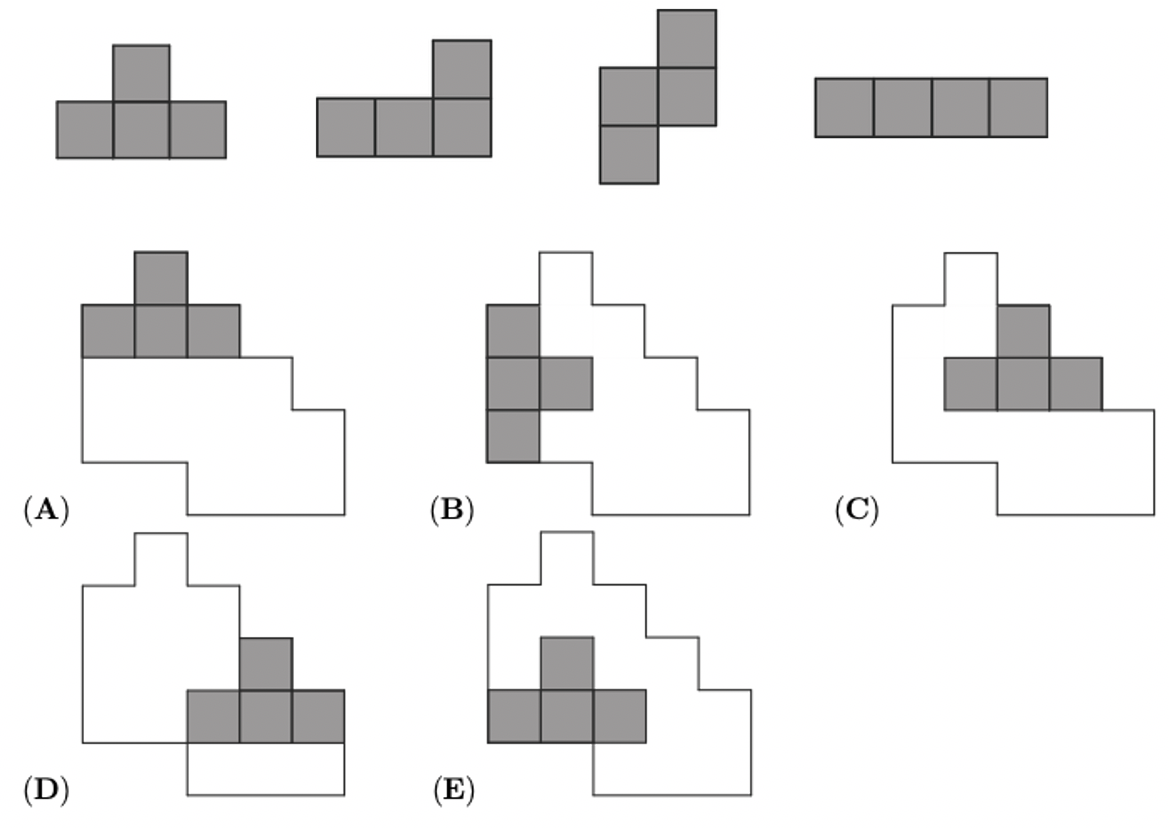
示例： (Math Kangaroo 2014 Level-2) 将 ABCDE 哪一个填入问号位置，可以使得深色和浅色部分的面积相同？

拼图的面积-IV

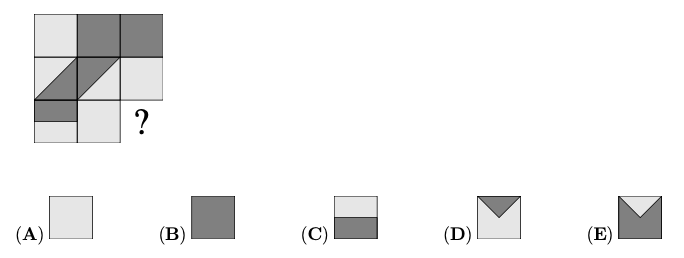
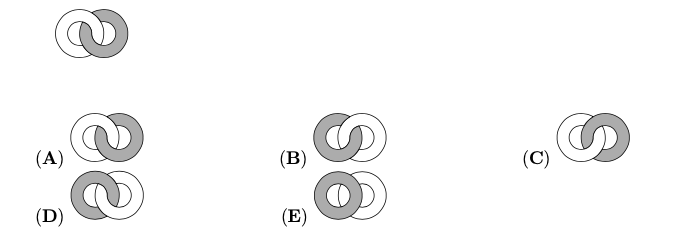
示例： (Math Kangaroo 2014 Level-3-02) 两个环，一个灰色、一个白色，被套在一起。 Peter 从这两个环的前面看到如图的景面。 Paul在这两个环的后面。他看到什么?

翻转圆环

几何计算的基本定律

虽然到目前为止我们只学过一些定义，但已经可以做很多事情了。但在继续之前，要梳理一下我们赖以生存几条重要定律：

几何的定律

第一条定律说明了我们的空间不是什么“魔法空间”。一个几何图形转一圈回来，还应该是原来的几何图形。第二条是我们在算术计算中早已经熟悉的定律。第三条定律让我们可以在图形进行一系列变换的同时保持某种性质不变（主要是面积）。

下面我们通过几个例子来看一下如何利用我们仅有的知识（长方形面积等于长乘以宽）来解决各种复杂问题。

示例： 求图 21 中三角形的面积

按对称轴画出对称图形

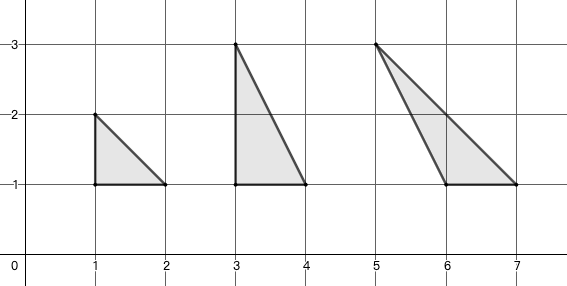
示例： 求图 22 所示图形的面积

按对称轴画出对称图形

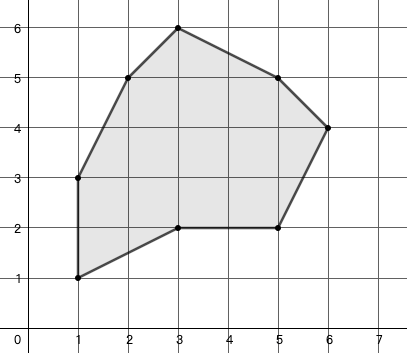
随堂练习 0

练习： 如果 \(m=2\) 并且 \(n=16\) ，求下列各个表达式的值：

\(m+10 \quad\qquad n+8 \quad\qquad 9-m \quad\qquad 22-n\)

\(n\div4 \quad\qquad 12\div m \quad\qquad n\cdot 13 \quad\qquad 6\cdot m\)

\(m+n \quad\qquad n+m \quad\qquad n-6 \quad\qquad m-1\)

练习： 某个品种的竹子在特定时期的长高速度满足表达式 \(rt\) ，其中 \(r\) 表示增长的速度， \(t\) 表示时间。如果增长速度 \(r\) 是每天 \(3\) 厘米，根据表达式计算 \(7\) 天竹子长了多高？

练习： 矩形的周长公式是 \(2\cdot(l+w)\) ，其中 \(l\) 代表矩形的长 (length) ， \(w\) 代表矩形的宽 (width) 。求图 23 所示矩形的周长。

矩形

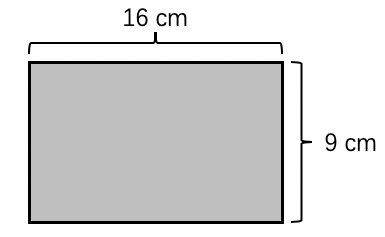
练习： 矩形的面积公式是 \(l\cdot w\) ，其中 \(l\) 代表矩形的长 (length) ， \(w\) 代表矩形的宽 (width) 。求图 23 所示矩形的面积。

练习： 找出下列表格的函数关系：

练习： ABCD 四个选项的表达式，哪一个能够恰当表示表格中 y 和 x 的关系？

A. \(2x+3\) \(\qquad\) B. \(x+3\) \(\qquad\) C. \(3x-2\) \(\qquad\) D. \(6-x\)

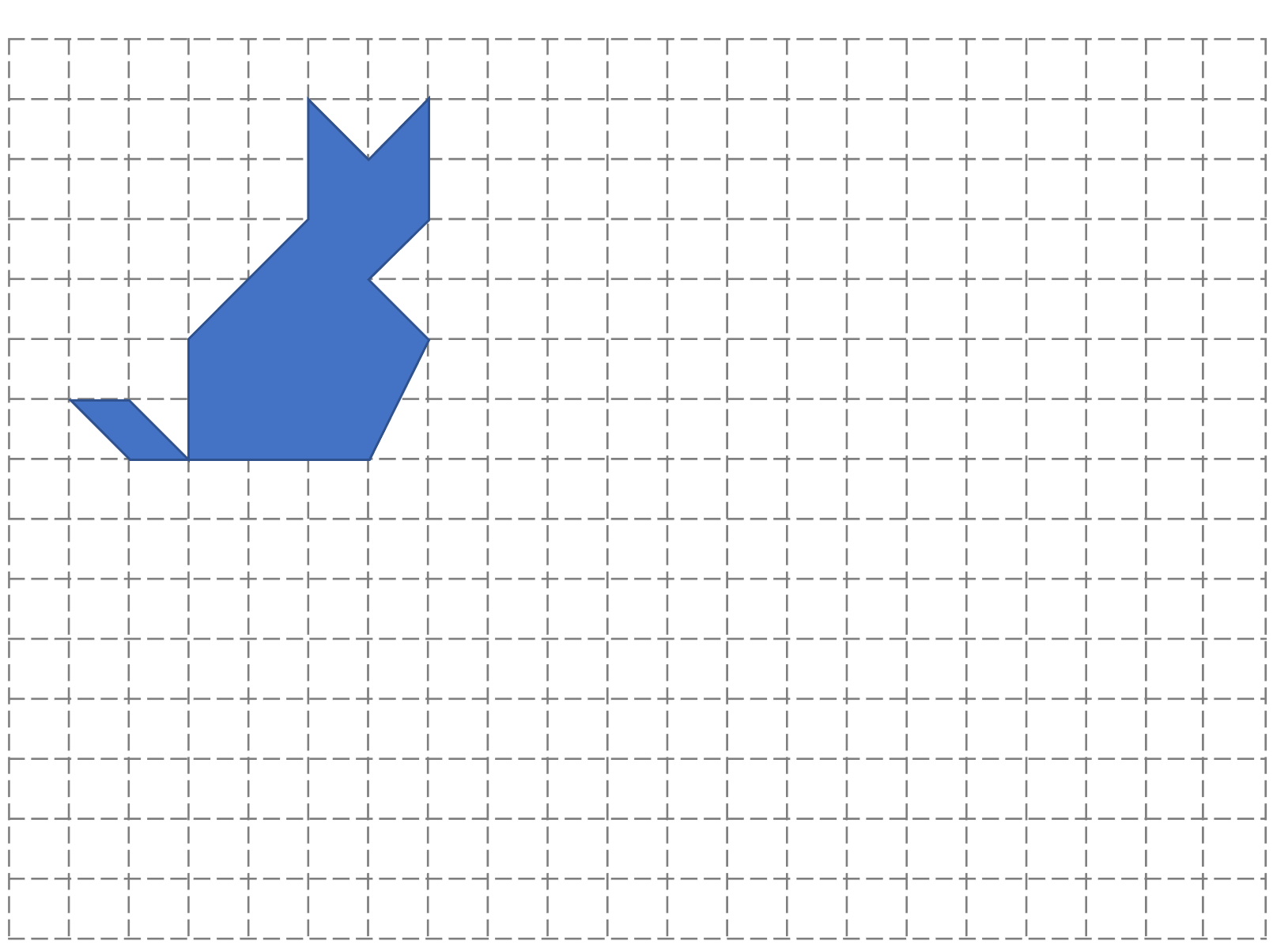
练习： 将下面的这个图形，长度和宽度各放大一倍画出来

将放大后的图形画出来

练习： (AMC 8 1999-05) 汤姆家的羊圈的是用篱笆围起来的。篱笆墙围成的长方形原本有 \(50m\) 长 \(10m\) 宽。如果汤姆用原来的篱笆把形状改成正方形，那么羊圈的面积会增大多少？

汤姆家的篱笆围墙

练习： (AMC 8 2000-06) 如图 28 所示， ABCD 是正方形，在图形的左上、中间和右下的三块也是正方形。问阴影部分面积是多少？

求 L 型阴影的面积

练习： (AMC 8 2000-18) 在图 29 中，有两块图形 I 和 II。以下四个说法，哪一个是对的

面积和周长

练习： (AMC 8 2002-15) 图 30 所示多边形中，哪一个面积最大？

多边形

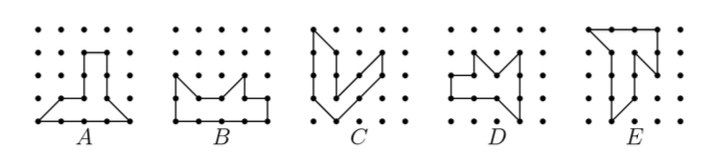
练习： (Math Kangaroo 0506 2017-16) 现代家具店的家具都是模块化拼装的。用同样的基本形状拼成不同的家具。图 31 展示了家具店出售的三人沙发、双人沙发和单人沙发的平面俯视图（从上面看下去的样子）。三人沙发宽 \(220cm\) ，双人沙发宽 \(160cm\) 。请问单人沙发的宽度是多少？

家具平面图

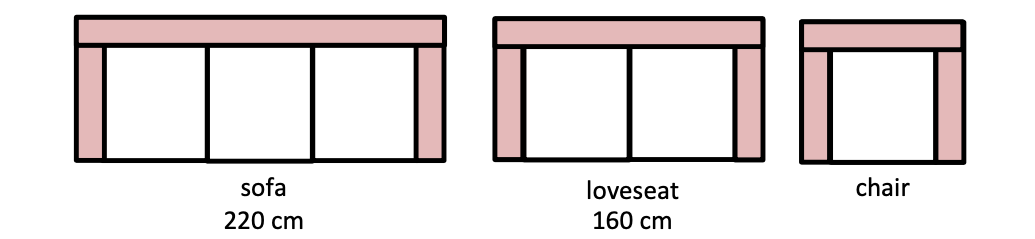
练习： (Math Kangaroo 0506 2017-02) Alice 有 \(4\) 块 \(1\times3\) 的方格纸，她不能拼出下面哪一个图形？

拼图

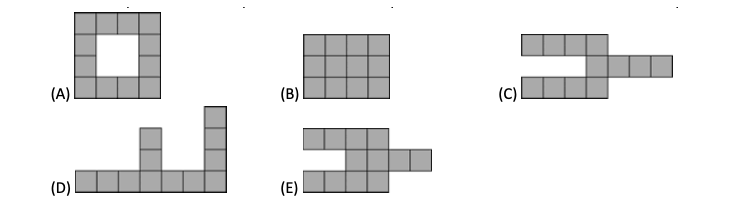
练习： (Math Kangaroo 0506 2017-05) Martin 宝宝在练习涂色，他把图 33 中 \(1/3\) 的格子涂成蓝色， \(1/2\) 的格子涂成黄色，剩下的格子涂成红色。请问 Martin 涂了多少个红色格子？

格子涂色

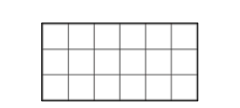
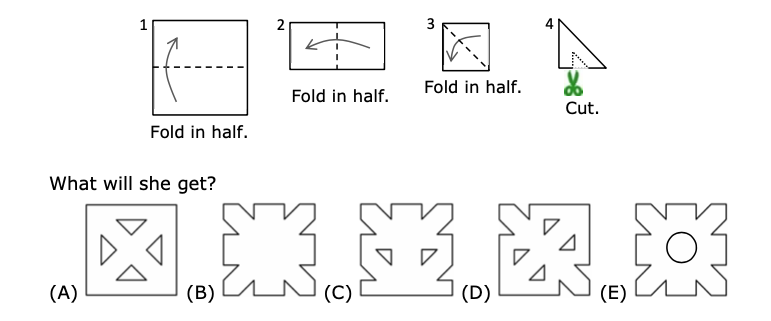
练习： (Math Kangaroo 0506 2017-10) 将正方形的纸折起来，扎一个洞再打开，纸上会出现图 34 所示的四个洞。请问纸的折痕可能是 ABCDE 中的哪个？

折纸的洞

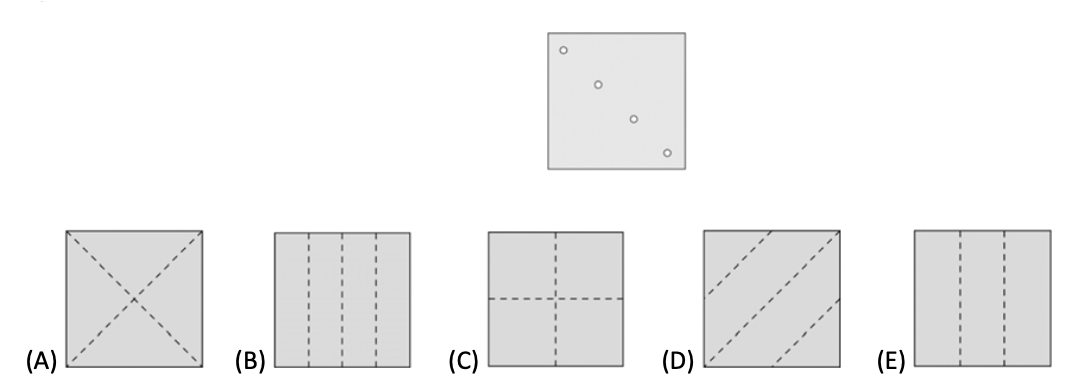
练习： (Math Kangaroo 0506 2017-26) 在图 35 中，虚线两侧的袋鼠是轴对称的。如果空白的三角形都画满袋鼠，那么阴影处的三角形的袋鼠是 ABCDE 中的哪一个样式？

对称的袋鼠

习题 0A

问题： 如果 \(a=4\) ， \(b=7\) 并且 \(c=11\)，求下列表达式的值：

\(2b-a\) \(\qquad\) \(2c-3b\) \(\qquad\) \(5c+6\)

\(2b+7\) \(\qquad\) \(3a-4\) \(\qquad\) \(4b-10\)

问题： 跳棋 \(15\) 元一副，一单运费 \(5\) 元。一单买 \(n\) 副跳棋的花费是 \(15n+5\) 元。使用该表达式计算购买 \(7\) 副跳棋的花费。

问题： 正方形的边长为 \(s\) ，写出计算正方形周长的表达式。

问题： (Math Kangaroo 0506 2016-01) 图 36 中哪个图形有最多的对称轴？

数对称轴

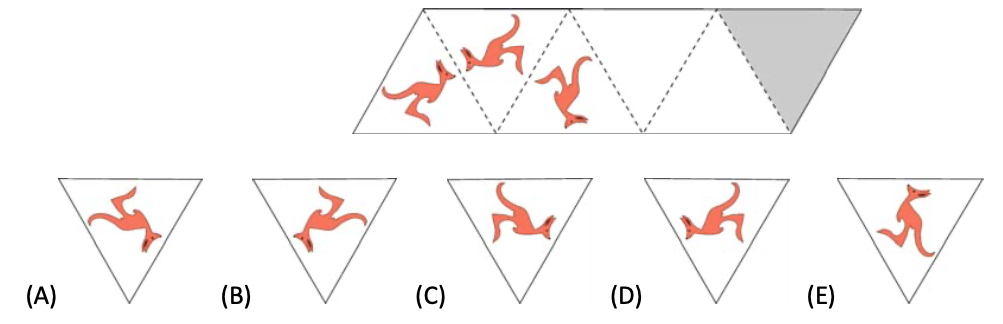
问题： (Math Kangaroo 0506 2016-13) Bart 正在理发，他从镜子中看到的时钟如图 37 所示。请问十分钟前镜子中的时钟是什么样子？

镜子中的钟

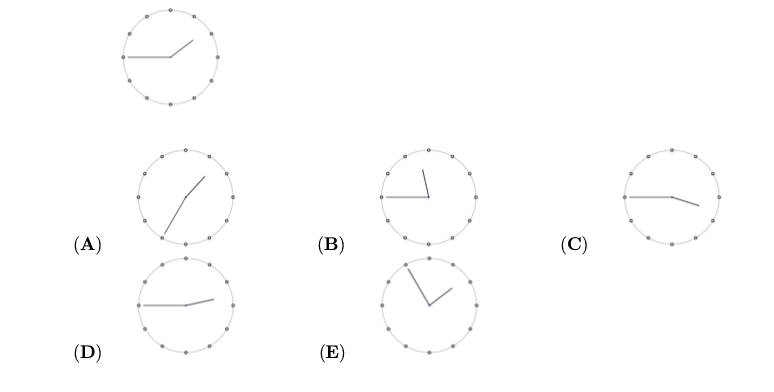
问题： (Math Kangaroo 0102 2017-17) 如图 38 所示，将正方形纸片折叠后剪去一个小三角形，展开后的图样是什么？

窗花剪纸

问题： (Math Kangaroo 0102 2017-17) 如图 39 所示，从图示右侧的缺两个正方形洞的纸片上剪下图示左侧的凸型纸片，有多少种不同的剪法？

凸型纸片

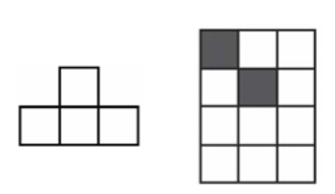
问题： (Math Kangaroo 0102 2018-01) 如图 40 所示，ABCDE 五个图案哪个不能用给出的 T 型和十字型纸片拼出？

拼图

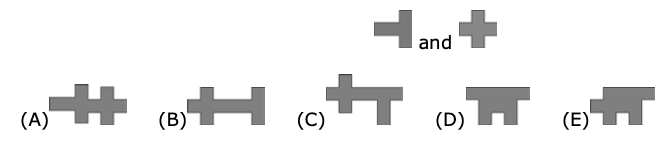
问题： (Math Kangaroo 0506 2016-04) 连接图 41 中大正方形边上中点，得到一个小正方形。请问小正方形的面积是多少？

正方形面积

习题 0B

问题： 如果 \(a=4\) ， \(b=15\) 并且 \(c=9\)，求下列表达式的值：

\(c^2+a\) \(\qquad\) \(b^2-5c\) \(\qquad\) \(3a\div4\) \(\qquad\) \(4b\div5\)

\(5b\div2\) \(\qquad\) \(5b-2ac\) \(\qquad\) \(2ac\) \(\qquad\) \(3ab\div c\)

问题： 我们使用表达式 \(d\div t\) 计算赛车的平均速度。其中 \(d\) 表示距离， \(t\) 表示赛车跑过这段距离所用的时间。一辆赛车在 \(4\) 小时跑过了 \(508\) 公里，赛车的平均速度是多少？

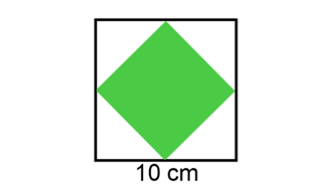
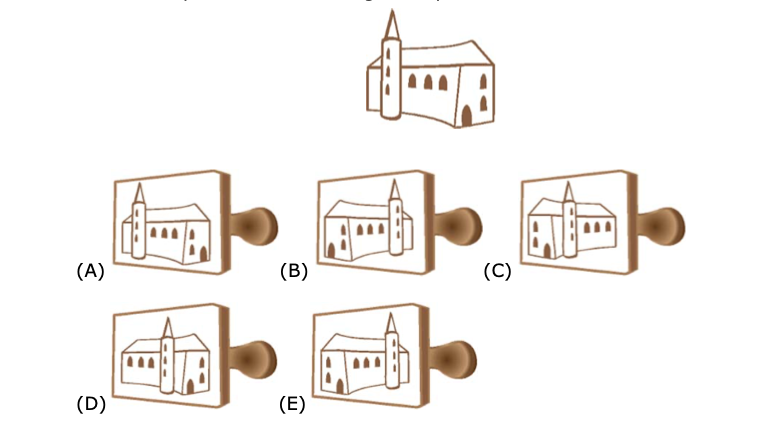
问题： (Math Kangaroo 0102 2017-17) 如图 42 所示，哪一个印章能够盖出图中所示的图案？

印章

问题： (Math Kangaroo 0102 2018-05) 图 43 中有几只右手？

手

问题： (Math Kangaroo 0506 2016-18) 如图 44 所示， Anna 把一张圆纸对折。之后她把纸对折多一次，然后再对折最后一次。最后 Anna 把她折后的纸沿着虚线剪开。这张纸打开后的形状是怎样的？

剪窗花

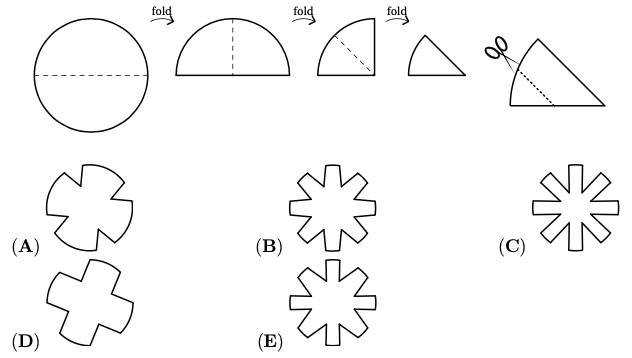
问题： (Math Kangaroo 0102 2016-15) 图 45 中 ABCDE 哪个图形不能被“凸”型图案拼出来？

打孔纸带

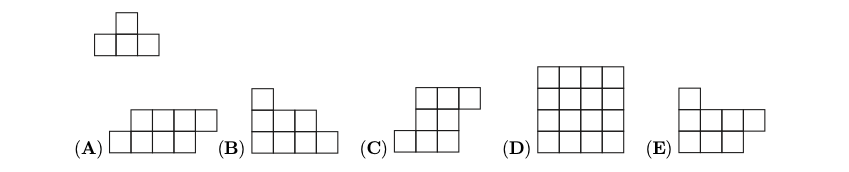
问题： (Math Kangaroo 0506 2016-08) 使用两个一样的正方形，无法拼出图 46 中 ABCDE 所示的哪个图形？

合二为一

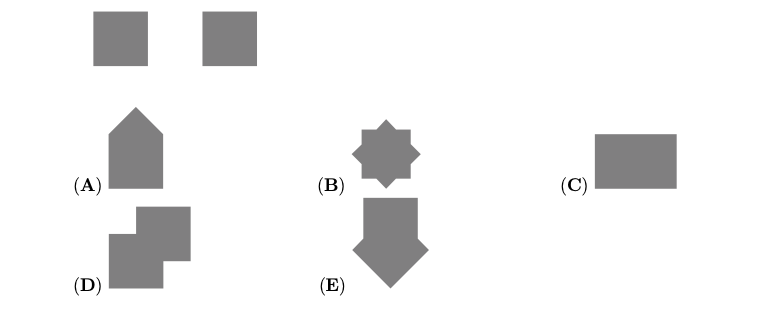
问题： (Math Kangaroo 0506 2016-17) 长方形 ABCD 的周长是 \(30cm\) 。有另三个长方形的中心为点 A, B 和 D （如图 47 所示）。这三个 长方形(其中心分别为点 A, B 和 D 者)的周长之和是 \(20cm\) 。请问粗线的总长度是多少？

周长和面积

习题 0C

问题： (Math Kangaroo 0102 2018-16) 图 48 中的一根小木条长 \(5cm\) 宽 \(1cm\) ，请问用它拼出来的图案有多长？

木条图案

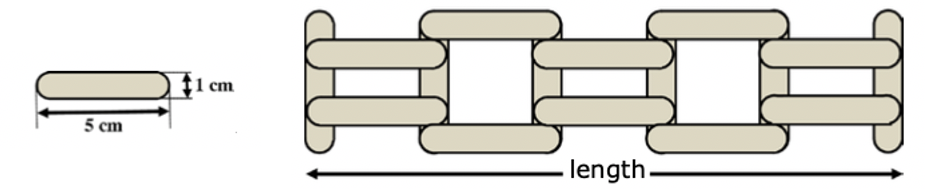
问题： (Math Kangaroo 0304 2018-11) 为了拼出图 49 所示的船，需要几个图示的正方形和梯形？

船

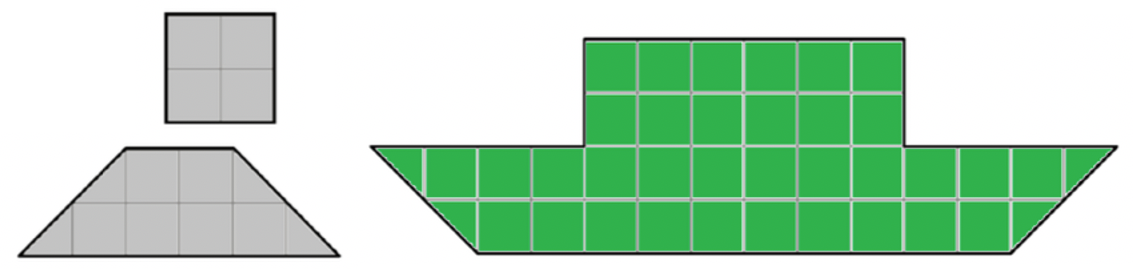
问题： (Math Kangaroo 0304 2016-12) 图 50 中 哪三片可以拼出正方形？

拼出正方形

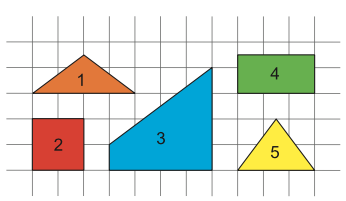
问题： (Math Kangaroo 0304 2018-18) 图 51 中显示的带有五种固定方法。举例来说，下图显示使用一个洞固定的带。请问，使用 一个洞固定的带会比使用五个洞固定的带长多少?

打孔纸带

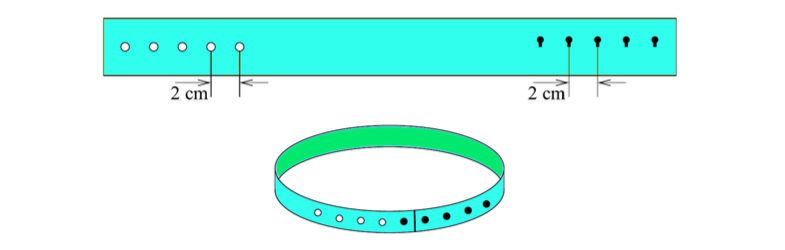
问题： (Math Kangaroo 0506 2015-10) 图 52 中的图案由边长为 \(1\) 的正方形组成，请问整个图案的边长是多少？

正方形组成的图案

问题： (Math Kangaroo 0506 2016-22) 如图 53 所示， 一个大立方体是由八个相同大小的小立方体建成的，一些立方体是黑色的，一些是白色的。大立方体的其中五面如下。请问第六面是怎样的？

黑白立方体

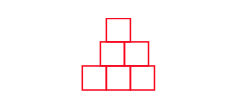
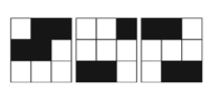
问题： (Math Kangaroo 0304 2015-16) 有三张印着黑色格子的透明薄片（如图 54 所示）。只可以旋转但不能翻动，将他们重合在一起从正面看，最多可以看见几个黑色格子？

黑白立方体

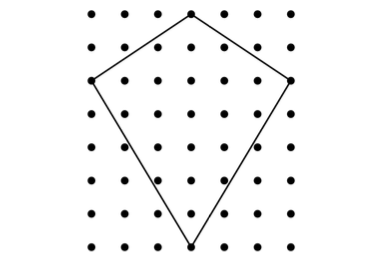
问题： (AMC 8 2001-789) 笑笑要做一个风筝，她按照图 55 所示图样来做。图样的格点间距为 \(1cm\) ，笑笑把水平方向和垂直方向都放大为原来的 \(5\) 倍。请回答如下问题：

面积和周长

习题 0D：数量关系的计算

问题： 三个桃子和五个李子重 \(1350\) 克，一个桃子和一个李子重 \(410\) 克。请问桃子和李子各重多少克？（假定桃子重量都一样，李子重量也都一样）

课上讲过

问题： 五个桃子和六个李子重 \(2220\) 克，四个桃子和三个李子重 \(1650\) 克。请问桃子和李子各重多少克？（假定桃子重量都一样，李子重量也都一样）

课上讲过

问题： 两个桃子和三个李子重 \(840\) 克，三个桃子和两个李子重 \(1110\) 克。请问桃子和李子各重多少克？（假定桃子重量都一样，李子重量也都一样）

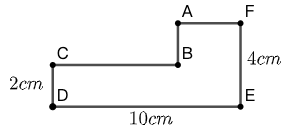
问题： 如图 56 所示，多边形 ABCDEF 面积为 \(26cm^2\) ，其相邻边都互相垂直，尺寸标注如图。求图中未标注长度的线段 \(AB\) ， \(BC\) 和 \(AF\) 的长度。

L型多边形

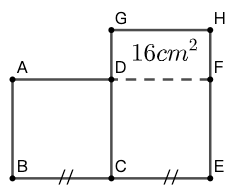
问题：=16cm^2$ 。求矩形 \(ABCD\) 和 \(CEHG\) 的面积。

L型多边形

问题： 鸡和兔子共 \(10\) 只，腿 \(26\) 条。请问鸡和兔子各多少只？

问题： 淘气有红色弹球和蓝色弹球共 \(80\) 个。红色弹球比蓝色弹球多 \(16\) 个。请问红色弹球和蓝色弹球各多少个？

问题： (冲刺 100 三下 Page - 48 解决问题-7) 哥哥有 \(96\) 枚邮票，弟弟有 \(60\) 枚邮票，哥哥给弟弟多少枚邮票后，弟弟的邮票是哥哥的 \(2\) 倍？

从此题往后，取自练习册《期末冲刺 100 三年级下》 - 长春出版社

问题： (冲刺 100 三下 Page - 72 解决问题-4) 淘气家里有五盒茶叶，如果从每盒茶叶中取出 \(300\) 克， \(5\) 盒中剩下的茶叶正好与原来两盒茶叶的质量相等。请问原来每盒茶叶有多少克？

问题： (冲刺 100 三下 Page - 76 解决问题-4) 参加体操表演的同学站成若干排若干列的方阵。小伟站在第 \(8\) 排左起第 \(7\) 列，倒数第 \(13\) 排右起第 \(19\) 列。请问参加体操表演的同学共有多少人？

问题： (冲刺 100 三下 Page - 76 附加题) \(10\) 张边长为 \(2\) 厘米的正方形纸片叠放成如图 58 所示的图形，重叠部分的边长为原来每个正方形边长的一半。问这个图形的周长是多少？

叠放的正方形

问题： (改编自 冲刺 100 三下 Page - 80 解决问题-2) \(\bigstar\bigstar\) 李叔叔计划用 \(28\) 米的篱笆一面靠墙未出一块长方形菜地，如图 59 所示。

篱笆和菜地

问题： (冲刺 100 三下 Page - 80 解决问题-4) 暑假学校组织 \(58\) 名老师去旅游，租车费用如下：

请你设计几种租车方案，并算出怎样租车最省钱。

问题： (冲刺 100 三下 Page - 80 附加题) 一个大瓶子倒进 \(4\) 碗水，连瓶共重 \(1000\) 克；倒进 \(6\) 碗水，连瓶共重 \(1400\) 克。问瓶子重多少克？

问题： (冲刺 100 三下 Page - 84 走进生活-3) 贝贝、丽丽、甜甜、乐乐四个人进行了 \(60\) 米短跑测试，成绩分别是： \(6\) 秒、 \(9\) 秒、 \(8\) 秒、 \(7\) 秒。

请你说说她们四个人的成绩各是多少？

问题： (冲刺 100 三下 Page - 84 附加题) 甲、乙两筐苹果共有 \(115\) 千克，如果从甲筐中取出 \(15\) 千克放入乙筐后，甲筐比乙筐的 \(2\) 倍还多 \(1\) 千克。问：甲、乙两筐原来各有多少千克苹果？

习题 0E：三年级计算练习

去掉下列算式的括号，保持运算结果不变，并计算结果。（选择有无括号时比较容易计算的算式计算）

\(10-(2+3)\) \(\qquad\) \(1+(2-3)\) \(\qquad\) \(25-(20-5-6)\)

\(16\div(2\times4)\) \(\qquad\) \(36\div(12\div2\div3)\) \(\qquad\) \(36\div(9\times4)\)

去掉下列算式的括号，保持运算结果不变，并计算结果。

\((11+10)-(9+8)+(7+6)-(5+4)+(3+2)\)

改变运算次序，简化运算，并计算结果。

\(450\div5\div2\) \(\qquad\) \(125+84+16\) \(\qquad\) \(1200\div25\div4\)

\(457-(100-63)\) \(\qquad\) \(525+184-84\) \(\qquad\) \(1200\div25\div4\)

将两位数拆开（\(12=10+2\)），用分配律计算下列算式：

\(12\times6\) \(\qquad\) \(13\times7\) \(\qquad\) \(14\times8\)

\(15\times9\) \(\qquad\) \(16\times8\) \(\qquad\) \(17\times7\)

将两位数拆开（\(22=20+2\)），用分配律计算下列算式：

\(22\times6\) \(\qquad\) \(33\times7\) \(\qquad\) \(44\times8\)

\(55\times9\) \(\qquad\) \(66\times8\) \(\qquad\) \(77\times7\)

用分配律计算下列算式，并用计算器验证。

提示：\(12\times(10+2)=12\times10+12\times2\)

\(11\times11\) \(\qquad\) \(12\times12\) \(\qquad\) \(13\times13\) \(\qquad\) \(14\times14\) \(\qquad\) \(15\times15\)

\(16\times16\) \(\qquad\) \(17\times17\) \(\qquad\) \(18\times18\) \(\qquad\) \(19\times19\)

用分配律计算下列算式，并用计算器验证。

\(21\times21\) \(\qquad\) \(22\times22\) \(\qquad\) \(23\times23\) \(\qquad\) \(24\times24\) \(\qquad\) \(25\times25\)

\(26\times26\) \(\qquad\) \(27\times27\) \(\qquad\) \(28\times28\) \(\qquad\) \(29\times29\)

计算下列算式，并用计算器验证。

\(51\times18\) \(\qquad\) \(75\times22\) \(\qquad\) \(21\times14\) \(\qquad\) \(26\times35\)

\(15\times73\) \(\qquad\) \(45\times80\) \(\qquad\) \(99\times16\) \(\qquad\) \(24\times47\)

习题 0F：四年级上学期期末复习（上）

问题： 一个数各数位上的数字之和是 \(80\) ，这个数最小是多少？

问题： 用 0,3,4,6,9 五张数字卡片（每个数字就一张卡片）摆出所有大于 \(36000\) 且小于 \(39000\) 的数，并把这些数字按从小到大的顺序排列起来。

问题： 六位数 \(AB3456\) 与六位数 \(BA3456\) 相差 \(180000\) 。六位数 \(AB3456\) 可能是多少？请写出所有答案。

问题： 一个数，各数位上的数字之和是 \(33\) ，且各数位上的数字互不相同，这个自然数最大是多少？最小是多少？

问题： 有五张数字卡片 9,5,4,1,0 ，用这五张数字卡片组成一个五位数，且把这个五位数精确到万位的近似数是 \(10\) 万，这个五位数最小是多少？

问题： 有一类七位数，中间断开可以分成一个三位数和一个四位数，但无乱拆分成前三位、后四位，还是前四位、后三位，每次拆分的两个数但和总是相等的，这类七位数中最小的数是多少？最小的数接近多少万？

问题： 一个两位数，个位上的数字比十位上的数字小 \(1\) ，把个位上的数字和十位上的数字交换位置后得到一个新的两位数。原数与新数相加的和是 \(77\) ，求这个两位数。

问题： 五个连续自然数的和是 \(240\) ，这五个数中最大的数是多少？最小的数是多少？

问题： 小亮买了一本《海底世界》，这本书一共有 \(527\) 页。你知道编排这本书一个用了多少个数字吗？

问题： 下图中有多少条线段？

问题： \(2\) 条直线最多有 \(1\) 个交点， \(3\) 条直线最多有 \(3\) 个交点， \(10\) 条直线最多有几个交点？

问题： 一张纸上有三条直线，分别是直线 \(a,b,c\) ，已知 \(a\parallel b,b\parallel c\) ，并且直线 \(a\) 与 \(b\) 之间的距离是 \(7\) 厘米，直线 \(b\) 与 \(c\) 之间的距离是 \(4\) 厘米。请问直线 \(a\) 与直线 \(c\) 之间的距离是多少厘米？

问题： 三角形的 \(3\) 个内角合起来能组成一个平角，五边形的 \(5\) 个内角合起来能组成几个平角呢？六边形呢？

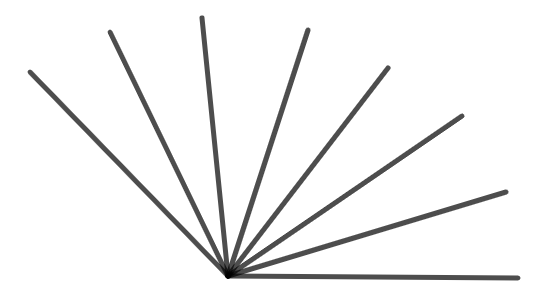
问题： 下图中共有多少个小于 \(180^\circ\) 的角。

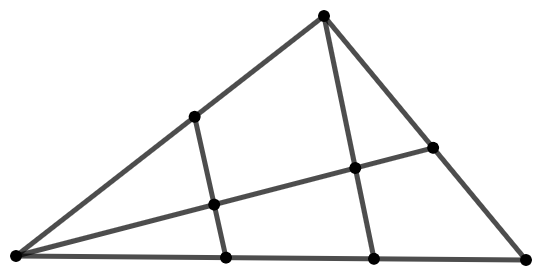
问题： 下图中共有多少条线段？

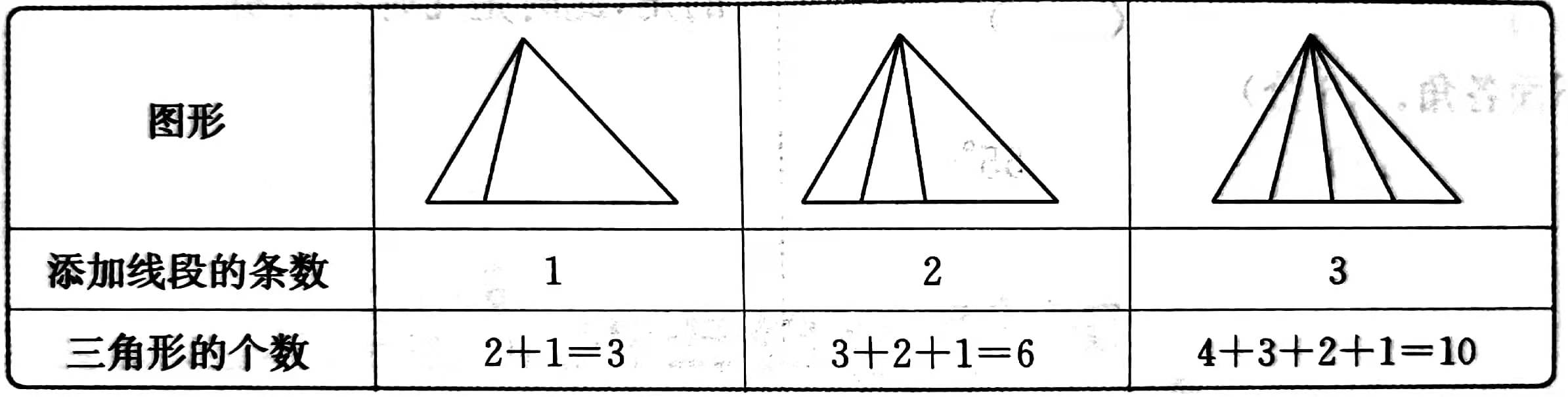
问题： 在三角形中添加不同数量的线段后，会得到不同数量的三角形，如下表所示。如此在三角形中添加 \(4\) 条、 \(5\) 条 …… \(10\) 条线段后，得到的图形中一共有多少个三角形？

问题： 数一数，下面每个图形中有多少条对角线？想一想，图形的顶点数与对角线的总条数之间有什么关系？

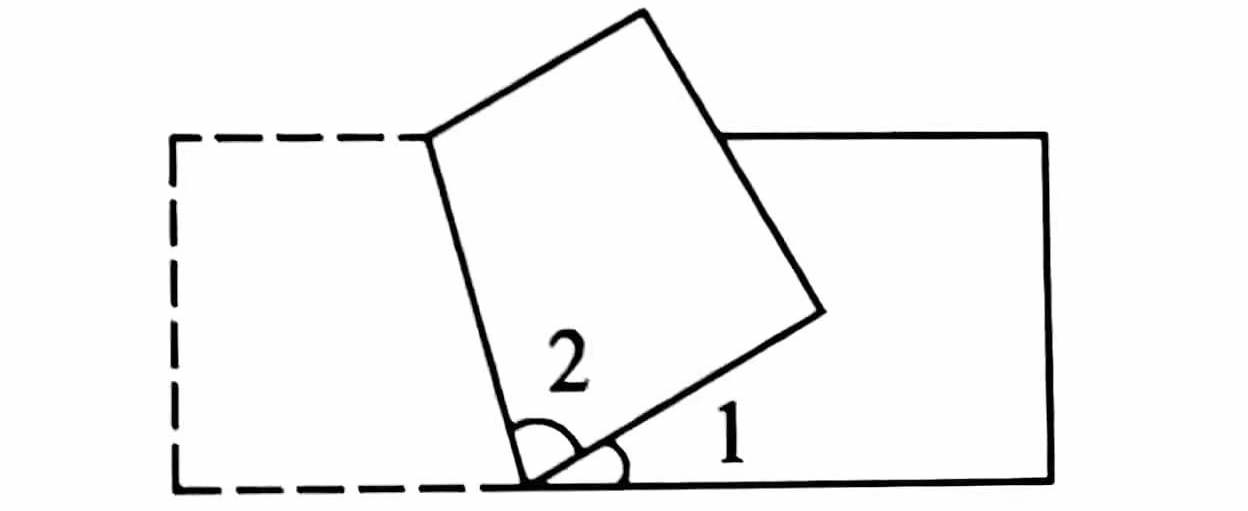
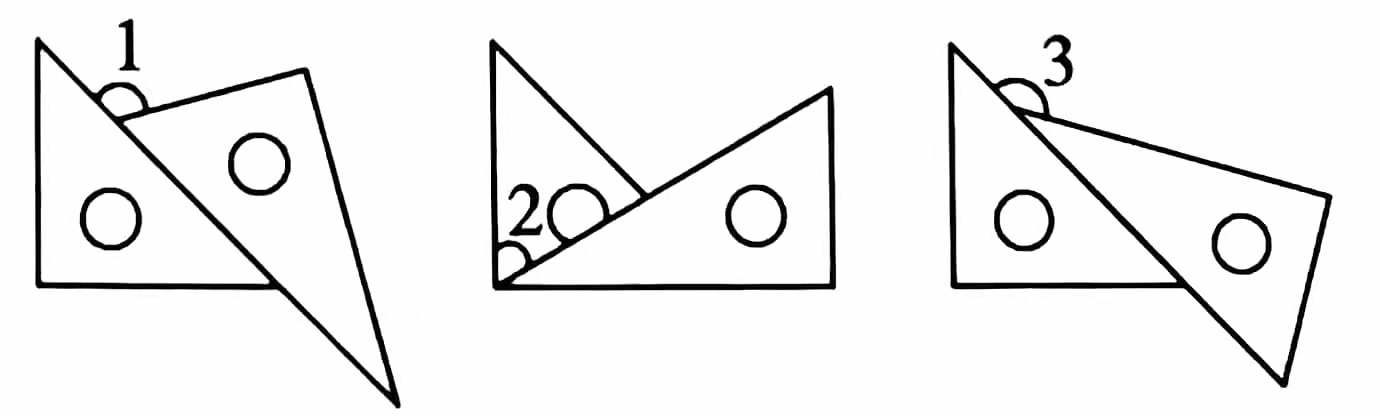
问题： 下图三幅图都是由一副三角尺拼成的，\(\angle{1}\) 、\(\angle{2}\) 和 \(\angle{3}\) 各是多少度？

问题： 把一张长方形纸折成下图这样，已知 \(\angle{1}=30^\circ\) ，求 \(\angle{2}\) 的度数。

参考文献

Klein, Felix, E. R. Hedrick, and C. A. Noble. 1954. Elementary Mathematics from an Advanced Standpoint, Vol. I, Arithmetic, Algebra, Analysis. unkown.

  1. (Klein, Hedrick, and Noble 1954)-page?↩︎