向量真题汇编

向量真题汇编

向量真题汇编（技巧分类）

向量的定义和代数运算

问题：1 已知向量 \(\boldsymbol{a},\boldsymbol{b}\) 满足 \(|\boldsymbol{a}|=1,|\boldsymbol{b}|=\sqrt{3},|\boldsymbol{a}-2\boldsymbol{b}|=3\) ，则 \(\boldsymbol{a}\cdot\boldsymbol{b}=\)

A. \(-2\) \(\qquad\) B. \(-1\) \(\qquad\) C. \(1\) \(\qquad\) D. \(2\)

问题：2 已知向量 \(\boldsymbol{a}=(2,1),\boldsymbol{b}=(-2,4)\) ，则 \(|\boldsymbol{a}-\boldsymbol{b}|=\)

A. \(2\) \(\qquad\) B. \(3\) \(\qquad\) C. \(4\) \(\qquad\) D. \(5\)

问题：3 设向量 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角的余弦值为 \(\dfrac{1}{3}\) ，且 \(|\boldsymbol{a}|=1,|\boldsymbol{b}|=3\) ，则 \((2\boldsymbol{a}+\boldsymbol{b})\cdot\boldsymbol{b}=\_\_\_\_\_\_\)

问题：4 已知向量 \(\boldsymbol{a}=(m,3),\boldsymbol{b}=(1,m+1)\) 。若 \(\boldsymbol{a}\perp\boldsymbol{b}\) ，则 \(m=\_\_\_\_\_\_\) 。

问题：5 若向量 a,b 满足 \(|a|=3,\ |a-b|=5,\ a\cdot b=1\) ，则 \(|b|=\_\_\_\_\_\_\) 。

问题：6 已知向量 \(\vec{a}=(3,1),\vec{b}=(1,0),\vec{c}=\vec{a}+k\vec{b}\) ，若 \(\vec{a}\perp\vec{c}\) ，则 \(k=\_\_\_\_\_\_\)

问题：7 已知向量 \(\vec{a}=(2,5)\)，\(\vec{b}=(\lambda,4)\) ，若 \(\vec{a}\parallel\vec{b}\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：8 已知向量 \(\vec{a}=(1,3)\)，\(\vec{b}=(3,4)\) ，若 \((\vec{a}-\lambda\vec{b})\perp\vec{b}\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：9 已知向量 \(\vec{a}=(1,3)\)，\(\vec{b}=(3,4)\) ，若 \((\vec{a}-\lambda\vec{b})\perp\vec{b}\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：10 已知向量 \(\vec{a}=(1,3)\)，\(\vec{b}=(3,4)\) ，若 \((\vec{a}-\lambda\vec{b})\perp\vec{b}\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：11 在 \(\triangle{ABC}\) 中，\(D\) 是 \(AB\) 边上的中点，则 \(\overrightarrow{CB}=\)

A. \(2\overrightarrow{CD}+\overrightarrow{CA}\) $ \(\qquad\) $ B. \(\overrightarrow{CD}-\overrightarrow{2CA}\) $ \(\qquad\) $ C. \(2\overrightarrow{CD}-\overrightarrow{CA}\) \(\qquad\) D. \(\overrightarrow{CD}+2\overrightarrow{CA}\)

问题：12 设向量 \(\boldsymbol{a}=(1,-1), \boldsymbol{b}=(m+1,2m-4)\) ，若 \(\boldsymbol{a}\perp\boldsymbol{b}\) ，则 \(m=\_\_\_\_\_\_\)

问题：13 已知直线方程 \(2x-y+c=0\) 的一个方向向量 \(\overrightarrow{d}\) 可以是

A. \((2,-1)\) \(\qquad\) B. \((2,1)\) \(\qquad\) C. \((-1,2)\) \(\qquad\) D. \((1,2)\)

问题：14 已知向量 \(\boldsymbol{a}=(2,2),\boldsymbol{b}=(-8,6)\) ，则 $,=

问题：15 已知向量 \(\boldsymbol{a}=(-4,3)\) ， \(\boldsymbol{b}=(6,m)\) ，且 \(\boldsymbol{a} \perp \boldsymbol{b}\) ， 则 \(m=\_\_\_\_\_\_\_\_\)

问题：16 已知向量 \(\boldsymbol a, \boldsymbol b\) 满足 \(\left|\boldsymbol a\right|=1\) ， \(\boldsymbol a \cdot \boldsymbol b=-1\) ，则 \(\boldsymbol a \cdot (2\boldsymbol a-\boldsymbol b)=\)

  1. 4 \(\qquad\) (B) 3 \(\qquad\) (C) 2 \(\qquad\) (D) 0

问题：17 已知向量 \(\boldsymbol{a}=(1,2)\) ， \(\boldsymbol{b}=(2,-2)\) ， \(\boldsymbol{c}=(1,\lambda)\) 。若 \(\boldsymbol{c}\parallel(2\boldsymbol{a}+\boldsymbol{b})\) ， 则\(\lambda=\_\_\_\_\_\_\_\)

问题：18 设向量 \(\boldsymbol{a}=(1,0)\) ， \(\boldsymbol{b}=(-1,m)\) ，且 \(\boldsymbol{a} \perp (m\boldsymbol{a}-\boldsymbol{b})\) ， 则 \(m=\_\_\_\_\_\_\_\_\) 。

向量的几何意义

问题：19 在 \(\triangle{ABC}\) 中，点 \(D\) 在边 \(AB\) 上， \(BD=2DA\) ，记 \(\overrightarrow{CA}=\boldsymbol{m}, \overrightarrow{CD}=\boldsymbol{n}\) ，则 \(\overrightarrow{CB}=\_\_\_\_\_\_\)

A. \(3\boldsymbol{m}-2\boldsymbol{n}\) \(\qquad\) B. \(-2\boldsymbol{m}+3\boldsymbol{n}\) \(\qquad\) C. \(3\boldsymbol{m}+2\boldsymbol{n}\) \(\qquad\) D. \(2\boldsymbol{m}+3\boldsymbol{n}\)

问题：20 已知向量 \(\boldsymbol{a}=(3,4)\)，\(\boldsymbol{b}=(1,0)\) ， \(\boldsymbol{c}=\boldsymbol{a}+t\boldsymbol{b}\) ， 若 \(\langle\boldsymbol{a},\boldsymbol{c}\rangle=\langle\boldsymbol{b},\boldsymbol{c}\rangle\) ，则实数 \(t=\)

A. \(-6\) \(\qquad\) B. \(-5\) \(\qquad\) C. \(5\) \(\qquad\) D. \(6\)

问题：21 已知实数 \(\lambda>0\) ，向量 \(\vec{a},\vec{b},\vec{c}\) 的模都等于 \(\lambda\) ，且 \(\vec{a}\cdot\vec{b}=0, \vec{c}\cdot\vec{b}=1,\vec{c}\cdot\vec{a}=2\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：22 （多选）已知 \(O\) 为坐标原点，点 \(P_1(\cos\alpha,\sin\alpha)\) ， \(P_2(\cos\beta,-\sin\beta)\) ， \(P_3(\cos(\alpha+\beta)\) ，\(\sin(\alpha+\beta))\) ， \(A(1,0)\) 则：

A. \(|\overrightarrow{OP_1}|=|\overrightarrow{OP_2}|\) \(\qquad\qquad\qquad\quad\) B. \(|\overrightarrow{AP_1}|=|\overrightarrow{AP_2}|\)

C. \(\overrightarrow{OA}\cdot\overrightarrow{OP_3}=\overrightarrow{OP_1}\cdot\overrightarrow{OP_2}\) \(\qquad\qquad\) D. \(\overrightarrow{OA}\cdot\overrightarrow{OP_1}=\overrightarrow{OP_2}\cdot\overrightarrow{OP_3}\)

问题：23 设 \(\boldsymbol{e_1},\boldsymbol{e_2}\) 为单位向量，满足 \(|2\boldsymbol{e_1}-\boldsymbol{e_2}|\leq\sqrt{2}, \boldsymbol{a}=\boldsymbol{e_1}+\boldsymbol{e_2}, \boldsymbol{b}=3\boldsymbol{e_1}+\boldsymbol{e_2}\) 设 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角为 \(\theta\) ，则 \(\cos^2\theta\) 的最小值为 \(\_\_\_\_\_\_\)

问题：24 已知 \(\boldsymbol{a_1},\boldsymbol{b_1},\boldsymbol{a_2},\boldsymbol{b_2},\cdots, \boldsymbol{b_k}\) 是平面内两两互不相等的向量，若 \(|\boldsymbol{a_1}-\boldsymbol{a_2}|=1\) ，且 \(|\boldsymbol{a_i}-\boldsymbol{b_j}|\in\{1,2\}\) （其中 \(i=1,2, j=1,2,\cdots,k\) ），则 \(k\) 最大值为 \(\_\_\_\_\_\_\)

问题：25 已知向量 \(\boldsymbol{a},\boldsymbol{b}\) 满足 \(|\boldsymbol{a}|=5, |\boldsymbol{b}|=6, \boldsymbol{a}\cdot\boldsymbol{b}=-6\) ，则 \(\cos\langle\boldsymbol{a},\boldsymbol{a}+\boldsymbol{b}\rangle=\)

A. \(-\dfrac{31}{35}\) \(\qquad\) B. \(\dfrac{19}{35}\) \(\qquad\) C. \(\dfrac{17}{35}\) \(\qquad\) D. \(\dfrac{19}{35}\)

问题：26 已知单位向量 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角为 \(60^\circ\) ，则在下列向量中，与 \(\boldsymbol{b}\) 垂直的是

A. \(\boldsymbol{a}+2\boldsymbol{b}\) \(\qquad\) B. \(2\boldsymbol{a}+\boldsymbol{b}\) \(\qquad\) \(\boldsymbol{a}-2\boldsymbol{b}\) \(\qquad\) D. \(2\boldsymbol{a}-\boldsymbol{b}\)

问题：27 已知单位向量 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角为 \(45^\circ\) ， \(k\boldsymbol{a}-b\) 与 \(a\) 垂直，则 \(k=\_\_\_\_\_\_\)

问题：28 设 \(\boldsymbol{a},\boldsymbol{b}\) 为单位向量，且 \(|\boldsymbol{a}+\boldsymbol{b}|=1\) ，则 $|-|=

问题：29 已知正方形 \(ABCD\) 的边长为 1 。当每个 \(\lambda_i (i=1,2,3,4,5,6)\) 取遍 \(\pm 1\) 时， \(\left|\lambda_1\overrightarrow{AB}+\lambda_2\overrightarrow{BC}+\lambda_3\overrightarrow{CD}+\lambda_4\overrightarrow{DA}+\lambda_5\overrightarrow{AC}+\lambda_6\overrightarrow{BD}\right|\) 的最小值是 \(\_\_\_\_\_\_\_\) ，最大值是 \(\_\_\_\_\_\_\_\)

问题：30 已知 \(\boldsymbol{a},\boldsymbol{b}\) 为单位向量，且 \(\boldsymbol{a}\cdot\boldsymbol{b}=0\) ，若 \(\boldsymbol{c}=2\boldsymbol{a}-\sqrt{5}\boldsymbol{b}\) ，则 \(\cos\langle\boldsymbol{a},\boldsymbol{c}\rangle=\_\_\_\_\_\_\)

问题：31 已知向量 \(\boldsymbol{a}=(2,3)\) ， \(\boldsymbol{b}=(3,2)\) ，则 \(\left|\boldsymbol{a}-\boldsymbol{b}\right|=\)

A. \(\sqrt{2}\) \(\qquad\) B. \(2\) \(\qquad\) C. \(5\sqrt{2}\) \(\qquad\) D. \(50\)

问题：32 已知 \(\overrightarrow{AB}=(2,3)\) ， \(\overrightarrow{AC}=(3,t)\) ， \(\left|\overrightarrow{BC}\right|=1\) ，则 \(\overrightarrow{AB}\cdot\overrightarrow{BC}=\)

  1. \(-3\) \(\qquad\) (B) \(-2\) \(\qquad\) (C) \(2\) \(\qquad\) (D) \(3\)

问题：33 已知非零向量 \(\boldsymbol{a},\boldsymbol{b}\) 满足 \(\left|\boldsymbol{a}\right|=2\left|\boldsymbol{b}\right|\) ，且 \((\boldsymbol{a}-\boldsymbol{b})\perp\boldsymbol{b}\) ，则 \(\boldsymbol{a}\) 与 \(\boldsymbol{b}\) 的夹角为

  1. \(\dfrac{\pi}{6}\) \(\qquad\) (B) \(\dfrac{\pi}{3}\) \(\qquad\) (C) \(\dfrac{2\pi}{3}\) \(\qquad\) (D) \(\dfrac{5\pi}{6}\)

问题：34 设点 \(A,B,C\) 不共线，则 “\(\overrightarrow{AB}\) 与 \(\overrightarrow{AC}\) 的夹角为锐角” 是 \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|>\left|\overrightarrow{BC}\right|\) 的

  1. 充分而不必要条件 \(\qquad\) (B) 必要而不充分条件

  2. 充分必要条件 \(\qquad\qquad\) (D) 既不充分也不必要条件

问题：35 设 \(\boldsymbol{a}\)，\(\boldsymbol{b}\) 均为单位向量，则 “\(\left|\boldsymbol{a}-3\boldsymbol{b}\right|=\left|3\boldsymbol{a}+\boldsymbol{b}\right|\)” 是 “\(\boldsymbol{a}\perp\boldsymbol{b}\)” 的

  1. 充分而不必要条件 \(\quad\) (B) 必要而不充分条件

  2. 充分必要条件 \(\qquad\quad\) (D) 既不充分也不必要条件

几何综合

问题：36 （多选）在正三棱柱 \(ABC-A_1B_1C_1\) 中， \(AB=AA_1=1\) ，点 \(P\) 满足 \(\overrightarrow{BP}=\lambda\overrightarrow{BC}+\mu\overrightarrow{BB_1}\) ，其中 \(\lambda\in[0,1],\mu\in[0,1]\) ，则

A. 当 \(\lambda=1\) 时， \(\triangle{AB_1P}\) 的周长为定值

B. 当 \(\mu=1\) 时， 三棱锥 \(P-A_1BC\) 的体积为定值

C. 当 \(\lambda=\dfrac{1}{2}\) 时，有且仅有一个点，使得 \(A_1P\perp BP\)

D. 当 \(\mu=\dfrac{1}{2}\) 时，有且仅有一个点，使得 \(A_1B\perp\)平面\(AB_1P\)

问题：37 在四边形 \(ABCD\) 中， \(AD\parallel BC, AB=2\sqrt{3}, AD=5, \angle{A}=30^\circ\) ，点 \(E\) 在线段 \(CB\) 的延长线上，且 \(AE=BE\) ，则 \(\overrightarrow{BD}\cdot\overrightarrow{AE}=\_\_\_\_\_\_\)

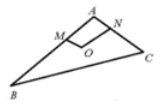
问题：38 在如图的平面图形中，已知 \(OM=1\) ， \(ON=2\) ， \(\angle MON=120^\circ\) ， \(\overrightarrow{BM}=2\overrightarrow{MA}\) ，\(CN=2NA\) ，则 \(\overrightarrow{BC}\cdot\overrightarrow{OM}\) 的值为

  1. \(-15\) \(\qquad\) (B) \(-9\) \(\qquad\) (C) \(-6\) \(\qquad\) (D) \(0\)

问题：39 已知 \(P\) 是边长为 \(2\) 的正六边形 \(ABCDEF\) 内的一点，则 \(\overrightarrow{AP}\cdot\overrightarrow{AB}\) 的取值范围是

A. \((-2,6)\) \(\qquad\) B. \((-6,2)\) \(\qquad\) C. \((-2,4)\) \(\qquad\) D. \((-4,6)\)

三点共线

问题：40 已知正方形 \(ABCD\) 的边长为 \(2\) ，点 \(P\) 满足 \(\overrightarrow{AP}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\) ，则 \(|\overrightarrow{PD}|=\_\_\_\_\_\_\) ； \(\overrightarrow{PB}\cdot\overrightarrow{PD}=\_\_\_\_\_\_\) 。

问题：41 在 \(\triangle{ABC}\) 中， \(AB=4, AC=3, \angle{BAC}=90^\circ\) ，\(D\) 在边 \(BC\) 上，延长 \(AD\) 到 \(P\) ，使得 \(AP=9\) ，若 \(\overrightarrow{PA}=m\overrightarrow{PB}+\left(\dfrac{3}{2}-m\right)\overrightarrow{PC}\) （ \(m\) 为常数），则 \(CD\) 的长度是 \(\_\_\_\_\_\_\)

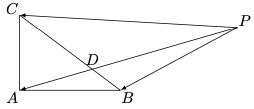
问题：42 过 \(y^2=4x\) 的焦点 \(F\) 并垂直于 \(x\) 轴的直线分别与 \(y^2=4x\) 交于 \(A\)、\(B\) ，\(A\) 在 \(B\) 上方， \(M\) 为抛物线上一点， \(\overrightarrow{OM}=\lambda\overrightarrow{OA}+(\lambda-2)\overrightarrow{OB}\) ，则 \(\lambda=\_\_\_\_\_\_\)

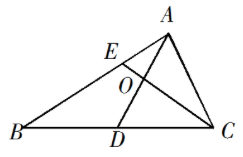
问题：43 如图，在 \(\triangle ABC\) 中， \(D\) 是 \(BC\) 的中点， \(E\) 在边 \(AB\) 上， \(BE=2EA\) ， \(AD\) 与 \(CE\) 交于点 \(O\) 。若 \(\overrightarrow{AB}\cdot\overrightarrow{AC}=6\overrightarrow{AO}\cdot\overrightarrow{EC}\) ，则 \(\dfrac{AB}{AC}\) 的值是 \(\_\_\_\_\_\_\_\)

问题：44 在 \(\triangle ABC\) 中， \(AD\) 为 \(BC\) 边上的中线， \(E\) 为 \(AD\) 的中点，则 \(\overrightarrow{EB}=\)

  1. \(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}\) \(\qquad\) (B) \(\dfrac{1}{4}\overrightarrow{AB}-\dfrac{3}{4}\overrightarrow{AC}\)

  2. \(\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\) \(\qquad\) (D) \(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\)

等内积圆

问题：45 在 \(\triangle{ABC}\) 中， \(AC=3, BC=4, \angle{C}=90^\circ\) 。 \(P\) 为 \(\triangle{ABC}\) 所在平面内的动点，且 \(PC=1\) ，则 \(\overrightarrow{PA}\cdot\overrightarrow{PB}\) 的取值范围是

A. \([-5,3]\) \(\qquad\) B. \([-3,5]\) \(\qquad\) C. \([-6,4]\) \(\qquad\) D. \([-4,6]\)

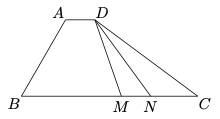
问题：46 如图，在四边形 \(ABCD\) 中， \(\angle{B}=60^\circ, AB=3, BC=6\) ，且 \(\overrightarrow{AD}=\lambda\overrightarrow{BC}\) ， \(\overrightarrow{AD}\cdot\overrightarrow{AB}=-\dfrac{3}{2}\) ，则实数 \(\lambda\) 的值为 \(\_\_\_\_\_\_\) 。若 \(M, N\) 是线段 \(BC\) 上的动点，且 \(|\overrightarrow{MN}|=1\) ，则 \(\overrightarrow{DM}\cdot\overrightarrow{DN}\) 的最小值为 \(\_\_\_\_\_\_\) 。

问题：47 在平面内， \(A,B\) 是两个定点， \(C\) 是动点。若 \(\overrightarrow{AC}\cdot\overrightarrow{BC}=1\) ，则点 \(C\) 的轨迹为

A. 圆 \(\qquad\) B. 椭圆 \(\qquad\) C. 抛物线 \(\qquad\) D. 直线

问题：48 如图，在平面四边形 \(ABCD\) 中， \(AB\perp BC\)，\(AD\perp CD\)，\(\angle BAD=120^\circ\)，\(AB=AD=1\)。若点 \(E\) 为边 \(CD\) 上的动点，则 \(\overrightarrow{AE}\cdot\overrightarrow{BE}\) 的最小值为

  1. \(\dfrac{21}{16}\) \(\qquad\) (B) \(\dfrac{3}{2}\) \(\qquad\) (C) \(\dfrac{25}{16}\) \(\qquad\) (D) \(3\)

问题：49 已知 \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{e}\) 是平面向量， \(\boldsymbol{e}\) 是单位向量。若非零向量 \(\boldsymbol{a}\) 与 \(\boldsymbol{e}\) 的夹角为 \(\dfrac{\pi}{3}\) ，向量 \(\boldsymbol{b}\) 满足 \(\boldsymbol{b}^2-4\boldsymbol{e}\cdot\boldsymbol{b}+3=0\) ，则 \(\left|\boldsymbol{a}-\boldsymbol{b}\right|\) 的最小值是

  1. \(\sqrt{3}-1\) \(\qquad\) (B) \(\sqrt{3}+1\) \(\qquad\) (C) 2 \(\qquad\) (D) \(2-\sqrt{3}\)

二次函数

问题：50 设点 \(P\) 在单位圆的内接正八边形 \(A_1A_2\cdots A_8\) 的边 \(A_1A_2\) 上，则 \(\overrightarrow{PA_1}^2+\overrightarrow{PA_2}^2+\cdots\overrightarrow{PA_8}^2\) 的取值范围是 \(\_\_\_\_\_\_\)

问题：51 已知平面向量 \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}(\boldsymbol{c}\neq0)\) 满足 \(|a|=1,|b|=2\) , \(a\cdot b=0, (a-b)\cdot c=0\) 。记向量 \(\boldsymbol{d}\) 在 \(\boldsymbol{a},\boldsymbol{b}\) 方向上的投影分别为 \(x,y\), \(\boldsymbol{d}-\boldsymbol{a}\) 在 \(\boldsymbol{c}\) 方向上的投影为 \(z\) ，则 \(x^2+y^2+z^2\) 的最小值是 \(\_\_\_\_\_\_\)

向量真题汇编（编年体）

问题：52 在 \(\triangle{ABC}\) 中，点 \(D\) 在边 \(AB\) 上， \(BD=2DA\) ，记 \(\overrightarrow{CA}=\boldsymbol{m}, \overrightarrow{CD}=\boldsymbol{n}\) ，则 \(\overrightarrow{CB}=\_\_\_\_\_\_\)

A. \(3\boldsymbol{m}-2\boldsymbol{n}\) \(\qquad\) B. \(-2\boldsymbol{m}+3\boldsymbol{n}\) \(\qquad\) C. \(3\boldsymbol{m}+2\boldsymbol{n}\) \(\qquad\) D. \(2\boldsymbol{m}+3\boldsymbol{n}\)

问题：53 已知向量 \(\boldsymbol{a}=(3,4)\)，\(\boldsymbol{b}=(1,0)\) ， \(\boldsymbol{c}=\boldsymbol{a}+t\boldsymbol{b}\) ， 若 \(\langle\boldsymbol{a},\boldsymbol{c}\rangle=\langle\boldsymbol{b},\boldsymbol{c}\rangle\) ，则实数 \(t=\)

A. \(-6\) \(\qquad\) B. \(-5\) \(\qquad\) C. \(5\) \(\qquad\) D. \(6\)

问题：54 已知向量 \(\boldsymbol{a},\boldsymbol{b}\) 满足 \(|\boldsymbol{a}|=1,|\boldsymbol{b}|=\sqrt{3},|\boldsymbol{a}-2\boldsymbol{b}|=3\) ，则 \(\boldsymbol{a}\cdot\boldsymbol{b}=\)

A. \(-2\) \(\qquad\) B. \(-1\) \(\qquad\) C. \(1\) \(\qquad\) D. \(2\)

问题：55 已知向量 \(\boldsymbol{a}=(2,1),\boldsymbol{b}=(-2,4)\) ，则 \(|\boldsymbol{a}-\boldsymbol{b}|=\)

A. \(2\) \(\qquad\) B. \(3\) \(\qquad\) C. \(4\) \(\qquad\) D. \(5\)

问题：56 设向量 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角的余弦值为 \(\dfrac{1}{3}\) ，且 \(|\boldsymbol{a}|=1,|\boldsymbol{b}|=3\) ，则 \((2\boldsymbol{a}+\boldsymbol{b})\cdot\boldsymbol{b}=\_\_\_\_\_\_\)

问题：57 已知向量 \(\boldsymbol{a}=(m,3),\boldsymbol{b}=(1,m+1)\) 。若 \(\boldsymbol{a}\perp\boldsymbol{b}\) ，则 \(m=\_\_\_\_\_\_\) 。

问题：58 在 \(\triangle{ABC}\) 中， \(AC=3, BC=4, \angle{C}=90^\circ\) 。 \(P\) 为 \(\triangle{ABC}\) 所在平面内的动点，且 \(PC=1\) ，则 \(\overrightarrow{PA}\cdot\overrightarrow{PB}\) 的取值范围是

A. \([-5,3]\) \(\qquad\) B. \([-3,5]\) \(\qquad\) C. \([-6,4]\) \(\qquad\) D. \([-4,6]\)

问题：59 已知实数 \(\lambda>0\) ，向量 \(\vec{a},\vec{b},\vec{c}\) 的模都等于 \(\lambda\) ，且 \(\vec{a}\cdot\vec{b}=0, \vec{c}\cdot\vec{b}=1,\vec{c}\cdot\vec{a}=2\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：60 在 \(\triangle{ABC}\) 中，\(\overrightarrow{CA}=a\)，\(\overrightarrow{CB}=b\) ，\(D\) 是 \(AC\) 的中点；\(\overrightarrow{CB}=2\overrightarrow{BE}\)。试用 \(a,b\) 表示 \(\overrightarrow{DE}\) ：\(\_\_\_\_\_\_\) ；若 \(\overrightarrow{AB}\perp\overrightarrow{DE}\) ，求 \(\angle{C}\) 的最小值为 \(\_\_\_\_\_\_\) 。

问题：61 设点 \(P\) 在单位圆的内接正八边形 \(A_1A_2\cdots A_8\) 的边 \(A_1A_2\) 上，则 \(\overrightarrow{PA_1}^2+\overrightarrow{PA_2}^2+\cdots\overrightarrow{PA_8}^2\) 的取值范围是 \(\_\_\_\_\_\_\)

问题：62 已知平面向量 \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}(\boldsymbol{c}\neq0)\) 满足 \(|a|=1,|b|=2\) , \(a\cdot b=0, (a-b)\cdot c=0\) 。记向量 \(\boldsymbol{d}\) 在 \(\boldsymbol{a},\boldsymbol{b}\) 方向上的投影分别为 \(x,y\), \(\boldsymbol{d}-\boldsymbol{a}\) 在 \(\boldsymbol{c}\) 方向上的投影为 \(z\) ，则 \(x^2+y^2+z^2\) 的最小值是 \(\_\_\_\_\_\_\)

问题：63 若向量 a,b 满足 \(|a|=3,\ |a-b|=5,\ a\cdot b=1\) ，则 \(|b|=\_\_\_\_\_\_\) 。

问题：64 已知向量 \(\vec{a}=(3,1),\vec{b}=(1,0),\vec{c}=\vec{a}+k\vec{b}\) ，若 \(\vec{a}\perp\vec{c}\) ，则 \(k=\_\_\_\_\_\_\)

问题：65 已知向量 \(\vec{a}=(2,5)\)，\(\vec{b}=(\lambda,4)\) ，若 \(\vec{a}\parallel\vec{b}\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：66 已知向量 \(\vec{a}=(1,3)\)，\(\vec{b}=(3,4)\) ，若 \((\vec{a}-\lambda\vec{b})\perp\vec{b}\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：67 （多选）已知 \(O\) 为坐标原点，点 \(P_1(\cos\alpha,\sin\alpha)\) ， \(P_2(\cos\beta,-\sin\beta)\) ， \(P_3(\cos(\alpha+\beta)\) ，\(\sin(\alpha+\beta))\) ， \(A(1,0)\) 则：

A. \(|\overrightarrow{OP_1}|=|\overrightarrow{OP_2}|\) \(\qquad\qquad\qquad\quad\) B. \(|\overrightarrow{AP_1}|=|\overrightarrow{AP_2}|\)

C. \(\overrightarrow{OA}\cdot\overrightarrow{OP_3}=\overrightarrow{OP_1}\cdot\overrightarrow{OP_2}\) \(\qquad\qquad\) D. \(\overrightarrow{OA}\cdot\overrightarrow{OP_1}=\overrightarrow{OP_2}\cdot\overrightarrow{OP_3}\)

问题：68 （多选）在正三棱柱 \(ABC-A_1B_1C_1\) 中， \(AB=AA_1=1\) ，点 \(P\) 满足 \(\overrightarrow{BP}=\lambda\overrightarrow{BC}+\mu\overrightarrow{BB_1}\) ，其中 \(\lambda\in[0,1],\mu\in[0,1]\) ，则

A. 当 \(\lambda=1\) 时， \(\triangle{AB_1P}\) 的周长为定值

B. 当 \(\mu=1\) 时， 三棱锥 \(P-A_1BC\) 的体积为定值

C. 当 \(\lambda=\dfrac{1}{2}\) 时，有且仅有一个点，使得 \(A_1P\perp BP\)

D. 当 \(\mu=\dfrac{1}{2}\) 时，有且仅有一个点，使得 \(A_1B\perp\)平面\(AB_1P\)

问题：69 如图（原题给图了，其实没啥意义，放水而已），正方形 \(ABCD\) 的边长为 \(3\) ，则 \(\overrightarrow{AB}\cdot\overrightarrow{AC}=\_\_\_\_\_\_\)

问题：70 设 \(\boldsymbol{e_1},\boldsymbol{e_2}\) 为单位向量，满足 \(|2\boldsymbol{e_1}-\boldsymbol{e_2}|\leq\sqrt{2}, \boldsymbol{a}=\boldsymbol{e_1}+\boldsymbol{e_2}, \boldsymbol{b}=3\boldsymbol{e_1}+\boldsymbol{e_2}\) 设 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角为 \(\theta\) ，则 \(\cos^2\theta\) 的最小值为 \(\_\_\_\_\_\_\)

问题：71 在 \(\triangle{ABC}\) 中，\(D\) 是 \(AB\) 边上的中点，则 \(\overrightarrow{CB}=\)

A. \(2\overrightarrow{CD}+\overrightarrow{CA}\) \(\qquad\) B. \(\overrightarrow{CD}-\overrightarrow{2CA}\) \(\qquad\) C. \(2\overrightarrow{CD}-\overrightarrow{CA}\) \(\qquad\) D. \(\overrightarrow{CD}+2\overrightarrow{CA}\)

问题：72 已知 \(P\) 是边长为 \(2\) 的正六边形 \(ABCDEF\) 内的一点，则 \(\overrightarrow{AP}\cdot\overrightarrow{AB}\) 的取值范围是

A. \((-2,6)\) \(\qquad\) B. \((-6,2)\) \(\qquad\) C. \((-2,4)\) \(\qquad\) D. \((-4,6)\)

问题：73 如图，在四边形 \(ABCD\) 中， \(\angle{B}=60^\circ, AB=3, BC=6\) ，且 \(\overrightarrow{AD}=\lambda\overrightarrow{BC}\) ， \(\overrightarrow{AD}\cdot\overrightarrow{AB}=-\dfrac{3}{2}\) ，则实数 \(\lambda\) 的值为 \(\_\_\_\_\_\_\) 。若 \(M, N\) 是线段 \(BC\) 上的动点，且 \(|\overrightarrow{MN}|=1\) ，则 \(\overrightarrow{DM}\cdot\overrightarrow{DN}\) 的最小值为 \(\_\_\_\_\_\_\) 。

问题：74 已知 \(\boldsymbol{a_1},\boldsymbol{b_1},\boldsymbol{a_2},\boldsymbol{b_2},\cdots, \boldsymbol{b_k}\) 是平面内两两互不相等的向量，若 \(|\boldsymbol{a_1}-\boldsymbol{a_2}|=1\) ，且 \(|\boldsymbol{a_i}-\boldsymbol{b_j}|\in\{1,2\}\) （其中 \(i=1,2, j=1,2,\cdots,k\) ），则 \(k\) 最大值为 \(\_\_\_\_\_\_\)

问题：75 在平面内， \(A,B\) 是两个定点， \(C\) 是动点。若 \(\overrightarrow{AC}\cdot\overrightarrow{BC}=1\) ，则点 \(C\) 的轨迹为

A. 圆 \(\qquad\) B. 椭圆 \(\qquad\) C. 抛物线 \(\qquad\) D. 直线

问题：76 已知向量 \(\boldsymbol{a},\boldsymbol{b}\) 满足 \(|\boldsymbol{a}|=5, |\boldsymbol{b}|=6, \boldsymbol{a}\cdot\boldsymbol{b}=-6\) ，则 \(\cos\langle\boldsymbol{a},\boldsymbol{a}+\boldsymbol{b}\rangle=\)

A. \(-\dfrac{31}{35}\) \(\qquad\) B. \(\dfrac{19}{35}\) \(\qquad\) C. \(\dfrac{17}{35}\) \(\qquad\) D. \(\dfrac{19}{35}\)

问题：77 已知单位向量 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角为 \(60^\circ\) ，则在下列向量中，与 \(\boldsymbol{b}\) 垂直的是

A. \(\boldsymbol{a}+2\boldsymbol{b}\) \(\qquad\) B. \(2\boldsymbol{a}+\boldsymbol{b}\) \(\qquad\) \(\boldsymbol{a}-2\boldsymbol{b}\) \(\qquad\) D. \(2\boldsymbol{a}-\boldsymbol{b}\)

问题：78 已知单位向量 \(\boldsymbol{a},\boldsymbol{b}\) 的夹角为 \(45^\circ\) ， \(k\boldsymbol{a}-b\) 与 \(a\) 垂直，则 \(k=\_\_\_\_\_\_\)

问题：79 设向量 \(\boldsymbol{a}=(1,-1), \boldsymbol{b}=(m+1,2m-4)\) ，若 \(\boldsymbol{a}\perp\boldsymbol{b}\) ，则 \(m=\_\_\_\_\_\_\)

问题：80 设 \(\boldsymbol{a},\boldsymbol{b}\) 为单位向量，且 \(|\boldsymbol{a}+\boldsymbol{b}|=1\) ，则 \(|\boldsymbol{a}-\boldsymbol{b}|=\_\_\_\_\_\_\)

问题：81 在 \(\triangle{ABC}\) 中， \(AB=4, AC=3, \angle{BAC}=90^\circ\) ，\(D\) 在边 \(BC\) 上，延长 \(AD\) 到 \(P\) ，使得 \(AP=9\) ，若 \(\overrightarrow{PA}=m\overrightarrow{PB}+\left(\dfrac{3}{2}-m\right)\overrightarrow{PC}\) （ \(m\) 为常数），则 \(CD\) 的长度是 \(\_\_\_\_\_\_\)

问题：82 已知正方形 \(ABCD\) 的边长为 \(2\) ，点 \(P\) 满足 \(\overrightarrow{AP}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\) ，则 \(|\overrightarrow{PD}|=\_\_\_\_\_\_\) ； \(\overrightarrow{PB}\cdot\overrightarrow{PD}=\_\_\_\_\_\_\) 。

问题：83 已知正方形 \(ABCD\) 的边长为 1 。当每个 \(\lambda_i (i=1,2,3,4,5,6)\) 取遍 \(\pm 1\) 时， \(\left|\lambda_1\overrightarrow{AB}+\lambda_2\overrightarrow{BC}+\lambda_3\overrightarrow{CD}+\lambda_4\overrightarrow{DA}+\lambda_5\overrightarrow{AC}+\lambda_6\overrightarrow{BD}\right|\) 的最小值是 \(\_\_\_\_\_\_\_\) ，最大值是 \(\_\_\_\_\_\_\_\)

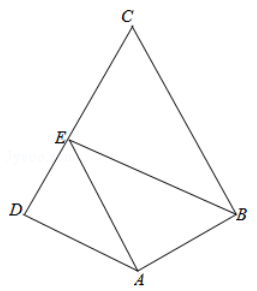
问题：8485 在四边形 \(ABCD\) 中， \(AD\parallel BC, AB=2\sqrt{3}, AD=5, \angle{A}=30^\circ\) ，点 \(E\) 在线段 \(CB\) 的延长线上，且 \(AE=BE\) ，则 \(\overrightarrow{BD}\cdot\overrightarrow{AE}=\_\_\_\_\_\_\)

问题：86 过 \(y^2=4x\) 的焦点 \(F\) 并垂直于 \(x\) 轴的直线分别与 \(y^2=4x\) 交于 \(A\)、\(B\) ，\(A\) 在 \(B\) 上方， \(M\) 为抛物线上一点， \(\overrightarrow{OM}=\lambda\overrightarrow{OA}+(\lambda-2)\overrightarrow{OB}\) ，则 \(\lambda=\_\_\_\_\_\_\)

问题：87 已知直线方程 \(2x-y+c=0\) 的一个方向向量 \(\overrightarrow{d}\) 可以是

A. \((2,-1)\) \(\qquad\) B. \((2,1)\) \(\qquad\) C. \((-1,2)\) \(\qquad\) D. \((1,2)\)

问题：88 已知向量 \(\boldsymbol{a}=(2,2),\boldsymbol{b}=(-8,6)\) ，则 \(\cos\langle\boldsymbol{a},\boldsymbol{b}\rangle=\_\_\_\_\_\_\_\)

问题：89 已知 \(\boldsymbol{a},\boldsymbol{b}\) 为单位向量，且 \(\boldsymbol{a}\cdot\boldsymbol{b}=0\) ，若 \(\boldsymbol{c}=2\boldsymbol{a}-\sqrt{5}\boldsymbol{b}\) ，则 \(\cos\langle\boldsymbol{a},\boldsymbol{c}\rangle=\_\_\_\_\_\_\)

问题：90 已知向量 \(\boldsymbol{a}=(2,3)\) ， \(\boldsymbol{b}=(3,2)\) ，则 \(\left|\boldsymbol{a}-\boldsymbol{b}\right|=\)

A. \(\sqrt{2}\) \(\qquad\) B. \(2\) \(\qquad\) C. \(5\sqrt{2}\) \(\qquad\) D. \(50\)

问题：91 已知 \(\overrightarrow{AB}=(2,3)\) ， \(\overrightarrow{AC}=(3,t)\) ， \(\left|\overrightarrow{BC}\right|=1\) ，则 \(\overrightarrow{AB}\cdot\overrightarrow{BC}=\)

  1. \(-3\) \(\qquad\) (B) \(-2\) \(\qquad\) (C) \(2\) \(\qquad\) (D) \(3\)

问题：92 已知非零向量 \(\boldsymbol{a},\boldsymbol{b}\) 满足 \(\left|\boldsymbol{a}\right|=2\left|\boldsymbol{b}\right|\) ，且 \((\boldsymbol{a}-\boldsymbol{b})\perp\boldsymbol{b}\) ，则 \(\boldsymbol{a}\) 与 \(\boldsymbol{b}\) 的夹角为

  1. \(\dfrac{\pi}{6}\) \(\qquad\) (B) \(\dfrac{\pi}{3}\) \(\qquad\) (C) \(\dfrac{2\pi}{3}\) \(\qquad\) (D) \(\dfrac{5\pi}{6}\)

问题：93 如图，在 \(\triangle ABC\) 中， \(D\) 是 \(BC\) 的中点， \(E\) 在边 \(AB\) 上， \(BE=2EA\) ， \(AD\) 与 \(CE\) 交于点 \(O\) 。若 \(\overrightarrow{AB}\cdot\overrightarrow{AC}=6\overrightarrow{AO}\cdot\overrightarrow{EC}\) ，则 \(\dfrac{AB}{AC}\) 的值是 \(\_\_\_\_\_\_\_\)

问题：94 已知向量 \(\boldsymbol{a}=(-4,3)\) ， \(\boldsymbol{b}=(6,m)\) ，且 \(\boldsymbol{a} \perp \boldsymbol{b}\) ， 则 \(m=\_\_\_\_\_\_\_\_\)

问题：95 设点 \(A,B,C\) 不共线，则 “\(\overrightarrow{AB}\) 与 \(\overrightarrow{AC}\) 的夹角为锐角” 是 \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|>\left|\overrightarrow{BC}\right|\) 的

  1. 充分而不必要条件 \(\qquad\)(B) 必要而不充分条件

  2. 充分必要条件 \(\qquad\qquad\) (D) 既不充分也不必要条件

问题：96 已知向量 \(\boldsymbol a, \boldsymbol b\) 满足 \(\left|\boldsymbol a\right|=1\) ， \(\boldsymbol a \cdot \boldsymbol b=-1\) ，则 \(\boldsymbol a \cdot (2\boldsymbol a-\boldsymbol b)=\)

  1. 4 \(\qquad\)(B) 3 \(\qquad\)(C) 2 \(\qquad\)(D) 0

问题：97 已知向量 \(\boldsymbol{a}=(1,2)\) ， \(\boldsymbol{b}=(2,-2)\) ， \(\boldsymbol{c}=(1,\lambda)\) 。若 \(\boldsymbol{c}\parallel(2\boldsymbol{a}+\boldsymbol{b})\) ， 则\(\lambda=\_\_\_\_\_\_\_\)

问题：98 设 \(\boldsymbol{a}\)，\(\boldsymbol{b}\) 均为单位向量，则 “\(\left|\boldsymbol{a}-3\boldsymbol{b}\right|=\left|3\boldsymbol{a}+\boldsymbol{b}\right|\)” 是 “\(\boldsymbol{a}\perp\boldsymbol{b}\)” 的

  1. 充分而不必要条件 \(\quad\)(B) 必要而不充分条件

  2. 充分必要条件 \(\qquad\quad\) (D) 既不充分也不必要条件

问题：99 在 \(\triangle ABC\) 中， \(AD\) 为 \(BC\) 边上的中线， \(E\) 为 \(AD\) 的中点，则 \(\overrightarrow{EB}=\)

  1. \(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}\) \(\qquad\) (B) \(\dfrac{1}{4}\overrightarrow{AB}-\dfrac{3}{4}\overrightarrow{AC}\)

  2. \(\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\) \(\qquad\) (D) \(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\)

问题：100 在如图的平面图形中，已知 \(OM=1\)， \(ON=2\)， \(\angle MON=120^\circ\)， \(\overrightarrow{BM}=2\overrightarrow{MA}\) ，\(CN=2NA\) ，则 \(\overrightarrow{BC}\cdot\overrightarrow{OM}\) 的值为

  1. \(-15\) \(\qquad\) (B) \(-9\) \(\qquad\) (C) \(-6\) \(\qquad\) (D) \(0\)

问题：101 如图，在平面四边形 \(ABCD\) 中， \(AB\perp BC\)，\(AD\perp CD\)，\(\angle BAD=120^\circ\)，\(AB=AD=1\)。若点 \(E\) 为边 \(CD\) 上的动点，则 \(\overrightarrow{AE}\cdot\overrightarrow{BE}\) 的最小值为

  1. \(\dfrac{21}{16}\) \(\qquad\)(B) \(\dfrac{3}{2}\) \(\qquad\)(C) \(\dfrac{25}{16}\) \(\qquad\)(D) \(3\)

问题：102 已知 \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{e}\) 是平面向量， \(\boldsymbol{e}\) 是单位向量。若非零向量 \(\boldsymbol{a}\) 与 \(\boldsymbol{e}\) 的夹角为 \(\dfrac{\pi}{3}\) ，向量 \(\boldsymbol{b}\) 满足 \(\boldsymbol{b}^2-4\boldsymbol{e}\cdot\boldsymbol{b}+3=0\) ，则 \(\left|\boldsymbol{a}-\boldsymbol{b}\right|\) 的最小值是

  1. \(\sqrt{3}-1\) \(\qquad\)(B) \(\sqrt{3}+1\) \(\qquad\)(C) 2 \(\qquad\)(D) \(2-\sqrt{3}\)

问题：103 设向量 \(\boldsymbol{a}=(1,0)\) ， \(\boldsymbol{b}=(-1,m)\) ，且 \(\boldsymbol{a} \perp (m\boldsymbol{a}-\boldsymbol{b})\) ， 则 \(m=\_\_\_\_\_\_\_\_\) 。

  1. 2022 全国高考乙卷理科数学第 3 题↩︎

  2. 2022 全国高考乙卷文科数学第 3 题↩︎

  3. 2022 全国高考甲卷理科数学第 13 题↩︎

  4. 2022 全国高考甲卷文科数学第 13 题↩︎

  5. 2021 全国甲卷 文科数学第 13 题↩︎

  6. 2021 全国甲卷 理科数学第 14 题↩︎

  7. 2021 全国乙卷 文科数学第 13 题↩︎

  8. 2021 全国乙卷 理科数学第 14 题↩︎

  9. 2021 全国乙卷 理科数学第 14 题↩︎

  10. 2021 全国乙卷 理科数学第 14 题↩︎

  11. 2020 全国新高考 II 卷数学第 3 题↩︎

  12. 2020 全国高考 I 卷文科数学第 14 题↩︎

  13. 2019 上海高考数学第 13 题↩︎

  14. 2019 全国高考 III 卷文科数学 第 13 题↩︎

  15. 2019 北京卷文科数学 第 9 题↩︎

  16. 2018 全国II卷 理科数学第 4 题 文科数学第 4 题↩︎

  17. 2018 全国III卷 文科数学第 13 题↩︎

  18. 2018 北京卷文科数学 第 9 题↩︎

  19. 2022 全国新高考 I 卷数学第 3 题↩︎

  20. 2022 全国新高考 II 卷数学第 4 题↩︎

  21. 2022 上海高考数学第 11 题↩︎

  22. 2021 全国新高考 I 卷数学第 10 题↩︎

  23. 2020 浙江数学第 17 题↩︎

  24. 2020 上海高考数学第 12 题↩︎

  25. 2020 全国高考 III 卷理科数学第 6 题↩︎

  26. 2020 全国高考 II 卷文科数学第 5 题↩︎

  27. 2020 全国高考 II 卷理科数学第 13 题↩︎

  28. 2020 全国高考 I 卷理科数学第 14 题↩︎

  29. 2019 浙江高考文科数学第 17 题↩︎

  30. 2019 全国高考 III 卷理科数学 第 13 题↩︎

  31. 2019 全国II卷 文科数学第 3 题↩︎

  32. 2019 全国II卷 理科数学第 3 题↩︎

  33. 2019 全国I卷 理科数学第 7 题 文科数学第 8 题↩︎

  34. 2019 北京卷 理科数学 第 7 题↩︎

  35. 2018 北京卷 理科数学第 6 题↩︎

  36. 2021 全国新高考 I 卷数学第 12 题↩︎

  37. 2019 天津高考文科数学第 14 题}\footnote{2019 天津高考理科数学第 14 题↩︎

  38. 2018 天津卷文科数学 第 8 题↩︎

  39. 2020 全国新高考 I 卷数学第 7 题↩︎

  40. 2020 北京高考数学第 13 题↩︎

  41. 2020 江苏高考数学第 13 题↩︎

  42. 2019 上海高考数学第 9 题↩︎

  43. 2019 江苏卷 数学第 12 题↩︎

  44. 2018 全国I卷 理科数学第 6 题 文科数学第 7 题↩︎

  45. 2022 北京高考数学第 10 题↩︎

  46. 2020 天津高考数学第 15 题↩︎

  47. 2020 全国高考 III 卷文科数学第 6 题↩︎

  48. 2018 天津卷 理科数学第 8 题↩︎

  49. 2018 浙江卷 数学第 9 题↩︎

  50. 2022 浙江高考数学第 17 题↩︎

  51. 2021 浙江数学第 17 题↩︎

  52. 2022 全国新高考 I 卷数学第 3 题↩︎

  53. 2022 全国新高考 II 卷数学第 4 题↩︎

  54. 2022 全国高考乙卷理科数学第 3 题↩︎

  55. 2022 全国高考乙卷文科数学第 3 题↩︎

  56. 2022 全国高考甲卷理科数学第 13 题↩︎

  57. 2022 全国高考甲卷文科数学第 13 题↩︎

  58. 2022 北京高考数学第 10 题↩︎

  59. 2022 上海高考数学第 11 题↩︎

  60. 2022 天津高考数学第 14 题↩︎

  61. 2022 浙江高考数学第 17 题↩︎

  62. 2021 浙江数学第 17 题↩︎

  63. 2021 全国甲卷 文科数学第 13 题↩︎

  64. 2021 全国甲卷 理科数学第 14 题↩︎

  65. 2021 全国乙卷 文科数学第 13 题↩︎

  66. 2021 全国乙卷 理科数学第 14 题↩︎

  67. 2021 全国新高考 I 卷数学第 10 题↩︎

  68. 2021 全国新高考 I 卷数学第 12 题↩︎

  69. 2021 上海数学第 4 题↩︎

  70. 2020 浙江数学第 17 题↩︎

  71. 2020 全国新高考 II 卷数学第 3 题↩︎

  72. 2020 全国新高考 I 卷数学第 7 题↩︎

  73. 2020 天津高考数学第 15 题↩︎

  74. 2020 上海高考数学第 12 题↩︎

  75. 2020 全国高考 III 卷文科数学第 6 题↩︎

  76. 2020 全国高考 III 卷理科数学第 6 题↩︎

  77. 2020 全国高考 II 卷文科数学第 5 题↩︎

  78. 2020 全国高考 II 卷理科数学第 13 题↩︎

  79. 2020 全国高考 I 卷文科数学第 14 题↩︎

  80. 2020 全国高考 I 卷理科数学第 14 题↩︎

  81. 2020 江苏高考数学第 13 题↩︎

  82. 2020 北京高考数学第 13 题↩︎

  83. 2019 浙江高考文科数学第 17 题↩︎

  84. 2019 天津高考文科数学第 14 题↩︎

  85. 2019 天津高考理科数学第 14 题↩︎

  86. 2019 上海高考数学第 9 题↩︎

  87. 2019 上海高考数学第 13 题↩︎

  88. 2019 全国高考 III 卷文科数学 第 13 题↩︎

  89. 2019 全国高考 III 卷理科数学 第 13 题↩︎

  90. 2019 全国II卷 文科数学第 3 题↩︎

  91. 2019 全国II卷 理科数学第 3 题↩︎

  92. 2019 全国I卷 理科数学第 7 题 文科数学第 8 题↩︎

  93. 2019 江苏卷 数学第 12 题↩︎

  94. 2019 北京卷文科数学 第 9 题↩︎

  95. 2019 北京卷 理科数学 第 7 题↩︎

  96. 2018 全国II卷 理科数学第 4 题 文科数学第 4 题↩︎

  97. 2018 全国III卷 文科数学第 13 题↩︎

  98. 2018 北京卷 理科数学第 6 题↩︎

  99. 2018 全国I卷 理科数学第 6 题 文科数学第 7 题↩︎

  100. 2018 天津卷文科数学 第 8 题↩︎

  101. 2018 天津卷 理科数学第 8 题↩︎

  102. 2018 浙江卷 数学第 9 题↩︎

  103. 2018 北京卷文科数学 第 9 题↩︎