三角函数真题汇编

三角函数真题汇编

问题：¹ 下列区间中，函数 \(f(x)=7\sin(x-\dfrac{\pi}{6})\) 的单调递增区间是：

A. \((0,\dfrac{\pi}{2})\) \(\qquad\) B. \((\dfrac{\pi}{2},\pi)\) \(\qquad\) C. \((\pi,\dfrac{3\pi}{2})\) \(\qquad\) D. \((\dfrac{3\pi}{2},2\pi)\)

问题：² 函数 \(f(x)=\sin\dfrac{x}{3}+\cos\dfrac{x}{3}\) 的最小正周期和最大值分别是：

A. \(3\pi\) 和 \(\sqrt{2}\) \(\qquad\) B. \(3\pi\) 和 \(2\) \(\qquad\) C. \(6\pi\) 和 \(\sqrt{2}\) \(\qquad\) D. \(6\pi\) 和 \(2\)

问题：³ \(\cos^2\dfrac{\pi}{12}-\cos^2\dfrac{5\pi}{12}=\)

A. \(\dfrac{1}{2}\) \(\qquad\) B. \(\dfrac{\sqrt{3}}{2}\) \(\qquad\) C. \(\dfrac{\sqrt{2}}{2}\) \(\qquad\) D.\(\dfrac{\sqrt{3}}{2}\)

问题：⁴ 若 \(\tan\theta=-2\) ，则 \(\dfrac{\sin\theta(1+\sin2\theta)}{\sin\theta+\cos\theta}=\)

A. \(-\dfrac{6}{5}\) \(\qquad\) B. \(-\dfrac{2}{5}\) \(\qquad\) C. \(\dfrac{2}{5}\) \(\qquad\) D. \(\dfrac{6}{5}\)

问题：⁵⁶ 若 \(\alpha\in(0,\dfrac{\pi}{2})\) ， \(\tan2\alpha=\dfrac{\cos\alpha}{2-\sin\alpha}\) ，则 \(\tan\alpha=\)

A. \(\dfrac{\sqrt{15}}{15}\) \(\qquad\) B. \(\dfrac{\sqrt{5}}{5}\) \(\qquad\) C. \(\dfrac{\sqrt{5}}{3}\) \(\qquad\) D. \(\dfrac{\sqrt{15}}{3}\)

问题：⁷ 在 \(\triangle{ABC}\) 中，已知 \(B=120^\circ,\ AC=\sqrt{19},\ AB=2\) ，则 \(BC=\)

A. \(1\)B. \(\sqrt{2}\)C. \(\sqrt{5}\)D. \(3\)

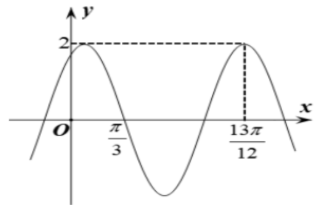
问题：⁸ 已知函数 \(f(x)=2\cos(\omega x+\phi)\) 的部分图像如图 1 所示，则 \(f\left(\dfrac{\pi}{2}\right)=\_\_\_\_\_\_\)

\(f(x)=2\cos(\omega x+\phi)\)

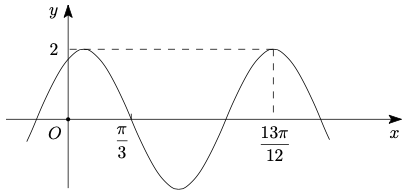
问题：⁹ 已知函数 \(f(x)=2\cos(\omega x+\phi)\) 的部分图像如图所示，则满足条件 \((f(x)-f(-\dfrac{7\pi}{4}))\cdot(f(x)-f(\dfrac{4\pi}{3}))>0\) 的最小正整数 \(x\) 为 \(\_\_\_\_\_\_\)

\(f(x)=2\cos(\omega x+\phi)\)

问题：¹⁰ 把函数 \(y=f(x)\) 图像上所有点的横坐标缩短到原来的 \(\dfrac{1}{2}\) 倍，纵坐标不变，再把所得曲线向右平移 \(\dfrac{\pi}{3}\) 个单位长度，得到函数 \(y=\sin(x-\dfrac{\pi}{4})\) 的图像，则 \(f(x)=\)

A. \(\sin(\dfrac{x}{2}-\dfrac{7\pi}{12})\)B. \(\sin(\dfrac{x}{2}+\dfrac{\pi}{12})\)

C. \(\sin(2x-\dfrac{7\pi}{12})\)D. \(\sin(2x+\dfrac{\pi}{12})\)

问题：¹¹¹² 记 \(\triangle{ABC}\) 的内角 \(A,B,C\) 的对边分别为 \(a,b,c\) ，面积为 \(\sqrt{3}\) ，\(B=60^\circ\) ， \(a^2+c^2=3ac\) ，则 \(b=\_\_\_\_\_\_\)

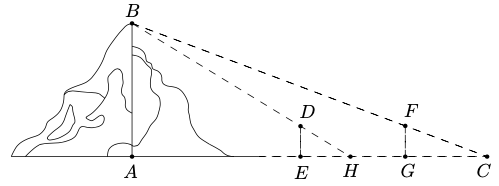
问题：¹³ 魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高。如图，点 \(E, H, G\) 在水平线 \(AC\) 上， \(DE\) 和 \(FG\) 是两个垂直于水平面且等高的测量标杆的高度，称为“表高”， \(EG\) 称为“表距”， \(GC\) 和 \(EH\) 都称为“表目距”，\(GC\) 与 \(EH\) 的差称为“表目距的差”. 则海岛的高 \(AB =\)

A. \(\dfrac{表高}\times\mbox{表距}}{\mbox{表目距的差}}+\mbox{表高}\) \(\qquad\) B. \(\dfrac{\mbox{表高}\times\mbox{表距}}{\mbox{表目距的差}}-\mbox{表高\)

C. \(\dfrac{表高}\times\mbox{表距}}{\mbox{表目距的差}}+\mbox{表距}\) \(\qquad\) D. \(\dfrac{\mbox{表高}\times\mbox{表距}}{\mbox{表目距的差}}-\mbox{表距\)

问题：¹⁴ 已知函数 \(f(x)=\cos x-\cos 2x\) ，则该函数是：

A. 奇函数，最大值为 \(2\) \(\qquad\qquad\) B. 偶函数，最大值 \(2\)

C. 奇函数，最大值为 \(\dfrac{9}{8}\) \(\qquad\qquad\) D. 偶函数，最大值为 \(\dfrac{9}{8}\)

问题：¹⁵ 已知函数 \(f(x)=\cos^2 x-\sin^2 x\) ，则

A. \(f(x)\) 在 \(\left(-\dfrac{\pi}{2},-\dfrac{\pi}{2}\right)\) 上单调递增

B. \(f(x)\) 在 \(\left(-\dfrac{\pi}{4},\dfrac{\pi}{12}\right)\) 上单调递增

C. \(f(x)\) 在 \(\left(0,\dfrac{\pi}{3}\right)\) 上单调递减

D. \(f(x)\) 在 \(\left(\dfrac{\pi}{4},\dfrac{7\pi}{12}\right)\) 上单调递增

问题：¹⁶ 在 \(\triangle{ABC}\) 中， \(AC=3\) ， \(BC=4\) ， \(\angle{C}=90^\circ\) 。 \(P\) 为 \(\triangle{ABC}\) 所在平面内的点，且 \(PC=1\) ，则 \(\overrightarrow{PA}\cdot\overrightarrow{PB}\) 的取值范围是：

A. \([-5,3]\) \(\quad\qquad\) B. \([-3,5]\) \(\quad\qquad\) C. \([-6,4]\) \(\quad\qquad\) D. \([-4,6]\)

问题：¹⁷ 若函数 \(f(x)=A\sin x-\sqrt{3}\cos x\) 的一个零点为 \(\dfrac{\pi}{3}\) ，则 \(A=\_\_\_\_\_\_\) ；\(f\left(\dfrac{\pi}{12}\right)=\_\_\_\_\_\_\) 。

问题：¹⁸ 在 \(\triangle{ABC}\) 中， \((a+c)(\sin A-\sin C)=b(\sin A-\sin B)\) ，则 \(\angle C=(\ \ )\)

A. \(\dfrac{\pi}{6}\) \(\qquad\qquad\) B. \(\dfrac{\pi}{3}\) \(\qquad\qquad\) C. \(\dfrac{2\pi}{3}\) \(\qquad\qquad\) D. \(\dfrac{5\pi}{6}\)

问题：¹⁹ 已知命题 \(P\)：若 \(\alpha,\beta\) 为第一象限角，且 \(\alpha>\beta\) ，则 \(\tan\alpha>\tan\beta\) 。能说明 \(P\) 为假命题的一组 \(\alpha,\beta\) 的值为 \(\alpha=\_\_\_\_\_\_,\beta=\_\_\_\_\_\_\)

问题：²⁰ 已知 \(f(x)=\sin \omega x(\omega>0)\) ， \(f(x_1)=-1\) ， \(f(x_2)=1\) ， \(\left|x_1-x_2\right|_{min}=\dfrac{\pi}{2}\) ， 则 \(\omega=(\ \ )\)

A. \(1\) \(\qquad\qquad\) B. \(2\) \(\qquad\qquad\) C. \(3\) \(\qquad\qquad\) D. \(4\)

问题：²¹ 已知边长为 \(4\) 的正方形为底面的四棱锥，四条侧棱分别为 \(4,4,2\sqrt{2},2\sqrt{2}\) ，则该四棱锥的高为：

A. \(\dfrac{\sqrt{2}}{2}\) \(\qquad\qquad\) B. \(\dfrac{\sqrt{3}}{2}\) \(\qquad\qquad\) C. \(2\sqrt{3}\) \(\qquad\qquad\) D. \(\sqrt{3}\)

问题：²² 设函数 \(f(x)=\sin(\omega x)+\cos(\omega x) (\omega>0)\) ，若 \(f(x+\pi)=f(x)\) 恒成立，且 \(f(x)\) 在 \(\left[0,\dfrac{\pi}{4}\right]\) 上存在零点，则 \(\omega\) 的最小值：

A. \(8\) \(\qquad\qquad\) B. \(6\) \(\qquad\qquad\) C. \(4\) \(\qquad\qquad\) D. \(3\)

问题：²³ 已知平面直角坐标系 \(xOy\) 中，\(\left|\overrightarrow{OA}\right|=\left|\overrightarrow{OB}\right|=\sqrt{2}\) , \(\left|\overrightarrow{AB}=2\right|\) ，设 \(C(3,4)\) 。则 \(\left|2\overrightarrow{CA}+\overrightarrow{AB}\right|\) 的取值范围是：

A. \(\left[6,14\right]\) \(\quad\qquad\) B. \(\left[6,12\right]\) \(\quad\qquad\) C. \(\left[8 ,14\right]\) \(\quad\qquad\) D. \(\left[8,12\right]\)

问题：²⁴ 已知 \(\alpha,\beta\in\left[0,2\pi\right]\) ，且 \(\sin(\alpha+\beta)=\sin(\alpha-\beta)\) ， \(\cos(\alpha+\beta)\neq\cos(\alpha-\beta)\) ，写出满足条件的一组 \(\alpha=\_\_\_\_\_\_\) ， \(\beta=\_\_\_\_\_\_\) 。

问题：²⁵ 关于定义域为 \(\mathbb{R}\) 的函数 \(f(x)\) ，以下说法正确的有 \(\_\_\_\_\_\_\)

1. 存在在 \(\mathbb{R}\) 上单调递增的函数 \(f(x)\) ，使得 \(f(x)+f(2x)=-x\) 恒成立；

2. 存在在 \(\mathbb{R}\) 上单调递减的函数 \(f(x)\) ，使得 \(f(x)+f(2x)=-x\) 恒成立；

3. 使得 \(f(x)+f(-x)=\cos(x)\) 恒成立的函数 \(f(x)\) 存在且有无穷多个；

4. 使得 \(f(x)-f(-x)=\cos(x)\) 恒成立的函数 \(f(x)\) 存在且有无穷多个。

问题：²⁶ 记 \(\triangle{ABC}\) 的内角 \(A,B,C\) 的对边分别为 \(a,b,c\) 。已知 \(b^2=ac\) ，点 \(D\) 在边 \(AC\) 上， \(BD\sin\angle{ABC}=a\sin{C}\) 。

1. 证明： \(BD=b\) ；

2. 若 \(AD=2DC\) ，求 \(\cos\angle{ABC}\) 。

问题：²⁷ 在 \(\triangle{ABC}\) 中， \(\sin 2C=\sqrt{3}\sin C\) 。

1. 求 \(\angle{C}\) ；

2. 若 \(b=6\) ，且 \(\triangle{ABC}\) 的面积为 \(6\sqrt{3}\) ，求 \(\triangle{ABC}\) 的周长。

问题：²⁸ 设函数 \(f(x)=\sin\omega x\cos\psi+\cos\omega x\sin\phi\) ， \(\left(\omega>0,|\psi|<\dfrac{\pi}{2}\right)\)。

1. 若 \(f(0)=-\dfrac{\sqrt{3}}{2}\) ， 求 \(\psi\) 的值；

2. 已知 \(f(x)\) 在区间 \(\left[-\dfrac{\pi}{3},\dfrac{2\pi}{3}\right]\) 上单调递增， \(f\left(\dfrac{2\pi}{3}\right)=1\) ，再从以下三个条件中选择一个作为已知，使函数 \(f(x)\) 存在，求 \(\omega,\psi\) 的值。

\(f\left(\dfrac{\pi}{3}\right)=\sqrt{2}\); \(f\left(-\dfrac{\pi}{3}\right)=-1\)；

\(f(x)\) 在区间 \(\left[-\dfrac{\pi}{2},-\dfrac{\pi}{3}\right]\) 上单调递减。

问题：²⁹ 在 \(\triangle{ABC}\) 中， \(a=7\) ， \(A\) 为钝角， \(\sin 2B=\dfrac{\sqrt{3}}{7}b\cos B\) 。

1. 求 \(A\) ；

2. 在以下三个条件中选择一个作为已知，求 \(\triangle{ABC}\) 的面积。

\(b=7\); \(\cos C=\dfrac{13}{14}\)； \(c\sin A=\dfrac{5}{2}\sqrt{3}\)；

问题：³⁰ 在 \(\triangle{ABC}\) 中， \(\cos A=-\dfrac{1}{3}\) ， \(a\sin C=4\sqrt{2}\) 。

1. 求 \(c\) ；

2. 在以下三个条件中选择一个作为已知，使得 \(\triangle{ABC}\) 存在，求 \(BC\) 的高。

\(a=6\); \(b\sin C=\dfrac{10\sqrt{2}}{3}\)； \(\triangle{ABC}\) 的面积为 \(10\sqrt{2}\) 。

立体几何真题汇编

问题：³¹ 某四面体的三视图如图所示, 该四面体的表面积为：

A. \(\dfrac{3+\sqrt{3}}{2}\) \(\qquad\) B. \(\dfrac{1}{2}\) \(\qquad\) C. \(\dfrac{1+\sqrt{3}}{2}\) \(\qquad\) D. \(\dfrac{\sqrt{3}}{2}\)

问题：³² 已知一个圆锥的底面半径为 \(6\)，其体积为 \(30\pi\) ，则该圆锥的侧面积为 \(\_\_\_\_\_\_\)

问题：³³ 已知圆锥的底面半径为 \(\sqrt{2}\) ，其侧面展开图为一个半圆，则该圆锥的母线长为：

A. \(2\) \(\qquad\) B. \(2\sqrt{2}\) \(\qquad\) C. \(4\) \(\qquad\) D. \(4\sqrt{2}\)

问题：³⁴ \(2020\) 年 \(12\) 月 \(8\) 日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为 \(8848.86\) (单位: \(\mathrm{m}\))，三角高程测量法是珠峰高程测量方法之一。如图是三角高程测量法的一个示意图，现有 \(A\)，\(B\)，\(C\) 三点，且 \(A\)，\(B\)，\(C\) 在同一水平面上的投影 \(A', B', C'\) 满足 \(\angle{A'C'B'}=45^\circ\)， \(\angle{A'B'C'}=60^\circ\) 。由 \(C\) 点测得 \(B\) 点的仰角为 \(15^\circ\) ，\(BB'\) 与 \(CC'\) 的差为 \(100\) 。由 \(B\) 点测得 \(A\) 点的仰角为 \(45^\circ\) ，则 \(A,C\) 两点到水平面 \(A'B'C'\) 的高度差 \(AA'−CC'\) 约为：(\(\sqrt{3}\approx1.732\))

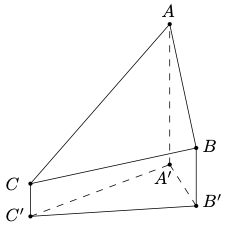
A. \(346\)B. \(373\)C. \(446\)D. \(473\)

问题：³⁵ 已知 \(A,B,C\) 是半径为 \(1\) 的球 \(O\) 的球面上的三个点，且 \(AC\perp BC\) ， \(AC=BC=1\) ，则三棱锥 \(O-ABC\) 的体积为：

A. \(\dfrac{\sqrt{2}}{12}\) \(\qquad\) B. \(\dfrac{\sqrt{3}}{12}\) \(\qquad\) C. \(\dfrac{\sqrt{2}}{4}\) \(\qquad\) D. \(\dfrac{\sqrt{3}}{4}\)

问题：³⁶ 在正方体 \(ABCD-A_1B_1C_1D_1\) 中， \(P\) 为 \(B_1D_1\) 的中点，则直线 \(PB\) 与 \(AD_1\) 所成的角为：

A. \(\dfrac{\pi}{2}\) \(\qquad\) B. \(\dfrac{\pi}{3}\) \(\qquad\) C. \(\dfrac{\pi}{4}\) \(\qquad\) D. \(\dfrac{\pi}{6}\)

问题：³⁷³⁸ 以图 为正视图，在图 中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为 \(\_\_\_\_\_\_\)

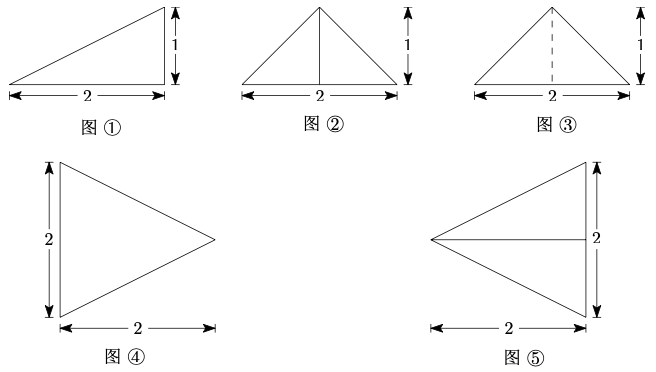
问题：³⁹ （多选）在正三棱柱 \(ABC-A_1B_1C_1\) 中， \(AB=AA_1=1\) ，点 \(P\) 满足 \(\overrightarrow{BP}=\lambda\overrightarrow{BC}+\mu\overrightarrow{BB_1}\) ，其中 \(\lambda\in[0,1]\) ，\(\mu\in[0,1]\) ，则：

A. 当 \(\lambda=1\) 时，\(\triangle{AB_1P}\) 的周长为定值

B. 当 \(\mu=1\) 时，三棱锥 \(P-A_1BC\) 的体积为定值

C. 当 \(\lambda=\dfrac{1}{2}\) 时，有且只有一个点 \(P\) ，使得 \(A_1P\perp BP\)

4. 当 \(\mu=\dfrac{1}{2}\) 时，有且只有一个点 \(P\) ，使得 \(A_1B\perp平面AB_1P\)

问题：⁴⁰ 已知直三棱柱 \(ABC-A_1B_1C_1\) 中，侧面 \(AA_1B_1B\) 为正方形， \(AB=BC=2\) ，\(E,F\) 分别为 \(AC\) 和 \(CC_1\) 的中点， \(BF\perp A_1B_1\) 。

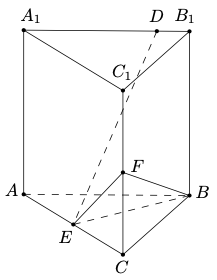
1. 求三棱锥 \(F-EBC\) 的体积；

2. 已知 \(D\) 为棱 \(A_1B_1\) 上的点，证明： \(BF\perp DE\) 。

问题：⁴¹ 已知直三棱柱 \(ABC-A_1B_1C_1\) 中，侧面 \(AA_1B_1B\) 为正方形， \(AB=BC=2\) ，\(E,F\) 分别为 \(AC\) 和 \(CC_1\) 的中点， \(D\) 为棱 \(A_1B_1\) 上的点 ， \(BF\perp A_1B_1\) 。

1. 证明： \(BF\perp DE\)；

2. 当 \(B_1D\) 为何值时，面 \(BB_1C1C\) 与面 \(DFE\) 所成的 二面角的正弦值最小。

问题：⁴² 如图，四棱锥 \(P-ABCD\) 的底面是矩形，\(PD\perp\)底面\(ABCD\) ，\(M\) 为 \(BC\) 的中点，且 \(PB\perp AM\) 。

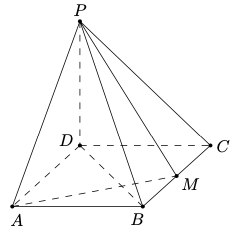
1. 证明：平面 \(PAM\perp\) 平面 \(PBD\) ；

2. 若 \(PD=DC=1\) ，求四棱锥 \(P-ABCD\) 的体积。

问题：⁴³ 如图，四棱锥 \(P-ABCD\) 的底面是矩形，\(PD\perp\)底面\(ABCD\) ，\(PD=DC=1\) ，\(M\) 为 \(BC\) 的中点，且 \(PB\perp AM\) 。

1. 求 \(BC\) ；

2. 求二面角 \(A-PM-B\) 的正弦值。

问题：⁴⁴ 如图，在三棱锥 \(A-BCD\) 中，平面\(ABD\perp\)平面\(BCD\) ， \(AB=AD\) ， \(O\) 为 \(BD\) 中点。

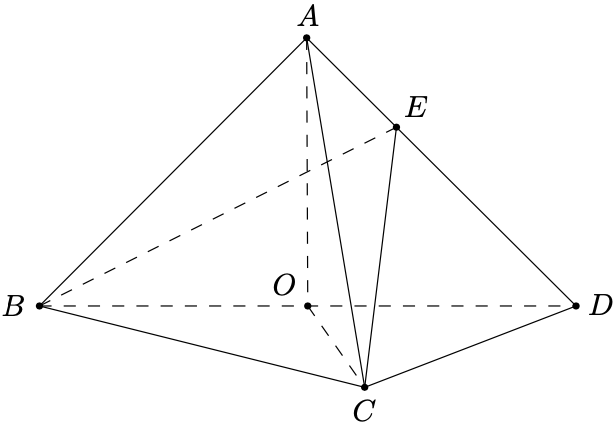
1. 证明：\(OA\perp CD\) ；

2. 若 \(\triangle{OCD}\) 是边长为 \(1\) 的等边三角形，点 \(E\) 在棱 \(AD\) 上， \(DE=2EA\) ，且二面角 \(E-BC-D\) 的大小为 \(45^\circ\) ，求三棱锥 \(A-BCD\) 的体积。