函数、不等式和导数真题汇编

函数选择填空真题汇编

问题：¹ 下列函数中，在区间 \((0,+\infty)\) 上单调递增的是：

A. \(f(x)=-\ln x\) \(\quad\quad\) B. \(f(x)=\dfrac{1}{2^x}\)

C. \(f(x)=-\dfrac{1}{x}\) \(\quad\) D. \(f(x)=3^{|x-1|}\)

问题：² \(\left(2x-\dfrac{1}{x}\right)\) 的展开式中 \(x\) 的系数为：

A. \(-80\) \(\quad\) B. \(-40\) \(\quad\) C. \(40\) \(\quad\) D. \(80\)

问题：³ 若 \(xy\neq0\) ，则 “\(x+y=0\)” 是 “\(\dfrac{y}{x}+\dfrac{x}{y}=-2\)” 的

A. 充分不必要条件 \(\quad\) B. 必要不充分条件

C. 充要条件 \(\quad\quad\) D. 既不充分也不必要条件

问题：⁴ 已知函数 \(f(x)=\dfrac{1}{1+2^x}\) ，则对任意实数 \(x\) ，有：

A. \(\dfrac{1}{2}\) \(\qquad\) B. \(-\dfrac{1}{2}\) \(\qquad\) C. \(1\) \(\qquad\) D. \(-1\)

问题：⁵ 函数 \(f(x)=\dfrac{1}{x}+\sqrt{1-x}\) 的定义域是 \(\_\_\_\_\_\_\)

问题：⁶ 设函数 \(f(x)=\begin{cases}-ax+1, x<a\\ (x-2)^2, x\geq a\end{cases}\) ，若 \(f(x)\) 存在最小值，则 \(a\) 的一个取值为 \(\_\_\_\_\_\_\) ； \(a\) 的最大值为 \(\_\_\_\_\_\_\) 。

问题：⁷ 已知 \(a,b\in\mathbb{R}\) ，若对任意 \(x\in\mathbb{R}\) ，\(a|x-b|+|x-4|-|2x-5|\geq0\) ，则：

A. \(a\leq1,b\geq3\) \(\quad\) B. \(a\leq1,b\leq3\)

C. \(a\geq1,b\geq3\) \(\quad\) D. \(a\geq1,b\leq3\)

问题：⁸ 已知 \(f(x)=\begin{cases}-x^2+2,x\leq1\\x+\dfrac{1}{x}-1,x\geq1\end{cases}\) ，则 \(f\left(f\left(\dfrac{1}{2}\right)\right)=\_\_\_\_\_\_\) ；若当 \(a\in[a,b]\) 时， \(1\leq f(x)\leq3\) ，则 \(b-a\) 的最大值为 \(\_\_\_\_\_\_\) 。

问题：⁹ 若函数 \(f(x)\) 的定义域为 \(\mathbb{R}\) ，且 \(f(x+y)+f(x-y)=f(x)f(y),f(y)=1\) ，则 \(\displaystyle\sum_{k=1}^{22}f(k)=\)

A. \(-3\) \(\qquad\) B. \(-2\) \(\qquad\) C. \(0\) \(\qquad\) D. \(1\)

问题：¹⁰ 设函数 \(f(x)\) 的定义域为 \([0,1]\) ，则“函数 \(f(x)\) 在 \([0,1]\) 上单调递增”是“函数 \(f(x)\) 在 \([0,1]\) 上的最大值为 \(f(1)\)”的：

A. 充分不必要条件 \(\qquad\) B. 必要不充分条件

C. 充分必要条件 \(\qquad\) D. 既不充分也不必要条件

问题：¹¹ 下列函数中是增函数的为

A. \(f(x)=-x\) \(\qquad\) B. \(f(x)=\left(\dfrac{2}{3}\right)^x\) \(\qquad\) C. \(f(x)=x^2\) \(\qquad\) D. \(\sqrt[3]{x}\)

问题：¹²¹³ 已知命题 \(p:\exists x\in\mathbb{R},\sin x<1\) ；命题 \(q:\forall x\in\mathbb{R},e^{|x|}\geq1\)，则下列命题中为真命题的是：

A. \(p\wedge q\) \(\qquad\) B. \(\neg p\wedge q\) \(\qquad\) C. \(p\wedge\neg q\) \(\qquad\) D. \(\neg(p\wedge q)\)

问题：¹⁴ 若 \(x,y\) 满足约束条件 \(\begin{cases}x+y\geq4\\x-y\leq2\\y\leq3\end{cases}\) ，则 \(z=3x+y\) 的最小值为：

A. \(18\) \(\qquad\) B. \(10\) \(\qquad\) C. \(6\) \(\qquad\) D. \(4\)

问题：¹⁵¹⁶ 青少年视力是社会普遍关注的问题，视力情况可借助视力表测量。通常用五分记录法和小数记录法记录视力数据，五分记录法的数据 \(L\) 和小数记录法的数据 \(V\) 满足 \(L=5+\lg V\) 。已知某同学视力的五分记录法的数据为 \(4.9\) ，则其视力的小数记录法的数据约为：(\(\sqrt[10]{10}\approx1.259\))

A. \(1.5\) \(\qquad\) B. \(1.2\) \(\qquad\) C. \(0.8\) \(\qquad\) D. \(0.6\)

问题：¹⁷¹⁸ 函数 \(f(x)=\dfrac{1-x}{1+x}\) ，则下列函数中为奇函数的是：

A. \(f(x-1)-1\) \(\qquad\) B. \(f(x-1)+1\)

C. \(f(x+1)-1\) \(\qquad\) D. \(f(x+1)+1\)

问题：¹⁹ 曲线 \(y=\dfrac{2x-1}{x+2}\) 在点 \((-1,-3)\) 处的切线方程为 \(\_\_\_\_\_\_\)

问题：²⁰ 设函数 \(f(x)\) 的定义域为 \(\mathbb{R}\) ， \(f(x+1)\) 为奇函数， \(f(x+2)\) 为偶函数，当 \(x\in[1,2]\) 时， \(f(x)=ax^2+b\) 。若 \(f(0)+f(3)=6\) ， 则 \(f\left(\dfrac{9}{2}\right)=\)

A. \(-\dfrac{9}{4}\) \(\qquad\) B. \(-\dfrac{3}{2}\) \(\qquad\) C. \(\dfrac{7}{4}\) \(\qquad\) D. \(\dfrac{5}{2}\)

问题：²¹ 设 \(f(x)\) 是定义域为 \(\mathbb{R}\) 的奇函数，且 \(f(1+x)=f(-x)\) 。若 \(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{3}\) ，则 \(f\left(\dfrac{5}{3}\right)=\)

A. \(-\dfrac{5}{3}\) \(\qquad\) B. \(-\dfrac{1}{3}\) \(\qquad\) C. \(\dfrac{1}{3}\) \(\qquad\) D. \(\dfrac{5}{3}\)

问题：²² 下列函数中最小值为 \(4\) 的是：

A. \(y=x^2+2x+4\) \(\qquad\) B. \(y=|\sin x|+\dfrac{4}{|\sin x|}\)

C. \(y=2^x+2^{2-x}\) \(\qquad\quad\) D. \(y=\ln x+\dfrac{4}{\ln x}\)

问题：²³²⁴ 设 \(a\neq0\) ，若 \(x=a\) 为函数 \(f(x)=a(x-a)^2(x-b)\) 的极大值点，则：

A. \(a<b\) \(\qquad\) B. \(a>b\) \(\qquad\) C. \(ab<a^2\) \(\qquad\) D. \(ab>a^2\)

问题：²⁵ 设 \(a=2\ln1.01,\ b=\ln1.02,\ c=\sqrt{1.04}-1\) ，则：

A. \(a<b<c\) \(\qquad\) B. \(b<c<a\) \(\qquad\) C. \(b<a<c\) \(\qquad\) D. \(c<a<b\)

问题：²⁶ 若过点 \((a,b)\) 可以作曲线 \(y=e^x\) 的两条切线，则：

A. \(e^b<a\) \(\qquad\) B. \(e^a<b\) \(\qquad\) C. \(0<a<e^b\) \(\qquad\) D. \(0<b<e^a\)

问题：²⁷ 已知函数 \(f(x)=x^3(a\cdot2^{x}-2^{-x})\) 是偶函数，则 \(a=\_\_\_\_\_\_\)

问题：²⁸ 函数 \(f(x)=|2x-1|-2\ln x\) 的最小值为 \(\_\_\_\_\_\_\)

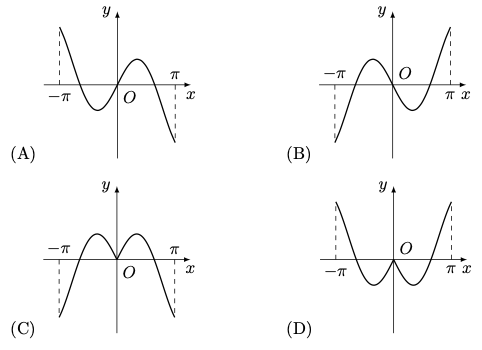
问题：²⁹ 函数 \(y=x\cos x+\sin x\) 在区间 \([-\pi,\pi]\) 的图像为：

问题：³⁰ 已知 \(a,b\in\mathbb{R}\) 且 \(ab\neq0\) ，若 \((x-a)(x-b)(x-2a-b)\geq0\) 在 \(x\geq0\) 上恒成立，则

A. \(a<0\) \(\qquad\) B. \(a>0\) \(\qquad\) C. \(b<0\) \(\qquad\) D. \(b>0\)

问题：³¹ 已知函数 \(f(x)=\lg(x^2-4x-5)\) 在 \((a,+\infty)\) 上单调递增，则 \(a\) 的取值范围是：

A. \((2,+\infty)\) \(\qquad\) B. \([2,+\infty)\) \(\qquad\) C. \((5,+\infty)\) \(\qquad\) D. \([5,+\infty)\)

问题：³²³³ 若定义在 \(\mathbb{R}\) 的奇函数 \(f(x)\) 在 \((-\infty,0)\) 单调递减，且 \(f(2)=0\) ，则满足 \(xf(x-1)\geq0\) 的 \(x\) 取值范围是：

A. \([-1,1]\cup[3,+\infty)\) \(\qquad\) B. \([-3,-1]\cup[0,1]\)

C. \([-1,0]\cup[1,+\infty)\) \(\qquad\) D. \([-1,0]\cup[1,3]\)

问题：³⁴³⁵ 已知 \(a>0,b>0\) ，且 \(a+b=1\) ，则：

A. \(a^2+b^2\geq\dfrac{1}{2}\) \(\qquad\qquad\) B. \(2^{a-b}>\dfrac{1}{2}\)

C. \(\log_{2}a+\log_{2}b\geq-2\) \(\qquad\) D. \(\sqrt{a}+\sqrt{b}\leq\sqrt{2}\)

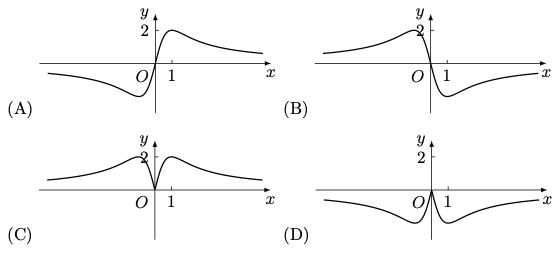
问题：³⁶ 函数 \(y=\dfrac{4x}{x^2+1}\) 的图像大致为：

问题：³⁷ 设 \(a=3^0.7, b=\left(\dfrac{1}{3}\right)^{-0.8}, c=\log_{0.7}0.8\) ，则 \(a,b,c\) 的大小关系为：

A. \(a<b<c\) \(\qquad\) B. \(b<a<c\)

C. \(b<c<a\) \(\qquad\) D. \(c<a<b\)

问题：³⁸ 已知函数 \(f(x)=\begin{cases}x^3,x\geq0\\-x, x<0\end{cases}\) ，若函数 \(g(x)=f(x)-\|kx^2-2x\|, (k\in\mathbb{R})\) 恰有四个零点，则 \(k\) 的取值范围是：

A. \(\left(-\infty,-\dfrac{1}{2}\right)\cup\left(2\sqrt{2},+\infty\right)\) \(\qquad\) B. \(\left(-\infty,-\dfrac{1}{2}\right)\cup\left(0,2\sqrt{2}\right)\)

C. \(\left(-\infty,0\right)\cup\left(0,2\sqrt{2}\right)\) \(\qquad\) D. \(\left(-\infty,-\dfrac{1}{2}\right)\cup\left(2\sqrt{2},+\infty\right)\)

问题：³⁹ 已知 \(a>0,b>0\) ，且 \(ab=1\) ，则 \(\dfrac{1}{2a}+\dfrac{1}{2b}+\dfrac{8}{a+b}\) 的最小值为 \(\_\_\_\_\_\_\)

问题：⁴⁰ 若 \(a,b\in\mathbb{R}\) ，则下列不等式中，恒成立的是：

A. \(a^2+b^2\leq2ab\) \(\quad\qquad\) B. \(a^2+b^2\geq-2ab\)

C. \(a+b\geq2\sqrt{|ab|}\) \(\qquad\) D. \(a+b\geq-2\sqrt{|ab|}\)

问题：⁴¹ 对于定义在 \(\mathbb{R}\) 上的函数 \(y=f(x)\) ，考察以下性质：

\(p\) ：存在非零实数 \(a\) ，使得 \(f(x+a)<f(x)+f(a)\) 对任意的 \(x\in\mathbb{R}\) 恒成立；

\(q_1\) ：\(y=f(x)\) 单调递减，且 \(f(x)\) 恒大于 \(0\) ；

\(q_2\) ：\(y=f(x)\) 单调递增，且存在 \(x_0<0\) ，使得 \(f(x_0)=0\) 。

关于上述性质，以下判断正确的是：

A. \(q_1,q_2\) 都是 \(p\) 的充分条件

B. \(q_1,q_2\) 中仅 \(q_1\) 是 \(p\) 的充分条件

C. \(q_1,q_2\) 中仅 \(q_2\) 是 \(p\) 的充分条件

D. \(q_1,q_2\) 都不是 \(p\) 的充分条件

导数（大题）真题汇编

问题：⁴² 已知函数 \(f(x)=e^x\ln(1+x)\)

• [(1)] 求曲线 \(y=f(x)\) 在点 \((0,f(0))\) 处的切线方程；
• [(2)] 设 \(g(x)=f'(x)\) ，讨论函数 \(g(x)\) 在 \([0,+\infty)\) 上的单调性；
• [(3)] 证明：对任意的 \(s,t\in(0,+\infty)\) ，有 \(f(s+t)>f(s)+f(t)\)

解：

1. \(f(0)=0\)，\(f'(x)=\dfrac{e^x}{1+x}+e^x\ln(1+x)\)，\(f'(0)=1\)

切线方程为 \(y=x\)

2. \(g(x)\) 的第二项 \(e^x\ln(1+x)\) 单调递增。判断其第一项的单调性：

当 \(x>0\) 时，\(\left(\dfrac{e^x}{1+x}\right)'=\dfrac{xe^x}{(1+x)^2}>0\)

因此 \(g(x)\) 在 \([0,+\infty)\) 上单调递增。

3. 综合第一问和第二问，可以看到 \(f(x)\) 是个凸函数，本问要求证明的性质只由凸函数就可以保证。所以不要扯细节，只需证明：\(f(s+t)-f(s)>f(t)-f(0)\)，即证 \(f(x+t)-f(t)\) 单调递增：

☐

问题：⁴³ 已知函数 \(f(x)=\dfrac{3-2x}{x^2+a}\)

• [(1)] 若 \(a=0\) ，求 \(y=f(x)\) 在 \((1,f(1))\) 处的切线方程；
• [(2)] 若函数在 \(x=-1\) 处取得极值，求 \(f(x)\) 的单调区间，以及最大值和最小值。

解： 这题送分题啊

问题：⁴⁴ 已知函数 \(f(x)=12-x^2\)

• [(1)] 求曲线 \(y=f(x)\) 的斜率等于 \(-2\) 的直线方程；
• [(2)] 设曲线 \(y=f(x)\) 在点 \((t,f(t))\) 处的切线与坐标轴围成的三角形的面积为 \(s(t)\) ，求 \(s(t)\) 的最小值。

问题：⁴⁵ 已知函数 \(f(x)=\dfrac{1}{4}x^3-x^2+x\)

• [(1)] 求曲线 \(y=f(x)\) 的斜率为 \(1\) 的切线方程；
• [(2)] 当 \(x\in[-2,4]\) 时，求证： \(x-6\leq f(x)\leq x\) ；
• [(3)] 设 \(F(x)=|f(x)-(x+a)|\quad(a\in\mathbb{R})\) ，记 \(F(x)\) 在区间 \([-2,4]\) 上的最大值为 \(M(a)\) 。当 \(M(a)\) 最小时，求 \(a\) 的值。

问题：⁴⁶ 设函数 \(f(x)=[ax^2-(4a+1)x+4a+3]e^x\) 。

• [(1)] 若曲线 \(y=f(x)\) 在点 \((1,f(1))\) 处的切线与 \(x\) 轴平行，求 \(a\) ；
• [(2)] 若 \(f(x)\) 在 \(x=2\) 处取得极小值，求 \(a\) 的取值范围。

问题：⁴⁷ 已知函数 \(f(x)=e^x\cos x-x\) 。

• [(1)] 求曲线 \(y=f(x)\) 在点 \((0,f(x))\) 处的切线方程；
• [(2)] 求函数 \(f(x)\) 在区间 \(\left[0,\dfrac{\pi}{2}\right]\) 上的最大值和最小值。

问题：⁴⁸ 设函数 \(f(x)=xe^{a-x}+bx\) ，曲线 \(y=f(x)\) 在点 \((2,f(x))\) 处的切线方程为 \(y=(e-1)x+4\) 。

• [(1)] 求 \(a,b\) 的值；
• [(2)] 求 \(f(x)\) 的单调区间；

问题：⁴⁹ 设函数 \(f(x)=x^3+ax^2+bx+c\) 。

• [(1)] 求曲线 \(y=f(x)\) 在点 \((0,f(x))\) 处的切线方程；
• [(2)] 设 \(a=b=4\) ，若函数 \(f(x)\) 有三个不同零点，求 \(c\) 的取值范围；
• [(3)] 求证： \(a^2-3b>0\) 是 \(f(x)\) 有三个不同零点的必要而不充分条件。

问题：⁵⁰ 已知函数 \(f(x)=\dfrac{1+x}{1-x}\)

• [(1)] 求曲线 \(y=f(x)\) 在点 \((0,f(x))\) 处的切线方程；
• [(2)] 求证：当 \(x\in(0,1)\) 时， \(f(x)>2\left(x+\dfrac{x^3}{2}\right)\) ；
• [(3)] 设实数 \(k\) 使得 \(f(x)>k\left(x+\dfrac{x^3}{2}\right)\) 对 \(x\in(0,1)\) 恒成立，求 \(k\) 的最大值。

问题：⁵¹ 已知函数 \(f(x)=\dfrac{x^2}{2}-k\ln x,\ k>0\) 。

• [(1)] 求 \(f(x)\) 的单调区间和极值；
• [(2)] 证明：若 \(f(x)\) 存在零点，则 \(f(x)\) 在区间 \((1,\sqrt{e}]\) 上仅有一个零点。

问题：⁵² 已知函数 \(f(x)=x\cos x-\sin x,\ x\in\left[0,\dfrac{\pi}{2}\right]\)

• [(1)] 求证：\(f(x)\leq0\)；
• [(2)] 证明：若 \(f(x)\) 存在零点，则 \(f(x)\) 在区间 \((1,\sqrt{e}]\) 上仅有一个零点。

问题：⁵³ 已知函数 \(f(x)=2x^3-3x\) 。

• [(1)] 求 \(f(x)\) 在区间 \([-2,1]\) 上的最大值；
• [(2)] 若过点 \(P(1,t)\) 存在三条直线与曲线 \(y=f(x)\) 相切，求 \(t\) 的取值范围；
• [(3)] 问过点 \(A(-1,2),\ B(2,10),\ C(0,2)\) 分别存在几条直线与曲线 \(y=f(x)\) 相切？（只需写出结论）

问题：⁵⁴ 设 \(L\) 为曲线 \(C:y=\dfrac{\ln x}{x}\) 在点 \((1,0)\) 处的切线。

• [(1)] 求 \(L\) 的方程；
• [(2)] 证明：除切点 \((1,0)\) 之外，曲线 \(C\) 在直线 \(L\) 的下方。

问题：⁵⁵ 已知函数 \(f(x)=x^2+x\sin x+\cos x\) 。

• [(1)] 求 \(L\) 的方程；
• [(2)] 证明：除切点 \((1,0)\) 之外，曲线 \(C\) 在直线 \(L\) 的下方。

问题：⁵⁶ 已知函数 \(f(x)=ax^2+1(a>0),g(x)=x^3+bx\) 。

• [(1)] 若曲线 \(y=f(x)\) 与曲线 \(y=g(x)\) 在它们的交点 \((1,c)\) 处具有公共切线，求 \(a,b\) 的值；
• [(2)] 当 \(a^2=4b\) 时，求函数 \(f(x)+g(x)\) 的单调区间，并求其在区间 \((-\infty,-1]\) 上的最大值。

问题：⁵⁷ 已知函数 \(f(x)=ax^2+1(a>0),g(x)=x^3+bx\) 。

• [(1)] 若曲线 \(y=f(x)\) 与曲线 \(y=g(x)\) 在它们的交点 \((1,c)\) 处具有公共切线，求 \(a,b\) 的值；
• [(2)] 当 \(a=3,b=-9\) 时，若函数 \(f(x)+g(x)\) 在区间 \([k,2]]\) 上的最大值为 \(28\) ，求 \(k\) 的取值范围。

问题：⁵⁸ 已知函数 \(f(x)=(x-k)^2\cdot e^{\frac{x}{k}}\)

• [(1)] 求 \(f(x)\) 的单调区间；
• [(2)] 若对于任意的 \(x\in(0,+\infty)\) 都有 \(f(x)\leq\dfrac{1}{e}\) ，求 \(k\) 的取值范围。

问题：⁵⁹ 已知函数 \(f(x)=(x-k)^2\cdot e^{\frac{x}{k}}\)

• [(1)] 求 \(f(x)\) 的单调区间；
• [(2)] 求 \(f(x)\) 在区间 \([0,1]\) 上的最小值。

问题：⁶⁰ 已知函数 \(f(x)=\ln(1+x)-x+\dfrac{k}{2}x^2(k\geq0)\)

• [(1)] 当 \(k=2\) 时，求曲线 \(y=f(x)\) 在点 \((1,f(x))\) 处的切线方程；
• [(2)] 求 \(f(x)\) 的单调区间。

问题：⁶¹ 设函数 \(f(x)=\dfrac{a}{3}x^3+bx^2+cx+d(a>0)\) ，且方程 \(f'(x)-9x=0\) 的两个根分别为 \(1,4\) 。

• [(1)] 当 \(a=3\) 且曲线 \(y=f(x)\) 过原点时，求 \(f(x)\) 的解析式；
• [(2)] 若 \(f(x)\) 在 \((-\infty,+\infty)\) 内无极值点，求 \(a\) 的取值范围。

问题：⁶² （未完待续）

问题：⁶³ 设函数 \(f(x)=a^2x^2+ax-3\ln x+1\)，其中\(a>0\) 。

1. 讨论 \(f(x)\) 的单调性；

2. 若 \(y=f(x)\) 的图像与 \(x\) 轴没有公共点，求 \(a\) 的取值范围。

问题：⁶⁴ 已知 \(a>0\) 且 \(a\neq1\) ，函数\(f(x)=\dfrac{x^a}{a^x}\ (x>0)\) 。

1. 当 \(a=2\) 时，求 \(f(x)\) 的单调区间。

2. 若曲线 \(y=f(x)\) 与直线 \(y=1\) 有且仅有两个交点，求 \(a\) 的取值范围。

问题：⁶⁵ 已知函数 \(f(x)=x^3-x^2+ax+1\)

1. 讨论 \(f(x)\) 的单调性；

2. 求曲线 \(y=f(x)\) 过坐标原点的切线与曲线 \(y=f(x)\) 的公共点的坐标。

问题：⁶⁶ 设函数 \(f(x)=\ln(a-x)\) ，已知 \(x=0\) 是函数 \(y=xf(x)\) 的极值点。

1. 求 \(a\) ；

2. 设函数 \(g(x)=\dfrac{x+f(x)}{xf(x)}\) ，证明：\(g(x)<1\) 。

问题：⁶⁷ 已知函数 \(f(x)=x(1-\ln x)\) 。

1. 讨论 \(f(x)\) 的单调性

2. 设 \(a,b\) 为两个不相等的正数，且 \(b\ln a-a\ln b=a-b\) ，

\(\qquad\) 证明： \(2<\dfrac{1}{a}+\dfrac{1}{b}<e\) 。

不等式（选做）真题汇编

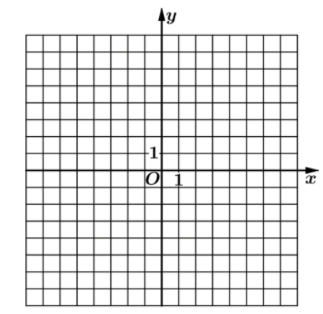
问题：⁶⁸⁶⁹ 函数 \(f(x)=|x-2|,\ g(x)=|2x+3|-|2x-1|\)

1. 画出 \(y=f(x)\) 和 \(y=g(x)\) 的图像；

2. 若 \(f(x+a)\geq g(x)\) ，求 \(a\) 的取值范围。

问题：⁷⁰⁷¹ 已知函数 \(f(x)=|x-a|+|x+3|\) 。

1. 当 \(a=1\) 时，求不等式 \(f(x)\geq6\) 的解集；

2. 若 \(f(x)>-a\) ，求 \(a\) 的取值范围。