组合、概率与统计

组合与概率

问题：¹ \(4\) 名同学到 \(3\) 个小区参加垃圾分类宣传活动，每名同学只去 \(1\) 个小区，每个小区至少安排 \(1\) 名同学，则不同的安排方法共有 \(\_\_\_\_\_\_\) 种。

问题：² 将一颗质地均匀的正方体骰子先后抛掷 \(2\) 次，观察向上的点数，则点数和为 \(5\) 的概率是 \(\_\_\_\_\_\_\)

问题：³ 设 \(O\) 为正方形 \(ABCD\) 的中心，在 \(O,A,B,C,D\) 中任取 \(3\) 点，则取到的 \(3\) 点共线的概率为

A. \(\dfrac{1}{5}\) \(\qquad\) B. \(\dfrac{2}{5}\) \(\qquad\) C. \(\dfrac{1}{2}\) \(\qquad\) D. \(\dfrac{4}{5}\)

问题：⁴ 在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成 \(1200\) 份订单的配货，由于订单量大幅增加，导致订单积压。为解决困难，许多志愿者踊跃报名参加配货工作。已知该超市某日积压 \(500\) 份订单未配货，预计第二天的新订单超过 \(1600\) 份的概率为 \(0.05\) ，志愿者每人每天能完成 \(50\) 份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于 \(0.95\)，则至少需要志愿者

A. \(10\) 名 \(\qquad\) B. \(18\) 名 \(\qquad\) C. \(24\) 名 \(\qquad\) D. \(32\) 名

问题：⁵ 从 \(6\) 人中选出 \(4\) 人去值班，每人值班一天，若第一天安排 \(1\) 人，第二天安排 \(1\) 人，第三天安排 \(2\) 人，则不同安排方法的种数为 \(\_\_\_\_\_\_\) （结果用数值表示）

问题：⁶ 已知甲、乙两球落入盒子的概率分别为 \(\dfrac{1}{2}\) 和 \(\dfrac{1}{3}\) ，假定两球是否落入盒子互不影响, 则甲、乙两球都落入盒子的概率为 \(\_\_\_\_\_\_\) ；甲、乙两球至少有一个 落入盒子的概率为 \(\_\_\_\_\_\_\)

问题：⁷ \(6\) 名同学到甲、乙、丙三个场馆做志愿者，每名同学只去 \(1\) 个场馆, 甲场馆安排 \(1\) 名，乙场馆安排 \(2\) 名，丙场馆安排 \(3\) 名，则不同的安排方法共有

A. \(120\) 种 \(\qquad\) B. \(90\) 种 \(\qquad\) C. \(60\) 种 \(\qquad\) D. \(30\) 种

问题：⁸ 要安排 3 名学生到 2 个乡村做志愿者, 每名学生只能选择去一个村, 每个 村里至少有一名志愿者, 则不同的安排方法共有

A. \(2\) 种 \(\qquad\) B. \(3\) 种 \(\qquad\) C. \(6\) 种 \(\qquad\) D. \(8\) 种

问题：⁹ 一个盒子里有 \(1\) 个红 \(1\) 个绿 \(2\) 个黄四个相同的球, 每次拿一个, 不放回, 拿出红球即停, 设拿出黄球的个数为 \(\xi\) ，则 \(P(\xi=0)=\_\_\_\_\_\_\) ，\(E(\xi)=\_\_\_\_\_\_\) 。

问题：¹⁰ 将 \(5\) 名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶 \(4\) 个项 目进行培训, 每名志愿者只分配到 \(1\) 个项目, 每个项目至少分配 \(1\) 名志愿者, 则不同的分配方案共有

A. \(60\) 种 \(\qquad\) B. \(120\) 种 \(\qquad\) C. \(240\) 种 \(\qquad\) D. \(480\) 种

问题：¹¹ 在区间 \((0,1)\) 和 \((1,2)\) 各随机取一个数，则两数之和大于 \(\dfrac{7}{4}\) 的概率为

A. \(\dfrac{7}{9}\) \(\qquad\) B. \(\dfrac{23}{32}\) \(\qquad\) C. \(\dfrac{9}{32}\) \(\qquad\) D. \(\dfrac{2}{9}\)

问题：¹² 在区间 \((0,1)\) 随机取一个数，则取到的数小于 \(\dfrac{1}{3}\) 的概率为

A. \(\dfrac{3}{4}\) \(\quad\) B. \(\dfrac{2}{3}\) \(\quad\) C. \(\dfrac{1}{3}\) \(\quad\) D. \(\dfrac{1}{6}\)

问题：¹³ 袋中有 \(4\) 个红球，\(m\) 个黄球， \(n\) 个绿球。现从中任取两个球，记取出的红球数为 \(\xi\)，若取出两个球都是红球的概率为 \(\dfrac{1}{6}\) ，一红一黄的概率为 \(1/3\) ，则 \(m-n=\_\_\_\_\_\_\) ，\(E(\xi)= \_\_\_\_\_\_\)

问题：¹⁴ 已知花博会有四个不同的场馆 \(A,B,C,D\) 。甲、乙两人每人选 \(2\) 个去参观，则他们的选择中恰有一个场馆相同的概率为 \(\_\_\_\_\_\_\)

问题：¹⁵ 有六个相同的球，分别标有数字 \(1,2,3,4,5,6\) ，从中有放回的随机取两次，每次取 \(1\) 个球。甲表示事件“第一次取出球的数字是 \(1\)”，乙表示事件“第一次取出球的数字是 \(2\)”，丙表示事件“两次取出球的数字之和是 \(8\)”，丁表示事件“两次取出球的数字之和是 \(7\)”，则 (    )

A. 甲与丙互相独立 \(\qquad\) B. 甲与丁互相独立

C. 乙与丙互相独立 \(\qquad\) D. 丙与丁互相独立

问题：¹⁶ 甲口袋中装有 \(2\) 个黑球和 \(1\) 个白球，乙口袋中装有 \(3\) 个白球。现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复 \(n\) 次这样的操作，记甲口袋中黑球个数为 \(X_n\) ，恰有 \(2\) 个黑球的概率为 \(p_n\) ，恰有 \(1\) 个黑球的概率为 \(q_n\) 。

1. 求 \(p_1, q_1\) 和 \(p_2, q_2\) ；

2. 求 \(2p_n+q_n\) 和 \(2p_{n-1}+q_{n-1}\) 的递推关系式和 \(X_n\) 的数学期望 \(E(X_n)\) （用 \(n\) 表示）。

问题：¹⁷ 甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束。经抽签，甲、乙首先比赛，丙轮空。设每场比赛双方获胜的概率都为 \(\dfrac{1}{2}\) 。

1. 求甲连胜四场的概率；

2. 求需要进行第五场比赛的概率；

3. 求丙最终获胜的概率。

问题：¹⁸ 某校为举办甲、乙两项不同活动，分别设计了相应的活动方案：方案一、方案二。为了解该校学生对活动方案是否支持，对学生进行简单随机抽样，获得数据如下表：

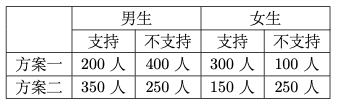
假设所有学生对活动方案是否支持相互独立。

1. 分别估计该校男生支持方案一的概率、该校女生支持方案一的概率；

2. 从该校全体男生中随机抽取 \(2\) 人, 全体女生中随机抽取 \(1\) 人，估计这 \(3\) 人中恰有 \(2\) 人支持方案一的概率；

3. 将该校学生支持方案二的概率估计值记为 \(p_0\) ，假设该校一年级有 \(500\) 名男生和 \(300\) 名女生，除一年级外其他年级学生支持方案二的概率估计值记为 \(p_1\) ，试比较 \(p_0\) 与 \(p_1\) 的大小。（结论不要求证明）

问题：¹⁹ 某学校组织“一带一路”知识竞赛, 有 A, B 两类问题。每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束；若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束。 \(A\) 类问题中的每个问题回答正确得 \(20\) 分, 否则得 \(0\) 分；\(B\) 类问题中的每个问题回答正确得 \(80\) 分，否则得 \(0\) 分。已知小明能正确回答 \(A\) 类问题的概率为 \(0.8\) ，能正确回答 \(B\) 类问题的概率为 \(0.6\) ，且能正确回答问题的概率与回答次序无关。

1. 若小明先回答 \(A\) 类问题，记 \(X\) 为小明的累计得分，求 \(X\) 的分布列；

2. 为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由。

统计量计算

问题：²⁰ 设一组样本数据 \(x_1,x_2,\cdots,x_n\) 的方差为 \(0.01\) ，则数据 \(10x_1,10x_2,\cdots,10x_n\) 的方差为

A. \(0.01\) \(\qquad\) B. \(0.1\) \(\qquad\) C. \(1\) \(\qquad\) D. \(10\)

问题：²¹ 在一组样本数据中， \(1,2,3,4\) 出现的频率分别为 \(p_1,p_2,p_3,p_4\) ，且 \(\sum\limits_{i=1}\limits^4p_i=1\) ，则下面四种情形中，对应样本的标准差最大的一组是

\(\quad\)A. \(p_1=p_4=0.1,p_2=p_3=0.4\)

\(\quad\)B. \(p_1=p_4=0.4,p_2=p_3=0.1\)

\(\quad\)C. \(p_1=p_4=0.2,p_2=p_3=0.3\)

\(\quad\)D. \(p_1=p_4=0.3,p_2=p_3=0.2\)

问题：²² 设 \(a,b\in\mathbb{R}\)，若 \(1,2,a,b\) 这四个数的中位数为 \(3\) ，平均数为 \(4\) ，则 \(ab=\_\_\_\_\_\_\) 。

问题：²³ 有一组样本数据 \(x_1,x_2,\cdots,x_n\) ，由这组数据得到的新样本数据 \(y_1,y_2,\cdots,y_n\) ，其中 \(y_i=x_i+c (i=1,2,\cdots,n)\) ，\(c\) 为非零常数，则 (    ) （多选题）

\(\quad\)A. 两组样本数据的样本平均数相同

\(\quad\)B. 两组样本数据的样本中位数相同

\(\quad\)C. 两组样本数据的样本标准差相同

\(\quad\)D. 两组样本数据的样本极差相同

问题：²⁴ 某厂接受了一项加工业务，加工出来的产品（单位: 件）按标准分为 \(A, B, C, D\) 四个等级。加工业务约定：对于 \(A\) 级品、 \(B\) 级品、 \(C\) 级品，厂家每件分别收取加工费 \(90\) 元， \(50\) 元， \(20\) 元；对于 \(D\) 级品，厂家每件要赔偿原料损失费 \(50\) 元。该厂有甲、乙两个分厂可承接加工业务。甲分厂加工成本费 为 \(25\) 元/件，乙分厂加工成本费为 \(20\) 元/件。厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了 \(100\) 件这种产品，并统计了这些产品的等级，整理如下：

\(\quad\)(1) 分别估计甲、乙两分厂加工出来的一件产品为 \(A\) 级品的概率；

\(\quad\)(2) 分别求甲、乙两分厂加工出来的 \(100\) 件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务？

问题：²⁵ 某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加。为调查该地区某种野生动物的数量，将其分成面积相近的 \(200\) 个地块，从这些地块中用简单随机抽样的方法抽取 \(20\) 个作为样区，调查得到样本数据 \((xi,yi) (i = 1, 2, ··· , 20)\) ，其中 \(x_i\) 和 \(y_i\) 分别表示第 \(i\) 个样区的植物覆盖面积（单位：公顷）和这种野生动物的数量，并计算得 \(\sum\limits_{i=1}\limits^{20}x_i=60,\sum\limits_{i=1}\limits^{20}y_i=1200,\sum\limits_{i=1}\limits^{20}(x_i-\bar{x})^2=80,\sum\limits_{i=1}\limits^{20}(y_i-\bar{y})^2=9000,\sum\limits_{i=1}\limits^{20}(x_i-\bar{x})(y_i-\bar{y})=800\)

\(\quad\)(1) 求该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数）；

\(\quad\)(2) 求样本 \((x_i,y_i) (i = 1, 2, ··· , 20)\) 的相关系数（精确到 \(0.01\) ）；

\(\quad\)(3) 根据现有统计资料，各地块间植物覆盖面积差异很大。为提高样本的代表性以获得该地区这种野生动物数量更准确的估计，请给出一种你认为更合理的抽样方法。并说明理由。

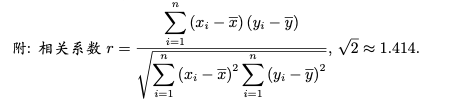
图表阅读

问题：²⁶ 某校一个课外学习小组为研究某作物种子的发芽率 \(y\) 和温度 \(x\) （单位: \(\circ C\)） 的关系，在 \(20\) 个不同的温度条件下进行种子发芽实验，由实验数据 \((x_i, y_i) (i = 1, 2, ··· , 20)\) 得到下面的散点图：

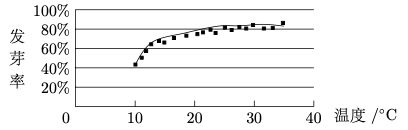
由此散点图，在 \(10\circ C\)至 \(40\circ C\) 之间，下面四个回归方程类型中最适宜作为发芽率 \(y\) 和温度 \(x\) 的回归方程类型的是：

A. \(y=a+bx\) \(\qquad\) B. \(y=a+bx^2\)

C. \(y=a+be^x\) \(\qquad\) D. \(y=a+b\ln x\)

问题：²⁷ 从一批零件中抽取 \(80\) 个, 测量其直径 (单位: \(mm\)), 将所得数据分为 \(9\) 组: \([5.31,5.33), [5.33,5.35), \cdots, [5.45,5.47), [5.47,5.49]\), 并整理得到如下 频率分布直方图, 则在被抽取的零件中, 直径落在区间 [5.43, 5.47) 内的个数为

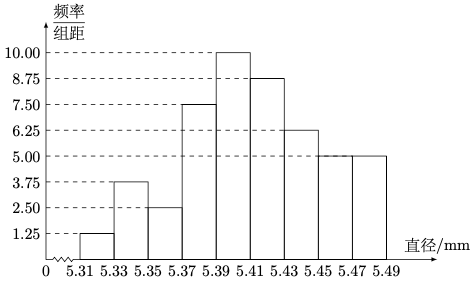
A. \(10\) \(\qquad\) B. \(18\) \(\qquad\) C. \(20\) \(\qquad\) D. \(36\)

问题：²⁸ 我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续 \(11\) 天复工复产指数折线图，下列说法正确的是

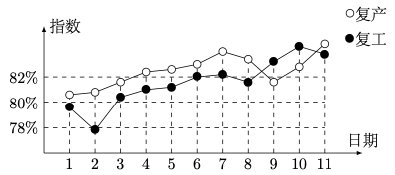
\(\quad\)(A) 这 \(11\) 天复工指数和复产指数均逐日增加

\(\quad\)(B) 这 \(11\) 天期间，复产指数增量大于复工指数的增量

\(\quad\)(C) 第 \(3\) 天至第 \(11\) 天复工复产指数均超过 \(80\%\)

\(\quad\)(D) 第 \(9\) 天至第 \(11\) 天复产指数增量大于复工指数的增量

问题：²⁹ 为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：

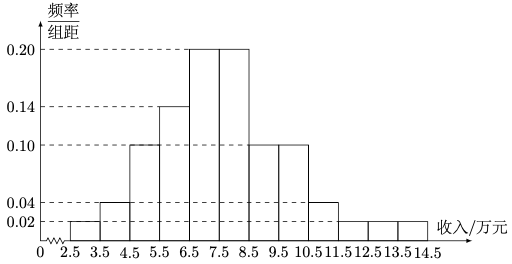
根据此频率分布直方图，下面结论中不正确的是 (    )

\(\quad\)(A) 该地农户家庭年收入低于 \(4.5\) 万元的农户比率估计为 \(6\%\)

\(\quad\)(B) 该地农户家庭年收入不低于 \(10.5\) 万元的农户比率估计为 \(10\%\)

\(\quad\)(C) 估计该地农户家庭年收入的平均值不超过 \(6.5\) 万元

\(\quad\)(D) 估计该地有一半以上的农户, 其家庭年收入介于 \(4.5\) 万元至 \(8.5\) 万元之间

显著性检验

问题：³⁰ 某学生兴趣小组随机调查了某市 \(100\) 天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表 (单位：天)：

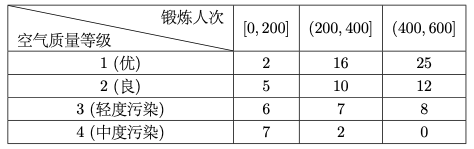
\(\quad\)(1) 分别估计该市一天的空气质量等级为 \(1, 2, 3, 4\) 的概率；

\(\quad\)(2) 求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组 区间的中点值为代表）；

\(\quad\)(3) 若某天的空气质量等级为 \(1\) 或 \(2\) ，则称这天“空气质量好”；若某天的空气质量等级为 \(3\) 或 \(4\) ，则称这天“空气质量不好”。根据所给数据，完成下面 的 \(2 × 2\) 列联表，并根据列联表，判断是否有 \(95\%\) 的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？

问题：³¹ 为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了 \(100\) 天空气中的 \(PM2.5\) 和 \(SO2\) 浓度 (单位: \(\mu g/m^3\)), 得下表：

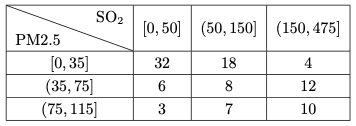
\(\quad\)(1) 估计事件“该市一天空气中 \(PM2.5\) 浓度不超过 \(75\) ，且 \(SO2\) 浓度不超过 \(150\)”的概率；

\(\quad\)(2) 根据所给数据, 完成下面的 \(2 × 2\) 列联表：

\(\quad\)(3) 根据 (2) 中的列联表，判断是否有 \(99\%\) 的把握认为该市一天空气中 \(PM2.5\) 的浓度与 \(SO2\) 浓度有关？

问题：³² 甲、乙两台机床生产同种产品，产品质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了 \(200\) 件产品, 产品的质量情况统计如下表：

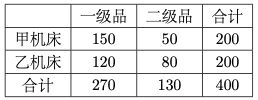
\(\quad\)(1) 甲机床、乙机床生产的产品中一级品的频率分别是多少？

\(\quad\)(2) 能否有 \(99\%\) 的把握认为甲机床的产品质量与乙机床的产品质量有差异？

问题：³³ 某厂研制了一种生产高精产品的设备，为检验新设备生产产品的某项指标有无提高，用一台旧设备和一台新设备各生产了 \(10\) 件产品，得到各件产品该项指标数据如下。旧设备和新设备生产产品的该项指标的样本平均值分别记为 \(\bar{x}\) 和 \(\bar{y}\) ，样本方差分別记为 \(s_1^2\) 和 \(s_2^2\)。

\(\quad\)(1) 求 \(\bar{x}\) ，\(\bar{y}\) ，\(s_1^2\) 和 \(s_2^2\)。

\(\quad\)(2) 判断新设备生产产品的该项指标的均值较旧设备是否有显著提高（如果 \(\bar{y}-\bar{x}\geq2\sqrt{\dfrac{s_1^2+s_2^2}{10}}\) ，则认为新设备生产产品的该项指标的均值较旧设 备有显著提高, 否则不认为有显著提高）。