函数基础练习-I

函数变换基础练习

示例： 写出变量代换后的的函数解析式（展开形式）：

1. \(f(x)=2x+1\) ，则 \(f(2x+1)=\)

2. \(f(x)=3-2x\) ，则 \(f(1-x)=\)

3. \(f(t)=t^2+t\) ，则 \(f(1-m)=\)

4. \(g(m)=3-m^2\) ，则 \(g(m-n)=\)

示例： 写出复合后的函数解析式（展开形式）：

1. \(f(x)=3x+2,\ g(x)=2x+1\) ，则 \(f(g(t))=\)

2. \(f(x)=x-2,\ g(x)=2x^2+1\) ，则 \(g(f(t)+1)=\)

3. \(f(t)=2t+k,\ g(x)=3x-1\) ，则 \(g(2f(x))=\)

4. \(f(t)=2t+1\) ，则 \(f(f(f(x)))=\)

示例： 写出变量代换前的函数解析式：

1. \(f(2x+1)=4x+5\) ，则 \(f(x)=\)

2. \(f(1-2x)=4x+5\) ，则 \(f(x)=\)

3. \(f(t+1)=t^2+2t+3\) ，则 \(f(x)=\)

4. \(f(t+1)=t^2+t+3\) ，则 \(f(x)=\)

示例： 写出复合函数的母函数解析式

1. \(f(g(x))=2x+5,\ g(x)=2x\) ，则 \(f(x)=\)

2. \(f(g(x))=2x+5,\ f(x)=2x\) ，则 \(g(x)=\)

3. \(f(g(x))=x^2+2x,\ f(x)=x^2\) ，则 \(g(x)=\)

4. \(f(g(x))=x^2+3x+2,\ f(x)=(1-x)^2\) ，则 \(g(x)=\)

示例： 写出变换后的函数解析式：

1. \(f(x)=\dfrac{1}{x}\) ，则 \(f(x+1)+1=\dfrac{x+2}{x+1}\)

2. \(f(x)=\dfrac{1}{x}\) ，则 \(f(2-3x)-2=\)

3. \(f(x)=\dfrac{2}{x}\) ，则 \(f(1-x)+1=\)

4. \(f(x)=\dfrac{k}{x}\) ，则 \(f(x+m)-n=\)

示例： 写出复合函数的母函数解析式：

1. \(f(x)=\dfrac{1+x}{x},\ f(g(x))=\dfrac{x}{x-1}\) ，则 \(g(x)=\)

2. \(f(x)=\dfrac{x}{1-x},\ f(g(x))=\dfrac{3-x}{x-2}\) ，则 \(g(x)=\)

3. \(f(x)=\dfrac{1+x}{1-x},\ f(g(x))=x\) ，则 \(g(x)=\)

4. \(f(x)=\dfrac{1+x}{1-x},\ f(g(x))=\dfrac{1}{x}\) ，则 \(g(x)=\)

示例： 写出复合函数的母函数解析式：

1. \(g(x)=x+1,\ f(g(x))=x^2+1\) ，则 \(f(x)=\)

2. \(g(x)=2x+1,\ f(g(x))=x^2+1\) ，则 \(f(x)=\)

3. \(g(x)=x+1,\ f(g(x))=\dfrac{1+x}{1-x}\) ，则 \(f(x)=\)

4. \(g(x)=\dfrac{1-x}{1+x},\ f(g(x))=x\) ，则 \(f(x)=\)

示例： 写出复合后的函数解析式：

1. \(f(x)=x+\dfrac{1}{x},\ g(x)=x+1\) ，则 \(f(g(x))=\dfrac{x^2+2x+2}{x+1}\)

2. \(f(x)=x+\dfrac{1}{x},\ g(x)=x^2+1\) ，则 \(f(g(x))=\)

3. \(f(x)=x+\dfrac{1}{x},\ g(x)=2-x\) ，则 \(f(g(x))=\)

4. \(f(x)=x+\dfrac{1}{x},\ g(x)=\dfrac{x+1}{x-1}\) ，则 \(f(g(x))=\)

示例： 写出复合函数的母函数解析式：

1. \(f(g(x))=x^3+\dfrac{1}{x^3},\ g(x)=x+\dfrac{1}{x}\) ，则 \(f(x)=\)

2. \(f(g(x))=\dfrac{x^3+x}{x^4+x^2+1},\ g(x)=x+\dfrac{1}{x}\) ，则 \(f(x)=\)

3. \(f(g(x))=\dfrac{1}{x^2}(2x^4+3x^3+5x^2+3x+2),\ g(x)=x+\dfrac{1}{x}\) ，则 \(f(x)=\)

4. \(f(g(x))=\dfrac{1}{x^2}(2x^4+3x^3+5x^2-3x+2),\ g(x)=x-\dfrac{1}{x}\) ，则 \(f(x)=\)

示例： 将 \(f(x)\) 变形为 \(g(x)+\dfrac{k}{g(x)}+b\) 的形式：

1. \(f(x)=\dfrac{x^2+1}{x}=\)(2) \(f(x)2x+\dfrac{2}{x}=\)

2. \(f(x)=\dfrac{2x^2+1}{x}=\)(4) \(f(x)=\dfrac{2x^2-3x+3}{x-1}=\)

示例： 求函数 \(f(x)\) 的解析式

1. \(2f(x)+f(\dfrac{1}{x})=x\) ，则 \(f(x)=\)

2. \(2f(x)+f(1-x)=x\) ，则 \(f(x)=\)

3. \(2f(x)+f(\sqrt{1-x^2})=x,\ x\in[0,1]\) ，则 \(f(x)=\)

示例： 写出复合后的函数解析式：

1. \(f(x)=e^x,\ g(x)=\ln x\) ，则 \(f(g(x))=\)

2. \(f(x)=xe^x,\ g(x)=\ln x\) ，则 \(f(g(x))=\)

3. \(f(x)=\ln x,\ g(x)=e^{x}\) ，则 \(f(g(x))=\)

4. \(f(x)=\ln x,\ g(x)=xe^x\) ，则 \(f(g(x))=\)

示例： 写出复合函数的母函数解析式：

1. \(f(g(x))=\dfrac{e^x}{e},\ f(x)=e^x\) ，则 \(g(x)=\)

2. \(f(g(x))=e^x,\ g(x)=x-1\) ，则 \(f(x)=\)

3. \(f(g(x))=e^{x+\ln 2-1},\ f(x)=2x\) ，则 \(g(x)=\)

4. \(f(g(x))=e^{x+\ln 2-1},\ g(x)=e^x\) ，则 \(f(x)=\)

示例： 已知 \(y=f(x),\ x\in\mathbb{R}\) ，根据要求写出函数（或方程）解析式：

1. 图像与 \(y=f(x)\) 关于 \(x=1\) 成轴对称：

2. 图像与 \(y=f(x)\) 关于 \(y=1\) 成轴对称：

3. 图像与 \(y=f(x)\) 关于 \(x=y\) 成轴对称：

4. 图像与 \(y=f(x)\) 关于 \(x=-y\) 成轴对称：

示例： 已知 \(y=f(x),\ x\in\mathbb{R}\) ，根据要求写出函数（或方程）解析式：

1. 图像与 \(y=f(x)\) 关于点 \((0,1)\) 成中心对称：

2. 图像与 \(y=f(x)\) 关于点 \((1,0)\) 成中心对称：

3. 图像与 \(y=f(x)\) 关于点 \((1,1)\) 成中心对称：

4. 图像与 \(y=f(x)\) 关于点 \((a,b)\) 成中心对称：

示例： 根据已知条件，分析函数的对称性：

1. \(f(x)=f(1+x)\) ：(2) \(f(x)=f(1-x)\) ：

2. \(f(-x)=f(1+x)\) ：(4) \(f(-x)=f(1-x)\) ：

示例： 探究函数的周期性并证明。

1. \(f(x)\) 是偶函数，图像关于 \(x=1\) 对称；

2. \(f(x)\) 是偶函数，图像关于 \((1,0)\) 中心对称；

3. \(f(x)\) 是奇函数，图像关于 \(x=1\) 对称；

4. \(f(x)\) 是奇函数，图像关于 \((1,0)\) 中心对称；

示例： \(f(x)=\sin(\omega x+\phi)\) ，依据要求确定函数的参数，并绘制图像。

1. \(f(x)\) 是偶函数，图像关于 \(x=1\) 对称；

2. \(f(x)\) 是偶函数，图像关于 \((1,0)\) 中心对称；

3. \(f(x)\) 是奇函数，图像关于 \(x=1\) 对称；

4. \(f(x)\) 是奇函数，图像关于 \((1,0)\) 中心对称；

示例： \(f(x)=\cos(\omega x+\phi)\) ，依据要求确定函数的参数，并绘制图像。

1. \(f(x)\) 是偶函数，图像关于 \(x=1\) 对称；

2. \(f(x)\) 是偶函数，图像关于 \((1,0)\) 中心对称；

3. \(f(x)\) 是奇函数，图像关于 \(x=1\) 对称；

4. \(f(x)\) 是奇函数，图像关于 \((1,0)\) 中心对称；

示例： \(f(x)\) 是偶函数，周期为 \(2\) ，\(f(0.5)=2\) 。

示例： \(f(x)\) 是奇函数，周期为 \(2\) ，\(f(0.5)=2\) 。

示例： \(f(x)\) 是奇函数，且 \(f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

示例： \(f(x)\) 是偶函数，且 \(f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

示例： \(f(x)\) 是奇函数，且 \(-f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

示例： \(f(x)\) 是偶函数，且 \(-f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

定义域和值域

示例： 求下列函数的定义域和值域。

1. \(f(x)=\dfrac{1}{x-|x|}\)

2. \(f(x)=\dfrac{1}{1+\dfrac{1}{x}}\)

3. \(f(x)=\sqrt{-x^2-4x+5}\)

4. \(f(x)=\sqrt{x^2-6x+10}\)

示例： \(\bigstar\)求下列函数的定义域和值域。

1. \(f(x)=\dfrac{\sqrt{4-x^2}}{x-1}\)

2. \(f(x)=\sqrt{1-x}+\sqrt{x+3}-1\)

示例： 已知 \(f(x)=\begin{cases}x+2(x\leq-1)\\x^2\ (-1<x<2)\\2x\ (x\geq2)\end{cases}\) ，若 \(f(a)=3\) ，求 \(a\)

示例： 若函数 \(y=\dfrac{ax-1}{\sqrt{ax^2+4ax+3}}\) 的定义域为 \(\mathbb{R}\) ，求 \(a\) 的取值范围。

示例： 已知函数 \(y=\dfrac{2x-1}{x-1}\) 的值域是 \(\{y|y\leq0\}\cup\{y|y\geq3\}\) ，求此函数的定义域。

示例： 已知 \(f(x+1)\) 的定义域为 \([-2,3)\) ，求 \(f(\dfrac{1}{x}+2)\) 的定义域。

示例： 已知扇形的周长为 \(10\) ，求扇形半径 \(r\) 和面积 \(s\) 的函数关系式 \(s(r)\) ，及此函数的定义域和值域。

示例： 已知函数 \(y=f(x)\) 的定义域为 \((0,1]\) ，求 \(y=f(x^2)+f(x+1)\) 的定义域。

示例： 求函数 \(y=2x-\sqrt{x-1}\) 的值域。

示例： 已知函数 \(f(x)=|x-1|+|x-3|\)

1. 求函数 \(f(x)\) 的值域。

2. 若不等式 \(f(x)\geq a\) 对于一切实数都成立，求 \(a\) 的值。

示例： 已知 \(f(x-1)=|x|-|x-2|\) ，\(f(m)=f(2008)-\dfrac{7}{2}\) ，则 \(m\) 的值为：

A. \(-\dfrac{3}{4}\)B. \(-\dfrac{3}{2}\)C. \(-2\)D. \(2\)

单调性

示例： 判定函数 \(f(x)=\dfrac{ax}{x^2-1}\ (x\in(-1,1))\) 的单调性。

示例： 讨论函数 \(f(x)=x^2-2|x|-3\) 的单调区间。

示例： 讨论函数 \(f(x)=-x^2+2|x|-3\) 的单调区间。

示例： 讨论函数 \(f(x)=|x^2-2x-3|\) 的单调区间。

示例： 讨论函数 \(y=|x|\cdot(1-x)\) 的单调区间。

示例： 已知函数 \(f(x)\) 为 \(\mathbb{R}\) 上的减函数，则满足 \(f\left(\left|\dfrac{1}{x}\right|\right)<f(1)\) 的实数 \(x\) 的取值范围是

A. \((-1,1)\)B. \((0,1)\)C. \((-1,0)\cup(0,1)\)D. \((-\infty,-1)\cup(1,\infty)\)

示例： 设函数定义在 \(\mathbb{R}\) 上，对于任意实数 \(m,n\) 恒有 \(f(m+n)=f(m)f(n)\) ，当 \(x>0\) 时， \(0<f(x)<1\)

• [(1)] 求证：\(f(0)=1\) 且当 \(x<0\) 时， \(f(x)>1\) ；
• [(2)] 求证：\(f(x)\) 在 \(\mathbb{R}\) 上单调递减；
• [(3)] 设集合 \(A=\{(x,y)|f(x^2)f(y^2)=f(1)\},\ B=\{(x,y)|f(ax-y+2)=1,a\in\mathbb{R}\}\) ，若 \(A\cap B=\Phi\) ，求 \(a\) 的取值范围。

示例： 已知函数 \(f(x)=\dfrac{a+bx}{a-bx},\ x\in[-1,1]\) 。

1. \(a=1, b=3\) 时，证明 \(f(x)\) 在 \([-1,0]\) 上是增函数；

2. \(a>b>0\) 时，证明 \(f(x)\) 在 \([-1,1]\) 上是增函数；

3. 求函数 \(f(x)\) 的值域。

示例： (1) 证明函数 \(f(x)=\dfrac{x}{1+x^2}\) 在 \((-1,1)\) 上是增函数。

2. 讨论函数 \(f(x)=\dfrac{kx}{1+x^2}\) 在 \((-1,1)\) 上的单调性。

示例： 已知函数 \(f(x)=x^2-2ax+a^2-1\)

1. 若函数 \(f(x)\) 在区间 \([0,2]\) 上是单调的，求实数 \(a\) 的取值范围；

2. 当 \(x\in[-1,1]\) 时，求函数 \(f(x)\) 的最小值 \(g(a)\) ，并画出最小值函数 \(y=g(a)\) 的图像。

函数的奇偶性

示例： 判断下列函数的奇偶性：

1. \(y=2x+\sqrt[3]{x}\)

2. \(y=|x+1|+|x-1|\)

3. \(y=x^2+x+1\)

4. \(f(x)=\begin{cases}x^2+2x-1\ &(x>0)\\0&(x=0)\\-x^2+2x+1\ &(x<0)\end{cases}\)

5. \(f(x)=\sqrt{1-x^2}+\sqrt{x^2+1}\)

6. \(\bigstar\ f(x)=\dfrac{\sqrt{1-x^2}}{|x+2|-2}\)

示例： 已知偶函数 \(f(x)\) 在区间 \([0,4]\) 上是增函数，试比较 \(f(-3)\) 与 \(f(\pi)\) 的大小。

示例： 若奇函数 \(f(x)\) 在 \([3,7]\) 上的最小值是 \(5\) ，那么 \(f(x)\) 在 \([-7,-3]\) 上：

A. 最小值是 \(5\) B. 最小值是 \(-5\)

C. 最大值是 \(-5\) D. 最大值是 \(5\)

示例： \(f(x)\) 是定义在 \(\mathbb{R}\) 上的奇函数，又 \(f(x)\) 在区间 \((0,+\infty)\)上是增函数，且 \(f(1)=0\) ，则满足 \(f(x)>0\) 的 \(x\) 的取值集合是 \(\_\_\_\_\_\_\)

示例： 设 \(f(x)\) 是 \((-\infty,+\infty)\) 上的奇函数， \(f(x+2)=-f(x)\), 当 \(0\leq x\leq1\)时，\(f(x)=x\) ,则 \(f(7.5)\) 等于：

A. \(0.5\)B. \(-0.5\)C. \(1.5\)D. \(-1.5\)

示例： 如果函数 \(f(x)\) 在 \(R\) 上为奇函数，在 \([-1,0)\) 上是增函数，且 \(f(x+2)=-f(x)\) , 试比较 \(f(\dfrac{1}{3}),\ f(\dfrac{2}{3}),\ f(1)\) 的大小关系 \(\_\_\_\_\_\_\_\_\_\)

示例： 若 \(f ( x)\) 为奇函数，且在 \((0, +\infty )\) 内是增函数，又 \(f(-3)=0\) ，则 \(xf(x)<0\) 的解集为 \(\_\_\_\_\_\_\)

示例： 设奇函数 \(f (x)\) 的定义域为 \([-5,5]\)，若当 \(x\in[0,5]\) 时, \(f (x)\) 的图象 如右图，则不等式 \(f(x)<0\) 的解是 \(\_\_\_\_\_\_\)

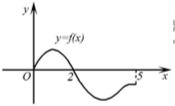
示例： 已知 \(f(x)\) 是定义在 \(\mathbb{R}\) 上的奇函数，当 \(x≥0\) 时， \(f(x)=x^2-2x\) ，则 \(f(x)\) 在 \(\mathbb{R}\) 上的表达式是

A. \(f(x)=x^2-2x\)B. \(f(x)=x(|x|-1)\)

C. \(f(x)=|x|(x-2)\)D. \(f(x)=x(|x|-2)\)

示例： 函数 \(f(x)\) 是定义在 \([-6,6]\) 上的偶函数，且在 \([-6,0]\) 上是减函数，则

A. \(f(3)+f(4)>0\)B. \(f(-3)-f(2)<0\)

C. \(f(-2)+f(-5)<0\)D. \(f(4)-f(-1)>0\)

示例： 设 \(f(x)\) 是定义在 \(\mathbb{R}\) 上的任意一个增函数，令 \(F(x)= f(x)-f(-x)\)，则 \(F(x)\) 必是

A. 增函数且是奇函数B. 增函数且是偶函数

C. 减函数且是奇函数D. 减函数且是偶函数

示例： 设 \(f(x),g(x)\) 都是奇函数， \(F(x)=f(x)+g(x)+3\) ，若 \(F(5)=9\) ，则 \(F(-5)=\)

A. \(3\) B. \(-3\) C. \(-6\) D. \(-9\)

示例： 设 \(f(x),\ g(x)\) 都是奇函数，且 \(F(x)=af(x)+bg(x)+2\) ，若在 \((0, +\infty)\) 上 \(F(x)\) 有最大值 \(8\)，则在 \((-\infty, 0)\) 上 \(F(x)\) 有

A. 最小值 \(-8\)B. 最大值 \(-8\)C. 最小值 \(-4\)D. 最小值 \(-6\)

示例： 函数 \(f(x)=\dfrac{\sqrt{1-x^2}}{|x+3|-3}\) 是

A. 奇函数B. 偶函数C. 既奇又偶函数D. 无确定奇偶性

示例： 若 \(f(x)=ax^2+bx+c\ (a\neq0)\) 是偶函数，则 \(g(x)=ax^3+bx^2+cx\) 是

A. 奇函数B. 偶函数C. 既奇又偶函数D. 无确定奇偶性

示例： 下列命题中真命题个数是

1. 偶函数图象一定与 \(y\) 轴相交

2. 奇函数图象一定过原点

3. 偶函数图象关于 \(y\) 轴对称

4. 既奇又偶函数一定满足 \(f ( x) = 0\)

A. \(1\) B. \(2\)C. \(3\)D. \(4\)

示例： 若奇函数 \(f (x)\) 在区间 \([3,7]\) 上是增函数，且最小值为 \(5\) ，那么在区间 \([-7,-3]\) 上是( )

A. 增函数且最小值为 \(-5\) B. 增函数且最大值为 \(-5\)

C. 减函数且最小值为 \(-5\) D. 减函数且最大值为 \(-5\)

示例： 下列四个命题中正确的个数是

1. \(f(x)=1\) 是偶函数;

2. \(g(x)=x^3, x\in (-1,1]\) 是奇函数;

3. 若 \(f(x)\) 是奇函数，\(g(x)\)是偶函数，则 \(H(x)= f(x)\cdot g(x)\)一定是奇函数;

4. 函数 \(y=f(x)\) 的图象关于 \(y\) 轴对称。

A. \(1\)B. \(2\)C. \(3\)D. \(4\)

示例： 已知\(f(x)=x^4+ax^3+bx-8\)，且 \(f(-2)=10\)，则\(f(2)=\)

示例： 判断下列函数的奇偶性:

1. \(\begin{cases} x+1\ &(x>0)\\1 &(x=0)\\-x+1&(x<0) \end{cases}\)

2. \(f(x)\) 不恒为 \(0\) ，且对 \(a,b\in\mathbb{R}\) 恒有 \(f(a+b)=f(a)+f(b)\)

示例： 已知 \(f(x)\) 是定义在 \(\mathbb{R}\) 上的奇函数，当 \(x>0\) 时, \(f(x)=\sqrt{x}+1\) ，则 $f (x) = $

示例： 函数 \(f(x)\) 的定义域为 \(\mathbb{R}\) ，若 \(f(x+1)\) 与 \(f(x-1)\) 都是奇函数，则：

A. \(f(x)\) 是偶函数 B. \(f(x)\) 是奇函数

C. \(f(x)=f(x+2)\)D. \(f(x+3)\) 是奇函数

示例： 是否存在常数\(m,n\)，使函数 \(f(x)=(m^2-1)x^2+(m-1)x+n+2\) 为奇函数？

示例： 已知 \(f(x),g(x)\) 均为奇函数，且定义域相同。

求证： \(f(x)+g(x)\) 为奇函数， \(f(x)\cdot g(x)\) 为偶函数。

示例： 设函数 \(y= f(x)\) 对于任意的 \(x,y\in R\) 都有 \(f(x+y)= f(x)+ f(y)\) ，且 \(f(x)\) 不恒为零，判断 \(f(x)\) 的奇偶性。

示例： 已知函数 \(f(x)\) 满足 \(f(x+y)+f(x-y)=2f(x)\cdot f(y)\ (x,y\in\mathbb{R})\) ，且 \(f(0)\neq0\) ，判定函数 \(f(x)\) 的奇偶性并证明。

示例： 已知函数 \(y=f(x)\) 为奇函数，在 \((0,+\infty)\) 内是减函数，且 \(f(x)<0\) ，试问：\(F(x)=\dfrac{1}{f(x)}\) 在 \((-\infty,0)\) 内增减性如何？并证明之。

示例： 已知偶函数 \(f(x)\) 的定义域时 \(\mathbb{R}\) ，当 \(x<0\) ， \(f(x)=x^2-3x-1\) ，求 \(f(x)\) 的解析式。

示例： 已知奇函数 \(f(x)\) 的定义域时 \(\mathbb{R}\) ，当 \(x>0\) ， \(f(x)=x^2+2x-1\) ，求 \(g(x)\) 的解析式。

示例：

1. \(f(x)\) 是定义在 \(\mathbb{R}\) 上的偶函数，且当 \(x\leq0\) 时，\(f(x)=x^2-x\)，求 \(f(x)\) 的解析式.并画出函数图象，求出函数的值域;

2. 已知 \(f(x)\) 是定义在R上的奇函数，当 \(x>0\) 时 \(f(x)=x^2-4x+3\) ，求 \(f(x)\) 的解析式.

示例： 已知函数 \(f (x)\)是定义在区间 \([-2,2]\) 上的偶函数，当 \(x\in[0,2]\)时， \(f (x)\)是减函数，如果不等式 \(f(1-m)<f(m)\) 成立，求实数 \(m\) 的取值范围。

示例： 已知函数 \(f(x)\) 定义域 \(\mathbb{R}\) ，为对任意的 \(x1,x2\in\mathbb{R}\) 都有 \(f(x1 +x2)= f(x1)+ f(x2)\) 且 \(x>0\) 时 \(f (x)<0,\ f(1)=-2\)，试判断在区间 \([-3,3]\) 上 \(f(x)\) 是否有最大值和最小值？如果有试求出最大值和最小值，如果没有请说明理由。

示例： 已知函数 \(f(x)\) 定义域 \(\mathbb{R}\) ,为对任意的 \(x1,x2\in\mathbb{R}\) 都有 \(f(x1 +x2)= f(x1)f(x2)\) 且 \(x>0\) 时 \(0<f (x)<1\) ，求 \(f(0)\) 的值并求 \(x<0\) 时 \(f(x)\) 的取值范围。

反函数

示例： 函数 \(y=\sqrt{-x},\ (x\leq0)\) 的反函数是：

A. \(y=x^2\ (x\geq0)\)B. \(y=-x^2\ (x\geq0)\)

C. \(y=x^2\ (x\leq0)\)B. \(y=-x^2\ (x\leq0)\)

示例： 已知 \(y=x|x|+2x\) ，求 \(f^{-1}(x)\)

示例： 设 \(P(1,2)\) 在 \(f(x)=ax^2+b,\ (x\geq0)\) 的图像上，又在它的反函数图像上，求 \(f^{-1}(x)\) 。

综合问题

示例： 已知 \(y=f(x)\) 表示过点 \((0,-2)\) 的直线， \(y=g(x)\) 表示过点 \((0,0)\) 的直线，又 \(f(g(x))=g(f(x))=3x-2\) ，求两直线交点坐标。

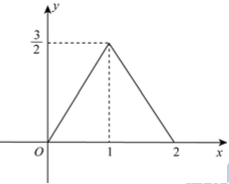
示例： 写出图 2 所示函数的定义，要求使用绝对值记法而非分段函数。

示例： 已知 \(f(\dfrac{x+1}{x})=\dfrac{x^2+1}{x^2}+\dfrac{1}{x}\) ，求 \(f(x)\) 。

示例： 已知 \(2f(x^2)+f(\dfrac{1}{x^2})=x\ (x>0)\) ，求 \(f(x)\)

示例： 定义 \(f_n(x)\) ：\(n=1\) 时 \(f_1(x)=f(x)\) ； \(n\) 为大于 \(1\) 的自然数时 \(f_n(x)=f(f_{n-1}(x))\) 。

若 \(f(x)=\dfrac{x}{\sqrt{1-x^2}}\) ，求 \(f_n(x)\) 。

示例： 已知，定义在 \(\mathbb{R}\) 上的函数 \(f(x)\) 是以 \(2\) 为周期的函数，且当 \(x\in[0,2]\) 时， \(f(x)=|x+1|\) ，求 \(x\in\mathbb{R}\) 时， \(f(x)\) 的解析式。

示例： 求 \(f(x)=x-\sqrt{1-2x}\) 的值域。

示例： 求 \(f(x)=\dfrac{a+bx}{a-bx}\ (a>b>0),\ x\in[-1,1]\) 的值域。

示例： 求 \(f(x)=\dfrac{x^2-x+1}{x^2+x+1}\) 的值域。

示例： 已知 \(f(x)=\dfrac{5x}{x+3}\) ， \(f[g(x)]=4-x\) ，求 \(g(x)\) 的解析式。

示例： 已知 \(f(x)\) 是一次函数，且 \(f[f(x)]=2x-1\) ，求 \(f(x)\) 的解析式。

示例： 已知 \(2f(4x-3)+f(3-4x)=4x\) ，求 \(f(x)\) 的解析式。

示例： 二次函数 \(f(x)\) 满足 \(f(2)=-1,\ f(-1)=-1\) ，且 \(f(x)\) 的最大值为 \(8\) ，求 \(f(x)\) 的解析式。

示例： \(f(x)=\begin{cases}|x-1|-2,\ |x|\leq1\\\dfrac{1}{1+x^2},\ |x|>1\end{cases}\) ，则 \(f[f(\dfrac{1}{2})]=\)

A. \(\dfrac{1}{2}\)B. \(\dfrac{4}{13}\) C. \(-\dfrac{9}{5}\)D. \(\dfrac{25}{41}\)

示例： 定义在 \(\mathbb{N}\) 上的函数 \(f(n)\) 满足 \(f(n)=\begin{cases}n+13,\ n\leq2000\\f(f(n-18)),\ n>2000\end{cases}\) ，则 \(f(2002)=\)

示例： 如图，在直角坐标系中，\(\triangle{ABC}\) 是边长为 \(2\) 的等边三角形，直线 \(l:x=t\ (0\leq t\leq2)\) 截这个三 角形所得位于直线左侧的图形面积为 \(S=f(t)\)

1. 求 \(f(t)\) 的解析式；

2. 画出函数 \(S=f(t)\) 的图像。

答案：函数变换基础练习

示例： 写出变量代换后的的函数解析式（展开形式）：

1. \(f(x)=2x+1\) ，则 \(f(2x+1)=\uwave{4x+3}\)

2. \(f(x)=3-2x\) ，则 \(f(1-x)=3-2(1-x)=\uwave{2x+1}\)

3. \(f(t)=t^2+t\) ，则 \(f(1-m)=(1-m)^2+(1-m)=\uwave{m^2-3m+2}\)

4. \(g(m)=3-m^2\) ，则 \(g(m-n)=3-(m-n)^2=\uwave{-m^2+2mn-n^2+3}\)

示例： 写出复合后的函数解析式（展开形式）：

1. \(f(x)=3x+2,\ g(x)=2x+1\) ，则 \(f(g(t))=\uwave{6x+5}\)

2. \(f(x)=x-2,\ g(x)=2x^2+1\) ，则 \(g(f(t)+1)=2(x-1)^2+2=\uwave{2x^2-4x+4}\)

3. \(f(t)=2t+k,\ g(x)=3x-1\) ，则 \(g(2f(x))=\uwave{12t+6k-1}\)

4. \(f(t)=2t+1\) ，则 \(f(f(f(x)))=f(2(2t+1)+1)=f(4t+3)=\uwave{8t+7}\)

示例： 写出变量代换前的函数解析式：

1. \(f(2x+1)=4x+5\) ，则 \(f(x)=\uwave{2x+3}\)

2. \(f(1-2x)=4x+5\) ，则 \(f(x)=\uwave{-2x+7}\)

3. \(f(t+1)=t^2+2t+3\) ，则 \(f(x)=\uwave{x^2+2}\)

4. \(f(t+1)=t^2+t+3\) ，则 \(f(x)=(x-1)^2+(x-1)+3=\uwave{x^2-x+3}\)

提示 (4) 令 \(t+1=x\) ，则 \(t=x-1\)

☐

示例： 写出复合函数的母函数解析式

1. \(f(g(x))=2x+5,\ g(x)=2x\) ，则 \(f(x)=\uwave{x+5}\)

2. \(f(g(x))=2x+5,\ f(x)=2x\) ，则 \(g(x)=\uwave{x+2.5}\)

3. \(f(g(x))=x^2+2x,\ f(x)=x^2\) ，则 \(g(x)=\uwave{\sqrt{x^2+2x}}\)

4. \(f(g(x))=x^2+3x+2,\ f(x)=(1-x)^2\) ，则 \(g(x)=\uwave{1-\sqrt{x^2+3x+2}}\)

示例： 写出变换后的函数解析式：

1. \(f(x)=\dfrac{1}{x}\) ，则 \(f(x+1)+1=\uwave{\dfrac{x+2}{x+1}}\)

2. \(f(x)=\dfrac{1}{x}\) ，则 \(f(2-3x)-2=\dfrac{1}{2-3x}-2=\uwave{\dfrac{3-6x}{3x-2}}\)

3. \(f(x)=\dfrac{2}{x}\) ，则 \(f(1-x)+1=\dfrac{2}{1-x}+1=\uwave{\dfrac{x-3}{x-1}}\)

4. \(f(x)=\dfrac{k}{x}\) ，则 \(f(x+m)-n=\dfrac{k}{x+m}-n=\uwave{\dfrac{k-n(m+x)}{m+x}}\)

示例： 写出复合函数的母函数解析式：

1. \(f(x)=\dfrac{1+x}{x},\ f()g(x))=\dfrac{x}{x-1}\) ，则 \(g(x)=\uwave{x-1}\)

2. \(f(x)=\dfrac{x}{1-x},\ f(g(x))=\dfrac{3-x}{x-2}\) ，则 \(g(x)=\uwave{3-x}\)

3. \(f(x)=\dfrac{1+x}{1-x},\ f(g(x))=x\) ，则 \(g(x)=\uwave{\dfrac{x-1}{x+1}}\)

4. \(f(x)=\dfrac{1+x}{1-x},\ f(g(x))=\dfrac{1}{x}\) ，则 \(g(x)=\uwave{\dfrac{1-x}{x+1}}\)

提示 (1) 根据 \(f(x)=\dfrac{1+x}{x}\) 有 \(f(g(x))=\dfrac{1+g(x)}{g(x)}\)

☐

示例： 写出复合函数的母函数解析式：

1. \(g(x)=x+1,\ f(g(x))=x^2+1\) ，则 \(f(x)=\uwave{x^2-2x+2}\)

2. \(g(x)=2x+1,\ f(g(x))=x^2+1\) ，则 \(f(x)=\uwave{\dfrac{1}{4}x^2-\dfrac{1}{2}x+\dfrac{5}{4}}\)

3. \(g(x)=x+1,\ f(g(x))=\dfrac{1+x}{1-x}\) ，则 \(f(x)=\uwave{\dfrac{x}{2-x}}\)

4. \(g(x)=\dfrac{1-x}{1+x},\ f(g(x))=x\) ，则 \(f(x)=\uwave{\dfrac{1-x}{1+x}}\)

提示 (1) \(x=g(x)-1\) 代入 \(f(g(x))=x^2+1\)

得到 \(f(g(x))=(g(x)-1)^2+1=g^2(x)-2g(x)+2\)

☐

示例： 写出复合后的函数解析式：

1. \(f(x)=x+\dfrac{1}{x},\ g(x)=x+1\) ，则 \(f(g(x))=\uwave{\dfrac{x^2+2x+2}{x+1}}\)

2. \(f(x)=x+\dfrac{1}{x},\ g(x)=x^2+1\) ，则 \(f(g(x))=\uwave{\dfrac{x^4+2x^2+2}{x^2+1}}\)

3. \(f(x)=x+\dfrac{1}{x},\ g(x)=2-x\) ，则 \(f(g(x))=\uwave{\dfrac{x^2-4x+5}{2-x}}\)

4. \(f(x)=x+\dfrac{1}{x},\ g(x)=\dfrac{x+1}{x-1}\) ，则 \(f(g(x))=\uwave{\dfrac{2(x^2+1)}{x^2-1}}\)

示例： 写出复合函数的母函数解析式：

1. \(f(g(x))=x^3+\dfrac{1}{x^3},\ g(x)=x+\dfrac{1}{x}\) ，则 \(f(x)=\uwave{x^3-3x}\)

2. \(f(g(x))=\dfrac{x^3+x}{x^4+x^2+1},\ g(x)=x+\dfrac{1}{x}\) ，则 \(f(x)=\uwave{\dfrac{x}{x^2-1}}\)

3. \(f(g(x))=\dfrac{1}{x^2}(2x^4+3x^3+5x^2+3x+2),\ g(x)=x+\dfrac{1}{x}\) ，则 \(f(x)=\uwave{2x^2+3x+1}\)

4. \(f(g(x))=\dfrac{1}{x^2}(2x^4+3x^3+5x^2-3x+2),\ g(x)=x-\dfrac{1}{x}\) ，则 \(f(x)=\uwave{2x^2+3x+7}\)

示例： 将 \(f(x)\) 变形为 \(g(x)+\dfrac{k}{g(x)}+b\) 的形式：

1. \(f(x)=\dfrac{x^2+1}{x}=\uwave{x+\dfrac{1}{x}}\)(2) \(f(x)=2x+\dfrac{2}{x}=\uwave{2x+\dfrac{4}{2x}}\)

2. \(f(x)=\dfrac{2x^2+1}{x}=\uwave{2x+\dfrac{2}{2x}}\) (4) \(f(x)=\dfrac{2x^2-3x+3}{x-1}=\uwave{(2x-2)+\dfrac{4}{2x-2}+1}\)

示例： 求函数 \(f(x)\) 的解析式

1. \(2f(x)+f(\dfrac{1}{x})=x\) ，则 \(f(x)=\uwave{\dfrac{2x^2-1}{3x}}\)

2. \(2f(x)+f(1-x)=x\) ，则 \(f(x)=\uwave{x-\dfrac{1}{3}}\)

3. \(2f(x)+f(\sqrt{1-x^2})=x,\ x\in[0,1]\) ，则 \(f(x)=\uwave{\dfrac{2}{3}x-\dfrac{1}{3}\sqrt{1-x^2}}\)

解： (1) 将 \(x\) 代换为 \(\dfrac{1}{x}\) 后，得到方程组 \(\begin{cases} 2f(x)+f(\dfrac{1}{x})=x\\2f(\dfrac{1}{x})+2f(x)=\dfrac{1}{x} \end{cases}\)

☐

示例： 写出复合后的函数解析式：

1. \(f(x)=e^x,\ g(x)=\ln x\) ，则 \(f(g(x))=\uwave{x}\)

2. \(f(x)=xe^x,\ g(x)=\ln x\) ，则 \(f(g(x))=\uwave{x\ln x}\)

3. \(f(x)=\ln x,\ g(x)=e^{x}\) ，则 \(f(g(x))=\uwave{x}\)

4. \(f(x)=\ln x,\ g(x)=xe^x\) ，则 \(f(g(x))=\uwave{x+\ln x}\)

示例： 写出复合函数的母函数解析式：

1. \(f(g(x))=\dfrac{e^x}{e},\ f(x)=e^x\) ，则 \(g(x)=x-1\)

2. \(f(g(x))=e^x,\ g(x)=x-1\) ，则 \(f(x)=e^{x+1}\)

3. \(f(g(x))=e^{x+\ln 2-1},\ f(x)=2x\) ，则 \(g(x)=e^{x-1}\)

4. \(f(g(x))=e^{x+\ln 2-1},\ g(x)=e^x\) ，则 \(f(x)=\dfrac{2}{e}x\)

示例： 已知 \(y=f(x),\ x\in\mathbb{R}\) ，根据要求写出函数（或方程）解析式：

1. 图像与 \(y=f(x)\) 关于 \(x=1\) 成轴对称：\(\uwave{y=f(2-x)}\)

2. 图像与 \(y=f(x)\) 关于 \(y=1\) 成轴对称：\(\uwave{2-y=f(x)}\)

3. 图像与 \(y=f(x)\) 关于 \(x=y\) 成轴对称：\(\uwave{x=f(y)}\)

4. 图像与 \(y=f(x)\) 关于 \(x=-y\) 成轴对称：\(\uwave{-x=f(-y)}\)

示例： 已知 \(y=f(x),\ x\in\mathbb{R}\) ，根据要求写出函数（或方程）解析式：

1. 图像与 \(y=f(x)\) 关于点 \((0,1)\) 成中心对称：\(\uwave{1-y=f(-x)}\)

2. 图像与 \(y=f(x)\) 关于点 \((1,0)\) 成中心对称：\(\uwave{-y=f(1-x)}\)

3. 图像与 \(y=f(x)\) 关于点 \((1,1)\) 成中心对称：\(\uwave{1-y=f(1-x)}\)

4. 图像与 \(y=f(x)\) 关于点 \((a,b)\) 成中心对称：\(\uwave{b-y=f(a-x)}\)

示例： 根据已知条件，分析函数的对称性：

1. \(f(x)=f(1+x)\) (2) \(f(x)=f(1-x)\)

2. \(f(-x)=f(1+x)\) (4) \(f(-x)=f(1-x)\)

解： (1) \(f(x)\) 是周期函数，\(T=1\)

2. \(f(x)\) 图像关于 \(x=0.5\) 对称

3. \(f(x)\) 图像关于 \(x=0.5\) 对称

4. \(f(x)\) 是周期函数，\(T=1\)

   ☐

   
   

示例： 探究函数的周期性并证明。

1. \(f(x)\) 是偶函数，图像关于 \(x=1\) 对称；

2. \(f(x)\) 是偶函数，图像关于 \((1,0)\) 中心对称；

3. \(f(x)\) 是奇函数，图像关于 \(x=1\) 对称；

4. \(f(x)\) 是奇函数，图像关于 \((1,0)\) 中心对称；

解： (1) \(T=2\)(2) \(T=4\)

3. \(T=4\)(4) \(T=2\)

   ☐

   
   

示例： \(f(x)=\sin(\omega x+\phi)\) ，依据要求确定函数的参数，并绘制图像。

1. \(f(x)\) 是偶函数，图像关于 \(x=1\) 对称；

2. \(f(x)\) 是偶函数，图像关于 \((1,0)\) 中心对称；

3. \(f(x)\) 是奇函数，图像关于 \(x=1\) 对称；

4. \(f(x)\) 是奇函数，图像关于 \((1,0)\) 中心对称；

解： (1) \(f(x)=\sin\left(\pi x+\dfrac{\pi}{2}\right)\)

2. \(f(x)=\sin\left(\dfrac{\pi}{2}x+\dfrac{\pi}{2}\right)\)

3. \(f(x)=\sin\dfrac{\pi}{2}x\)

4. \(f(x)=\sin\pi x\)

   ☐

   
   

示例： \(f(x)=\cos(\omega x+\phi)\) ，依据要求确定函数的参数，并绘制图像。

1. \(f(x)\) 是偶函数，图像关于 \(x=1\) 对称；

2. \(f(x)\) 是偶函数，图像关于 \((1,0)\) 中心对称；

3. \(f(x)\) 是奇函数，图像关于 \(x=1\) 对称；

4. \(f(x)\) 是奇函数，图像关于 \((1,0)\) 中心对称；

解： (1) \(f(x)=\cos\pi x\)

2. \(f(x)=\sin\left(\dfrac{\pi}{2}x+\dfrac{\pi}{2}\right)\)

3. \(f(x)=\sin\dfrac{\pi}{2}x\)

4. \(f(x)=\sin\pi x\)

   ☐

   
   

示例： \(f(x)\) 是偶函数，周期为 \(2\) ，\(f(0.5)=2\) 。

☐

示例： \(f(x)\) 是奇函数，周期为 \(2\) ，\(f(0.5)=2\) 。

☐

示例： \(f(x)\) 是奇函数，且 \(f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

解： 函数以 \(4\) 为周期，给出一个周期的可以确定的函数值：

\(f(-0.5)=-1,\ f(0)=0,\ f(0.5)=1\)

\(f(1.5)=1,\ f(2)=0,\ f(2.5)=-1\)

于是全部可以确定的函数值为：

\(f(4k)=0,\ f(4k+2)=0\)

\(f(4k-0.5)=-1,\ f(4k+0.5)=1,\)

☐

示例： \(f(x)\) 是偶函数，且 \(f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

解： 函数以 \(2\) 为周期，给出一个周期的可以确定的函数值

\(f(-0.5)=f(0.5)=2\)

☐

示例： \(f(x)\) 是奇函数，且 \(-f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

解： 函数以 \(2\) 为周期，给出一个周期的可以确定的函数值

\(f(-0.5)=-2,\ f(0)=0,\ f(0.5)=2,\ f(1)=0\)

☐

示例： \(f(x)\) 是偶函数，且 \(-f(x)=f(2-x)\) ，\(f(0.5)=2\) 。

解： \(f(x)\) 以 \(4\) 为周期，给出一个周期的可以确定的函数值

\(f(\pm1)=0,\ f(\pm0.5)=-2,\ f(\pm1.5)=2\)

☐

答案：定义域和值域

示例： 求下列函数的定义域和值域。

1. \(f(x)=\dfrac{1}{x-|x|}\) \(\uwave{x\in(-\infty,0)}\)\(\uwave{f(x)\in(-\infty,0)}\)

2. \(f(x)=\dfrac{1}{1+\dfrac{1}{x}}\)\(\uwave{x\in\mathbb{R}\backslash \{-1,0\}}\)\(\uwave{f(x)\in\mathbb{R}\backslash \{0,1\}}\)

3. \(f(x)=\sqrt{-x^2-4x+5}\) \(\uwave{x\in[-5,1]}\)\(\uwave{f(x)\in[0,3]}\)

4. \(f(x)=\sqrt{x^2-6x+10}\) \(\uwave{x\in\mathbb{R}}\)\(\uwave{f(x)\in[1,+\infty)}\)

示例： \(\bigstar\)求下列函数的定义域和值域。

1. \(f(x)=\dfrac{\sqrt{4-x^2}}{x-1}\) \(\uwave{x\in[-2,1)\cup(1,2]}\)\(\uwave{f(x)\in\mathbb{R}}\)

2. \(f(x)=\sqrt{1-x}+\sqrt{x+3}-1\) \(\uwave{x\in[-3,1]}\)\(\uwave{f(x)\in[1\ ,\ 2\sqrt{2}-1]}\)

示例： 已知 \(f(x)=\begin{cases}x+2(x\leq-1)\\x^2\ (-1<x<2)\\2x\ (x\geq2)\end{cases}\) ，若 \(f(a)=3\) ，求 \(a\)

☐

示例： 若函数 \(y=\dfrac{ax-1}{\sqrt{ax^2+4ax+3}}\) 的定义域为 \(\mathbb{R}\) ，求 \(a\) 的取值范围。

解： \(0\leq a<\dfrac{3}{4}\)

☐

示例： 已知函数 \(y=\dfrac{2x-1}{x-1}\) 的值域是 \(\{y|y\leq0\}\cup\{y|y\geq3\}\) ，求此函数的定义域。

解： \(x\in[\dfrac{1}{2},1)\cup(1,2]\)

☐

示例： 已知 \(f(x+1)\) 的定义域为 \([-2,3)\) ，求 \(f(\dfrac{1}{x}+2)\) 的定义域。

解： \(x\in(-\infty,-1/3)\cup(1/2,\infty)\)

☐

示例： 已知扇形的周长为 \(10\) ，求扇形半径 \(r\) 和面积 \(s\) 的函数关系式 \(s(r)\) ，及此函数的定义域和值域。

☐

示例： 已知函数 \(y=f(x)\) 的定义域为 \((0,1]\) ，求 \(y=f(x^2)+f(x+1)\) 的定义域。

☐

示例： 求函数 \(y=2x-\sqrt{x-1}\) 的值域。

☐

示例： 已知函数 \(f(x)=|x-1|+|x-3|\)

1. 求函数 \(f(x)\) 的值域。

2. 若不等式 \(f(x)\geq a\) 对于一切实数都成立，求 \(a\) 的值。

提示 \(f(x)\) 意为数轴上一点到 \(1\) 与 \(3\) 的距离之和，

☐

示例： 已知 \(f(x-1)=|x|-|x-2|\) ，\(f(m)=f(2008)-\dfrac{7}{2}\) ，则 \(m\) 的值为：

A. \(-\dfrac{3}{4}\)B. \(-\dfrac{3}{2}\)C. \(-2\)D. \(2\)

☐

答案：单调性

示例： 判定函数 \(f(x)=\dfrac{ax}{x^2-1}\ (x\in(-1,1))\) 的单调性。

答案 当 \(a=0\) 时，\(f(x)\) 在 \((-1,1)\) 内是常数

\(a>0\) 时，\(f(x)\) 在 \((-1,1)\) 内单调递减

\(a<0\) 时，\(f(x)\) 在 \((-1,1)\) 内单调递增

☐

示例： 讨论函数 \(f(x)=x^2-2|x|-3\) 的单调区间。

☐

示例： 讨论函数 \(f(x)=-x^2+2|x|-3\) 的单调区间。

☐

示例： 讨论函数 \(f(x)=|x^2-2x-3|\) 的单调区间。

☐

示例： 讨论函数 \(y=|x|\cdot(1-x)\) 的单调区间。

☐

示例： 已知函数 \(f(x)\) 为 \(\mathbb{R}\) 上的减函数，则满足 \(f\left(\left|\dfrac{1}{x}\right|\right)<f(1)\) 的实数 \(x\) 的取值范围是

A. \((-1,1)\)B. \((0,1)\)C. \((-1,0)\cup(0,1)\)D. \((-\infty,-1)\cup(1,\infty)\)

☐

示例： 设函数定义在 \(\mathbb{R}\) 上，对于任意实数 \(m,n\) 恒有 \(f(m+n)=f(m)f(n)\) ，当 \(x>0\) 时， \(0<f(x)<1\)

• [(1)] 求证：\(f(0)=1\) 且当 \(x<0\) 时， \(f(x)>1\) ；
• [(2)] 求证：\(f(x)\) 在 \(\mathbb{R}\) 上单调递减；
• [(3)] 设集合 \(A=\{(x,y)|f(x^2)f(y^2)=f(1)\},\ B=\{(x,y)|f(ax-y+2)=1,a\in\mathbb{R}\}\) ，若 \(A\cap B=\Phi\) ，求 \(a\) 的取值范围。

解：

示例： 已知函数 \(f(x)=\dfrac{a+bx}{a-bx},\ x\in[-1,1]\) 。

1. \(a=1, b=3\) 时，证明 \(f(x)\) 在 \([-1,0]\) 上是增函数；

2. \(a>b>0\) 时，证明 \(f(x)\) 在 \([-1,1]\) 上是增函数；

3. 求函数 \(f(x)\) 的值域。

示例： (1) 证明函数 \(f(x)=\dfrac{x}{1+x^2}\) 在 \((-1,1)\) 上是增函数。

2. 讨论函数 \(f(x)=\dfrac{kx}{1+x^2}\) 在 \((-1,1)\) 上的单调性。

示例： 已知函数 \(f(x)=x^2-2ax+a^2-1\)

1. 若函数 \(f(x)\) 在区间 \([0,2]\) 上是单调的，求实数 \(a\) 的取值范围；

2. 当 \(x\in[-1,1]\) 时，求函数 \(f(x)\) 的最小值 \(g(a)\) ，并画出最小值函数 \(y=g(a)\) 的图像。

答案：函数的奇偶性

示例： 判断下列函数的奇偶性：

1. \(y=2x+\sqrt[3]{x}\)

2. \(y=|x+1|+|x-1|\)

3. \(y=x^2+x+1\)

4. \(f(x)=\begin{cases}x^2+2x-1\ &(x>0)\\0&(x=0)\\-x^2+2x+1\ &(x<0)\end{cases}\)

5. \(f(x)=\sqrt{1-x^2}+\sqrt{x^2+1}\)

6. \(\bigstar\ f(x)=\dfrac{\sqrt{1-x^2}}{|x+2|-2}\)

示例： 已知偶函数 \(f(x)\) 在区间 \([0,4]\) 上是增函数，试比较 \(f(-3)\) 与 \(f(\pi)\) 的大小。

☐

示例： 若奇函数 \(f(x)\) 在 \([3,7]\) 上的最小值是 \(5\) ，那么 \(f(x)\) 在 \([-7,-3]\) 上：

A. 最小值是 \(5\) B. 最小值是 \(-5\)

C. 最大值是 \(-5\) D. 最大值是 \(5\)

☐

示例： \(f(x)\) 是定义在 \(\mathbb{R}\) 上的奇函数，又 \(f(x)\) 在区间 \((0,+\infty)\)上是增函数，且 \(f(1)=0\) ，则满足 \(f(x)>0\) 的 \(x\) 的取值集合是 \(\_\_\_\_\_\_\)

☐

示例： 设 \(f(x)\) 是 \((-\infty,+\infty)\) 上的奇函数， \(f(x+2)=-f(x)\), 当 \(0\leq x\leq1\)时，\(f(x)=x\) ,则 \(f(7.5)\) 等于：

A. \(0.5\)B. \(-0.5\)C. \(1.5\)D. \(-1.5\)

☐

示例： 如果函数 \(f(x)\) 在 \(R\) 上为奇函数，在 \([-1,0)\) 上是增函数，且 \(f(x+2)=-f(x)\) , 试比较 \(f(\dfrac{1}{3}),\ f(\dfrac{2}{3}),\ f(1)\) 的大小关系 \(\_\_\_\_\_\_\_\_\_\)

☐

示例： 若 \(f ( x)\) 为奇函数，且在 \((0, +\infty )\) 内是增函数，又 \(f(-3)=0\) ，则 \(xf(x)<0\) 的解集为 \(\_\_\_\_\_\_\)

☐

示例： 设奇函数 \(f (x)\) 的定义域为 \([-5,5]\)，若当 \(x\in[0,5]\) 时, \(f (x)\) 的图象 如右图，则不等式 \(f(x)<0\) 的解是 \(\_\_\_\_\_\_\)

☐

示例： 已知 \(f(x)\) 是定义在 \(\mathbb{R}\) 上的奇函数，当 \(x\geq0\) 时， \(f(x)=x^2-2x\) ，则 \(f(x)\) 在 \(\mathbb{R}\) 上的表达式是

A. \(f(x)=x^2-2x\)B. \(f(x)=x(|x|-1)\)

C. \(f(x)=|x|(x-2)\)D. \(f(x)=x(|x|-2)\)

☐

示例： 函数 \(f(x)\) 是定义在 \([-6,6]\) 上的偶函数，且在 \([-6,0]\) 上是减函数，则

A. \(f(3)+f(4)>0\)B. \(f(-3)-f(2)<0\)

C. \(f(-2)+f(-5)<0\)D. \(f(4)-f(-1)>0\)

☐

示例： 设 \(f(x)\) 是定义在 \(\mathbb{R}\) 上的任意一个增函数，令 \(F(x)= f(x)-f(-x)\)，则 \(F(x)\) 必是

A. 增函数且是奇函数B. 增函数且是偶函数

C. 减函数且是奇函数D. 减函数且是偶函数

☐

示例： 设 \(f(x),g(x)\) 都是奇函数， \(F(x)=f(x)+g(x)+3\) ，若 \(F(5)=9\) ，则 \(F(-5)=\)

A. \(3\) B. \(-3\) C. \(-6\) D. \(-9\)

☐

示例： 设 \(f(x),\ g(x)\) 都是奇函数，且 \(F(x)=af(x)+bg(x)+2\) ，若在 \((0, +\infty)\) 上 \(F(x)\) 有最大值 \(8\)，则在 \((-\infty, 0)\) 上 \(F(x)\) 有

A. 最小值 \(-8\)B. 最大值 \(-8\)C. 最小值 \(-4\)D. 最小值 \(-6\)

☐

示例： 函数 \(f(x)=\dfrac{\sqrt{1-x^2}}{|x+3|-3}\) 是

A. 奇函数B. 偶函数C. 既奇又偶函数D. 无确定奇偶性

☐

示例： 若 \(f(x)=ax^2+bx+c\ (a\neq0)\) 是偶函数，则 \(g(x)=ax^3+bx^2+cx\) 是

A. 奇函数B. 偶函数C. 既奇又偶函数D. 无确定奇偶性

☐

示例： 下列命题中真命题个数是

1. 偶函数图象一定与 \(y\) 轴相交

2. 奇函数图象一定过原点

3. 偶函数图象关于 \(y\) 轴对称

4. 既奇又偶函数一定满足 \(f ( x) = 0\)

A. \(1\) B. \(2\)C. \(3\)D. \(4\)

☐

示例： 若奇函数 \(f (x)\) 在区间 \([3,7]\) 上是增函数，且最小值为 \(5\) ，那么在区间 \([-7,-3]\) 上是( )

A. 增函数且最小值为 \(-5\) B. 增函数且最大值为 \(-5\)

C. 减函数且最小值为 \(-5\) D. 减函数且最大值为 \(-5\)

☐

示例： 下列四个命题中正确的个数是

1. \(f(x)=1\) 是偶函数;

2. \(g(x)=x^3, x\in (-1,1]\) 是奇函数;

3. 若 \(f(x)\) 是奇函数，\(g(x)\)是偶函数，则 \(H(x)= f(x)\cdot g(x)\)一定是奇函数;

4. 函数 \(y=f(x)\) 的图象关于 \(y\) 轴对称。

A. \(1\)B. \(2\)C. \(3\)D. \(4\)

☐

示例： 已知\(f(x)=x^4+ax^3+bx-8\)，且 \(f(-2)=10\)，则\(f(2)=\)

☐

示例： 判断下列函数的奇偶性:

1. \(\begin{cases} x+1\ &(x>0)\\1 &(x=0)\\-x+1&(x<0) \end{cases}\)

2. \(f(x)\) 不恒为 \(0\) ，且对 \(a,b\in\mathbb{R}\) 恒有 \(f(a+b)=f(a)+f(b)\)

☐

示例： 已知 \(f(x)\) 是定义在 \(\mathbb{R}\) 上的奇函数，当 \(x>0\) 时, \(f(x)=\sqrt{x}+1\) ，则 $f (x) = $

☐

示例： 函数 \(f(x)\) 的定义域为 \(\mathbb{R}\) ，若 \(f(x+1)\) 与 \(f(x-1)\) 都是奇函数，则：

A. \(f(x)\) 是偶函数 B. \(f(x)\) 是奇函数

C. \(f(x)=f(x+2)\)D. \(f(x+3)\) 是奇函数

☐

示例： 是否存在常数\(m,n\)，使函数 \(f(x)=(m^2-1)x^2+(m-1)x+n+2\) 为奇函数？

☐

示例： 已知 \(f(x),g(x)\) 均为奇函数，且定义域相同。

求证： \(f(x)+g(x)\) 为奇函数， \(f(x)\cdot g(x)\) 为偶函数。

☐

示例： 设函数 \(y= f(x)\) 对于任意的 \(x,y\in R\) 都有 \(f(x+y)= f(x)+ f(y)\) ，且 \(f(x)\) 不恒为零，判断 \(f(x)\) 的奇偶性。

答案 奇函数但不是偶函数

示例： 已知函数 \(f(x)\) 满足 \(f(x+y)+f(x-y)=2f(x)\cdot f(y)\ (x,y\in\mathbb{R})\) ，且 \(f(0)\neq0\) ，判定函数 \(f(x)\) 的奇偶性并证明。

答案 令 \(x=y=0\) 得到 \(2f(0)=2f^2(0)\) ，由于 \(f(0)\neq0\) ，

因此 \(f(0)=1\)

☐

示例： 已知函数 \(y=f(x)\) 为奇函数，在 \((0,+\infty)\) 内是减函数，且 \(f(x)<0\) ，试问：\(F(x)=\dfrac{1}{f(x)}\) 在 \((-\infty,0)\) 内增减性如何？并证明之。

答案 单调递减，证明略。

示例： 已知偶函数 \(f(x)\) 的定义域时 \(\mathbb{R}\) ，当 \(x<0\) ， \(f(x)=x^2-3x-1\) ，求 \(f(x)\) 的解析式。

答案 略

示例： 已知奇函数 \(f(x)\) 的定义域时 \(\mathbb{R}\) ，当 \(x>0\) ， \(f(x)=x^2+2x-1\) ，求 \(g(x)\) 的解析式。

答案 略

示例：

1. \(f(x)\) 是定义在 \(\mathbb{R}\) 上的偶函数，且当 \(x\leq0\) 时，\(f(x)=x^2-x\)，求 \(f(x)\) 的解析式.并画出函数图象，求出函数的值域;

2. 已知 \(f(x)\) 是定义在R上的奇函数，当 \(x>0\) 时 \(f(x)=x^2-4x+3\) ，求 \(f(x)\) 的解析式.

示例： 已知函数 \(f (x)\)是定义在区间 \([-2,2]\) 上的偶函数，当 \(x\in[0,2]\)时， \(f (x)\)是减函数，如果不等式 \(f(1-m)<f(m)\) 成立，求实数 \(m\) 的取值范围。

示例： 已知函数 \(f(x)\) 定义域 \(\mathbb{R}\) ，为对任意的 \(x1,x2\in\mathbb{R}\) 都有 \(f(x1 +x2)= f(x1)+ f(x2)\) 且 \(x>0\) 时 \(f (x)<0,\ f(1)=-2\)，试判断在区间 \([-3,3]\) 上 \(f(x)\) 是否有最大值和最小值？如果有试求出最大值和最小值，如果没有请说明理由。

示例： 已知函数 \(f(x)\) 定义域 \(\mathbb{R}\) ,为对任意的 \(x1,x2\in\mathbb{R}\) 都有 \(f(x1 +x2)= f(x1)f(x2)\) 且 \(x>0\) 时 \(0<f (x)<1\) ，求 \(f(0)\) 的值并求 \(x<0\) 时 \(f(x)\) 的取值范围。

答案：反函数

示例： 函数 \(y=\sqrt{-x},\ (x\leq0)\) 的反函数是：

A. \(y=x^2\ (x\geq0)\)B. \(y=-x^2\ (x\geq0)\)

C. \(y=x^2\ (x\leq0)\)D. \(y=-x^2\ (x\leq0)\)

☐

示例： 已知 \(y=x|x|+2x\) ，求 \(f^{-1}(x)\)

☐

示例： 设 \(P(1,2)\) 在 \(f(x)=ax^2+b,\ (x\geq0)\) 的图像上，又在它的反函数图像上，求 \(f^{-1}(x)\) 。

☐

答案：综合问题

示例： 已知 \(y=f(x)\) 表示过点 \((0,-2)\) 的直线， \(y=g(x)\) 表示过点 \((0,0)\) 的直线，又 \(f(g(x))=g(f(x))=3x-2\) ，求两直线交点坐标。

☐

示例： 写出图 13 所示函数的定义，要求使用绝对值记法而非分段函数。

☐

示例： 已知 \(f(\dfrac{x+1}{x})=\dfrac{x^2+1}{x^2}+\dfrac{1}{x}\) ，求 \(f(x)\) 。

☐

示例： 已知 \(2f(x^2)+f(\dfrac{1}{x^2})=x\ (x>0)\) ，求 \(f(x)\)

☐

示例： 定义 \(f_n(x)\) ：\(n=1\) 时 \(f_1(x)=f(x)\) ； \(n\) 为大于 \(1\) 的自然数时 \(f_n(x)=f(f_{n-1}(x))\) 。

若 \(f(x)=\dfrac{x}{\sqrt{1-x^2}}\) ，求 \(f_n(x)\) 。

☐

示例： 已知，定义在 \(\mathbb{R}\) 上的函数 \(f(x)\) 是以 \(2\) 为周期的函数，且当 \(x\in[0,2]\) 时， \(f(x)=|x+1|\) ，求 \(x\in\mathbb{R}\) 时， \(f(x)\) 的解析式。

☐

示例： 求 \(f(x)=x-\sqrt{1-2x}\) 的值域。

☐

示例： 求 \(f(x)=\dfrac{a+bx}{a-bx}\ (a>b>0),\ x\in[-1,1]\) 的值域。

示例： 求 \(f(x)=\dfrac{x^2-x+1}{x^2+x+1}\) 的值域。

☐

示例： 已知 \(f(x)=\dfrac{5x}{x+3}\) ， \(f[g(x)]=4-x\) ，求 \(g(x)\) 的解析式。

答案 \(\dfrac{12-3x}{x+1}\)

示例： 已知 \(f(x)\) 是一次函数，且 \(f[f(x)]=2x-1\) ，求 \(f(x)\) 的解析式。

答案 \(\sqrt{2}x+1-\sqrt{2}\) \(-\sqrt{2}x+1+\sqrt{2}\)

示例： 已知 \(2f(4x-3)+f(3-4x)=4x\) ，求 \(f(x)\) 的解析式。

答案 \(x+1\)

示例： 二次函数 \(f(x)\) 满足 \(f(2)=-1,\ f(-1)=-1\) ，且 \(f(x)\) 的最大值为 \(8\) ，求 \(f(x)\) 的解析式。

答案 \(-4x^2+4x+7\)

示例： \(f(x)=\begin{cases}|x-1|-2,\ |x|\leq1\\\dfrac{1}{1+x^2},\ |x|>1\end{cases}\) ，则 \(f[f(\dfrac{1}{2})]=\)

A. \(\dfrac{1}{2}\)B. \(\dfrac{4}{13}\) C. \(-\dfrac{9}{5}\)D. \(\dfrac{25}{41}\)

答案 \(B\)

示例： 定义在 \(\mathbb{N}\) 上的函数 \(f(n)\) 满足 \(f(n)=\begin{cases}n+13,\ n\leq2000\\f(f(n-18)),\ n>2000\end{cases}\) ，则 \(f(2002)=\)

答案 \(2010\)

示例： 如图，在直角坐标系中，\(\triangle{ABC}\) 是边长为 \(2\) 的等边三角形，直线 \(l:x=t\ (0\leq t\leq2)\) 截这个三 角形所得位于直线左侧的图形面积为 \(S=f(t)\)

1. 求 \(f(t)\) 的解析式；

2. 画出函数 \(S=f(t)\) 的图像。

答案 (1) \(\begin{cases} \dfrac{\sqrt{3}}{2}t^2\qquad&(0\leq t\leq1)\\\sqrt{3}-\dfrac{\sqrt{3}}{2}(2-t)^2 &(1<t\leq2) \end{cases}\)

2. 略