几何证明基础（Euclid-Vol.I）
角的定义
示例： 描述直角的定义。
本页的习题体现了“等量加（减）等量，其和（差）仍相等”这一基本公理。
提示：利用直角的定义
示例： 证明对顶角相等。
本题得到的等角结论将广泛应用于“图形绕一点旋转模型”
示例： 设相邻两个角 \(\angle{AOC}\) 、 \(\angle{COB}\) 互补（邻补角），且 \(\angle{AOC}\) 、 \(\angle{COB}\) 的平分线分别为 \(OD\) 、 \(OE\) ，求证 \(OD\perp OE\) 。
示例： 设邻角 \(\angle{AOB}\) 、 \(\angle{BOC}\) 的平分线分别为 \(OM\) 、 \(ON\) ，且 \(OM\perp ON\) ，求证 \(OA\) 、 \(OC\) 成一条直线。
等价关系（充分必要条件）
“若 \(A\) 则 \(B\) （\(A\Rightarrow B\)）”并且“若 \(B\) 则 \(A\)（\(A\Leftarrow B\)）”，意味着 \(A\) 与 \(B\) 等价，称 \(A\) 与 \(B\) 互为充分必要条件，记作 \(A\Leftrightarrow B\) 。
示例： 描述前面两道证明题反映出的等价关系。
在数学学习中，等价关系是非常重要的。你可以放心利用等价关系转换条件，因为等价关系不会让你遗漏或添加问题的解，也不会在证明时加强或减弱条件。
示例： 设邻角 \(\angle{AOB}\) 、 \(\angle{BOC}\) 的角平分线分别为 \(OM\) 、 \(ON\) ，求证 \(\angle{MON}=\dfrac{1}{2}(\angle{AOB}+\angle{BOC})=\dfrac{1}{2}\angle{AOC}\)
从特殊到一般
“邻角的角平分线夹角是邻角和的一半”相对于“邻补角角平分线垂直”是更一般性的结论。一般性提供了更高层次的统一视角，特殊性提供了在某些情况下的简化。
在上面的题目中，角平分线的夹角只与 \(\angle{AOC}\) 的大小有关，与 \(OB\) 的位置变化无关。很多时候数学研究就是要找出这种“变化之中的不变量”。将角度变为长度，就得到下面的示例。
示例： 线段 \(AB\) 长度为 \(4\) ，\(C\) 是线段 \(AB\) 上一点， \(D,E\) 分别是 \(AC\) 和 \(BC\) 的中点。求线段 \(DE\) 的长度。
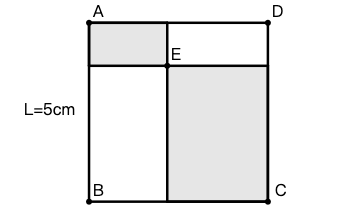
示例： 右图中 \(ABCD\) 为正方形，边长为 \(5cm\) 。阴影部分为矩形，求阴影部分的周长。
截平行线的角
接下来要使用平行线的“三线八角”以及“三角形内角和定理”
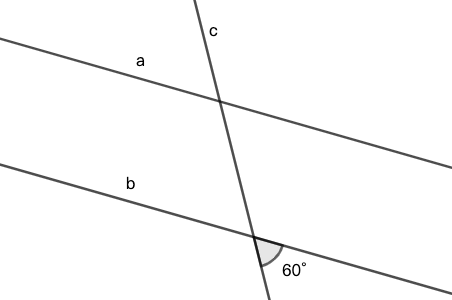
示例： 在下图中，直线 \(a\) 与直线 \(b\) 平行，直线 \(c\) 与直线 \(b\) 的一个夹角为 \(60^\circ\) ，标出图中其它角的角度。
两直线平行时：同位角相等、内错角相等、外错角相等；同旁内角互补、同旁外角互补。反之亦然。这是欧氏几何对空间的基本假设。初学者要锻炼在复杂图形中看出这些关系并加以利用的能力。
几何图形中看出数量关系的“眼力”对解题很重要
示例： 证明垂直于同一条直线的两条直线互相平行。
示例： 直线 \(AB\) 平行于直线 \(CD\) ，若直线 \(XY\perp CD\) 垂直时，也必与 \(AB\) 垂直。
示例： 分别垂直于两条平行线 \(AB\) 、 \(CD\) 的两条直线 \(EF\) 、 \(GH\) 互相平行。
平移操作
通过平行线带来的诸角相等，可以在平面通过平移操作“传递”等角关系。在几何证明中，往往不能直接使用“平移”的概念，你需要使用平行线的“三线八角”来达到“平移”的效果。
公理和定义
在下面两道题目中，你只能使用平行公理“过直线外一点能且只能做一条直线与已知直线平行”以及平行线的定义“平面上的两条没有交点的直线”来证明命题。
示例： 在一平面内有三条直线 \(a,b,c\) ，且 \(a\parallel b\) ， \(a\parallel c\) ，求证 \(b\parallel c\) 。
示例： 在同一条平面上的直线 \(a,b,c,d\) ，\(a\) 与 \(b\) 相交、 \(c\parallel a\) 、 \(d\parallel b\) 。求证，\(c\) 与 \(d\) 相交。
看似直观简单的命题，证明往往更不容易。这些问题是初学者学习数学证明的绝佳例子。
在下面三道题目中，提到了“同向平行”和“逆向平行”的概念。根据题目揣摩一下这两个概念是什么意思。
示例： 直线 \(EF\) 截平行线 \(AB\) 、 \(CD\) ，求证内错角的平分线平行，同位角的平分线也平行。
示例： 若 \(\angle{BAC}\) 的两边 \(AB\) 、 \(AC\) 分别与 \(\angle{EDF}\) 的两边 \(DE\) 、 \(DF\) 平行，则两个角的平分线 \(AM\) 、 \(DN\) 互相平行或垂直。
示例： 若两线段 \(AB\) 、 \(CD\) 同向平行， \(P\) 为 \(AB\) 、 \(CD\) 之间（此处意思是四边形 \(ABCD\) 内部）一点。求证：\(\angle{ABP}+\angle{CDP}=\angle{BPD}\) 。
辅助线是解决平面几何问题时常用的工具。很多辅助线都是有规律可循的，要注意总结辅助线的常见模式。
示例： 若两线段 \(AB\) 、 \(CD\) 同向平行， \(P\) 为直线 \(AB\) 、 \(CD\) 之外一点。求证：\(|\angle{ABP}-\angle{CDP}|=\angle{BPD}\) 。
考虑到多种情形
在上述题目中，文字描述的情形不止一种，你需要小心处理。
三角形的角
示例： 利用平行线的“三线八角”，证明三角形内角和等于平角（三角形内角和定理）。
公理体系
数学命题之间，并不存在谁先谁后。人为地将一些命题至于更“靠前”，用它们来推导另一些命题，是人类组织数学知识的方法。
示例： 证明三角形的外角等于不相邻的两内角之和。
本题要利用到“等腰三角形的底角相等”这一性质
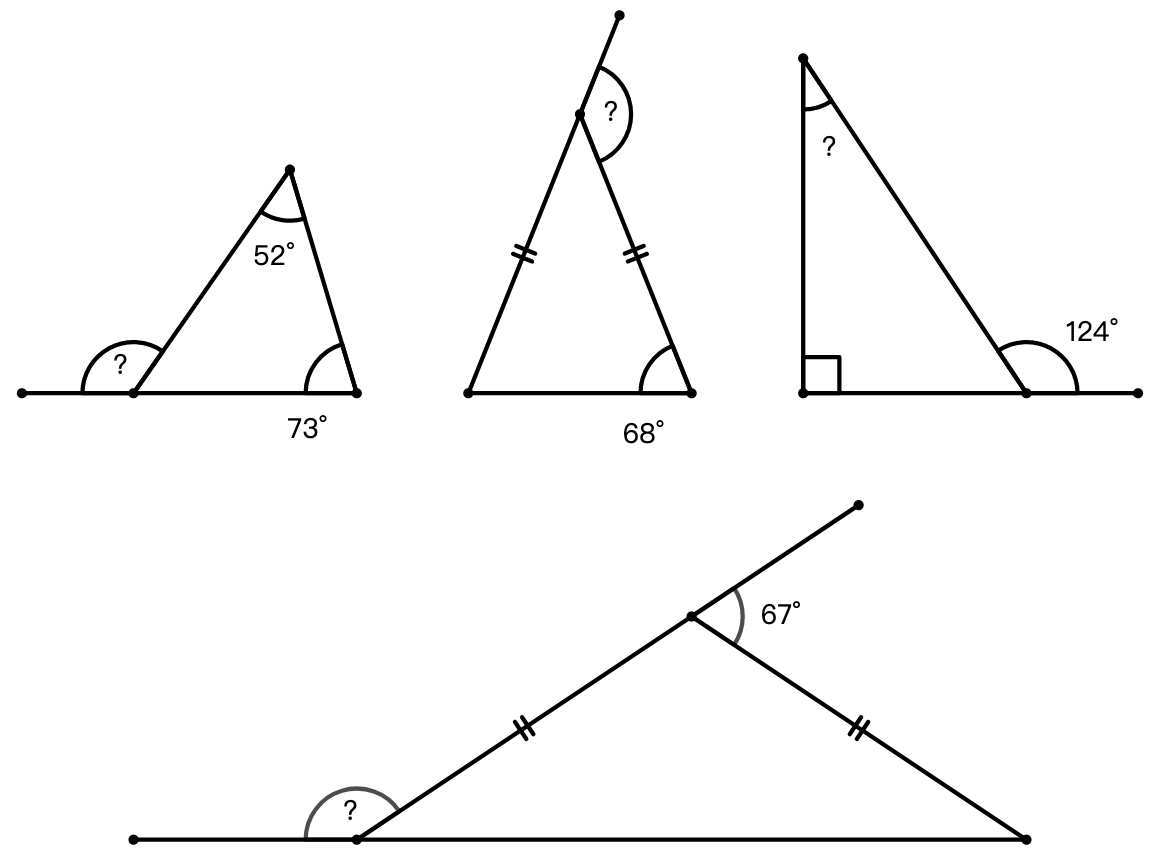
示例： 证明三角形的外角和等于 \(360^\circ\)
示例： 证明简单四边形（四条边不相交）的内角和等于 \(360^\circ\)
示例： 简单四边形的外角和等于多少度？证明之。
示例： 五边形、六边形的内角和及外角和分别是多少？据此猜测简单 \(n\) 边形的内角和及外角和。
示例： 证明你提出的简单 \(n\) 边形内角和与外角和公式。
归纳、猜想和证明
通过观察特殊示例，猜想规律，进一步验证规律并证明，这是重要的数学研究手段。学习数学和解题时，这种思维方式也有很大助益。
示例： 两边分别垂直的两个角，角度关系如何？
全等三角形
全等三角形的判定 (SAS)
定理： 如果两个三角形中，一个的两边分别等于另一个两边，且相等线段所夹的角相等。那么这两个三角形全等。 (Euclid I.4)
全等三角形的判定 (SSS)
定理： 如果一个三角形的三条边与另外一个三角形的三条边都相等，那么等边所夹的角也都相等。 (Euclid I.8)
全等三角形的判定 (ASA)
定理： 如果两个三角形中，有两对角分别相等，且有一条边相等（这条边或者是等角之间的边，或者是任意等角的对边），那么这两个三角形全等。(Euclid I.26)
\(\triangle{ABC} \cong \triangle{A‘B’C‘}\)
全等三角形的符号
如果 \(\triangle{ABC}\) 与 \(\triangle{A‘B’C‘}\) 全等，记作 \(\triangle{ABC} \cong \triangle{A‘B’C‘}\) 。注意，字母的排列次序应当和三角形的边角相等的对应次序一样，即应当有 \(AB=A'B',BC=B'C',CA=C'A'\) 。
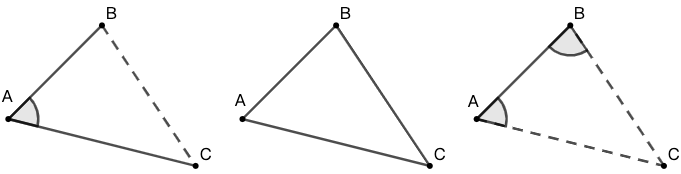
思考与讨论
- 初学者常常误用“边边角”进行全等三角形判定。即在 \(\triangle{ABC}\) 与 \(\triangle{A'B'C'}\) 中， \(AB=A'B'\)，\(BC=B'C'\)，\(\angle{C}=\angle{C'}\) 就得出三角形全等的结论。这是不对的，你能画图说明为什么这种判定方法不对么？
- 你如何证明上述全等三角形判定定理？请注意，这些判定是非常基本的定理，你无法使用更“高级”的结论来证明这些定理。在你的证明过程中，你使用了哪些公理、公设或定理呢？审视一下你的证明是不是构建在更为基本的命题上。
示例： (Euclid I.4) 证明两边及其夹角对应相等的两个三角形全等。（SAS）
提示 这是欧几里得《几何原本》中非常靠前的一个结论，此时几乎没有任何可以使用的定理。证明的思路是从“角”的定义出发证明两个三角形重合。
角平分线
全等三角形的判定定理是非常基础的定理，有许多其它结论都是从全等三角形导出。下面让我们用其来证明角平分线作图的正确性。
示例： (Euclid I.9) 证明角平分线的作图成立。
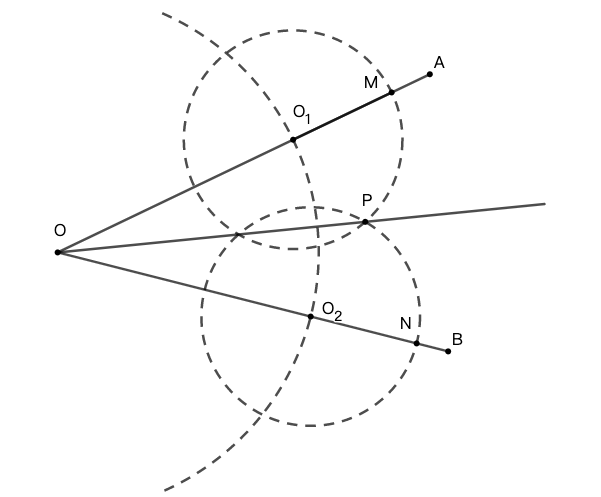
证明 这是典型的利用全等三角形证明的命题。证明的思路是证明 \(\triangle{OO_1P}\) 和 \(\triangle{OO_2P}\) 全等，从而得到 \(\angle{O_1OP}=\angle{O_2OP}\) 。证明步骤如下：
- 由于点 \(O_1\) 和 \(O_2\) 在圆 \(O\) 上，所以 \(OO_1=OO_2\) 。
圆的定义
- 由于圆 \(O_1\) 和圆 \(O_2\) 半径相同，所以 \(O_1P=O_2P\) 。
圆的定义
- 在 \(\triangle{OO_1P}\) 和 \(\triangle{OO_2P}\) 中 \(OP=OP, OO_1=OO_2, O_1P=O_2P\) ，因此 \(\triangle{OO_1P} \cong \triangle{OO_2P}\)
三角形全等判定定理(SSS)
- 因此 \(\angle{O_1OP}=\angle{O_2OP}\) ，证毕。
☐
全等三角形对应角相等
示例： 证明角平分线上的点到角的两边距离相等。
示例： 证明角的两边距离相等的点在角平分线上。
等腰三角形
示例： (Euclid I.5) 证明等腰三角形的两底角相等。等腰/等边三角形的性质
定理： 等腰三角形两底角相等（另一个说法是“等边对等角”） (Euclid I.5)
请注意：上述命题的逆命题也是成立的：
定理： 有两个角相等的三角形是等腰三角形（另一个说法是“等角对等边”）(Euclid I.6)
这件事情并不好证明，在《几何原本》，这是第 I 卷的第 5 命题，在此之前只有一个较为强大的工具：“边角边”全等判定定理。
示例： (Euclid I.6) 证明三角形中等角对等边。
等腰三角形“三线合一”
在等腰三角形中，顶角的角平分线、底边上的高以及底边上的中线位于同一条直线上。这是一个在初中教科书上明确给出的结论，在参加诸如中考一类的考试时，你可以将其简称为“三线合一”。
示例： 证明等腰三角形的顶角平分线垂直且平分底边。
示例： 证明等腰三角形底边的垂直平分线是顶角的平分线。注意：你不能直接“默认”底边的垂直平分线经过顶点，你需要证明这一点
思考与讨论
- 你需要证明哪些命题，才能说明“三线合一”中的三条线的等价关系？
平行四边形
平行四边形 (Parallelogram) 的定义
定义： 两组对边分别平行的四边形叫做平行四边形。
小学课内教学中，在“认识图形”时，平行四边形的定义和性质是一同介绍的。但单独从字面上看，“平行四边形”只包含了“对边平行”，其它性质诸如对边对角相等、中心对称等性质，需要从定义中证明出来。
平行四边形的对边对角关系
定理： 四边形如果由两条对边平行且相等，则另一组对边也平行且相等。(Euclid I.33)
定理： 四边形的两组对边分别平行（平行四边形），则对边对角彼此相等，且对角线二等分该四边形。(Euclid I.34)
平行四边形的性质是“很好的性质”，具体地说就是这些性质的逆命题都成立。例如，平行四边形的对角相等，（逆命题）对角相等的四边形是平行四边形。再比如，平行四边形的对边相等，（逆命题）对边相等的四边形是平行四边形。
习惯上使用“反之亦然”(“and vice versa”)表示命题的逆命题成立。例如：“平行四边形的对角相等，反之亦然”。
示例： 证明对于平面上的简单四边形（各边不相交）来说，以下三个命题是等价命题：
“两组对边分别平行”
“两组对角分别相等”
“一组对边平行且相等”
平行四边形的面积
定理： 同底且在相同平行线之间的平行四边形彼此面积相等。(Euclid I.35)
上述定理保证了平行四边形的面积等于底乘以高，即在两平行线之间同底的矩形的面积。如果平行四边形的底长度为 \(b\) ，高为 \(h\) ，则平行四边形的面积 \(S\) 的计算方法为 \(S=b\cdot h\) 。
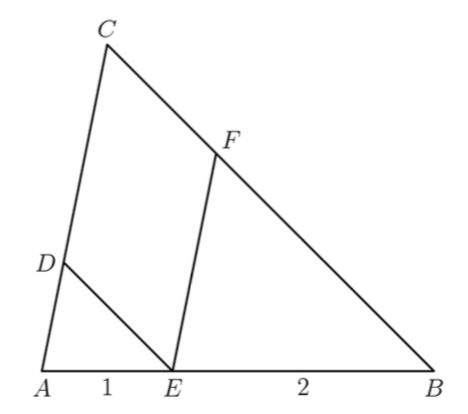
平行四边形面积性质的证明示例： (Euclid I.35) 在图 3 中， \(AF\parallel BC\) ，求证四边形 \(ABCD\) 和 \(CBEF\) 面积相同。
证明 (1) \(AD=BC=EF\) （平行四边形对边相等）
\(AE=AD+DE=DE+EF=DF\) （等量加等量，其和仍相等）
\(\angle{BAE}=\angle{CDF},\angle{AEB}=\angle{DFC}\) （同位角相等）
\(\triangle{ABE}\cong\triangle{DCF}\) （全等三角形判定(ASA)）
\(S_{ABCD}=S_{\triangle{ABE}}-S_{\triangle{GDE}}-S_{\triangle{GBC}}\)
\(S_{CBEF}=S_{\triangle{DCF}}-S_{\triangle{GDE}}-S_{\triangle{GBC}}\)
综上所述， \(S_{ABCD}=S_{CBEF}\) 。☐
思考与讨论
- 紧接着上述命题的证明，欧几里得在《几何原本》证明了一系列命题，终于得到了我们所熟知的“三角形面积”的各种性质。阅读《几何原本》的相关章节，看看欧几里得在“三角形的面积”之后证明了哪些命题。
勾股定理的证明
示例： 将《几何原本》第一卷第 47 命题（勾股定理）的证明过程改写成中学几何证明风格。
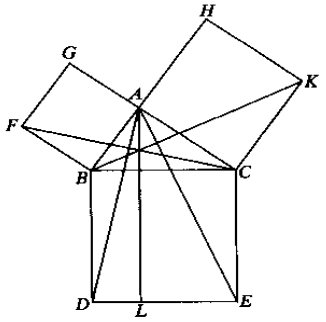《几何原本》的证明图示例： 用赵爽弦图（三国时期的数学家）证明勾股定理。
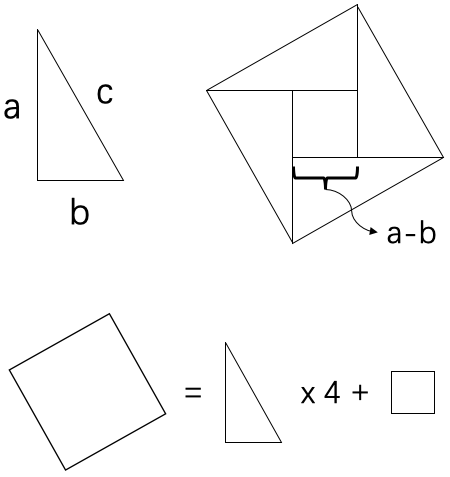赵爽弦图示例： 图 6 是第十二任美国总统加菲尔德1863年发表在一份期刊上的勾股定理证明的配图（利用了梯形面积），请写出其证明。
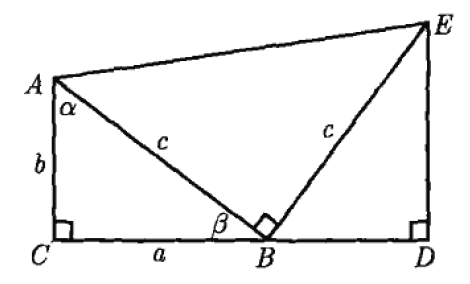美国总统的证明图
- 因此 \(\angle{O_1OP}=\angle{O_2OP}\) ，证毕。
- 在 \(\triangle{OO_1P}\) 和 \(\triangle{OO_2P}\) 中 \(OP=OP, OO_1=OO_2, O_1P=O_2P\) ，因此 \(\triangle{OO_1P} \cong \triangle{OO_2P}\)
- 由于圆 \(O_1\) 和圆 \(O_2\) 半径相同，所以 \(O_1P=O_2P\) 。