圆：常见辅助线

积累一些常见的辅助线技巧，有利于在解题时快速找到思路，从而节省时间。技巧总是来源于基本原理，技巧的运用建立在对基本原理的熟练掌握之上。

看见弦做半径

\(AB\) 为圆 \(O\) 的弦，连接 \(OA\) 、 \(OB\) ，有 \(OA=OB\) 。

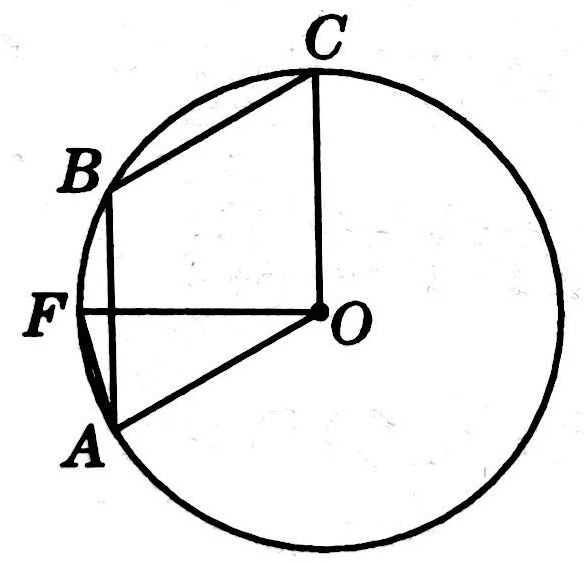
示例：如图 1 所示，点 \(A,B,C\) 是圆 \(O\) 上的三点，且四边形 \(ABCO\) 是平行四边形， \(OF\perp OC\) 交圆 \(O\) 于点 \(F\) ，求 \(\angle{BAF}\) 。

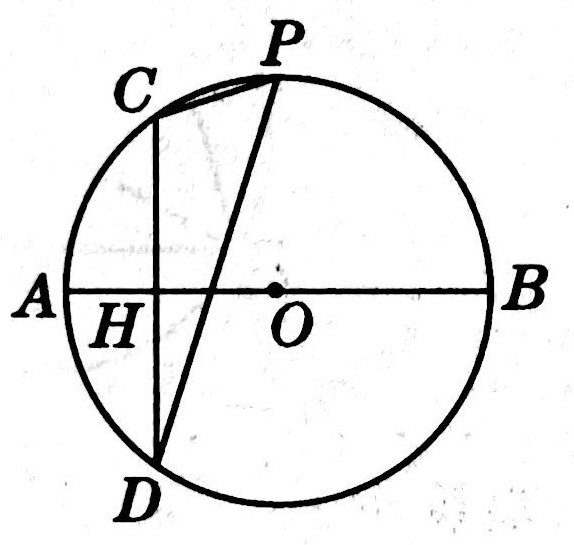
示例：如图 2 线段 \(AB\) 是圆 \(O\) 的直径，弦 \(CD\perp AB\) 于点 \(H\) ，\(P\) 是 \(\wideparen{CBD}\) 上任意一点， \(AH=2\) ，\(CH=4\) 。

（1）求圆 \(O\) 半径 \(r\) 的长度；

（2）求 \(\sin\angle{CPD}\) 。

弦心距

做出弦心距线段，从而利用垂径定理得到平分弦的条件，使用勾股定理，或者利用等弦的弦心距也相等的性质。

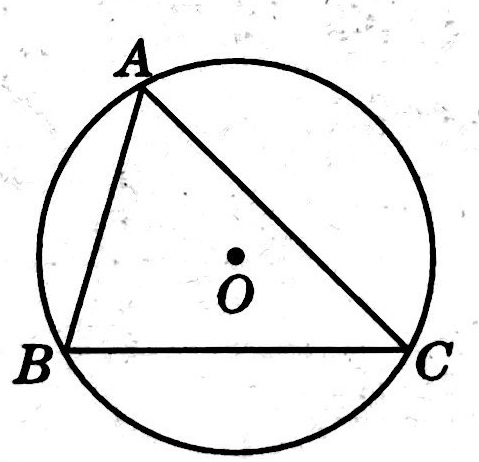
示例：如图 3 所示，已知圆 \(O\) 的半径为 \(2\) ，弦 \(BC\) 的长为 \(2\sqrt{3}\) ，点 \(A\) 为弦 \(BC\) 所对优弧上任意一点（\(B,C\) 两点除外）。

（1）求 \(\angle{BAC}\) 的度数；

（2）求 \(\triangle{ABC}\) 面积的最大值。

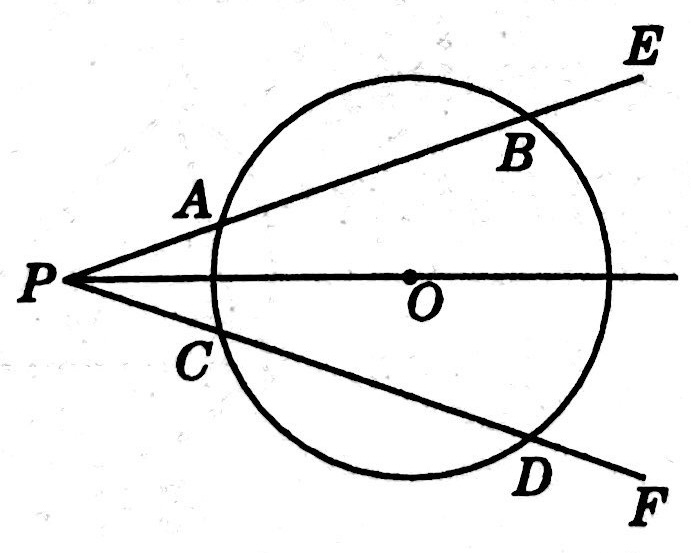
示例：如图 4 所示，点 \(O\) 是 \(\angle{EPF}\) 平分线上一点，圆 \(O\) 与角的两边分别交于 \(A,B\) 和 \(C,D\) 。求证 \(AB=CD\) 。

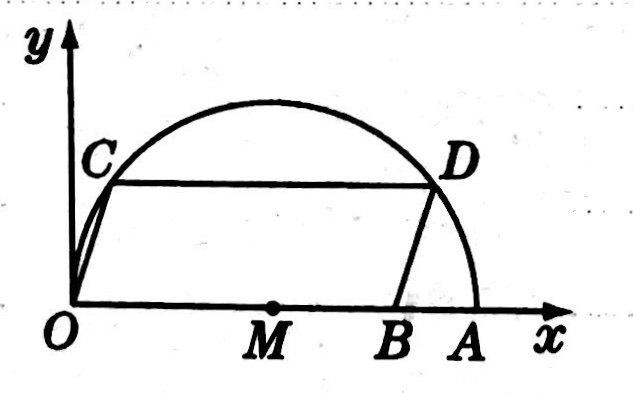
示例：如图 5 所示，在平面直角坐标系中，点 \(A\) 的坐标是 \((20,0)\) ，点 \(B\) 点坐标是 \((16,0)\) ，点 \(C,D\) 在以 \(OA\) 为直径的半圆 \(M\) 上，且四边形 \(OCDB\) 是平行四边形。求点 \(C\) 的坐标。

等弧等弦

（1）连接等弧得到等弦，等弦的弧相等，等弦的弦心距相等。

（2）做等弧（等弦）的圆心角（圆周角），建立等角条件。

（3）连接等弧（等弦）端点，得到平行线。

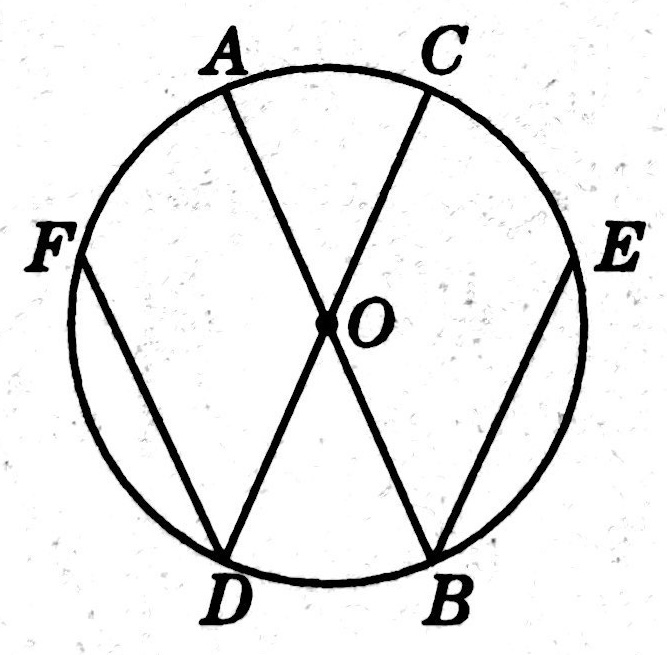
示例：如图 6 所示， \(AB,CD\) 是圆 \(O\) 的直径， \(DF,BE\) 是弦，且 \(DF=BE\) ，求证： \(\angle{D}=\angle{B}\) 。

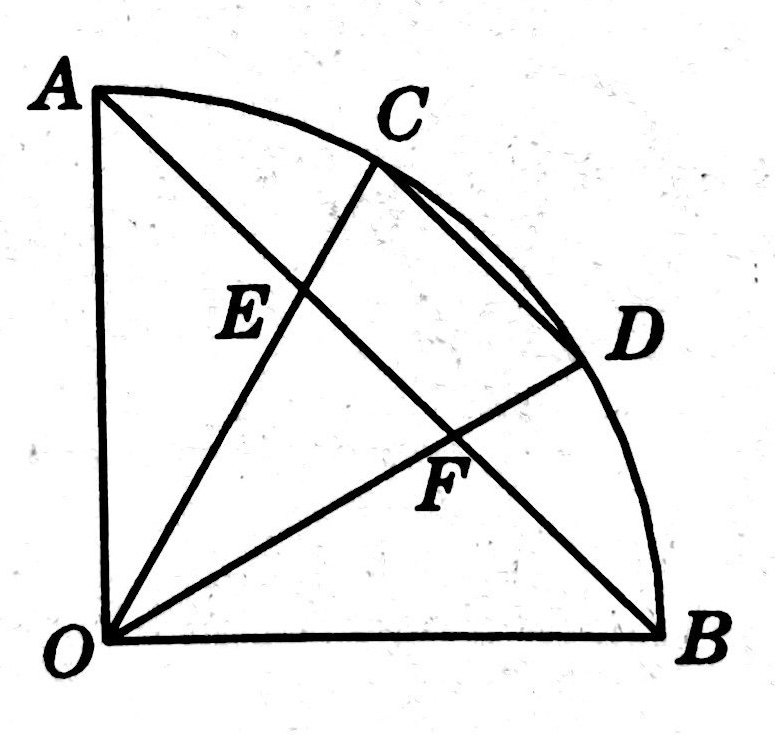
示例：如图 7 所示， \(\angle{AOB}=90^\circ\) ， \(C,D\) 是 \(\wideparen{AB}\) 的三等分点，连接 \(AB\) 分别交 \(OC,OD\) 于点 \(E,F\) 。求证 \(AE=BF=CD\) 。

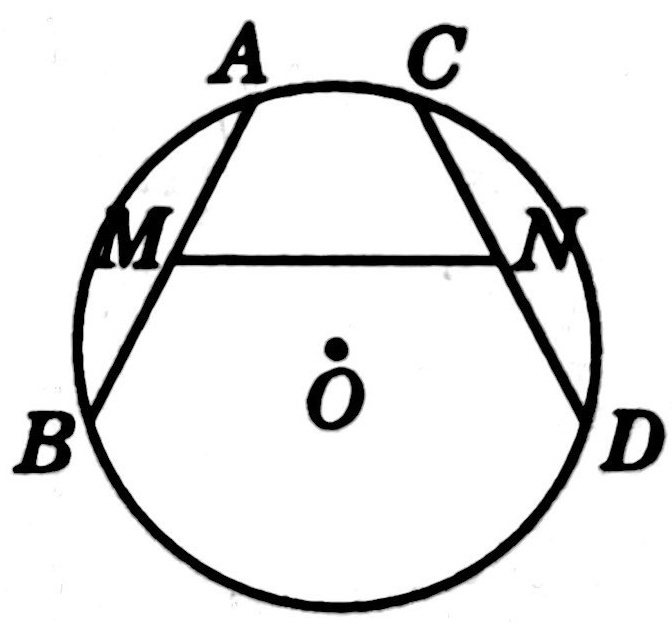
示例：如图 8 所示，在圆 \(O\) 中，弦 \(AB=CD\) ，点 \(M,N\) 分别是 \(AB\) 和 \(CD\) 的中点，连接 \(MN\) 。求证： \(\angle{AMN}=\angle{CNM}\) 。

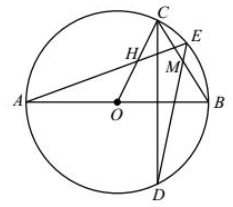
示例：如图 9 所示，弦 \(CD\) 垂直于圆 \(O\) 的直径 \(AB\) 于 \(L\) ，弦 \(AE\) 平分半径 \(OC\) 于 \(H\) ，\(DE\) 交 \(BC\) 于 \(M\) . 求证：\(M\) 为 \(BC\) 中点。

ypma0207_eg10_b

直径（参见图 10 ）

（1）做直径所对的圆周角，得到直角三角形。

（2）做和直径垂直的弦，得到垂直平分条件。

（3）配合另一弦中点，构造三角形中位线。

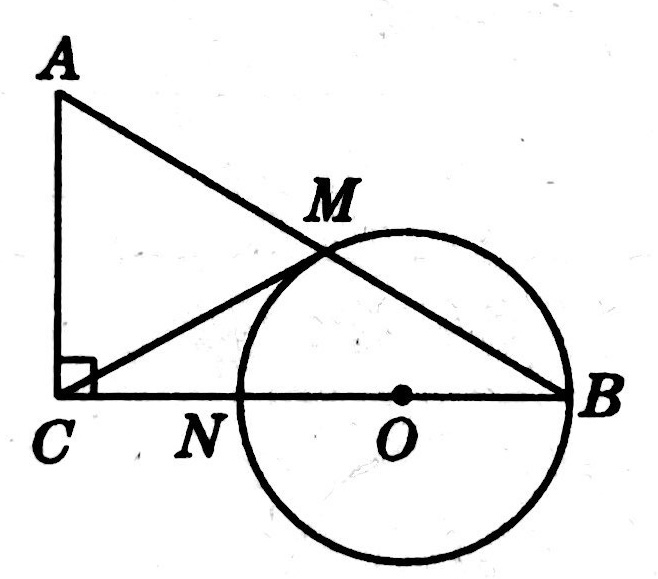
示例：如图 11 所示，在 \(\triangle{ABC}\) 中， \(\angle{ACB}=90^\circ\) ，以 \(BC\) 上一点 \(O\) 为圆心，以 \(OB\) 为半径的圆交 \(AB\) 于点 \(M\) ，交 \(BC\) 于点 \(N\) 。

（1）求证：\(AB\cdot BM=BC\cdot BN\) 。

（2）如果 \(CM\) 是圆 \(O\) 的切线， \(N\) 为 \(OC\) 的中点，当 \(AC=3\) 时，求 \(AB\) 的长。

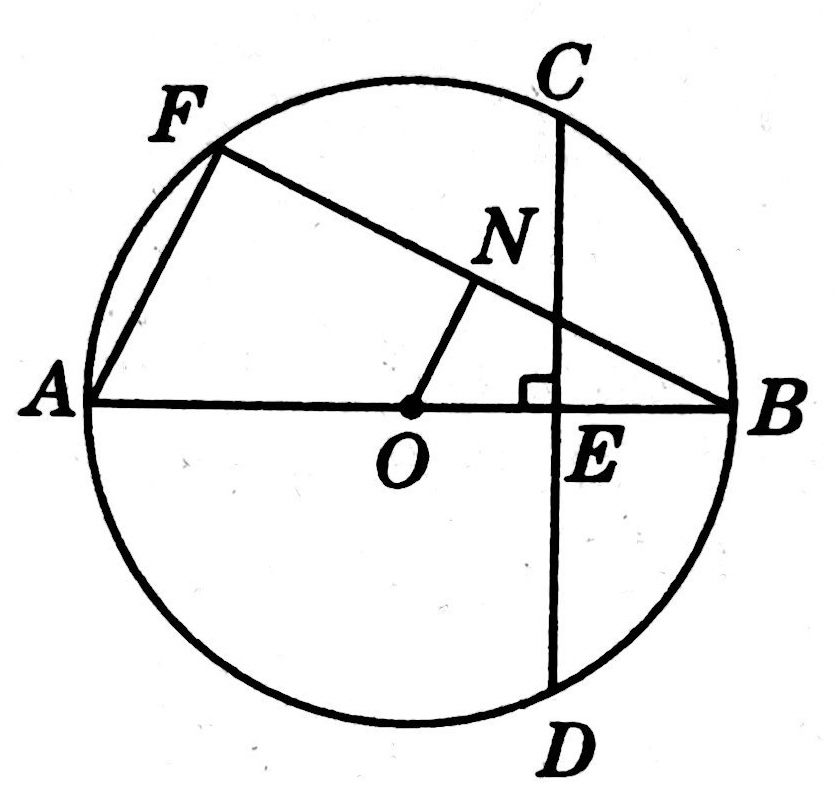
示例：如图 12 所示， \(AB\) 是圆 \(O\) 的直径， \(C\) 是圆 \(O\) 上一点，连接 \(AC\) ，过点 \(C\) 做 \(CD\perp AB\) 于点 \(D\) （\(AD<DB\)），点 \(E\) 是 \(DB\) 上任意一点（点 \(D,B\) 除外），直线 \(CE\) 交圆 \(O\) 于点 \(F\) ，连接 \(AF\) 交 \(CD\) 的延长线于点 \(G\) 。

（1）求证：\(AC^2=AG\cdot AF\) 。

（2）若点 \(E\) 是 \(AD\) 上（点 \(A\) 除外）上任意一点，上述结论是否仍然成立？若成立，请画出图形并给予证明；若不成立，请说明理由。

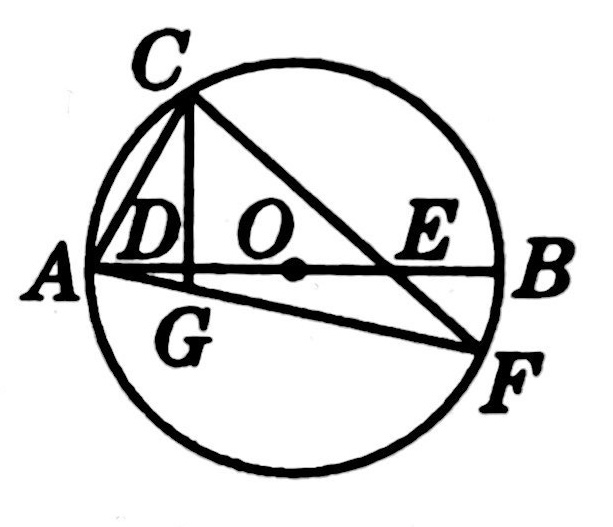
示例：如图 13 所示，\(AB\) 是圆 \(O\) 的直径，\(EF\) 是弦， \(AC\perp EF\) 于点 \(C\) ， \(BD\perp EF\) 于点 \(D\) 。求证 \(\angle{OCD}=\angle{ODC}\) 。

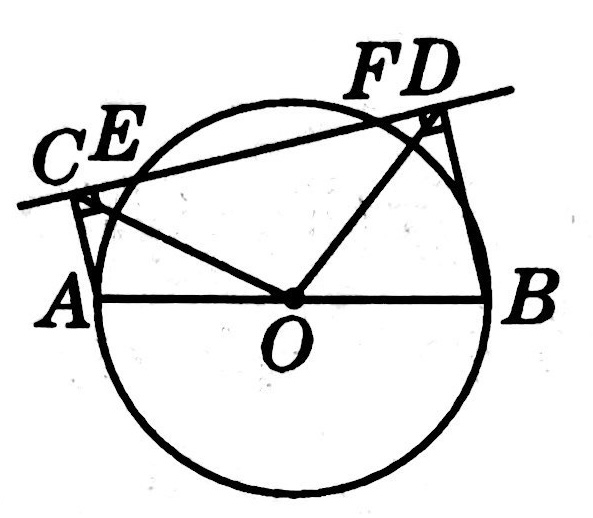
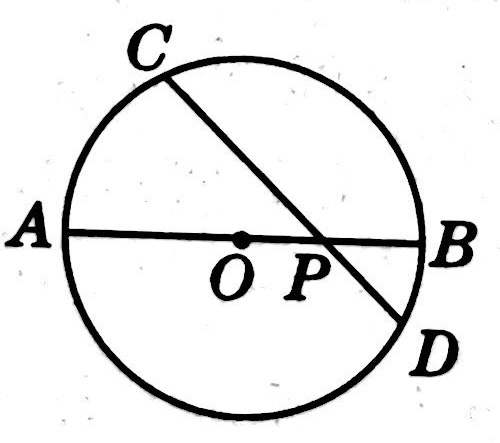
示例：如图 14 所示，圆 \(O\) 的直径 \(AB\) 与弦 \(CD\) 相交于点 \(P\) ，且 \(\angle{APC}=45^\circ\) ，若 \(PC^2+PD^2=8\) ，求圆 \(O\) 的半径。

四点共圆

（1）看到圆周四点，要想到四点共圆。

（2）四点共圆的等价条件是凸四边形对角互补。

（3）圆周角的外角等于内接四边形的对角。

（4）看见圆周角的邻角，要想到构建四点共圆。

（5）看见四个点有互补或等角，要想到利用四点共圆结论。

（6）一般地，看到诸点到一点等距，要想到诸点共圆。

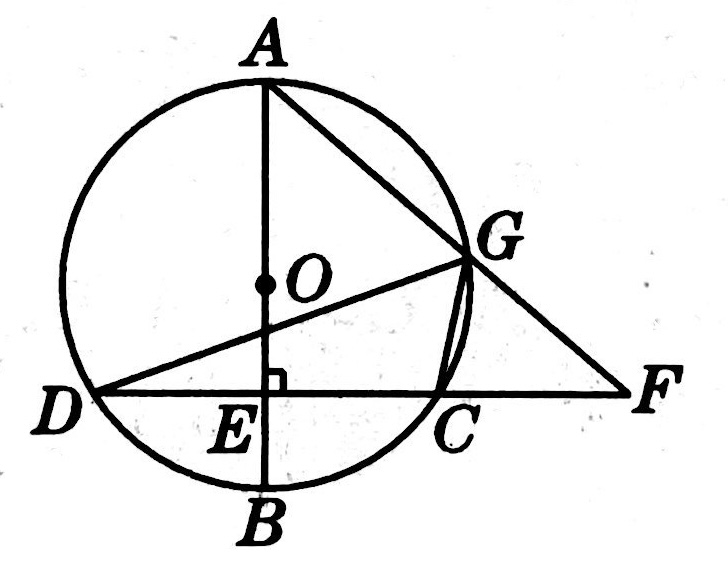
示例：如图 15 所示，\(AB\) 是圆 \(O\) 的直径，弦 \(CD\perp AB\) 于点 \(E\) ， \(G\) 是 \(\wideparen{AC}\) 上任意一点， \(AG,DC\) 的延长线交于点 \(F\) ，连接 \(DG,CG\) 。求证：\(\angle{FGC}=\angle{AGD}\) 。

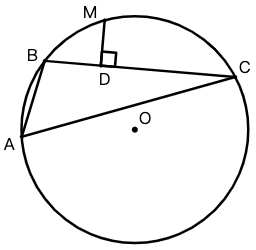
示例： 阿基米德折弦定理\(\bigstar\) 如图 16 所示， \(AB,BC\) 是圆 \(O\) 的两条弦， \(M\) 是 \(\wideparen{ABC}\) 的中点， \(MD\perp BC\) ，垂足为 \(D\) 。求证： \(AB+BD=CD\) 。

切线

（1）补齐切线和半径（直径）这一对垂直关系。

（2）配合割线作切线，得到比例中项，建立相似三角形。

（3）给切点欲证切线，连接半径证垂直。

（4）无切点欲证切线，做垂直证半径。

（5）两条切线取中央：连接切点，或者切线交点连接圆心。

示例：如图 17 所示， \(AD\) 是圆 \(O\) 的直径， \(AB\) 为圆 \(O\) 的弦， \(OP\perp AD\) ， \(OP\) 与 \(AB\) 的延长线交于点 \(P\) ，过点 \(B\) 的切线交 \(OP\) 于点 \(C\) 。

（1）求证：\(\angle{CBP}=\angle{D}\) 。

（2）若 \(OA=2,\ AB=1\) ，求线段 \(BP\) 的长。

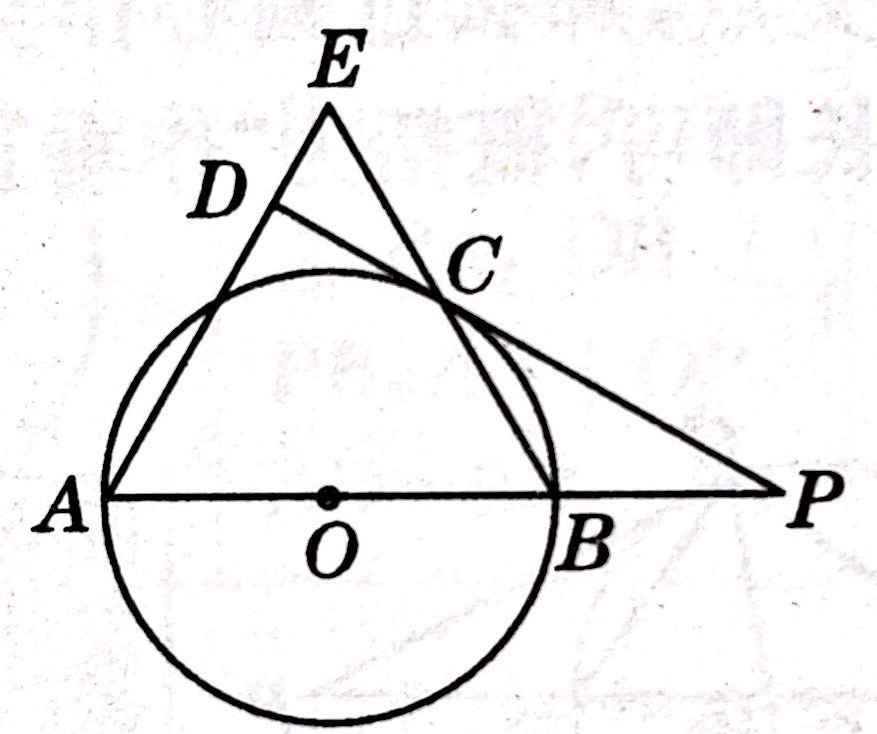
示例：如图 18 所示，\(AB\) 是圆 \(O\) 的直径，\(P\) 为 \(AB\) 延长线上一点， \(PD\) 切圆 \(O\) 于点 \(C\) ， \(BC\) 和 \(AD\) 的延长线相交于点 \(E\) ， \(AD\perp PD\) 。

（1）求证： \(AE=AB\) 。

（2）当 \(AB:BP\) 为何值时， \(\triangle{ABE}\) 为等边三角形？为什么？

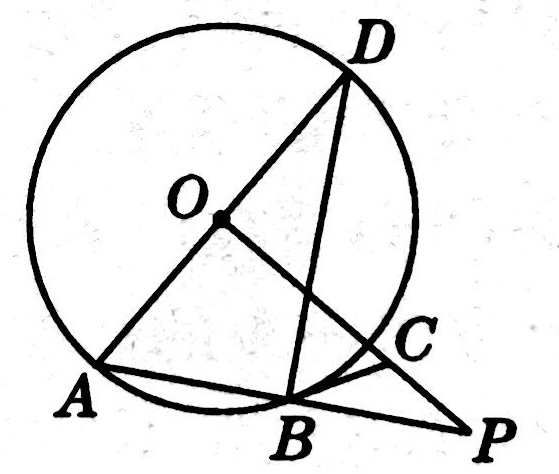
示例：如图 19 所示，在圆 \(O\) 中，点 \(C\) 是直径 \(AB\) 延长线上一点，过点 \(C\) 作圆 \(O\) 的切线，切点为 \(D\) ，连接 \(BD\) 。

（1）求证：\(\angle{A}=\angle{BDC}\) 。

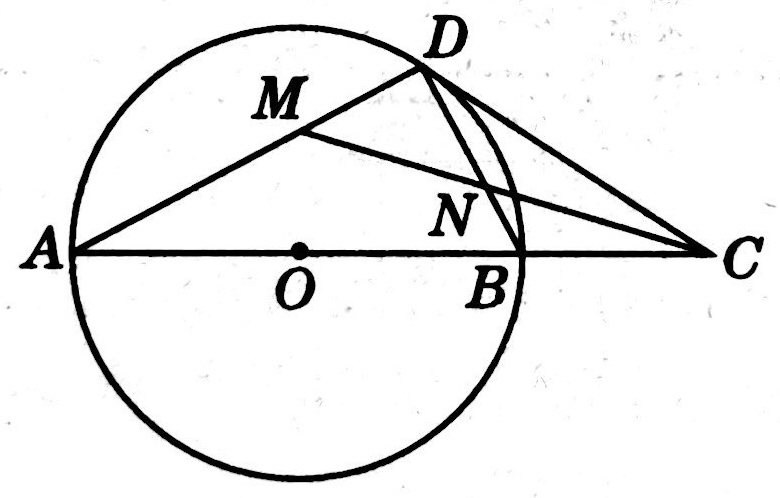
（2）若 \(CM\) 平分 \(\angle{ACD}\) ，且分别交 \(AD,BD\) 于点 \(M,N\) ，当 \(DM=1\) 时，求 \(MN\) 的长。

示例：如图 20 所示，圆 \(O\) 的直径为 \(AB\) ， \(D\) 和 \(E\) 分别是 \(\angle{ACB}\) 的平分线与圆 \(O\) 的交点， \(P\) 为 \(AB\) 延长线上一点，且 \(PC=PE\) 。求证：直线 \(PC\) 与圆 \(O\) 相切。

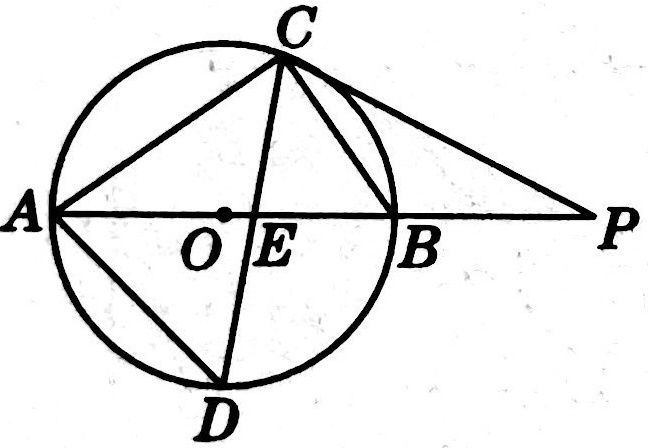
示例：如图 21 所示， \(AB\) 是圆 \(O\) 的直径， \(AC\) 是它的切线， \(CO\) 平分 \(\angle{ACD}\) 。求证： \(CD\) 是圆 \(O\) 的切线。

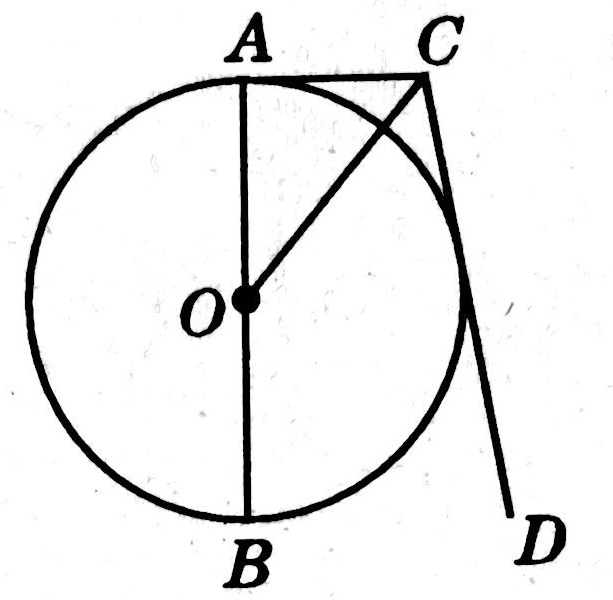
示例：如图 22 所示， \(PA\) 和 \(PB\) 分别与圆 \(O\) 相切于 \(A,B\) 两点，作直径 \(AC\) 并延长，交 \(PB\) 的延长线于点 \(D\) ，连接 \(OP,CB\) 。

（1）求证：\(OP\parallel CB\) 。

（2）若 \(PA=12\) ， \(DB:DC=2:1\) ，求圆 \(O\) 的半径。

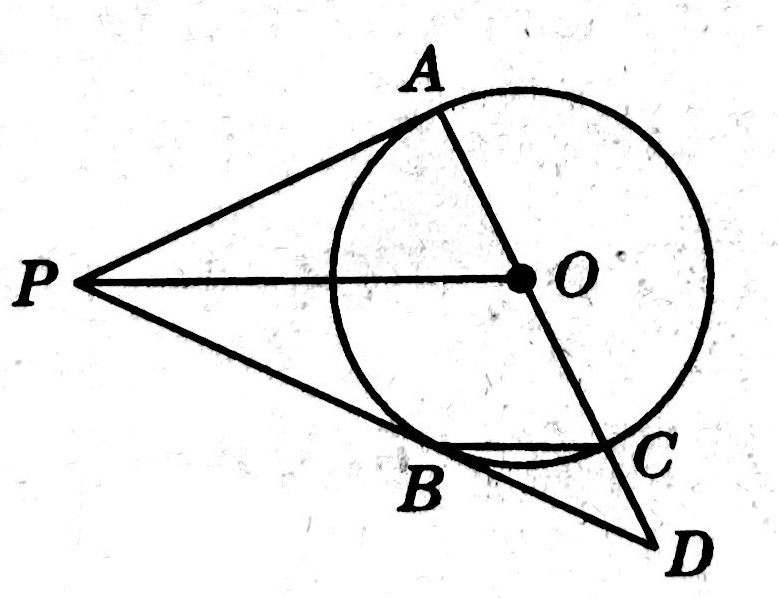
示例：如图 23 所示， \(PA\) 和 \(PB\) 分别与圆 \(O\) 相切于 \(A,B\) 两点， \(PQ\perp OQ\) 于点 \(Q\)， \(OQ\) 交 \(AB\) 于点 \(M\) 。求证： \(OA^2=OM\cdot OQ\) 。

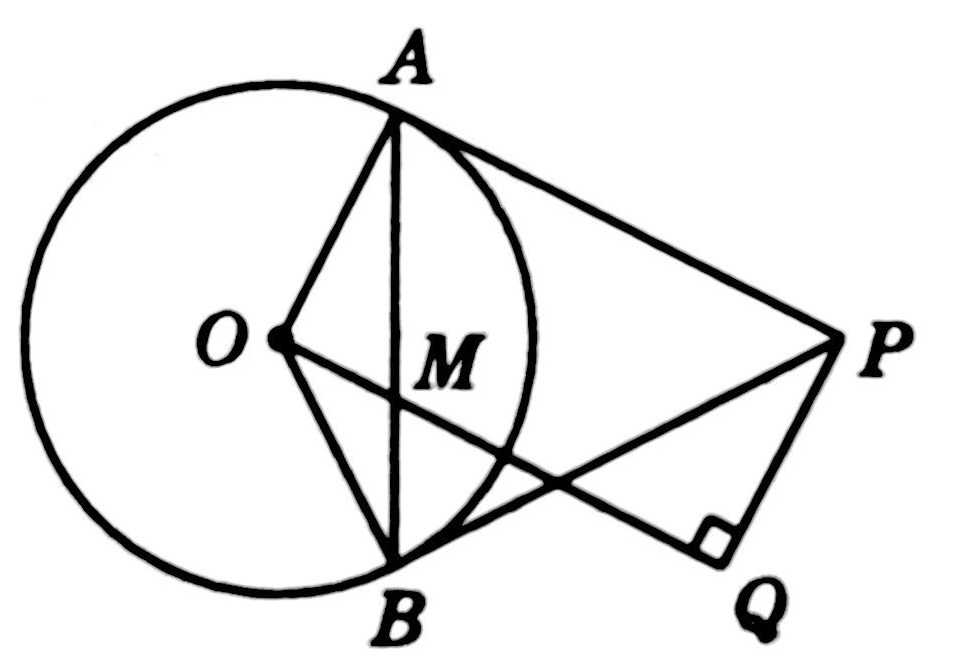
示例：如图 24 所示， \(AC,CD,BD\) 分别且圆 \(O\) 于点 \(A,E,B\) ，且 \(AC\parallel BD\) ，连接 \(OE\) ，求证：\(OE^2=AC\cdot BD\) 。

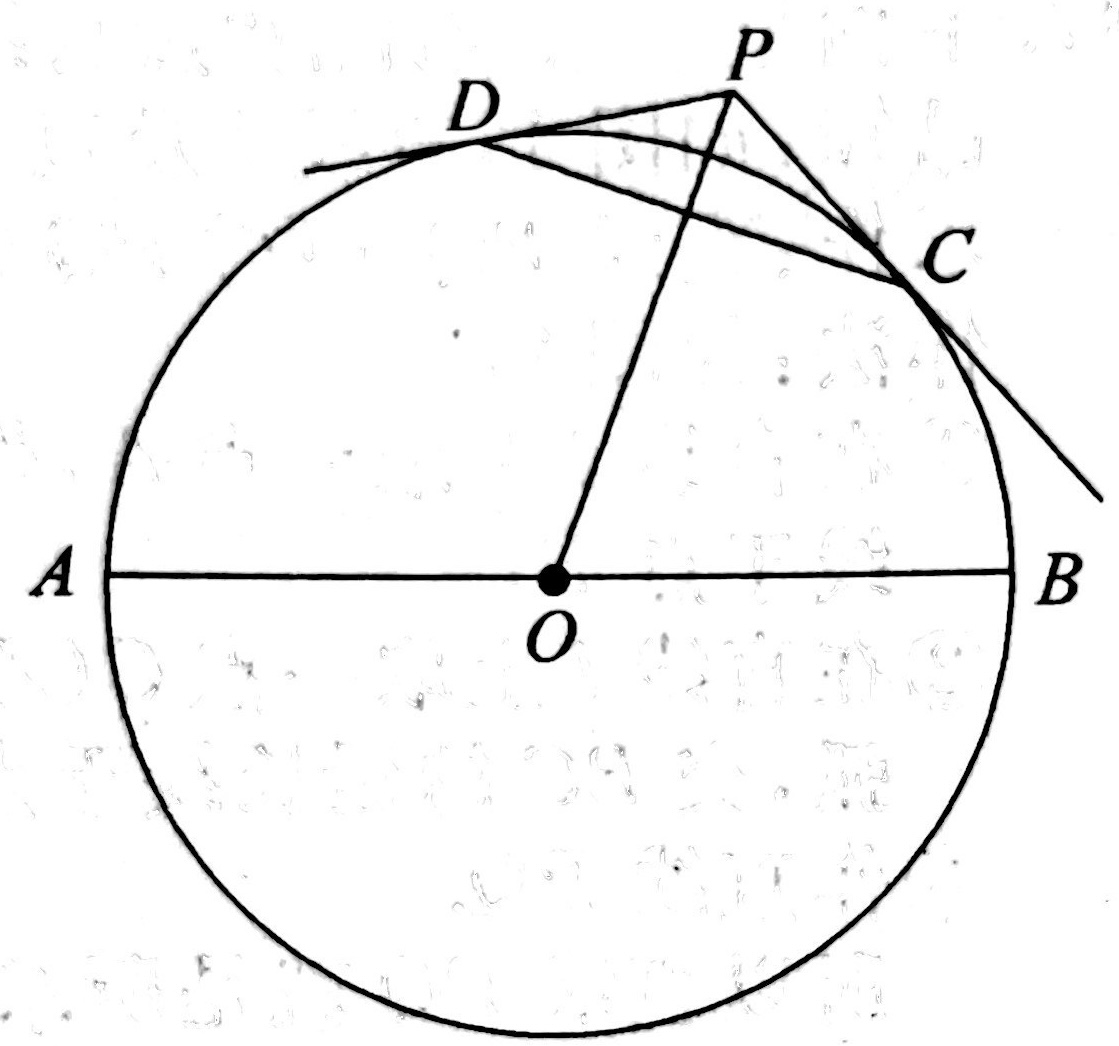
示例：如图 25 所示， \(AB\) 是圆 \(O\) 的直径，过圆 \(O\) 外一点 \(P\) 作圆 \(O\) 的两条切线 \(PC,PD\) ，切点分别为 \(C,D\) ，连接 \(OP,CD\) 。

（1）求证：\(OP\perp CD\) 。

（2）连接 \(AD,BC\) ，若 \(\angle{DAB}=50^\circ\) ，\(\angle{CBA}=70^\circ\) ，

\(OA=2\) ，求 \(OP\) 的长。

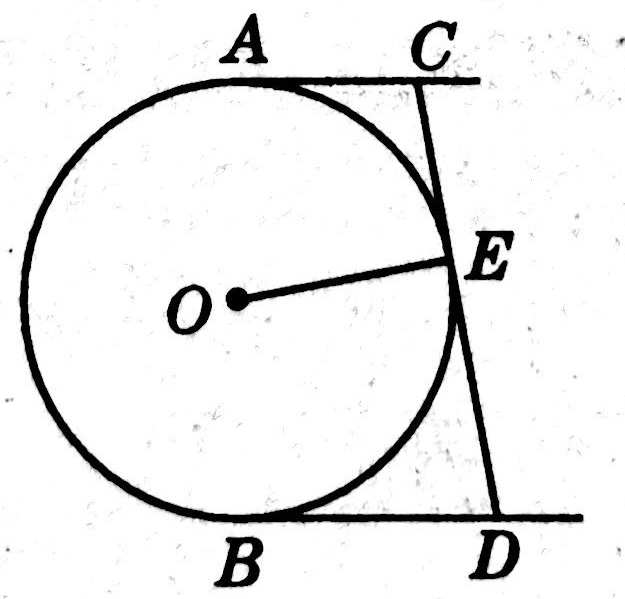
示例：如图 26 所示， \(AB\) 是圆 \(O\) 的一条弦， \(E\) 是 \(AB\) 的中点，过点 \(E\) 作 \(EC\perp OA\) 于点 \(C\) ，过点 \(B\) 作圆 \(O\) 的切线交 \(CE\) 的延长线于点 \(D\) 。

（1）求证：\(DB=DE\) 。

（2）若 \(AB=12\) ， \(DB=5\) ，求圆 \(O\) 的半径。

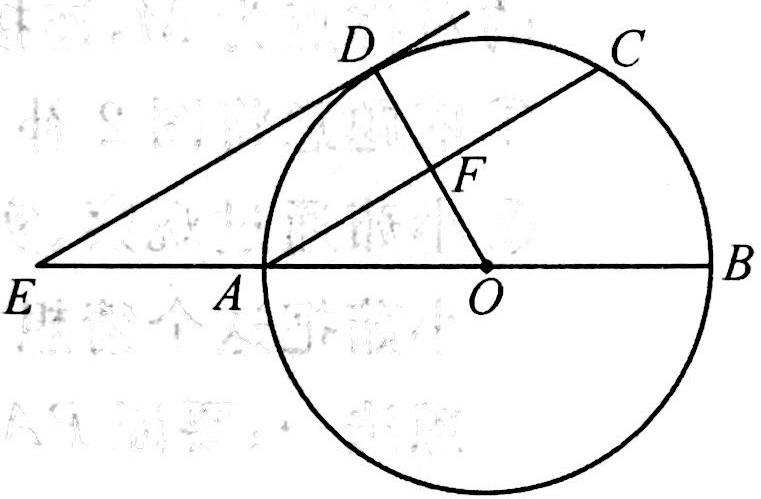
示例：如图 27 所示， \(AB\) 是圆 \(O\) 的直径， \(F\) 为弦 \(AC\) 的中点，连接 \(OF\) 并延长交 \(\wideparen{AC}\) 于点 \(D\) ，过点 \(D\) 作圆 \(O\) 的切线，交 \(BA\) 的延长线于点 \(E\) 。

（1）求证： \(AC\parallel DE\) 。

（2）连接 \(CD\) ，若 \(OA=AE=a\) ，写出求四边形 \(ACDE\) 面积的思路。

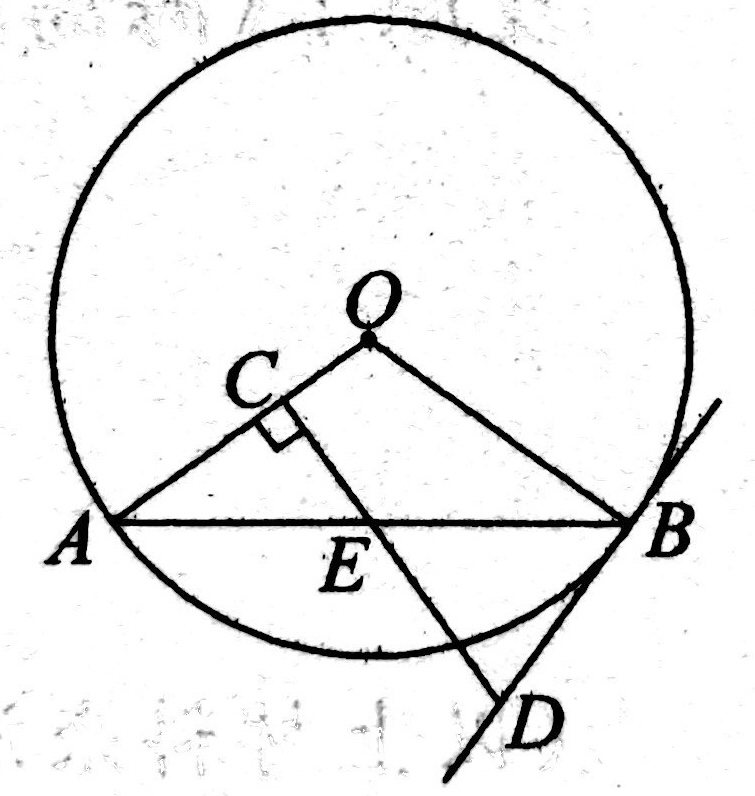
示例：如图 28 所示， \(AB\) 是圆 \(O\) 的直径，过点 \(B\) 作圆 \(O\) 的切线 \(BM\) ，交 \(AB\) 于点 \(F\) ，且 \(\wideparen{DA}=\wideparen{DC}\) ，连接 \(AC,AD\) ，延长 \(AD\) 交 \(BM\) 于点 \(E\) 。

（1）求证： \(\triangle{ACD}\) 是等边三角形。

（2）连接 \(OE\) ，若 \(DE=2\) ，求 \(OE\) 的长。

示例：如图 29 所示， \(AB\) 是 \(\bigodot O\) 的直径， \(C\) 为 \(BA\) 延长线上一点， \(CD\) 是 \(\bigodot O\) 的切线， \(D\) 为切点， \(OF\perp AD\) 于点 \(E\) ，交 \(CD\) 于点 \(F\) 。

[(1)] 求证：\(\angle{ADC}=\angle{AOF}\) ；
[(2)] 若 \(\sin C=\dfrac{1}{3},\ BD=8\) ，求 \(EF\) 的长。

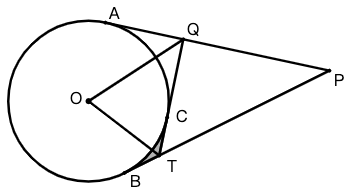
示例：如图，过 \(\odot O\) 外一点 \(P\) 作圆的两条切线 \(PA,PB\) ，切点为 \(A,B\) ，过 \(PA\) 上一点 \(Q\) 作切线 \(QC\) 交 \(PB\) 于 \(T\) ，切点为 \(C\) ，且 \(QC\perp PA\) ，若 \(BT=2\) ， \(\angle{TOQ}=75^\circ\) ，求阴影部分的面积。

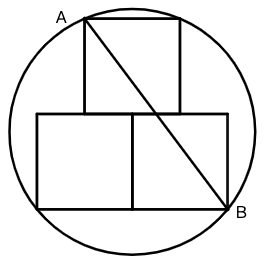
示例：如图是由三个大小相同的正方形组成的“品”字型轴对称图案，测得顶点 \(A,B\) 之间的距离为 \(5\) ，现用一个半径为 \(r\) 的圆形纸片将其完全覆盖，则 \(r\) 的最小值是多少？